分布式高空气球通信网络功率分配算法*

周文炯，尚建忠，王文政，吴庆睿

(1.成都工业学院 网络与通信工程学院，成都 611730；2.西安卫星测控中心，西安 710043；3.中国西南电子技术研究所，成都 610036)

0 引 言

高空气球是一类特殊的无人机，与普通无人机依靠燃料进行飞行和悬停不同，其升力主要由氦氢等气体提供，并可以通过绳索系留地面实现指定位置的长时间滞空，其能量消耗主要来自气球上携带的各种载荷[1]。高空气球ad hoc网络中普遍存在着相互干扰严重、节点能量受限等问题。具体来讲，某高空气球载荷功率过大不但会对其他高空气球的通信造成严重的干扰，还会影响自身作为网络节点的存活时间；另一方面，发射功率过小则可能导致链路的通信质量达不到要求。

针对上述问题，文献[2]在综合考虑功率分配、信道分配和路由选择等因素的基础上，提出了一种跨层的优化模型以提高网络的整体性能和生存时间；文献[3]从提高频谱利用效率的角度出发，讨论了分布式ad hoc网络中广泛使用的基于RTS/CTS的接入协议的最佳发射功率；文献[4]从优化ad hoc网络中任务配置的角度出发，探讨了如何降低整个网络的功耗；文献[5]从区分网络节点重要度的角度出发，研究了分层、多簇网络结构下的的分布式功率控制方法；文献[6]通过编队飞行技术，提升了ad hoc无人机网络的通信效率和质量；文献[7]利用ad hoc网络中节点的位置信息辅助决策，构建了一种合作博弈模型，提升了网络传输数据的能力；文献[8]利用深度学习理论，通过优化无人机的飞行轨迹，提出了一种适合无人机网络的功率分配算法，提升了整体网络容量。

文献[2-8]在分析分布式网络中的功率分配问题时，均是围绕节点通信速率优化、相互干扰的限制和节点电量受限这三个因素中的一个或两个展开的，而没有对三个因素进行通盘考虑。本文将综合考虑这三个因素，建立非合作博弈的模型，把节点的通信速率作为效用函数的基本收益项，保证节点的通信需求；通过在效用函数中引入干扰惩罚项，提升网络的整体信干噪比；利用将剩余电能引入效用函数，解决节点电量受限的问题。

1 系统模型

如图1所示，假设分布式高空气球网络中，所有高空气球作为通信节点采用自组织方式组网，且不设置任何中心控制节点，系统中存在N条单跳通信链路，对应于N个发射节点Si和N个接收节点Ri，其中i∈{1,2,3,…,N}。

图1 分布式高空气球网络示意图

所有节点共用信道，则接收机Ri处的信干噪比γi可以表示为

(1)

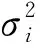
由香农公式可知，第i条通信链路对应的信道容量可以表示为

Ci=Blb(1+γi)。

(2)

式中：B为信道带宽。

2 功率分配算法

2.1 博弈模型

如果把所有发射机作为博弈的参与者，而把发射功率的调整作为博弈的策略，可以构建如下博弈模型：

(3)

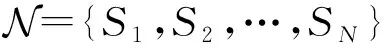
(4)

式中：p-i=[p1,p2,…,pi-1,pi+1,…,pN]表示除了发射机Si以外其他所有发射机的发射功率矢量。式(4)表示在这个博弈模型中，每个节点都设法使自己的系统效用函数最大化。

2.2 效用函数的设计和分析

从式(2)可知，当接收机处的噪声相对固定时，用户可以通过增大发射功率以获得更大的信噪比和传输速率。然而当发射机增加发射功率时，将会对其他用户造成更大的干扰。可以预见，如果网络中所有节点都期望通过增加发射功率来获得更好的性能，那么网络的整体性能反而将急剧恶化，为此需要在效用函数中增加关于干扰的惩罚项；同时伴随着功耗的增加，电池可用时间减少，因而可以考虑增加关于电能消耗的惩罚项。综上所述，整体的效用函数可以表示为

ui=Ci-Ii-Qi。

(5)

式中：Ci为发射机Si的收益项，即第i条通信链路对应的信道容量，可由式(2)获得；Ii为关于干扰的惩罚项；Qi为关于电能消耗的惩罚项。

设计干扰惩罚项Ii满足

(6)

式中：pi为发射机Si的发射功率，Gii、Gij分别为发射机Si到接收机Ri的信道增益和发射机Si到接收机Rj的信道增益，λ>0为干扰惩罚系数。在干扰惩罚项中，可以通过调节系数λ来调节网络的整体干扰水平，进而调节网络的通信质量。

对于电能消耗的惩罚，可以利用节点的剩余电能进行衡量。设计电能消耗惩罚项Qi满足[9]

(7)

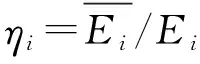
综合式(1)～(7)，可以得到完整的效用函数为

(8)

从式(8)可知，调节干扰惩罚系数λ的大小可以调节网络的整体干扰水平，λ增大时，发射机将更倾向于减少发射功率以获取更大的效用；反之当λ减小时，发射机则会倾向于增大发射功率。此外，当λ过大时，干扰惩罚将在本策略中起到绝对主导作用，用户的电量损耗对于发射功率的影响将被忽视；而当λ过小时，发射功率则会主要由用户的电池损耗决定，起不到控制整个网络干扰水平的作用。因而为兼顾考虑上述两方面因素，λ的选择应保证式(8)中的后两项为同一数量级，例如后文仿真中选取了两者均值相等。

2.3 纳什均衡的存在性和唯一性分析

纳什均衡是一种策略组合，使得每个网络节点的策略是对其他网络节点的最优反应。如果没有节点能够单方面偏离此状态以增加自身收益的话，那么这个策略组合就叫做纳什均衡[10]。在求解满足纳什均衡的发射功率前，需要证明模型中纳什均衡的存在性和唯一性。

(2)效用函数ui对于pi连续，并在pi上拟凹。

如果干扰方程I(p)同时满足以下三个条件则纳什均衡具有唯一性:

(1)正性,即I(p)>0;

(2)单调性;

(3)扩展性,即∀α>1，有αI(p)>I(αp)。

证明：

存在性：

(1)发射功率pi满足pimin≤pi≤pimax，即策略空间Pi=[pimin,pimax]。显然引理1的条件(1)是成立的。

(2)由于pi连续，效用函数ui显然也连续的，只需证明ui是凹函数即可。

ui对pi的一阶偏导数为

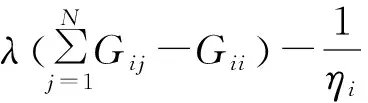
(9)

ui对pi的二阶偏导数为

(10)

显然引理1的条件(2)也是成立的，因而所提出模型具有纳什均衡点。

唯一性：

发射机i的最佳响应功率满足

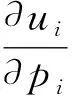
(11)

求解可得

(12)

实际发射功率还要满足pimin≤pi≤pimax，则

(13)

设p是博弈的纳什均衡，根据式(13)可知其干扰方程I(p)=p，其中I(p)=(I1(p),I2(p),…,IN(p))。

(1)正性：由于发射机Si的功率范围满足关系式pimin≤pi≤pimax，保证了I(p)>0。

(2)单调性：对于任意i∈N，设p>p′，则

显然I(p)是个单调减函数。

(3)扩展性：∀α>1，

αIi(p)-Ii(αp)=

(14)

对于式(14)，只需证明

(15)

由于实际的发射功率一定大于0，由式(12)可知，

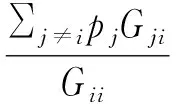
得证。

2.4 纳什均衡点的求解方法

Step1 设置初始时刻t=0时的系统发射功率矢量

p(0)=[p1(0),p2(0)…pN(0)],

并定义收敛精度ε>0；发射节点i(1≤i≤N)以功率pi(0)开始工作。

Step2 在时刻t=k，发射节点i，将p1=p1(k-1)，p2=p2(k-1),…,pi-1=pi-1(k-1)，pi+1=pi+1(k-1),…,pN=pN(k-1)代入式(13)，计算并更新当前发射功率pi(k)。

Step3 如果|p(k)-p(k-1)|<ε，则纳什均衡达成，否则返回Step 2继续迭代更新。

从上述迭代过程可以看出，实际应用中上述算法可以分布式进行，即每个发射机分别利用式(13)独立计算自身的发射功率，并在预设的公用控制信道上交互功率信息即可。而计算过程中，所需的各种状态信息可以通过以下方式获取：发射机Si到接收机Rj的信道增益Gij通过发射机Si侦听接收机Rj的导频信号获取；其他所有发射机到接收机Ri的干扰水平∑j≠ipjGji则可以通过接收机Ri感知获取；剩余电能百分比ηi是发射机Si的本地信息。因此本博弈算法可以分布式实现，具有可操作性。

3 仿真分析

如图2所示，假定10架高空气球构成的ad hoc网络位于100 km×100 km的空域之中，每架飞艇的滞空高度相同，其中5架作为发射节点(Tx)，另外5架作为接收节点(Rx)，所有网络节点共用信道。系统带宽为1.024 MHz，接收机噪声为10-7W，天线增益为30 dB。由于飞艇之间属于视距传播且多径效应较小，不失一般性可假设信道增益为d-2，其中d为发射机到接收机之间的距离。每个发射机携带的起始电池容量为60 kWh，最大发射功率为1 kW，并假定整个过程中所有节点均一直在传输数据，直到电池剩余能量小于20%为止。

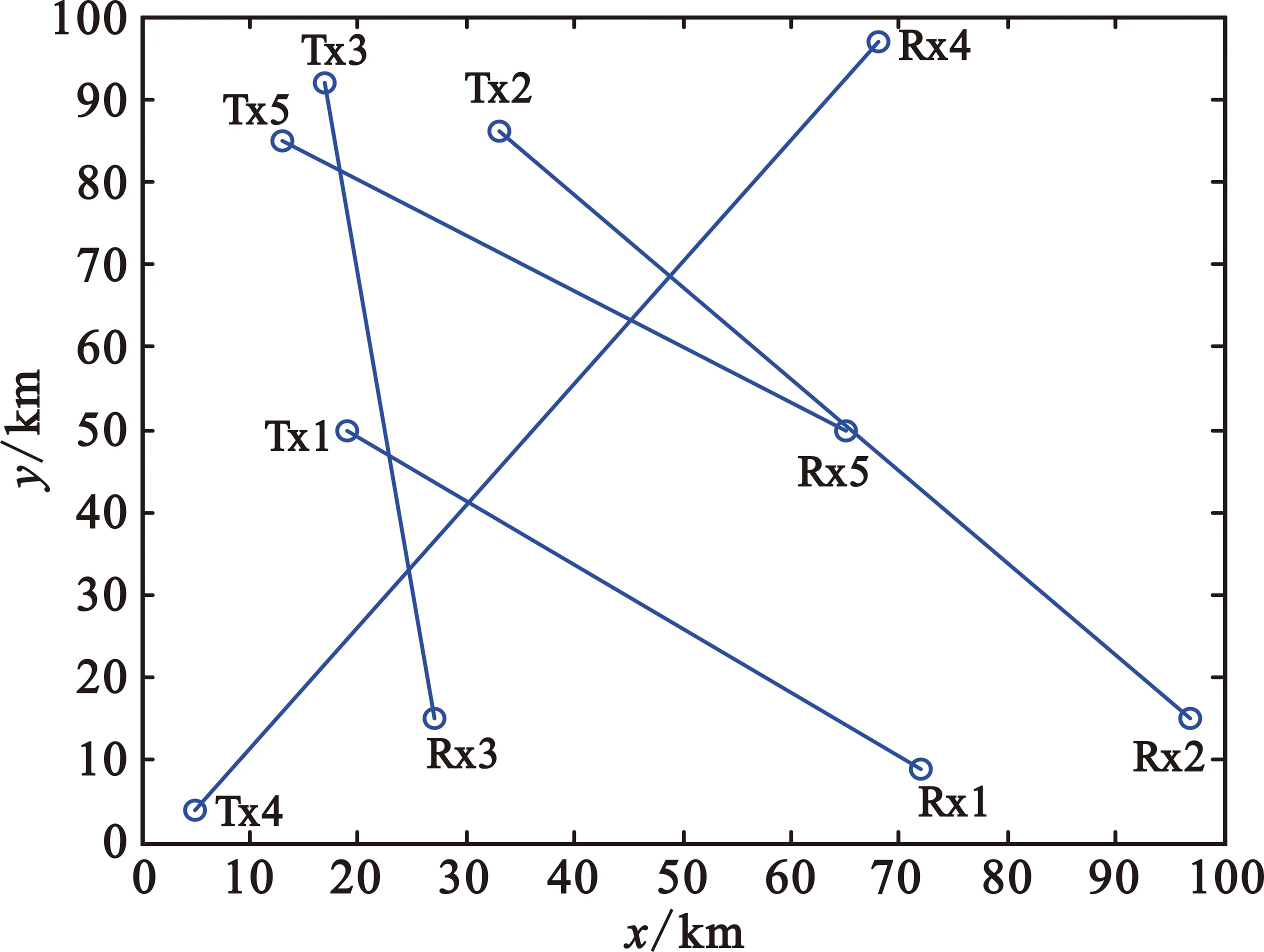
图2 高空气球位置分布图

图3给出了本算法中各节点发射功率的收敛情况。仿真中假定所有发射节点的起始功率为0，干扰惩罚系数λ=109，收敛精度ε=1 μW。仿真结果显示，本算法的收敛速度很快，只需经过9次迭代系统即可达到均衡状态，从而得到节点的最佳发射功率，证明了算法的高效性。

图3 功率算法的收敛情况

图4给出了ad hoc网络中各发射机功率随时间变化的趋势，整个过程可以分成3个阶段：

(1)所有发射机均在工作(阶段1,0～90 h)

本阶段初期，所有发射机的电池均处于满电量的状态，此时发射机将使用较大的发射功率以获取更高的传输速率；但随着时间的推移，发射机付出的能耗代价将随着电池的损耗逐步增大，因而各发射机功率都逐步降低。从图4可知，在t=0时，Tx5的发射功率达到了最大的848 W，而Tx4的发射功率只有410 W，这是因为Tx5距离其他四组通信的接收节点Rxi(i={1,2,3,4})的距离都较远，对它们的干扰较小，所以可以用较大的功率进行传输；而Tx4距离Rx3的距离非常近，只能通过减少功率避免对Rx3造成严重干扰。此外，在阶段1中，初始发射功率越大的节点其发射功率随时间减小的趋势也越明显，这是由于发射功率越大的节点其电池损耗得也越快，受到的能耗惩罚也越大。

图4 发射机的发射功率

(2)部分发射机退出工作(阶段2,90～112 h)

本阶段中，发射机将随着自身电量的耗尽逐个停止工作，其中在t=90 h和t=96 h时，Tx5和Tx3将依次耗尽电能停止工作，而剩下的三个节点则几乎同时在t=112 h时停止工作。从图4可以看到,当Tx5停止工作时，Tx1、Tx2、Tx3和Tx4的发射功率同时增大；而当Tx3停止工作时，Tx1、Tx2和Tx4的发射功率也有明显提升。这是因为每减少一个用户时，继续工作的发射机对其余工作中的接收机的总干扰将会减少，受到的干扰惩罚也会降低，促使了该发射机使用更大的功率工作。

(3)所有发射机电量耗尽(阶段3,112 h之后)

本阶段所有发射机已经耗尽能量，超过最大生存时间，ad hoc网络失效。

图5给出了ad hoc网络中各发射机剩余电能随时间变化的趋势，各条曲线的斜率代表着各发射机电池损耗的速度。随着时间的推移，各发射机剩余电能逐步减少，且大多数情况下随着剩余电能的变小，电池损耗的速度也在放缓，只有在有发射机退出工作，剩余发射机增大功率的瞬间，电池损耗会突然加快。

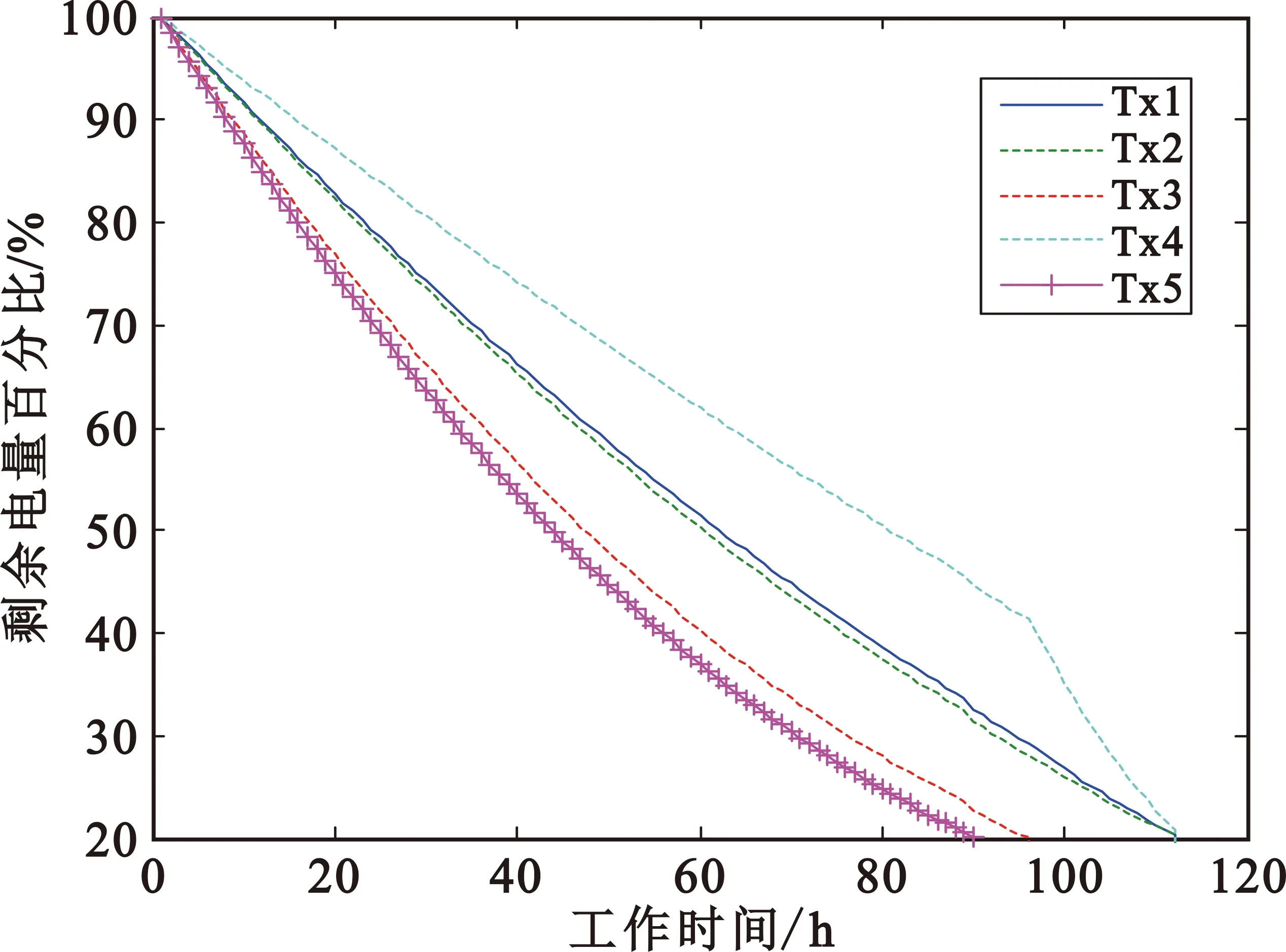
图5 发射机剩余电量百分比

图6则给出了ad hoc网络中5条链路的容量随时间变化的趋势。在所有发射机均处在工作状态的0～90 h内，随着时间的推移，链路3和5的容量会逐步减少；而链路1、2、4的容量却逐步增大。对比图4可以看出：Tx3和Tx5是发射功率减少最快的两个发射机，发射功率的快速减小将使得这两条信道上的信干噪比(Signal-to-Interference plus Noise Ratio,SINR)也减少，从而导致容量的变小；另一方面，在链路1、2、4中，Tx1、Tx2和Tx4的发射功率减小缓慢，但由Tx3和Tx5造成的干扰却迅速减小，使得这三条链路上的SINR反而会随着时间增大，从而导致了这三条链路的容量不降反增。而在部分发射机停止工作的90～112 h内，链路的容量变化则比较复杂，可以看出当有发射机退出网络时，其余链路的容量可能突然增大(比如90 h时的Tx1和Tx2)或减少(比如96 h时的Tx2)。前者主要由于90 h时Tx5退出，使得Rx1和Rx2受到的干扰减少；而后者则是96 h时，虽然Tx3退出工作，但因为Tx4功率增加较大，使得Rx2受到的干扰反而增加。

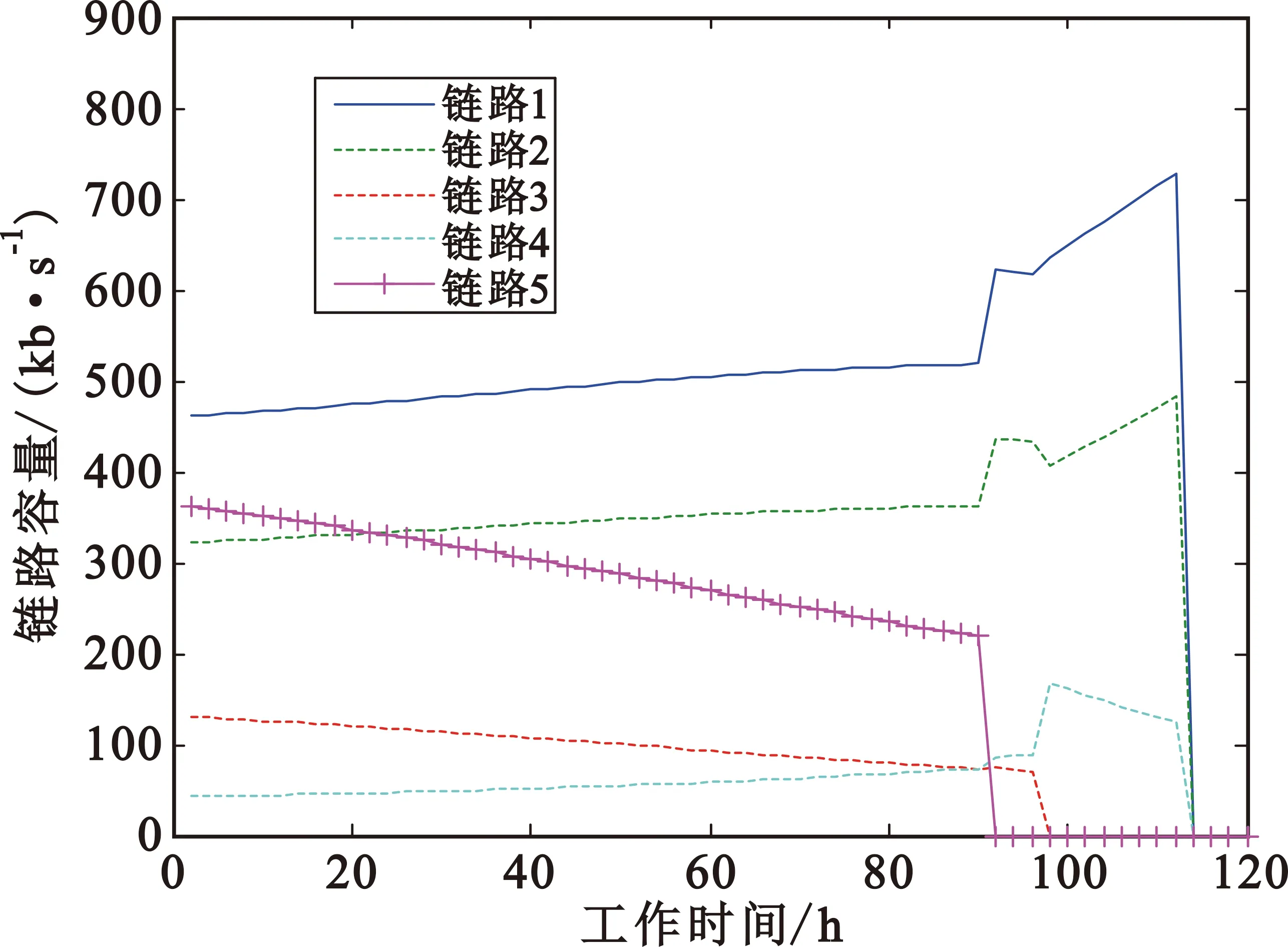
图6 各条链路容量

图7给出了采用本文算法、采用RTS/CTS算法[3]和采用HATA算法[4]时，各发射机生存时间的比较。图7显示，所有发射机在采用本文算法时生存时间均为最长，各节点的平均生存时间分别为采用 RTS/CTS算法的2倍、采用HATA算法的1.6倍。

图7 各发射机生存时长对比

图8给出了各条链路以最大传输速度进行传输时，在整个链路存活期间可传输的数据量。图8的结果表明，采用本算法时，每条链路的数据量均达到了RTS/CTS算法的3倍以上，5条链路的数据总量则达到了RTS/CTS算法的3.5倍；而同HATA算法的对比中，链路1、2、5的数据量达到了HATA算法的2倍以上，链路3的数据量高出HATA算法6.1%，只有链路4的数据量比HATA算法低3.4%,5条链路的总数据量则达到了HATA算法的1.81倍。

图8 各链路的数据量对比

4 结 论

本文研究了高空气球通信网络中节点通信速率、节点间相互干扰和节点电量三者之间的关系，设计了基于博弈论的分布式ad hoc网络功率分配算法，通过在效用函数中设置干扰惩罚项避免了节点间的恶性竞争，降低了网络的整体干扰水平，提高了各通信链路的吞吐量；通过在效用函数中设置电能消耗的惩罚项延长了各节点的存活时间，增加了网络的吞吐量。所提出博弈模型存在纳什均衡，且均衡点唯一，算法具有快速的收敛性。仿真结果表明，所提出算法的节点生存时间和传输的数据总量比其他算法均具有较为明显的优势。