基于主成分分析法与人工神经网络耦合模型的水质评价

朱永军， 吴 琼， 湛忠宇

(江苏省水文水资源勘测局南京分局， 江苏 南京 210008)

1 研究背景

合理对水体质量进行分析评价能够为水质治理提供科学的方向，同时也是区域改善水环境的基础，目前，存在多种对水质进行评价的方法，传统的单因子评价法[1]以最差的水质指标所处等级作为评价结果，极易受到极端指标的影响，不能反映出真实情况；灰色理论[2]，模糊数学法[3]、层次分析法[4]在确定指标权重时往往忽略了因子之间的相互影响且主观性较强；传统主成分分析法[5-6]采用标准差对数据进行标准化，使得同类指标之间的方差为零，消除了指标之间的差异；传统的神经网络法[7]将所有的监测指标作为输入数据，增加了模型复杂程度，效率低下。本文针对水质评价中评价指标权重难以合理确定，评价模型过于复杂、评价结果不合理等问题，依据南京市六合区的水质监测资料，提出主成分分析与神经网络相结合的方法，以期为合理进行水质评价提供一种新思路。

2 研究方法

2.1 改进的主成分分析

主成分分析[8]的主要思想是利用正交变换对原始数据进行降维处理，找出一组线性无关的主成分，以此代表原始数据的大部分信息，一般分为以下几个步骤。

1)对原始数据进行标准化处理，消除量纲不同带来的影响。本文采用均值化方法对原始数据进行标准化，在保留同类变量间的差异信息的同时，消除量纲的干扰，计算公式为

ZXij=Xij/MeanXi

(1)

式中，ZXij为第i个指标的第j个数值标准化后的结果；Xij为第i个指标的第j个数据的原始值，MeanXi为第i个样本的平均值。

由于水质指标中大部分为逆向指标，正向指标即数值越大表明水质越好的指标，采用下式进行标准化处理：

ZXij=(MaxXi-Xij)/Mean(MaxXi-Xij)

(2)

式中，MaxXi为第i个指标的最大值。

2)计算标准化后ZXij的相关系数矩阵R；

3)计算R的特征值λi和特征向量并将特征向量按照从大到小进行排列；

4)计算累计方差贡献率确定主成分个数。以前n个特征值的和占总特征值的百分比作为累计方差贡献K，一般取K≥85%；

5)计算主成分Fi的值及主成分综合得分,得分越高说明水质越差，其中

(3)

2.2 BP人工神经网络

BP神经网络[9-10]是一种多层前馈神经网络，依靠大量神经元的联系，形成一个非线性的动态系统。BP神经网络一般由输入层、隐含层和输出层三部分组成，其中隐含层可以有一个或多个(图1)。在网络的运行过程中输入的数据由前向后传播，每一层的神经元输出结果只对与其直接相连的下一层神经元有影响，同一层的神经元直接互不连接，互不干扰。

图1 BP神经网络结构图

构建BP神经网络一般有如下几个步骤：

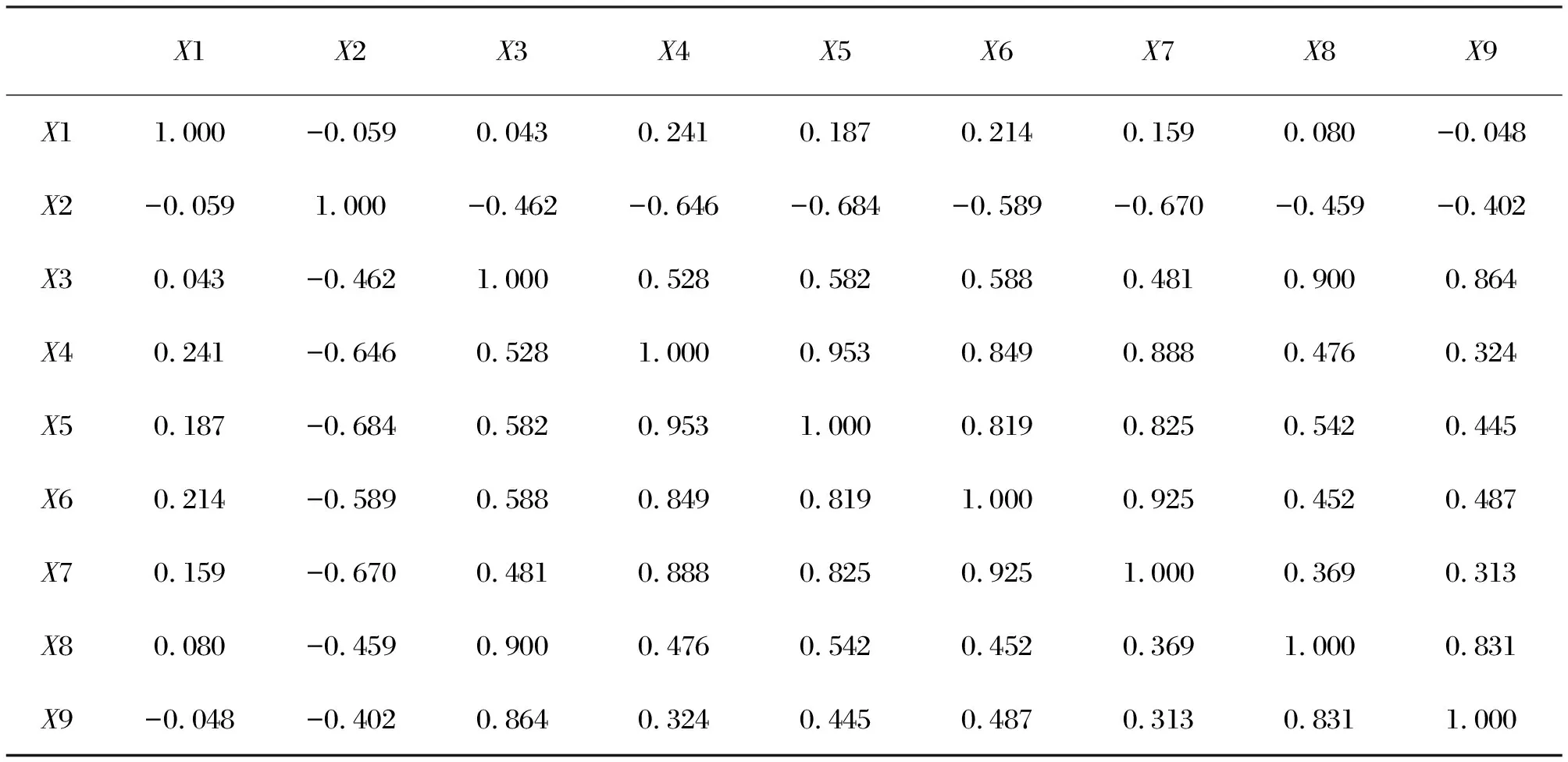
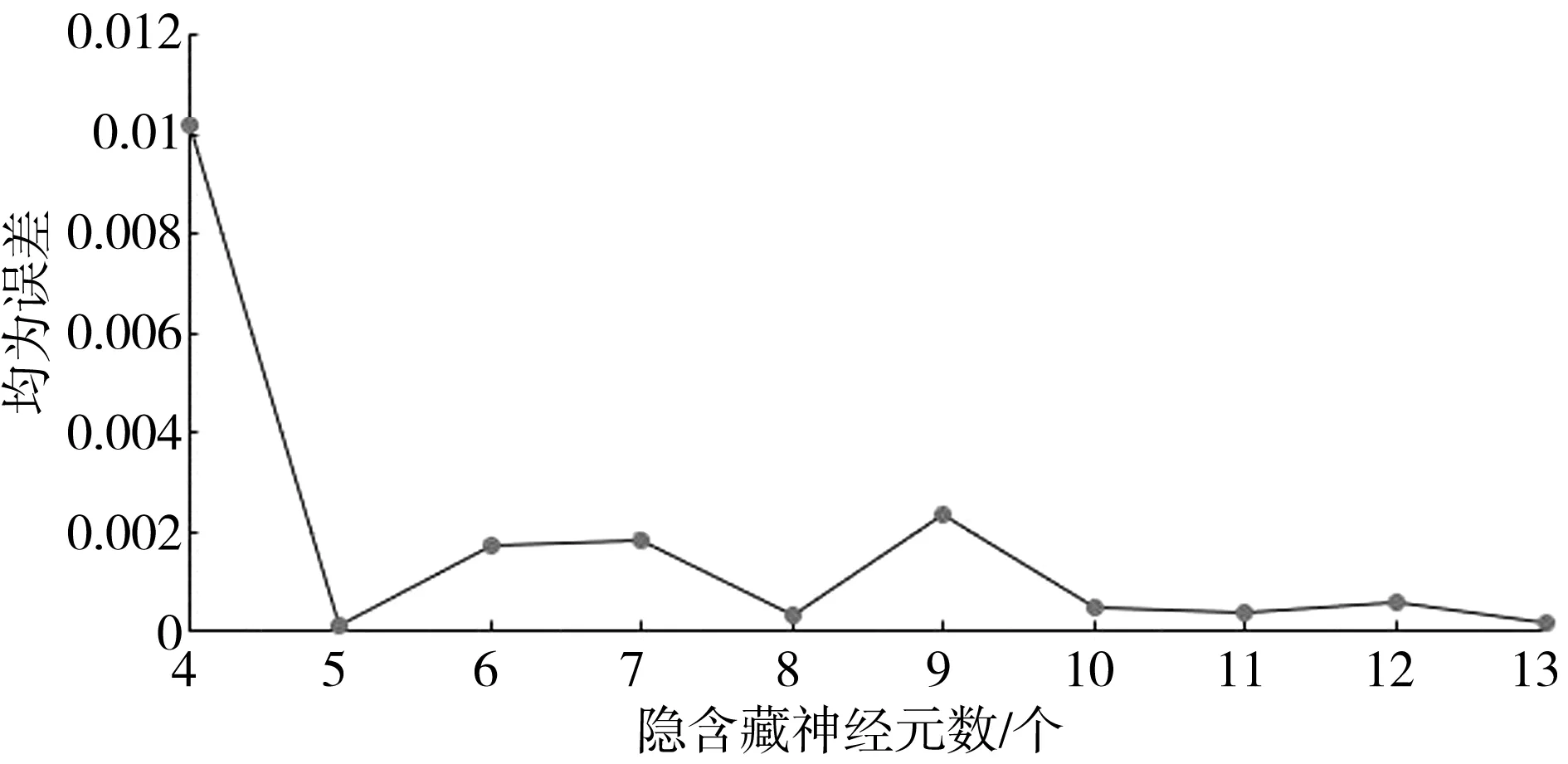
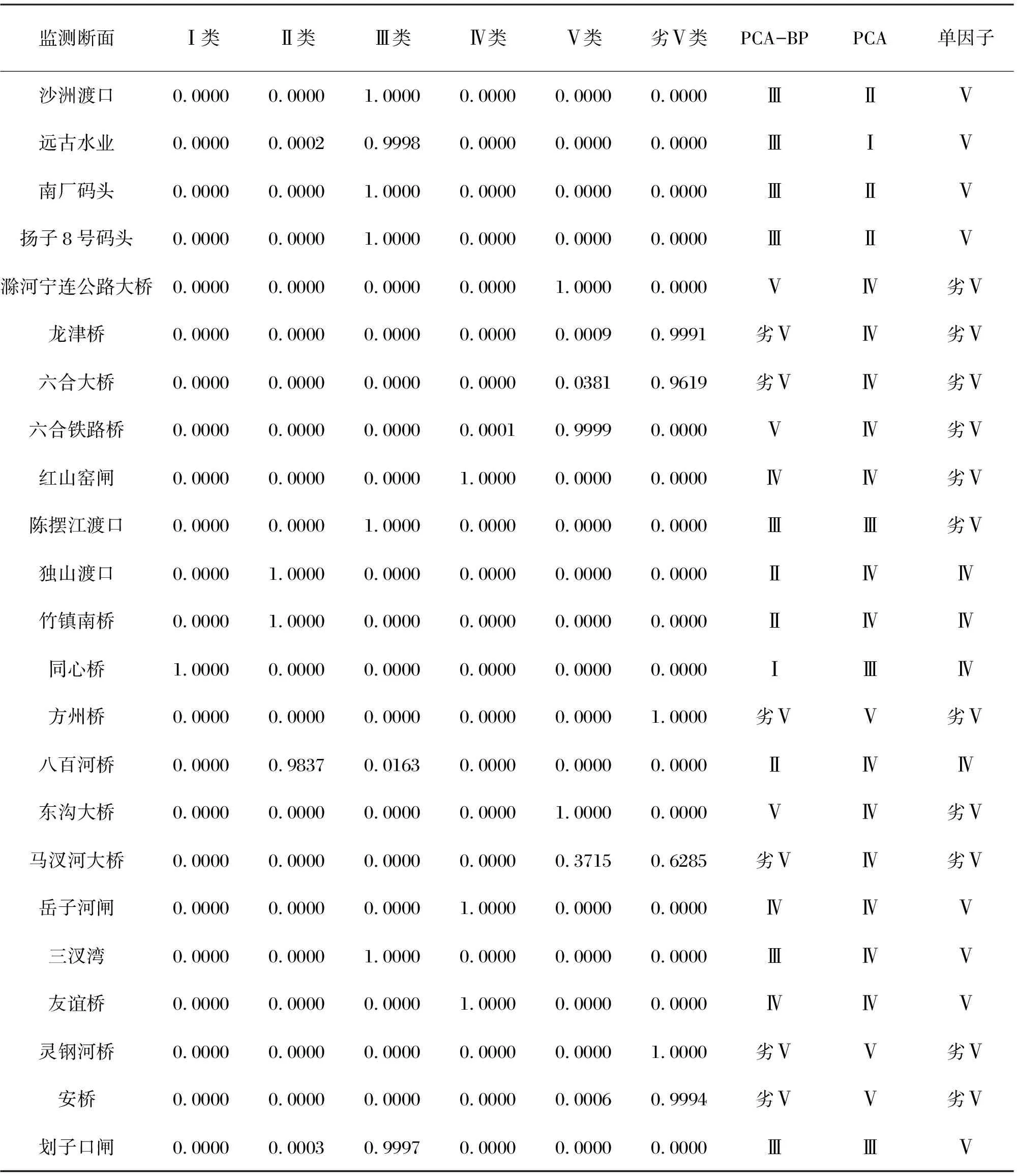
1)对输入数据集{Xi}(1

3)构建神经网络，设定各层传递函数、最大允许步长、模型精度等；

4)当模型满足设定精度时，保存模型，进行水质评价。

3 计算与分析

3.1 主成分分析

六合区位于南京市北部，长江左岸，是国家重要的现代工业基地，滁河由西到东贯穿境内。本文选取2019年南京市六合区23个监测断面年平均水质数据进行实例分析。由于监测数据中金属离子及石油类、挥发酚等按《地表水质量评价标准》(GB3838—2002)评价均为Ⅰ类，故在主成分分析中不对其进行分析。筛选后主要的评价因子有pH(X1)、DO(X2)、NH3-N(X3)、CODMn(X4)、COD5(X5)、F(X6)、COD(X7)、TP(X8)、TN(X9)共9类。

(1)对数据进行均值化处理，计算相关系数矩阵，由表1可知大部分监测指标相关系数均大于0.3，说明各指标之间存在信息的重叠，因此适用主成分分析对原始数据进行降维处理。

表1 相关系数矩阵

(2)计算特征值和主成分贡献率，得到每个主成分所对应的解释方差、特征值和累计方差贡献率，由表2可知前3个主成分累计反映了原始参数信息的88.469%，可将原来11个影响指标减少为3个，进而大大降低因子的维数。

表2 特征值及累计方差贡献率

由主成分荷载矩阵可以看出，F1中DO、CODMn、COD5、F、COD对其影响程度较大，可认为F1在一定程度上表示了水体的有机污染；F2中NH3-N、TP、TN对其影响程度较大，可认为F2在一定程度上表示了水体的无机污染；F3中pH对其影响程度较大，故可认为F3在一定程度上表示了水体的酸碱性。

(3)根据主成分荷载矩阵计算各主成分的对应指标的得分系数，由此计算F1、F2、F3的值并根据公式(4)计算综合得分F，主成分得分越大说明水质越差，如表4所示。其中按照《地表水环境质量标准》各类水质的标准值计算得到Ⅰ类水质主成分综合得分为的-2.891、II类为-2.008、III类为-0.706、IV类为1.788、V类3.817。

表3 主成分荷载矩阵

F=0.108ZX1-0.178ZX2+0.360ZX3+0.211ZX4+0.229ZX5+0.224ZX6+0.184ZX7+0.426ZX8+0.486ZX9

(4)

由表4可知仅有3个断面的评价结果与单因子评价法保持了相同，这是因为这些断面中大多数水质指标都处单因子评价法的评价等级。其余20个断面评价结果提升了1～3个等级，这是因为这些断面水质指标仅有少数处于单因子评价法的评价等级。主成分分析法的综合考虑了所有评价指标，避免了某一评价因子将其他因子的信息完全覆盖，让一些处于“劣势”的指标得到了反映，评价结果与单因子评价法在整体上的趋势是相同的，因此具有一定的合理性。但是可能存在过于乐观的评价结果，比如远古水业断面，除DO、COD5为Ⅰ类外，其余各指标均在Ⅲ类和Ⅳ类之间，因此主成分分析法将其评价为Ⅰ类过于乐观。

表4 主成分分析评价结果

(5)通过主成分分析对原本的9个评价指标进行降维，得出的3个主成分能够反映原指标88.469%的信息，大大简化了信息处理的维度；由主成分的综合表达式可以看出NH3-N、TP、TN相比其他指标在权重方面占有绝对的优势，因此认为NH3-N、TP、TN是六合区的主要污染物，这与南京市水资源公报里的分析结果同样是吻合的，因此后续搭建神经网络模型，以此3项指标作为模型的输入数据。

3.2 构建BP神经网络模型

(1)生成样本数据

样本的数量和差异性对神经网络的模拟精度有重要影响，为获得足够多的样本，将各项指标测定国标法中最低检出浓度作为Ⅰ类下限值，结合《地表水环境质量标准》(GB3838—2002)可以得到各级水质的上下限值，在各类水质等级之间进行随机插值(比如当N、TP、TN分别处于(0.15，0.5]、(0.02，0.1]、(0.2，0.5]之间时，该水体水质肯定属于Ⅱ类)，考虑到研究区域水质多为劣Ⅴ类，因此共设置六个水质等级(Ⅰ～劣Ⅴ类)，每两级之间随机插值生成450个样本，共2 700个样本。

表5 地表水环境质量标准各项指标限值 单位：mg/L

(2)样本数据预处理

在MATLAB中将样本矩阵P的每一个元素归一化到[-1，1]，样本集作为输入样本时是一个5×2 700的矩阵，其中每一列代表一个样本，共2 700个样本。

(3)确定目标矩阵

输出层共有6种水质类别，因此输出层选用6个神经元。用6×1的矩阵表示每个输出类别，其中(1,0,0,0,0,0)T表示Ⅰ类水质、(0,1,0,0,0,0)T表示Ⅱ类水质、(0,0,1,0,0,0)T表示Ⅲ类水质、(0,0,0,1,0,0)T表示Ⅳ类水质、(0,0,0,0,1,0)T表示Ⅴ类水质、(0,0,0,0,0,1)T表示劣Ⅴ类水质。每一个输入样本对应一个输出矩阵，因此目标集T为一个3×2 700的矩阵。

(4)创建神经网络

在MATLAB中输入样本集[P,T]，将样本中的75%用于训练网络，10%用于验证，15%用于测试；隐含层神经元个数按照经验公式取值在[4,13]之间，先选取4个神经元进行训练，然后依次增加神经元的个数直到15，依据神经元个数和均方误差(图2)及神经元个数和训练步长(图3)的关系，确定隐含层神经元个数为11。

图2 隐含层神经元数与均方误差的关系

图3 隐含层神经元数与步长的关系

此时模型运行了76步，在第70步时达到了最佳表现，如图4所示。通过输入层、隐含层、输出层神经元个数的确定，最终的神经网络采用3-11-6的3层网络结构。

图4 n=11时训练表现

(5)进行水质评价

由表6可以看出，PCA-BP神经网络法的评价结果与单因子评价法和主成分分析法的评价结果在整体趋势上同样是一致的。相比单因子评价法，龙津桥、六合大桥、方州桥、马汊河大桥、灵钢河桥、安桥6个断面神经网络的评价结果与其完全一致。远古水业、南厂码头、扬子8号码头等断面评价结果上升了2个等级；滁河宁连公路大桥、六合铁路桥、友谊桥等断面1个等级。劣Ⅴ类断面占比由47.8%下降为26.1%；Ⅴ类断面占比由34.8%下降为13.0%；Ⅳ类断面减少100%；新增Ⅲ类及Ⅲ类以上断面7个。与主成分分析法相比，陈摆江渡口、岳子河闸、划子口闸断面与其评价结果完全一致，对于远古水业断面，PCA-BP神经网络法对上文的主成分分析法的结果进行了一定程度上的“纠正”，避免了评价结果的过分乐观。

表6 神经网络评价结果

4 结 论

本文针对六合区23个断面水质监测数据，首先利用改进的主成分分析法对各断面水质进行评价，并由此确定主要污染物，实现评价因子降维的目的。然后结合BP神经网络，构建PCA-BP神经网络评价模型，同时利用主成分分析法的评价结果对PCA-BP神经网络评价模型的评价结果从侧面进行验证，就评价效果而言，PCA-BP神经网络评价模型既避免了单因子评价法中某一评价因子将其他因子的信息完全覆盖的弊端，同时也避免了主成分分析法评价结果的过分乐观，因此PCA-BP神经网络评价模型评价结果更为客观真实。总体来说，PCA-BP神经网络评价模型在解决了水质评价中评价指标权重难以合理确定，评价模型过于复杂、评价结果不合理等问题的基础上，为六合区的水资源保护与治理工作提供了参考。