重费米子化合物CemMnIn3m+2n(m=1,2,3;n=0,1,2;M=Co,Rh,Ir,Pt及Pd)的角分辨光电子能谱研究
2021-08-30罗洋宋姣姣赵尹陬孟建桥
罗洋,宋姣姣,赵尹陬,孟建桥
中南大学物理与电子学院,湖南省长沙市岳麓区麓山南路932号,410083
目录
I.引言 94
II.实验方法与理论模型 96
A.安德森模型 96
B.费米面 97
C.共振光电子能谱 98
III.结果与讨论 98
A.电子结构的维度 99
1.CeIn399
2.Ce2MIn899
3.CeMIn599
4.CePt2In7100
5.讨论 100
B.近藤共振 101
1.CeIn3101
2.Ce2MIn8101
3.CeMIn5102
4.CePt2In7103
5.讨论 103
C.电子结构随温度的变化 104
1.Ce2MIn8104
2.CeMIn5105
3.CePt2In7106
4.讨论 107
D.f电子与导带电子杂化 107
IV.总结与展望 108
致谢 109
参考文献 109
I.引言
重费米子材料以其丰富的物理图像,长期以来持续成为强关联电子体系,尤其是非常规超导领域的研究重点。该类材料所表现出的丰富物理性质如顺磁性、铁磁性、反铁磁性、超导电性、铁磁性/反铁磁性与超导电性共存、近藤绝缘体及拓扑近藤绝缘体等,以及其在外在调控下(如压强、磁场和化学掺杂等),低温时所表现出的各种奇异行为如量子临界、非费米液体等引起了凝聚态实验和理论物理学家的极大兴趣。这类材料一般包含镧系(如Ce、Pr、Sm、Yb等)或锕系元素(如U、Np、Pu等)以及少数部分的d电子元素(如LiV2O4和CaCu3Ir4O12)。这些元素原子往往含有未填满的f壳层(4f或5f),所以单个离子一般带有固有磁矩。在较高温度下,随着温度的降低,导带电子与局域f电子的磁矩发生自旋翻转散射,也就是所谓的非相干近藤散射,使得材料的电阻率在经历一个极小值之后表现出对数函数的温度依赖特征[1]。当温度继续降低,近藤耦合相互作用强度变大,导带电子会对局域磁矩逐渐产生屏蔽作用,最后局域磁矩被完全屏蔽而形成一个无磁性的自旋单态,并在费米能级附近出现共振态即近藤共振态[1]。在实际的重费米子材料中,局域磁矩通常是按晶格周期性排列的,相邻局域磁矩之间的间距往往超过了所谓的Hill极限[2],也就是说相邻离子上f电子的波函数几乎没有重叠(这导致f电子相对局域,并且具有较强的局域库仑相互作用),因而几乎没有直接相互作用。但是相邻局域磁矩能够通过与导带电子的作用产生间接的磁相互作用(即所谓的RKKY相互作用)[3-5],因此,晶格上的一个个磁矩不再是分离的近藤散射中心,而是共同构成一个相干的整体,此时会存在所谓的晶格相干杂化效应。导带电子与f电子发生的杂化会在费米能级附近产生具有一定色散的准粒子能带,准粒子的有效质量最高可到达自由电子质量的1000倍以上,因而这类材料被称为重费米子材料[6-11]。在重费米子材料中,其低能电子结构往往是由电荷、轨道、晶格及自旋自由度共同决定的,杂化后的f电子一般认为具有局域与巡游的二重特性,使得该体系变得复杂而难以理解。但因为容易通过改变温度、压力、磁场等多种方式对其电子组态进行微观调控,使得重费米子材料成为研究磁性与非常规超导电性关系以及量子临界点附近各种奇异物理特性的优良平台。
目前,在众多重费米子材料中,研究最为广泛的是U-基和Ce-基化合物。本文主要针对Ce-基重费米子化合物中得到极大关注的CemMnIn3m+2n(m=1,2,3;n=0,1,2;M=Co,Rh,Ir,Pt及Pd)系列化合物。此类化合物中,M一般代表d电子元素(如Co、Rh、Ir分别具有3d、4d、5d电子),晶体结构可视为由m层的CeIn3和n层的MIn2沿c轴交替堆垛而成。目前,该系列化合物可细分为五个子系列,分别是晶体为立方结构的CeIn3(m=1,n=0)、四方结构的CeMIn5(m=1,n=1)、四方结构的Ce2MIn8(m=2,n=1)、体心四方结构的CeM2In7(m=1,n=2)以及四方结构的Ce3MIn11(m=3,n=1)。在以上五个系列化合物中,CeIn3层间距离按照CeIn3≤Ce3MIn11≤Ce2MIn8≤CeMIn5≤CeM2In7的顺序依次增大,层间耦合相互作用逐渐减小,是研究晶体结构各向异性对材料物理性质影响的良好平台。在这些材料中,Ce3PtIn11(Tc=0.32 K)[12-14],Ce3PdIn11(Tc=0.42 K)[15,16],Ce2CoIn8(Tc=0.4 K)[17],Ce2PdIn8(Tc=0.7 K)[18,19],CeCoIn5(Tc=2.3 K)[20]和CeIrIn5(Tc=0.4 K)[21]均在常压下超导;CeIn3(TN=10 K)[22],Ce2RhIn8(TN=2.8 K)[23],CeRhIn5(TN=3.8 K)[24]和CePt2In7(TN=5.2 K)[25]在常压下均为反铁磁体,且都可以通过外加压力调控出超导相,最大超导转变温度依次为0.2 K[22],2 K[22],2.1 K[24]和2.1 K[25]。在Ce2IrIn8中,目前的实验还没有测量到磁有序态[26-29]。在CemMnIn3m+2n系列化合物中,实验发现了重费米子超导体中较高的超导转变温度(2.3 K,CeCoIn5),反铁磁有序与超导电性的共存,磁/压力诱导的量子临界等特性,使得这类化合物变得尤为特殊[20]。
在镧系元素中,Ce原子f壳层只含有1个f电子,原子基态为4f15d16s2,因而正常情况下的Ce离子是具有磁矩的(2.45μB),由此引起Ce-基重费米子化合物中丰富的物理性质。通常,局域的f电子能级在费米能级以下2~3 eV,经过近藤散射之后出现的近藤共振态是被重整化的f电子态,一般出现在能量略高于费米能级的位置。因为能量略高于费米能级,近藤共振态不容易被光电子能谱实验探测到,普通光电子能谱实验在费米能级附近探测到的4f强度一般为近藤共振态的尾部[11]。近年来角分辨光电子能谱(angleresolved photoemission spectroscopy,ARPES)的能量和动量分辨率显著提高[11,30-32],能更好地探测近藤效应所产生的共振态[33-47]、f电子与导带电子杂化产生的重准粒子能带[37-59]、自旋轨道耦合效应引起的与态[34-47]及其进一步由晶体电场引起的晶体场劈裂态[40-42,44,45],甚至由电子与其他多体相互作用(如电—声子耦合)引起的扭折等结构。由于ARPES实验本身对样品表面非常敏感,所以Ce-基重费米子化合物晶体结构的特殊性、电子结构的各向异性和表面效应等都对实验的开展和数据分析提出了挑战。
本文回顾了CemMnIn3m+2n系列化合物的光电子能谱研究,整理这一系列化合物的重要的实验结果,并归纳总结,最后在文末做出适当的展望,为重费米子材料理论模型的完善提供信息。本文主要结构如下:第一部分为本节,主要为背景介绍;第二部分主要为实验设计和理论基础;第三部分主要介绍CemMnIn3m+2n系列化合物的光电子能谱结果,并做适当的讨论;第四部分则是总结和展望。
II.实验方法与理论模型
在本节中,我们将讨论Ce-基重费米子材料ARPES实验中的光子能量选择问题,以及不同理论模型中的能带结构,主要包括f电子谱的共振增强、重准粒子产生过程、f能带的自旋轨道耦合、晶体场劈裂效应以及费米面的拓扑结构等。由于本文主要是对实验结果的总结,所以在本节中不对具体的物理过程做深入的理论分析。
A.安德森模型
在重费米子材料中,描述重准粒子形成过程的理论模型主要是单杂质安德森模型(Single Impurity Anderson Model,SIAM)和周期性安德森模型(Periodic Anderson Model,PAM),两者在理论框架和光电子能谱上存在明显的差异。
在单杂质安德森模型中,f电子是局域的,并且镶嵌在导带电子海中的孤立杂质磁矩也源于f电子,两个相邻稀土离子之间的磁矩是分离的,不相干的,各自为近藤散射中心。因此在单杂质安德森模型理论框架中,随着温度的降低,材料中导带电子与局域磁矩先经历反铁磁自旋翻转散射使得材料的电阻率曲线表现为对温度呈对数依赖关系(ρ~lnT);当温度降低临近近藤温度(TK),导带电子开始屏蔽局域磁矩并伴随着近藤共振态的产生,材料的电阻率曲线开始偏离对数函数依赖关系;最后,当温度远小于TK时,局域磁矩完全被屏蔽而形成一个无磁矩的自旋单态,此时无色散的近藤峰也达到最强。整个温度变化过程中只存在一个特征能量尺度—TK,它表征了费米能级附近共振态的能量位置(~TK)及能隙宽度(Δ~TK),同时将其能带结构的温度变化分为两部分,即TK之上的反铁磁自旋翻转散射和TK之下的屏蔽散射过程[60]。
作为单杂质安德森模型在周期性晶格上的拓展,周期性安德森模型中不仅考虑了高温下局域磁矩的近藤散射过程和低温下磁矩屏蔽过程,还引入了局域磁矩间的相干过程即所谓的晶格相干杂化效应。当温度低于特征温度――晶格相干温度T*(Tcoh)时,各晶格上的局域磁矩不再是单个孤立的散射中心而是相干的集体的量子整体,期间f电子会与导带电子发生杂化而形成准粒子,使得电阻率曲线在T*呈极大值并在更低温度与温度成二次方关系。所以在PAM的理论框架下,材料存在两个特征能量尺度:近藤温度TK和晶格相干温度T*。此时,f电子是具有局域巡游二重性的,而费米能级附近的共振态也因为f/d杂化而存在一定程度的色散(杂化强度越强往往色散越大)。目前,对重费米子材料广泛的光电子能谱研究表明单杂质安德森模型仅适用于弱杂化的强局域f电子材料,而周期性安德森模型能够更好的描述强杂化的弱局域f电子材料中费米能级附近准粒子的产生过程[11,61]。
图1为周期性安德森模型中费米能级附近准粒子产生的简单示意图。[61]在周期性安德森模型框架中,费米能级之下的f能级(εf,能谱中常称为f0终态峰)被重整化到费米能级附近(Ce/Yb基重费米子材料中略高/低于费米能级)形成一个新的f平带(ε′f,即所谓的近藤共振态),之后f电子平带与强色散导带(εd(k))发生杂化产生如图1(a)所示的新的上下两支准粒子能带E+和E-,这两个能带的色散关系可以用如下方程表示:
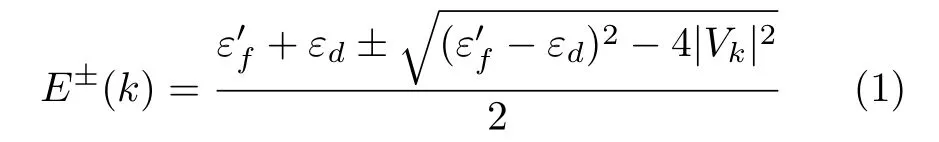
Vk代表f/d电子之间的杂化强度。在Ce-基重费米子材料中,E+往往是在费米能级之上,为非占据态,而E-才能被一般的ARPES探测到(如图1(b))。一般而言,上下两支杂化能带之间会有一个小的直接能隙(杂化能隙,Δ~10 meV),而新的准粒子能带的费米动量会发生变化(f电子参与构成费米面),并伴随着准粒子有效质量的增大(自由电子质量的10~1000倍)[61]。此外,f/d杂化还涉及到轨道的对称性,所以杂化过程是具有能带依赖性的。
上文中讨论的是最简单的杂化过程,如果我们进一步考虑f态的自旋轨道耦合及晶体场劈裂效应,重费米子材料的低能激发态将会变得更加复杂。如上文所提到的,Ce原子基态为4f15d16s2,f壳层只含有1个f电子。考虑自旋轨道耦合之后f电子会具有一个六重简并的基态(总角动量为5/2,也即态或近藤共振态)和八重简并的激发态(总角动量为7/2,即所谓的自旋轨道耦合边带态),两个态之间的能量间距一般为几百个meV。在实际的晶体材料中,Ce离子是处于其周围晶格环境所构成的晶体电场中的,所以这两个态会进一步发生劈裂。比如,在一个简单的四方晶体结构中,和态会分别劈裂为3和4个克莱默双态(Kramer doublet),而相邻双态之间的能量间隔一般为几个或几十meV。这些更低简并度态与导带电子的杂化将会使f电子与导带电子的杂化过程变得相当复杂,影响费米能级附近的低能激发过程,进一步的改变材料的宏观热力学、磁学等性质,同时也会对材料的特征温度产生影响[62,63]。在这些复杂的相互作用下,理论上的准确描述变得非常困难,因此使用光电子能谱直接观察材料中的自旋轨道耦合边带和晶体场劈裂态,对理解材料的基本物理性质是极为重要的。
综上所述,理论预期在Ce基重费米子材料中:随着温度的降低,首先可以探测到逐渐增强的4f1平带和态)以及位于费米能级之下2~3 eV处的(f1→f0)电离峰;当温度低于相干温度,f电子与导带电子杂化开始出现并愈来愈强,费米动量发生变化。如果能量和动量分辨率足够高,自旋轨道耦合和晶体场效应都可以被探测到。如图2所示为Yb-基重费米子材料YbRh2Si2中的晶体场劈裂态与导带杂化的ARPES谱[64]。图2(a)-(c)中费米能级附近均出现了明显的4f平带,分别对应Yb原子在四方晶体电场劈裂出的四个克莱默双态。四个平带中,具有与更高束缚能处导带相同波函数对称性的平带才会与之发生杂化。
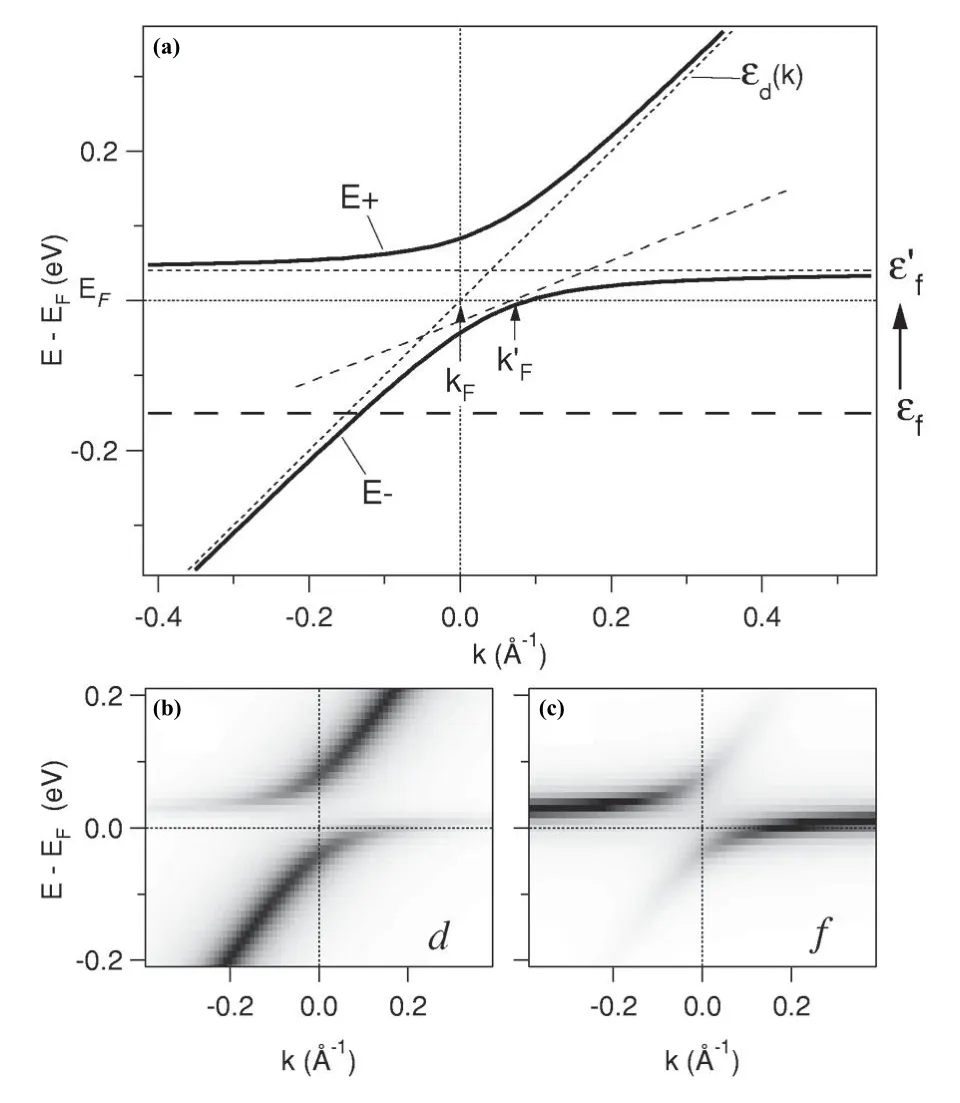
图1.(a)周期性安德森模型框架下费米能级附近准粒子产生示意图。(b)、(c)分别为费米能级附近导带电子与f电子谱强度[61]。
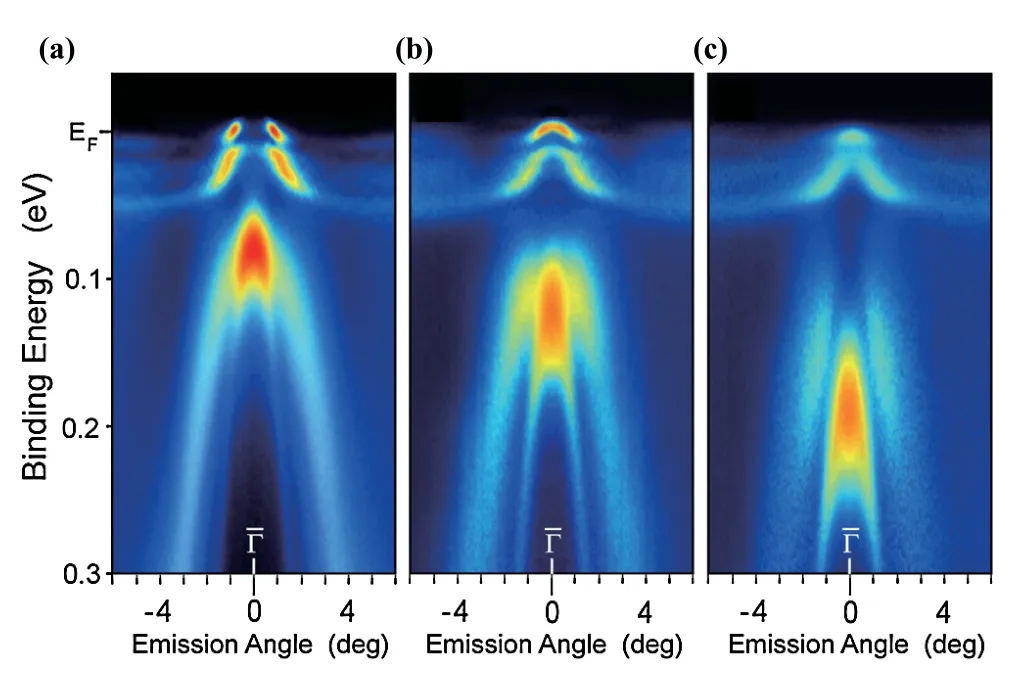
图2.YbRh2Si2的Si终止面的ARPES谱。[64](a)沿-方向;(b)、(c)平行-方向,距离¯Γ点分别为0.03和0.06倍[¯Γ,¯X]长度。
B.费米面
一般情况下,当材料的晶体结构具有更强的二维性,其电子结构往往也会表现出较强的二维特征,即具有类似柱状结构的费米面。然而,强关联电子材料中的电子关联作用及动量相关的杂化效应等会在一定程度上改变材料的费米面结构,使得费米面与晶体结构的维度不能再简单对应。
在重费米子超导中,大量的研究表明费米能级附近的重准粒子是参与超导电子配对的,尽管关于其配对机制一直存在争议[10]。基于重费米子超导中奇异的超导与磁有序共存现象和量子临界行为,众多理论和实验科学家认为超导与自旋涨落相关[8,65]。基于磁涨落调制超导的理论工作表明,具有更强二维晶体结构和电子结构的材料可以实现更高的超导转变温度[66,67]。实验也证实,在CemMnIn3m+2n系列化合物中,超导转变温度从CeIn3中的0.2 K到CeCoIn5中2.3 K,简单立方晶格到准二维的简单正方晶格的改变使超导转变温度提高了一个数量级,意味着二维晶体结构的确有利于提高超导转变温度[21,68]。如上文所述,CemMnIn3m+2n系列化合物具有从三维到准二维变化的晶格结构,所以进一步研究这些化合物的电子结构,将会有益于了解材料晶体结构和电子结构维度与超导转变温度的关系,其直接与f电子对费米能级的贡献大小有关。随着温度的降低,局域的f电子与巡游导带电子间的Kondo效应增强产生杂化,f电子参与构成费米面。这一过程中费米动量会发生明显的变化,理论预言能够观察到费米面体积在温度跨过T*的过程中发生大的改变[69-74]。图3为密度泛函(DFT)和密度泛函理论加动力学平均场理论(DFT+DMFT)计算得到的不同温度下的CeIrIn5的费米面[74]。高低温时的费米面变化是非常明显的,且具有清晰的能带依赖性。
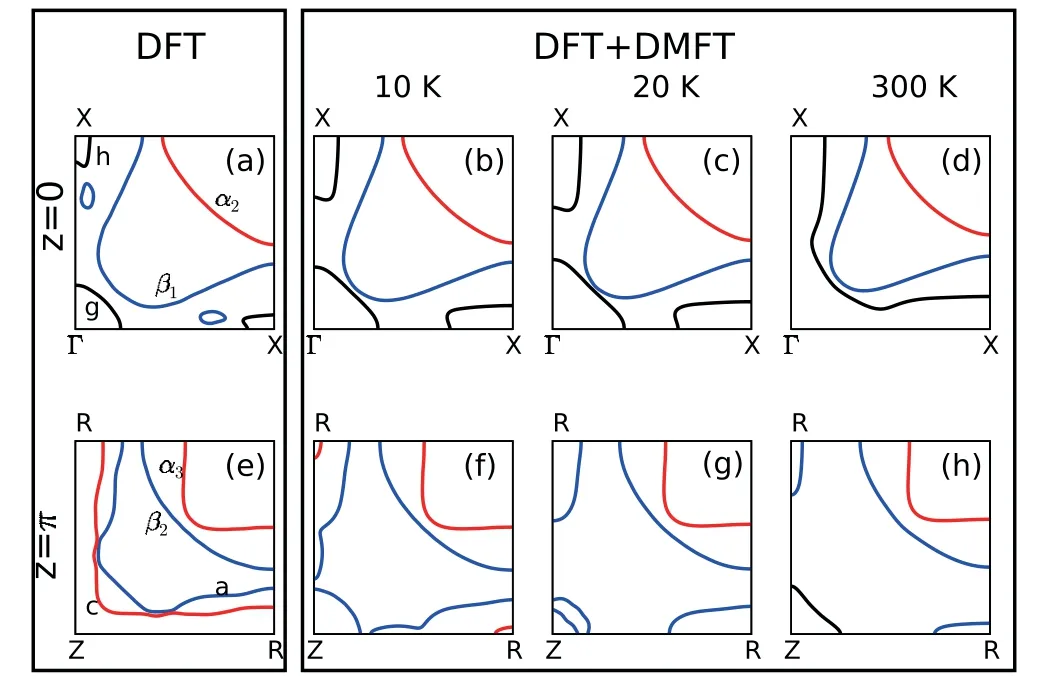
图3.理论计算的CeIrIn5费米面。[74](a)、(e)分别为基于DFT理论计算的Z=0、Z=π平面内的费米面。(b)-(d)和(f)-(h)分别为基于DFT+DMFT理论计算的T=10 K、20 K、300 K时Z=0、Z=π平面内的费米面[74]。
C.共振光电子能谱
在光电子发射过程中,不同元素的不同轨道电子的光电离截面与光子能量密切相关[75]。因此,ARPES实验往往会选择合适的光子能量来获得特定轨道的电子信号。早先对Ce-基重费米子材料的研究,经常通过不同能量光子的能谱差值来提取4f电子的信号[76],但这样会存在测量动量位置(垂直样品表面,kz)、范围不一致,能量分辨率不同等问题。目前普遍利用共振角分辨光电子能谱(Resonant-ARPES)来有效提取f电子信息,该方法已经广泛应用于一些金属和d电子、f电子的强关联材料[77-80]。
Resonant-ARPES是通过共振吸收增强来提高光电发射谱中f电子的信号强度。Ce-基材料常用的共振光子能量为882.5 eV和121 eV,分别对应3d→4f和4d→4f共振吸收[77,79,80]。两种光子能量都能够极大的增强f电子的信号,同时还能保证较好的体分辨能力。以Ce基材料的4d→4f共振吸收为例,当入射光子能量hv~121 eV时,部分光子作用在Ce的4d电子,发生4d→4f跃迁,使得Ce的4f态上短暂地存在两个电子,之后经历俄歇过程:其中一个电子退激发回4d态并将能量传递给另一个电子使其成为光电子。与此同时,入射光子直接作用在4f电子,激发其成为光电子。最终的4f电子的光电发生过程应该是这两个过程的相长干涉叠加,使得4f电子的光电离界面在121 eV附近出现法诺共振(Fano resonance)增强现象,4f电子的光电发射信号明显增强[77,81]。如图4所示为Resonant-ARPES探测的CeCoGe1.2Si0.8费米能级附近的能带结构,可以看到共振谱中4f信号明显增强[82]。
III.结果与讨论
在CemMnIn3m+2n系列化合物中,CeIn3层间距离按照CeIn3<Ce3MIn11<Ce2MIn8<CeMIn5<CeM2In7的顺序依次增大,晶体结构的二维性增强。其中,ARPES研究主要集中在CeIn3和CeMIn5,而Ce3MIn11系列化合物合成的较晚,因此研究的较少。本文回顾了CeIn3,Ce2MIn8,CeMIn5和CeM2In7的光电子能谱研究,重点关注材料的晶体结构和费米面的拓扑结构与重费米子材料超导转变温度的关系;归纳了近藤共振峰的强度和f电子自旋轨道耦合强度及可能的晶格电场效应劈裂,讨论4f电子的局域/巡游特征;比较不同温度下的费米面体积,观察f/d杂化随温度的变化,总结重准粒子的产生过程。
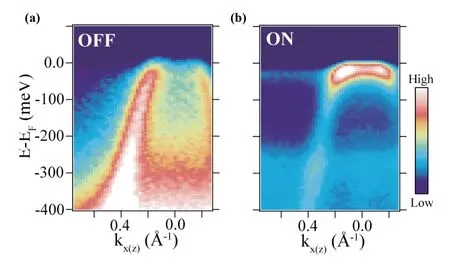
图4.(a)、(b)分别为CeCoGe1.2Si0.8的非共振和共振(4d→4f)ARPES谱[82]。
A.电子结构的维度
近十年来,多个课题组使用ARPES对CemMnIn3m+2n系列化合物的电子结构进行了研究,发现在所有已被测量的化合物中,费米面总体上具有很大的相似度。布里渊区角落处往往具有比较大的以角落为中心的费米面,且通常具有更好的二维性,而以布里渊区中心和边界中点为中心的费米面通常是比较三维的。总体上,材料费米面的各向异性强度并不与材料晶体结构的二维性一致。
1.CeIn3
图5展示了CeIn3的顺磁态费米面[49]。图5(a)表现出复杂的费米面结构,包括一个以Γ−Z为中心的费米面d和一个以R点为中心的椭圆形口袋结构a。图5(b)中,在ΓXM面上观察到一个以M点为中心的四方形口袋d3和以Γ点为中心的双环结构d2。同样在ZAR平面上(图5(c)),也观察到了一个以Z点为中心的四方结构d1和一个以R点为中心的椭圆形结构a。结果表明CeIn3的费米面存在明显的三维特性,体现的是其电子结构的三维性,与其简单立方结构一致。
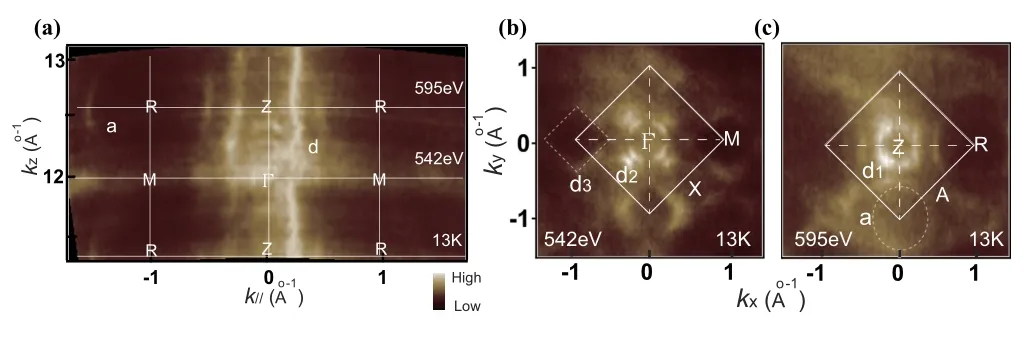
图5.CeIn3的顺磁态(13 K)费米面[49]。(a)、(b)、(c)分别为ΓZRM、ΓXM、ZAR平面的费米面。
2.Ce2MIn8
如图6所示,(a)和(b)为变光子能量测得的低温下Ce2RhIn8的三维费米面及不同光子能量测得的kx−ky平面内费米面[48],(c)为Ce2PdIn8在Γ和Z平面内费米面[48,58]。可以发现Ce2RhIn8的费米面都没有明显的kz色散,表明这个材料的电子结构有很好的二维性。低温下不同光子能量测的Ce2RhIn8的费米面具有相似的电子结构,如以M点为中心的四个大的电子型费米口袋和Γ附近的一个空穴型口袋,表明其电子结构kz色散非常弱,与图6(a)中的结论一致。从图6(c)可以看出,X点的跑道型费米口袋以及以M点为中心的几个大的费米面在不同kz平面之间只有非常小的改变,而Γ点费米口袋与Z点费米口袋在形状和大小上差异较大,表明Ce2PdIn8的电子结构大部分是准二维的。
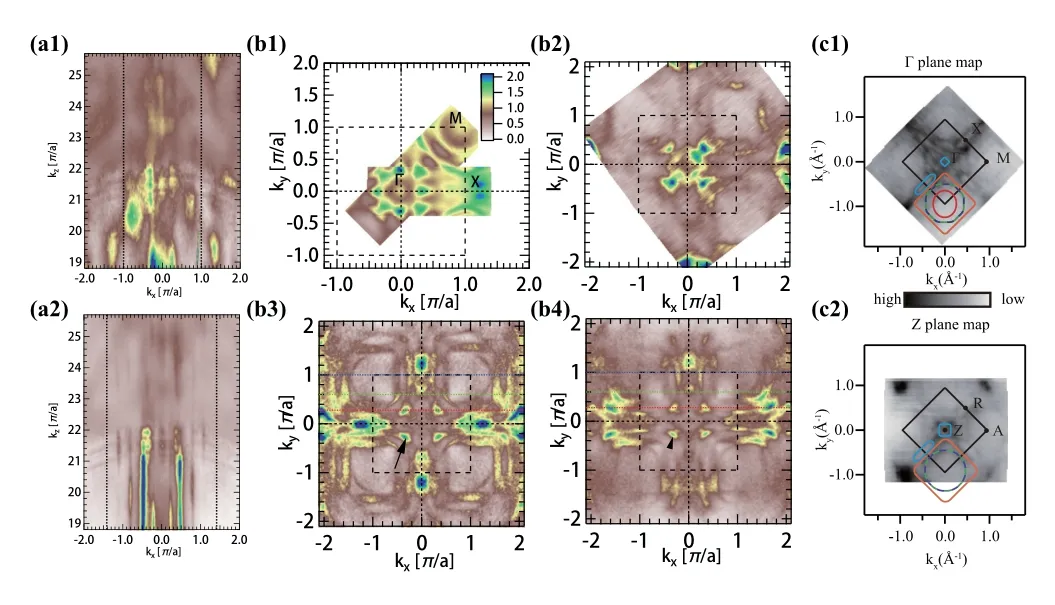
图6.Ce2MIn8费米面。(a1)、(a2)分别为Ce2RhIn8沿Γ-X和Γ-M方向的kz色散[48];(b1)-(b4)Ce2RhIn8的kx-ky平面内费米面,光子能量分别21.2 eV、80 eV、94 eV和105 eV[48];(c1)、(c2)分别为Ce2PdIn8在Γ、Z平面内费米面[58]。
3.CeMIn5
图7(a)-(c)分别为低温下CeCoIn5[50]、CeRhIn5[53]和CeIrIn5[44,52]的 费 米 面。由图7(a1)、(a2)、(b1)、(b2)和(c1)可知,三个化合物中布里渊区角落M点附近能带沿kz方向的色散较弱,与三者的准二维的晶体结构一致。从图中也看出部分费米面存在显著三维特性,如CeRhIn5的γ费米面。比较三种化合物ΓXM和ZAR平面的费米面(图7(a3)、(a4)、(b3)、(b4)和(c2)),可以发现以M点为中心的花瓣形和方形型费米面、Γ点附近小的费米口袋在三种材料中都观察到了,而Z点附近的小口袋和A点附近的圆形和方形费米面同样都在CeCoIn5和CeRhIn5的ZRA面观察到了,表明三者的电子结构非常相似。CeMIn5系列化合物的电子结构是三维性与二维性共存的。
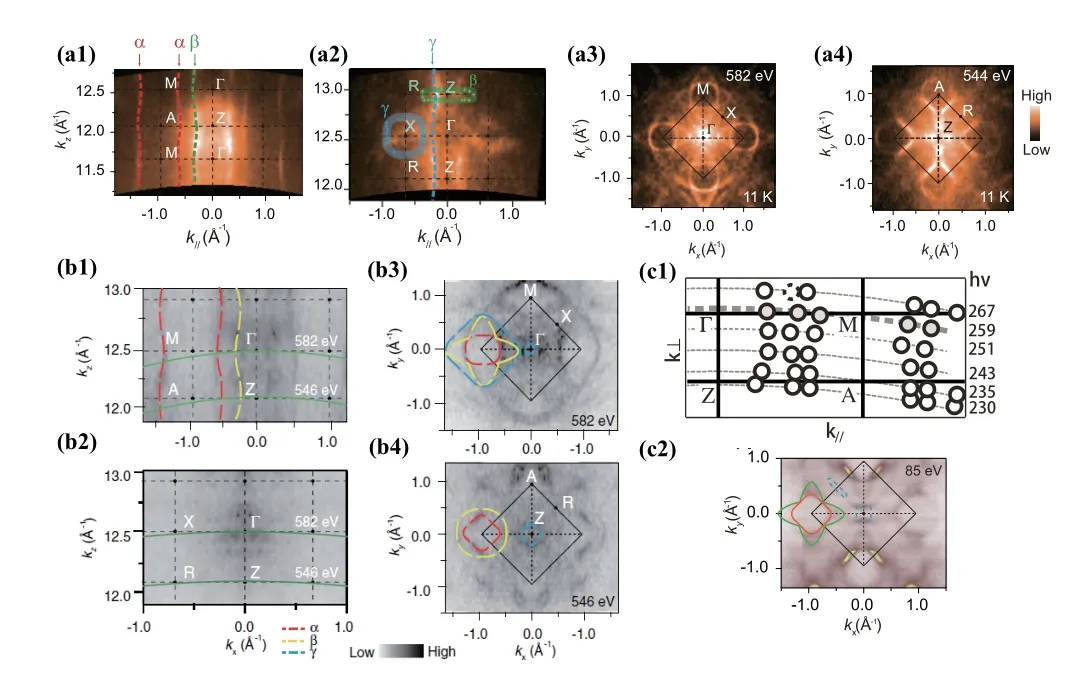
图7.CeMIn5费米面。(a)CeCoIn5费米面[50];(b)CeRhIn5费 米 面[53];(c1)、(c2)分 别 为CeIrIn5在ΓZMA[44]、ΓXM[52]平面内费米面。
4.CePt2In7
图8为低温下CePt2In7的费米面拓扑结构[51,56,59]。变光子能量测量的ΓXRZ平面的kz色散(图8(b)和(c))随光子能量变化巨大,布里渊区中心(Γ/Γ′)和边界中点(X/X′)附近的费米面(图8(d))的形状也随光子能量变化,这表明费米面具有显著的三维特性。另外从 图8(d)可以发现在布里渊区角落(M/M′)处,两相似的费米口袋在不同光子能量下测得的费米面都观察到了,表明此处费米面具有很好的准二维性。这些都与理论计算符合的较好。CePt2In7的电子结构是三维与二维共存的,与CeMIn5系列化合物类似。
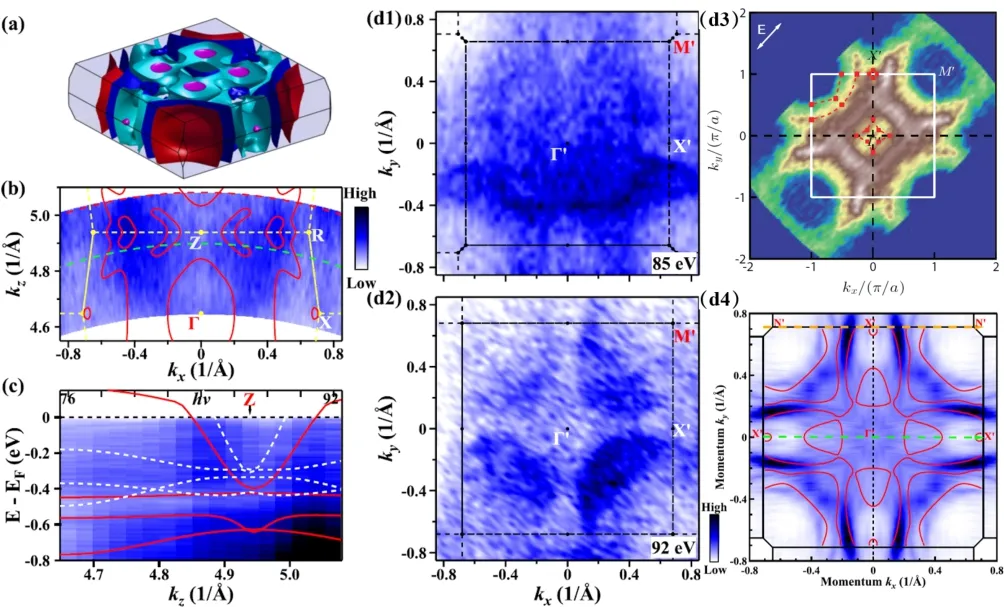
图8.(a)理论计算的CePt2In7费米面[56,59];(b)20 K时CePt2In7在ΓXRZ面内费米面[56,59];(c)从(b)中提取的沿Γ-Z-Γ方向的色散[56,59];(d1)-(d4)不同kz时,kx-ky平面内费米面,光子能量分别85 eV(20 K)[56,59]、92 eV(20 K)[56,59]、21.2 eV(20 K)[51]和100 eV(10 K)[59]。
5.讨论
综上所述,在CemMnIn3m+2n系列化合物中,具有三维晶体结构的CeIn3拥有最强三维性的电子结构,最强二维晶体结构的CePt2In7具有与CeMIn5系列化合物类似的三维与二维共存的费米面,而Ce2MIn8系列化合物电子结构的二维性最强。由此可见,这一系列材料的电子结构维度与它们的晶体结构各向异性强度并不一致。在这一系列材料中,CeCoIn5、Ce2PdIn8及CeIrIn5在常压下超导,而CeIn3、Ce2RhIn8、CeRhIn5及CePt2In7常压下为反铁磁体,且均可通过加压调控处超导相。结合以上费米面数据可以发现,尽管超导转变温度自CeIn3(加压)到CeCoIn 5(2.3 K)增加了一个数量级,但是具有越二维电子结构的材料并不总是具有更高的超导转变温度。同时,我们也可以注意到结构更加二维的材料可能也未必表现出更强超导电性。
目前,对这系列材料的费米面数据已经反映了许多重要的特征,但是很多费米面的细节依然是不够清晰的,不论是沿kz方向还是垂直kz动量平面内的费米面数据。清晰地测量各材料的各个费米面,尤其是一些小的费米口袋,将有助于对材料的电子结构及电子结构的改变做更多定量的分析(如费米口袋面积大小等)。此外,这类材料超导转变温度以下的电子结构数据目前是缺失的,尽管重费米子超导体的超导转变温度普遍很低,但是能够获得这一系列重费米子超导体(如CeCoIn5)在Tc以下的费米面数据对理解重费米子超导的机制是极为重要,这也是从事重费米子材料研究的实验物理学家们需要继续努力的方向。
B.近藤共振
随着光电子能谱技术的发展,越来越多研究组利用共振光电子能谱研究重费米子材中的近藤物理。本小节回顾了CemMnIn3m+2n系列材料中近藤共振态、共振态的自旋轨道耦合态及晶体场劈裂态相关的能谱数据,总结了各材料中的共振态强度、自旋轨道耦合强度、晶体场劈裂能量尺度对材料的依赖性。
总体上,各材料中费米能级附近被探测到的近藤共振峰的尾部都不是特别的强,但是依然随材料不同表现出差异。所有化合物中f电子的自旋轨道耦合强度都位于250 meV~300 meV之间,部分材料中还观察到了4f态由晶体电场效应引起的劈裂态。
1.CeIn3
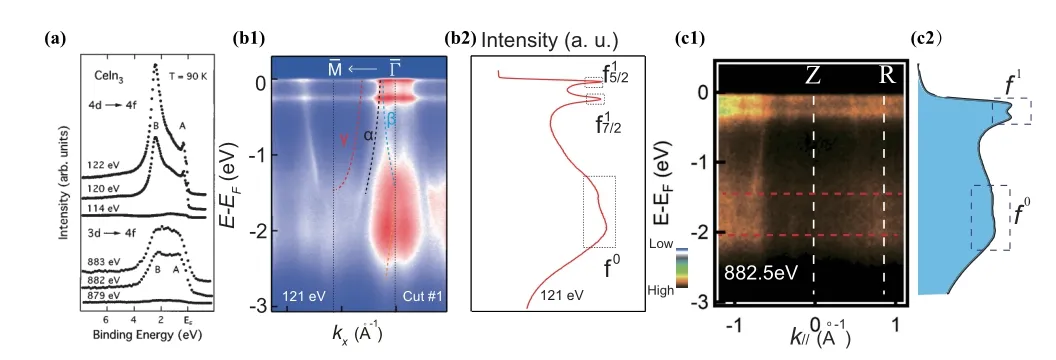
图9.CeIn3光电子能谱。(a)4d→4f和3d→4f的共振与非共振光电子能谱[41];(b1)、(b2)(001)方向的In终止面沿Γ′-M′方向的4d→4f共振能带结构和对应的能量分布曲线[55];(c1)、(c2)沿Z-R方向的3d→4f共振能带结构和对应的能量分布曲线[49]。
CeIn3的近藤共振态的测量最早是在1997年报道的,如图9(a)所示[41]。在这篇文章中,通过使用安德森杂质模型拟合了3d→4f和4d→4f共振光电子能谱数据(角积分谱),得到了CeIn3体态中的4f电子的εf~1.5 eV,自旋轨道耦合能量Δso~280 meV,f/d杂化强度为Δ~69 meV等参数。近几年,张云等人对CeIn3进行了3d→4f(882.5 eV)[49]和4d→4f(121 eV)[49]的共振角分辨光电子能谱研究(图9(b)和(c)),观察到的f电子自旋轨道耦合劈裂态的位置分别为费米能级以下300 meV和260 meV,4f0终态峰均位于费米能级以下2 eV左右,并在1.5 eV处还发现了一个源于杂化扩散的平带。此外,在两种共振光电子能谱图中,与峰强度之比、4f1与f0峰强度之比均具有较大值,明显不同于其它化合物(见下文)。
2.Ce2MIn8
图10为Ce2MIn8系列化合物的共振光电子能谱数据[45,57,58]。图10(a1)、(a2)分别为Ce2CoIn8和Ce2RhIn8的4d→4f共振(122 eV)与非共振(114 eV)光电子能谱,图10(a3)为(a1)和(a2)对入射光通量归一化之后的共振谱减去非共振谱后得到的谱[45]。图10(b)为Ce2IrIn8在15 K的4d→4f共振(b2)与非共振(b1)角分辨光电子能谱及相应的角积分谱(b3)[57]。图10(c)为Ce2PdIn8在11 K的4d→4f共振(c2)与非共振(c1)角分辨光电子能谱及相应的角积分谱(c3)[58]。从Ce2MIn8的共振光电子能谱图可以看到,以上四个化合物都存在明显的f0、态和终态峰,分别位于在−2.5 eV、−250 meV及费米能级附近。可以发现,Ce2MIn8的终态峰的强度均较弱,显著弱于终态峰,且4f1峰也是明显弱于4f0,这表明该材料内4f电子的巡游性较弱。
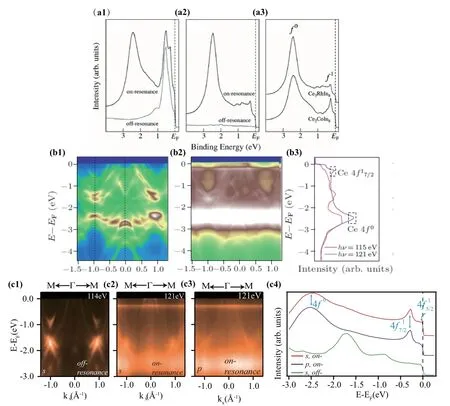
图10.(a)为Ce2CoIn8(a1)和Ce2RhIn8(a2)的4d→4f共振(122 eV)与非共振(114 eV)光电子能谱,(a3)为两者的能谱对光通量做归一化后的共振减非共振得到的谱。[45](b)为15 K时Ce2IrIn8的4d→4f共振(121 eV)(b2)与非共振(115 eV)(b1)ARPES。(b3)为(b1)和(b2)的角积分谱。[57](c)为11 K温度下s偏振入射光测得的Ce2PdIn8中沿Γ-M方向4d→4f非共振(114 eV)(c1)、s偏振(c2)及p偏振(c3)入射光共振(121 eV)光电发射强度分布图,(c4)为(c1)-(c3)的角积分谱[46,58,59]
3.CeMIn5
图11给出了CeCoIn5[47]、CeIrIn5[43,46]和CeRhIn5[43,46]的共振光电子能谱。如图11(a)所示,比较CeCoIn5共振谱(121 eV)与非共振谱(XPS,1486.6 eV),在−1.4 eV能量处出现了来源于体态的4f0终态峰;比较共振谱(121 eV)与非共振谱(117 eV),发现共振谱在−1.4 eV处谱重有显著增强,另外在费米能级附近预期的巡游4f态及其自旋轨道劈裂边带的位置(箭头所示)的谱重也有一定增强。在图11(b)中,可以发现CeIrIn5和CeRhIn5具有类似的谱型,一个强的位于−2.5 eV来源于4f0终态的峰,以及费米能级附近具有较低强度的态和其自旋轨道耦合边带态,分别位于费米能级和−280 meV附近。注意到CeIrIn5的峰与峰强度相当,而CeRhIn5的峰明显强于峰,作者认为CeIrIn5中4f电子与导带电子的杂化强度略高于CeRhIn5[43]。比较图11(b)和(c)可以发现,4d→4f和3d→4f共振谱都有f1和f0峰,但是相对强度不一样[43]。这可能是由于3d→4f共振谱具有更强的体态探测能力。CeMIn5中,局域的4f电子占据主导地位,只有很少的4f电子是巡游的,但是这部分巡游的4f电子决定了系统的低能物理特性,因此也决定了系统的低温特性。
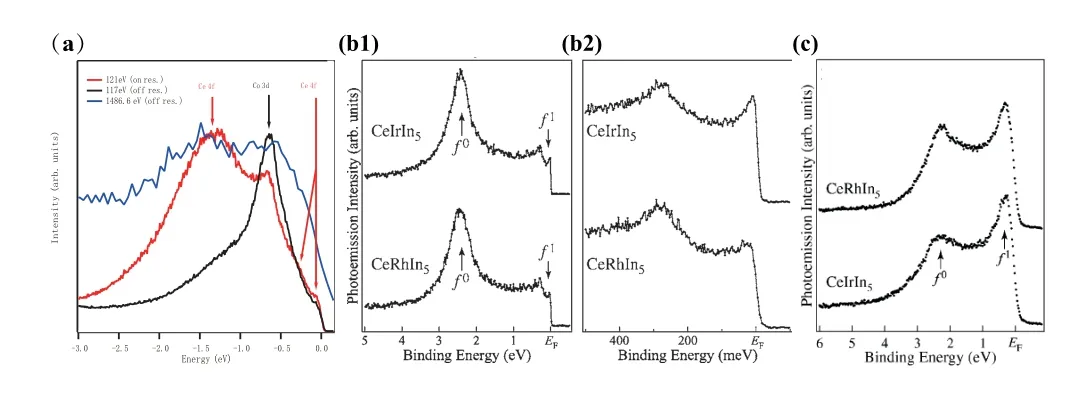
图11.CeMIn5的共振光电子能谱。(a)CeCoIn5的4d→4f共振光电子发射谱[47];(b)CeIrIn5和CeRhIn5的4d→4f共振光电子发射谱(122 eV)[46];(c)CeIrIn5和CeRhIn5中测量的3d→4f共振光电光电子谱(881 eV)[43]。
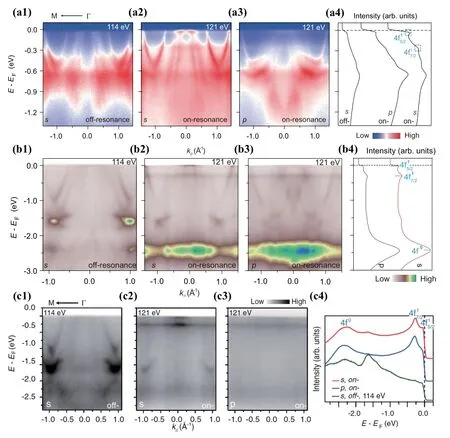
图12.CeMIn5沿Γ-M方向的4d→4f共振(on-)和非共振(off-)光电子能谱图。(a)CeCoIn5(11 K)[50]。(a4)为(a1)-(a3)的积分能量分布曲线。(b)CeIrIn5(12 K)[52]。(b4)为(b2)和(b3)的积分能量分布曲线。(c)CeRhIn5(8 K)[53]。(c4)为(c1)-(c3)的积分能量分布曲线。图的左下角给出了入射光子的偏振方向。
图12(a)-(c)分别为低温下CeCoIn5[50]、CeIrIn5[52]和CeRhIn5[53]的4d→4f共振ARPES数据。在三种材料的非共振谱(图12(a1)、(b1)、(c1))中,可以观察到明显的来源于Co、Rh、Ir的d电子和Ce的5d电子的导带。在共振谱中(图12(a2)和(a3)、(b2)和(b3)、(c2)和(c3)),4f电子态密度显著增强,可以清楚的观察到在费米能级(态)和−280 meV(态)附近的平带,其中s偏振时更为显著。在CeIrIn5和CeRhIn5中,还观察到了位于−2.3 eV附近的f0终态峰,与早先结果基本一致。
如图13(a)所示,30 K时,两种线偏振光源测得的CeRhIn5的4d→4f共振ARPES在移除费米狄拉克分布函数与能量分辨率的卷积函数后在Γ点附近的能量分布曲线显示出两个属于的晶体场劈裂态峰,分别位于1.5 meV(s偏振)和8 meV(p偏振)处[53]。从对CeRhIn5的非弹性中子散射数据可以知道,态经过四方晶格场作用产生的三个双重简并态的波函数为:Γ6=|±1/2〉,=0.78|±5/2〉−0.62|∓3/2〉,=0.62|±5/2〉+0.78|∓3/2〉,对称性如图13(c)所示。根据各劈裂态波函数的对称性和图12(a)中两个特征对光源偏振方向的依赖性,认为1.5 meV处的峰来源于Γ+7,8 meV处的来源于Γ-7,而Γ6态因为远在费米能级之上而没有被探测到。如图13(b)所示,通过高能量分辨率的测量,在CeIrIn5中也观察到了7个起源于和态的晶体电场劈裂态[52]。源于态的3个双重简并态分别位于−20 meV(Γ17)、−32 meV、−65 meV(Γ6)处,来自于态的4个双重简并态分别位于−272 meV、−294 meV、−318 meV、−341 meV处。但是,源于态的3个双重简并态之间的能量间隔不同于非弹性中子散射结果(基态与第一激发态之间能量间隔为4 meV,与第二激发态之间间隔为28 meV),可能是源自于多体效应的影响[83-85]。此外,对CeCoIn5的4d→4f共振ARPES温度依赖性的数据移除费米狄拉克分布函数与能量分辨率的卷积函数后(没有展示),同样发现了态的3个双重简并态,分别位于费米能级之上2 meV、9 meV和30 meV处[50],而这一结果与中子散射数据符合的很好。

图13.(a)CeRhIn5的在Γ点附近的4d→4f共振能量分布曲线[53]。曲线移除了费米狄拉克分布函数和能量分辨率的卷积函数。(b)s偏振和p偏振光测量CeIrIn5中费米能级附近的能量分布曲线[52,53]。橙色曲线代表p偏振光测量的能量分布曲线在移除费米狄拉克分布函数与能量分辨率卷积结果后的数据。(c)四方结构晶格中态的三个晶格电场劈裂双重态(、、Γ6)的波函数分布。[53](d)CeIrIn5中多重简并f态的晶体场劈裂示意图。[52]
4.CePt2In7
如图14,给出了低温下CePt2In7的4d→4f共振角分辨光电子能谱结果[56,59]。可以发现其4f0峰位于−2.5 eV处,自旋轨道耦合劈裂大概为300 meV。详细地分析图14(a3)、(b)可以发现,f0峰的强度远远大于f1;f1态的自旋轨道耦合劈裂带的4f15/2态强度非常弱,可能是因为该材料的4f电子具有强的局域性。通过对费米能级附近4d→4f共振(123 eV)谱(图14(c1))进行二次微分处理,发现f1态的自旋轨道耦合劈裂态的晶体场劈裂峰,终态的晶体场劈裂峰为位于−325 meV和−270 meV,终态的晶体场劈裂峰位于−75 meV和−15 meV。

图14.CePt2In7的4d→4f共振光电子能谱。(a1)和(a2)分别为20 K温度下沿Γ-X方向测量的4d→4f非共振(115 eV)与共振(121 eV)ARPES。(a3)为(a1)和(a2)的角积分谱。(b)为10 K温度下测量的Γ′M′方向宽能量范围的4d→4f共振(123 eV)光电发射强度分布图。(c)为10 K下沿Γ′M′方向费米能级附近4d→4f共振(123 eV)价带结构(c1)及其对应的二次微分结果(c2)[56,57,59,60]。
5.讨论
综上所述,在CemMnIn3m+2n系列化合物中,大部分材料的f0终态峰均位于−2.5 eV左右;而CeIn3在2 eV和1.5 eV处均存在强度峰,CeCoIn5则只在1.4 eV处出现峰。f0终态峰的能量位置差异可能是由探测的体态和表面态的比例差异造成的。不同材料的f1终态峰的强度随材料变化巨大,在三维晶体结构材料CeIn3中最强。同时,f1终态峰在各材料中均发生了自旋轨道耦合劈裂,其中CePt2In7的自旋轨道耦合劈裂最大,Ce2MIn8系列化合物中的自旋轨道耦合劈裂最小,CeIn3和CeMIn5系列化合物介于两者之间。此外,在CeIrIn5、CeRhIn5及CePt2In7中还发现了源自晶体场劈裂的峰,但是晶体场劈裂态在原始能带光电发射强度图中并不十分明显,需要对原始数据做费米狄拉克分布函数与能量分辨率卷积处理或者二次微分处理才能变得清晰,因此依然需要更高能量分辨率的数据。最后,比较各材料中与峰强度之比、4f1与f0峰强度之比可以发现,CeIn3具有最大的比值,CePt2In7和Ce2MIn8具有最小的比值,而CeMIn5的值居中。
C.电子结构随温度的变化
本节中,我们将会总结对CemMnIn3m+2n系列材料的温度变化光电子能谱数据。通过对高低温下测量的费米面和详细的温度变化能带色散数据的归纳,我们得到了两个重要的实验结论:(一)f/d电子的杂化过程并不总是在T*之下发生,而发生杂化之后的f电子的局域巡游性也没有普适的规律;(二)目前没有直接的光电子能谱数据在CemMnIn3m+2n系列材料中观察到非常剧烈的费米面变化(大量的f电子加入费米面),尽管在部分材料中探测到了一定程度的费米动量的改变。
1.Ce2MIn8
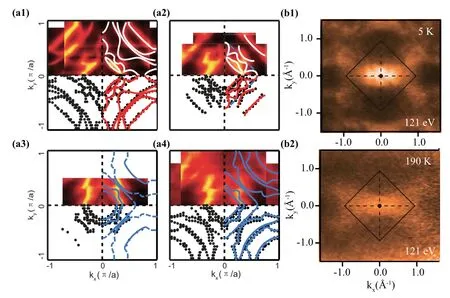
图15.不同温度下Ce2RhIn8的费米面。(a)入射光子能量为22 eV,测量温度分别为300 K,200 K,125 K,10 K[54,55]。带颜色的线代表推断的费米面。(b)温度为190 K、5 K时4d→4f共振条件下(121 eV)测得的Ce2PdIn8的费米面[58,59]。
图15(a)为F.Rodolakis等人测得的Ce2RhIn8费米面的变温结果[54]。比较测量温度为300 K(图15(a1))与10 K时的费米面(图15(a4)),可以发现三个最外层的费米面只发生了轻微的变化,而位于布里渊区中心附近的费米面随温度改变剧烈。这种改变主要体现为高温下的小口袋的消失以及星形空穴费米面劈裂成低温下的两个电子口袋,意味着在失去一个电子后费米面体积在高温下的塌缩。详细的温度测量数据,可以发现塌缩只在温度高于125 K时发生。F.Rodolakis等人认为这样一个塌缩行为开始在200 K左右(差不多是电阻率曲线极小值处,远高于晶格相干温度),并且认为这种行为是某种涨落引起的[54]。在Ce2MIn8系列化合物中,封东来研究组测量了Ce2PdIn8在高温和低温下的费米面(图15(b))。随着温度的降低,费米面的体积没有发生明显的改变,布里渊区中心区域的f电子谱权重明显增强[58]。这与他们在CeMIn5观察到的结果类似。
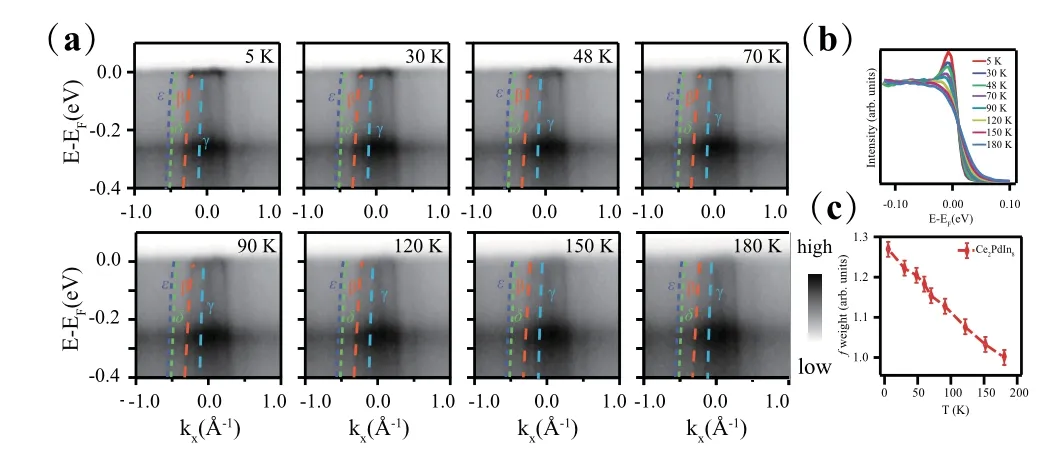
图16.Ce2PdIn8能带结构随温度的演化。[58](a)Γ-M方向共振谱随温度的演化情况;(b,c)f电子谱重随温度的演化。
图16(a)为封东来课题组在不同温度下测得的Ce2PdIn8沿Γ−M方向4d→4f共振(121 eV)ARPES数据[58]。低温下,费米能级附近存在明显的4f平带(图16(a1))。随着温度的升高,f态的谱权重逐渐减小并在150 K时变得不再清晰,这一点在提取的Γ点附近能量分布曲线的温度变化图中更加明显(图16(b))。此外,从费米能级附近Γ点左右的准粒子谱权重的温度变化曲线可以看到谱强度同样也是自最高测量温度开始随温度降低单调增加(T*~30K),这一结果与CeMIn5也很类似。但是,在相同结构的化合物Ce2IrIn8中,费米能级附近的f平带随温度升高变得模糊(如图17(a)、(b)所示),在温度高于T*~40 K之后就基本消失了,这一结果与CeMIn5和Ce2PdIn8都不一样[57]。但是,f电子谱权重却依然是自最高测量温度(80 K)开始随温度的降低逐渐增强的。此外,费米能级处的能量分布曲线温度变化图(图17(c))表明在温度跨过T*之后能带费米跨越的位置基本不变,说明Ce2IrIn8中可能也不存在较为明显的费米面改变。
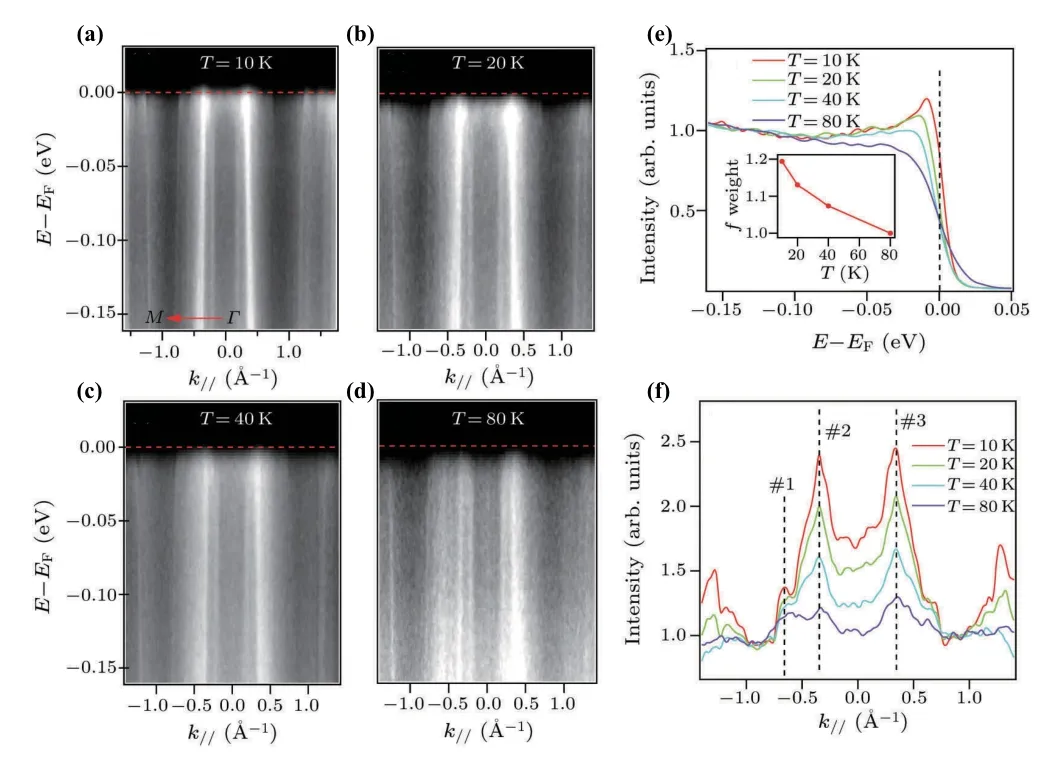
图17.(a1)-(a4)为Ce2IrIn8的沿Γ-M方向4d→4f共振(121 eV)ARPES从10 K到80 K的温度变化数据。(b)为对应温度下的角积分谱,插图为费米能级附近f电子谱权重的温度变化曲线。(c)为费米能级处能量分布曲线的温度变化图[57,58]。
2.CeMIn5
图18(a)-(c)分别为CeCoIn5[50]、CeRhIn5[53]、CeIrIn5[52]费米面随温度变化的数据。比较这三种化合物在高温和低温下的费米面,发现随着温度的降低,三个化合物的费米面并没有出现明显改变,只在Γ点附近出现了因为f/d杂化引起的谱强度增强。由于分辨率的关系,无法获得清晰的Γ点附近费米面的变化,但是总体上来说费米面改变是不大的。比较310 K,190 K,17 K温度下CeCoIn5的费米面与14 K时LaCoIn5的费米面(图18(a4)),可以看到两种化合物的费米面结构总体是非常相似的,表明即使在低温下CeCoIn5的4f电子对费米面的贡献也比较小。
图19(a)-(c)分别为CeCoIn5[50]、CeIrIn5[52]和CeRhIn5[53]沿Γ−M方向4d→4f共振(121 eV)ARPES的温度变化数据。随着温度的降低,三种材料的4f电子能带逐渐出现并变得越来越强,重准粒子能带与导带之间的杂化随着温度的降低愈加明显。值得注意的是在三种材料中都发现重准粒子能带出现的温度远高于从电阻率数据中得到的相干温度T*。如图16(a),CeCoIn5在120 K时就可以观察到明显的重电子色散(f/d杂化),甚至杂化的起始温度可达270±30 K,而电阻率测量确定CeCoIn5的T*在50 K左右。类似的结果同样存在于其他研究组对CeCoIn5的共振光电子能谱温度依赖研究[36]。这种现象与早先的平均场图像的预期不一致。最近,杨义峰课题组通过计算认为在T*之上还存在相干杂化涨落,可能是上述实验结果的一个理论解释[86]。齐静波课题组通过超快光谱泵浦探测实验在CeCoIn5中观察到两个特征温标,分别对应传统电阻测量的相干温度T*和ARPES测得的能带弯折开始出现的温度T†(120 K),进一步证实在重费米子材料的T*之上可能的确存在杂化涨落现象[87]。
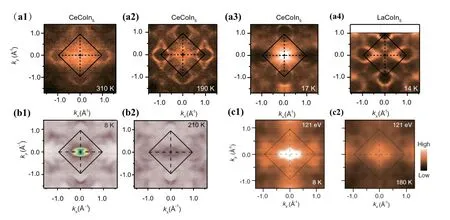
图18.CeMIn5费米面随温度的变化。(a)CeCoIn5和同构化合物LaCoIn5[50];(b)CeRhIn5[53];(c)CeIrIn5[52]。图中给出了测量温度。所有测量都是在共振光子能量(121 eV)下进行的。
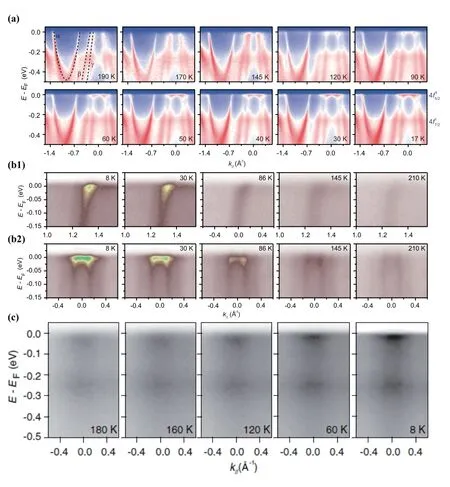
图19.CeMIn5沿Γ-M方向的4d→4f共振角分辨光电子谱随温度的变化。(a)CeCoIn5[50];(b)CeIrIn5[52];(c)CeRhIn5[53]。测量温度如图上所示。
研究者们定量的研究了费米能级附近4f电子谱重随温度的变化。如图20所示,(a)为从图19(c)中提取的CeRhIn5三个不同能带在费米跨越位置的不同温度下的能量分布曲线[53];(b)、(c)分别为从图19(a)、(b)中提取的CeCoIn5[50]、CeIrIn5[52]在Γ点附近的不同温度下的能量分布曲线;(d)显示了从图19中提取的三种材料费米能级附近的4f电子谱权重随温度的变化结果。从三者的能量分布曲线温度可以看到,近藤共振峰都在远高于相干温度的地方开始出现。值得注意的是CeRhIn5的三个不同能带费米跨越处的能量分布曲线(图20(a))展示出明显不同的温度变化关系,表明4f电子与导带电子杂化具显著的能带依赖性:对于组成二维费米面的α能带,f/d杂化强度较弱;具有最强kz色散的γ能带具有最强的杂化强度,与早期对CeCoIn5的能谱研究结果类似[47]。比较三种材料可以发现f电子谱权重随温度的降低增加的速率不一样(图20(d)),即f电子与导带电子杂化强度从高到低依次为CeIrIn5、CeCoIn5和CeRhIn5。
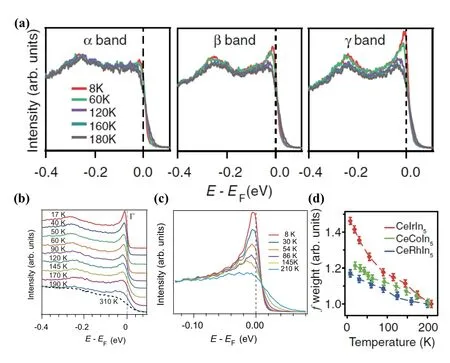
图20. CeMIn5能量分布曲线随温度的变化。(a)CeRhIn5的三条不同能带费米跨越位置处能量分布曲线[53]。(b)、(c)分别为从图16(a)、(b)中提取的CeCoIn5[50]和CeIrIn5[52]的Γ点附近的能量分布曲线。(d)CeCoIn5、CeRhIn5、CeIrIn5费米能级附近,f电子谱权重随温度的变化。积分自图15,能量范围为[EF-40 meV,EF+20 meV]。
3.CePt2In7
作为这一系列化合物中层间距离最大的化合物,CePt2In7的温度变化光电子能谱数据表现出了一些独特性[59]。图21为4d→4f共振条件下测得的Γ−M方向光电发射强度温度变化数据。从角积分谱变温度数据中(图21(e)),在温度低于60 K时在费米能级附近存在两个越来越明显的峰,分别标记为红色和黑色虚线,我们认为他们是来自于晶体场效应。如图21(f)所示,由图21(a)-(d)中不同动量积分宽度积分所得的f电子谱权重以及由85 eV测量的温度变化光电子能谱数据积分所得的费米能级附近的电子谱权重温度变化曲线表现出相同的温度变化趋势。自最高测量温度开始,谱权重开始是随温度的降低先增大后减小,极大值大概在60 K左右。这种非单调变化特征表明4f电子随温度降低是先变得更加巡游然后变得更加局域,与这一系列化合物其他成员的f电子谱权重温度变化是极为不同的,尽管其谱权重依然是在一个远高于其晶格相干温度的位置开始增加。这种更巡游到更局域的转变在对CePt2In7的奈特位移测量中也有体现,但是其转变温度为14 K,是远低于当前数据中的60 K的。注意到,在以前的光电导数据中在60 K处存在一个强的信号变化,而对CePt2In7的面内电阻率测量也表明一个特征温度范围40 K~80 K,再结合60 K左右晶体场劈裂态的出现,我们认为晶体场劈裂态的出现是与低温下4f复局域化的行为相关的,可能也是重费米子材料中重电子相干的前兆。然而关于这些过程是如何关联起来的,其详尽的物理过程还需要更多的实验和理论探索。

图21.(a)-(d)为CePt2In7沿Γ-M方向4d→4f共振(121 eV)ARPES从135 K到16 K的温度变化数据。(e)为对应温度下的角积分谱。(f)从(a)-(d)以及85 eV测量的温度变化光电子能谱数据(未展示)中提取的费米能级附近的f电子谱权重温度变化曲线[59,60]。
4.讨论
综上所述,对CemMnIn3m+2n系列材料的变温4d→4f共振ARPES谱实验探测到了明显的准粒子的产生过程及低温下的f电子的谱权重增强过程,发现在这一系列材料中电子结构随温度化具有以下特征:
1.目前,在所有费米面温度变化数据中,没有发现剧烈的由杂化引起的费米面体积变化;仅在Ce2RhIn8中发现了由涨落引起的费米面在高温时的塌缩现象。
2.大部分材料中f电子与导带电子的杂化可能在远高于相干温度T*的温度就已经开始,与通常所认为的杂化只在T*之下开始出现不符;此外,仅在Ce2IrIn8中发现近藤峰在温度高于T*之后消失。
3.对CeRhIn5的光电子能谱研究发现f/d杂化具有能带依赖性,三维性更强的能带与f能级的杂化更强,而相关理论计算也表明面外In原子的5p电子与Ce原子4f电子杂化更强。
4.在CeMIn5和Ce2MIn8系列材料中,f电子谱权重均自最高测量温度开始与温度呈负单调关系,即在远高于T*的温度开始随温度降低而增强,表明f电子在很高的温度就开始变得巡游。
5.对CePt2In7的变温研究发现f电子谱权重随温度先增强后减小的现象,且极大值位于T*附近,象征着f电子存在局域变得巡游在复局域化的过程,奈特位移测量结果也支持类似的过程,但转变温度存在差异;此外,CePt2In7中晶体场劈裂态也在T*附近开始变得明显,表明晶体场劈裂态激发可能与晶体相干温度、复局域化过程存在关联,但是详细的物理过程目前未知。
尽管温度变化的ARPES数据揭露了该系列材料电子结构中的许多信息,但是依然需要更多更高质量的实验数据。对不同温度下的各费米口袋总的大小的分析、温度变化过程中费米动量的改变大小(即f电子加入费米面的数量)的分析都需要高质量的费米面数据。在CeRhIn5和CePt2In7中,共振光电子能谱也并没有探测到清晰的杂化过程,这样阻碍了对实验数据做更多的定量分析。在CeCoIn5和CeIrIn5中,尽管观察到了比较明显的重准粒子的产生过程,但是许多小的费米口袋并不清晰,因此无法知道f电子加入各个费米口袋的情况。总之,对这系列材料的温度变化能谱研究需要进一步的定量化费米动量移动量随温度的变化关系,将有助于分析重费米子材料中f电子由高温下的全局域逐渐变得巡游的转变过程,从而更加准确地描述重费米子材料中的物理现象。同时,探索晶体场效应对重费米子杂化温度的影响,聚焦杂化温度之上的f电子的物理特征对理解重费米子物理都是极为重要的。
D.f电子与导带电子杂化
重费米子材料中,一般而言,随着f电子与导带电子的杂化强度逐渐增强,杂化能隙不断变大,对应着上下两支杂化能带之间的能量间隔增加,f电子平带也会具有一定强度的色散。实验上,在分析能谱数据的过程中可以通过使用方程(1)拟合测得的准粒子能带来得到杂化强度V。在实验数据能带结构不甚清晰的情况下,也可以通过杂化前后准粒子能带的能量移动大小ΔE在一定程度上反映该材料内的f/d杂化强度。本节中,总结了该系列材料中的ΔE和V,可以发现总体上这一系列材料中的杂化强度和能量移动都是小于20 meV,可见f/d杂化强度都是比较弱的,大部分的f电子都是局域的。
图22(a1)、(b1)分别为低温下CeIn3和CePt2In7中¯Γ−¯M方向上4d→4f共振价带结构[55,56]。通过比较不同动量位置处提取的能量分布曲线(图22(a2)、(b2)),可以发现在两种材料中4f态分别具有约4 meV、5 meV的色散,表明两者4f电子均具有较强的局域性且强度相近。早期对CeIrIn5的4d→4f共振ARPES实验表明其4f能带存在30 meV左右的色散[46],远高于CeIn3[55]和CePt2In7[56]。
如图23所示,(a)-(c)分别为CeCoIn5、CeIrIn5、CeRhIn5低温下¯Γ−¯M方向上4d→4f共振价带结构光电发射强度谱[53]。通过方程(1)的拟合,可以得到CeCoIn5与CeIrIn5中的杂化强度V分别为15±5 meV和18±5 meV,表明两者中CeIrIn5的杂化强度更强(如图(a3)、(b3))。通过同样的方式,同样发现Ce2PdIn8中的f/d杂化强度V~15±5 meV而4f态色散强度为6 meV,表明其杂化强度与CeCoIn5相当。
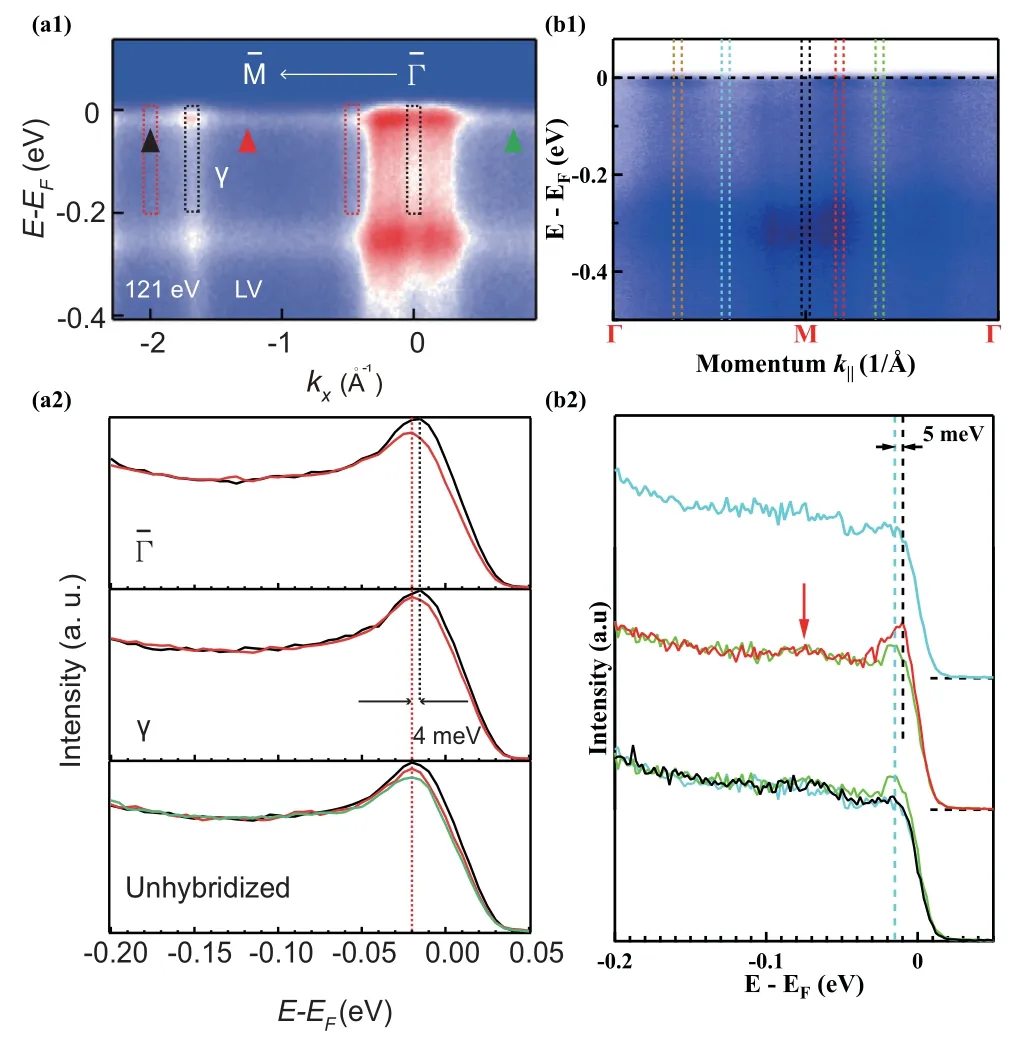
图22.(a)、(b)分别为CeIn3在13 K和CePt2In7在10 K下测得的-方向4d→4f共振价带结构((a1)、(b1))及不同动量位置处提取的能量分布曲线((a2))、((b2)),提取的动量位置如(a1)、(b1)中带色线框和线段所示[55-57]。
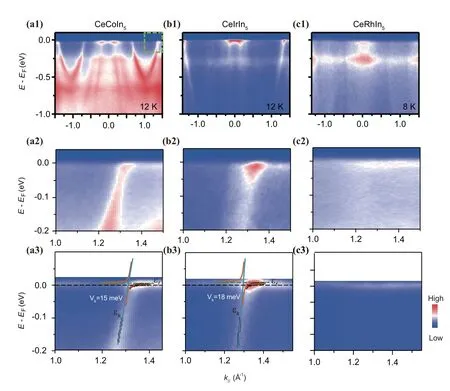
图23.(a)-(c)分别为CeCoIn5、CeRhIn5、CeIrIn5低温下-方向上4d→4f共振价带结构。(a2)、(b2)、(c2)分别为三者M点附近的能带杂化扩大图(如图(a1)青色方框所示)。(a3)、(b3)、(c3)分别为使用方程(1)对移除费米狄拉克函数和能量分辨率卷积处理后(a2)、(b2)、(c2)数据的拟合结果示[53,54]。
由以上数据可见,该类材料中化合物的f电子大部分依然是局域的。对这一系列材料的长期的光电子能谱研究也表明,这些材料中的能带结构往往与基于f电子为全局域的理论计算结果符合的较好,这说明所有化合物中只有少部分4f电子是巡游的。同时,比较分析可以知道,CeIn3和CePt2In7的4f电子可能具有较强的局域性,CeIrIn5中的4f电子则具有较强的巡游性,而CeCoIn5与Ce2PdIn8介于以上两者之间。基于以上结论,还可以发现这一系列材料中基态为超导态的材料往往具有较大的f/d杂化强度,而基态为磁有序态的材料杂化强度相对较小。
比较第二小节中对各材料近藤共振态的分析结果与本小节中各材料的杂化强度差异可以发现一些不一致的地方。通常,角积分谱中与峰强度之比和4f1与f0峰强度之比越大,往往意味着f电子巡游性越强即杂化强度越强。因此,基于第二小节的数据归纳可以知道,该系列材料中CeIn3具有最强的杂化强度,Ce2MIn8和CePt2In7具有最弱的杂化强度,CeMIn5介于两者之间。明显的,这一结果是与本小节中的结论不符的。因此,对该系列材料中f电子局域巡游性强弱的分析,需要更多更高质量的实验数据。所使用光子能量的体探测能力、数据的能量及动量分辨率等都会对分析结果造成影响。
IV.总结与展望
我们回顾了CemMnIn3m+2n系列化合物ARPES研究数据(包含部分光电子能谱数据),重点分析了各种材料中测得的费米面的拓扑特性、f电子与导带电子的杂化过程及近藤共振强度、4f电子的自旋轨道耦合强度及晶体场劈裂效应等问题,一些重要的结果和新奇的实验现象总结如下:
1.不同材料中的近藤共振态,4f自旋轨道耦合边带和4f0电离终态三者之间的强度比值存在明显的差异,反映的可能是f电子的局域巡游性强弱差异。在各材料中,CePt2In7具有最大的f电子自旋轨道耦合强度,Ce2MIn8系列化合物中的自旋轨道耦合强度最弱,但是各材料之间总体差别不大。
2.在部分材料中测量到了晶体场劈裂态,尽管实验数据并非特别直观。
3.对准粒子产生过程的变温光电子能谱研究发现了新的实验现象。首先,ARPES并没有在这一系列材料中观察到明显的由杂化引起的费米面体积随温度剧烈变化的实验结果,但是在Ce2RhIn8中发现了由涨落引起的高温时费米面的塌缩现象。其次,多种材料中观察到f/d杂化产生准粒子的过程发生在远高于T*的温度,与通常所认为的准粒子只在晶格相干温度以下形成的物理图像不符(尽管也在某些材料中发现T*以上近藤峰消失的现象),这一实验结果可能源于T*之上的杂化涨落。最后,在f/d杂化过程中,三维性更强的导带与f电子的杂化强度更大,这与面外In原子的5p电子同Ce原子4f电子杂化更强的理论计算结果一致[53]。
4.f电子谱权重随温度变化曲线在这一系列材料中呈现两种线形:在CeMIn5系列和大部分Ce2MIn8系列材料中,f电子谱权重自最高测量温度开始逐渐增强,意味着f电子在远高于T*的温度就开始变得巡游。在CePt2In7中,f电子谱权重随温度先增强,在T*之后开始减小,表明f电子在T*之下复局域化了;同时,晶体场劈裂态也在T*附近开始变得明显,这一现象表明f电子复局域化过程、晶格相干温度及晶体场劈裂激发态之间可能存在很强的内在联系,其背后的物理图像目前未知。
5.各材料中杂化强度差别显著,体现的是f电子的局域性和巡游性的差异。对于这一系列材料光电子能谱数据进行系统的收集和总结,将加深我们对现有实验结果的理解,为Ce基重费米子材料的理论模型完善提供最简单明了的实验结论,也为对这一系列材料的进一步研究提供指导。
除上文的总结的重要结果之外,我们也发现了一些新的问题。首先,作为一类典型的重费米子材料,其重准粒子能带在一般所认为的杂化温度之上就开始出现的物理原因究竟是杂化涨落还是存在其他的相互作用,这一点是需要更多的实验结果来论证的。其次,在f/d杂化开始在更高温度的条件下,对这类材料的光电子能谱数据依然没有探测到剧烈的费米面体积变化,而理论计算结果却表明是存在明显的大的变化的,因此对这类材料中f电子在不同温度下加入费米面的情况的研究依然是极为必要的。然后,对于这类材料的晶体电场劈裂态的观察是不充分的。现有的实验数据都需要做进一步的处理才能体现出晶体场劈裂态,而原始数据是不明显的,因此还需要更多高分辨率的实验数据。此外,如上文所述,在分析f/d杂化强度大小时,通过积分谱(或者能量分布曲线)中与峰强度之比和4f1与f0峰强度之比的大小与直接提取光电发射强度谱中f/d杂化强度V和重准粒子色散强度ΔE的大小所得结果是不一致的,而这一点同样是需要得到清晰解答的问题。最后,CeCoIn5是具有极高超导转变温度的重费米子材料,然而目前依然缺乏其超导转变温度之下的数据,因此也应该是下一阶段的实验目标;同时,CemMnIn3m+2n系列化合物中还有许多新发现的材料(如Ce3MIn11),对它们的研究既能与现有实验数据互相比较,或许也能带来更多新的实验结果。总之,针对以上总结的实验结果和未解决的问题,对这一系列材料进行进一步的能谱研究是非常必要的。
致谢
感谢国家自然科学基金(批准号:12074436,11574402)和中南大学创新驱动计划项目(项目号:2016CXS032)的支持。
