A survey of heavy-antiheavy hadronic molecules
2021-08-30DongXiangKunGuoFengKunZouBingSong
Dong Xiang-Kun Guo Feng-Kun Zou Bing-Song
1.CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190
2.School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049
3.School of Physics,Central South University,Changsha 410083
Abstract:Many efforts have been made to reveal the nature of the overabundant resonant structures observed by the worldwide experiments in the last two decades.Hadronic molecules attract special attention because many of these seemingly unconventional resonances are located close to the threshold of a pair of hadrons.To give an overall feature of the spectrum of hadronic molecules composed of a pair of heavy-antiheavy hadrons,namely,which pairs are possible to form molecular states,we take charmed hadrons for example to investigate the interaction between them and search for poles by solving the Bethe-Salpeter equation.We consider all possible combinations of hadron pairs of the S-wave singly-charmed mesons and baryons as well as the narrow P-wave charmed mesons.The interactions,which are assumed to be meson-exchange saturated,are described by constant contact terms which are resummed to generate poles.It turns out that if a system is attractive near threshold by the light meson exchange,there is a pole close to threshold corresponding to a bound state or a virtual state,depending on the strength of interaction and the cutoff.In total,229 molecular states are predicted.The observed near-threshold structures with hidden-charm,like the famous X(3872)and Pc states,fit into the spectrum we obtain.We also highlight a bound state that has a pole consistent with the cross section of the precisely measured by the BESIII Collaboration.
Key words:Hadronic molecules;exotic hadrons;hidden-charm systems;poles
CONTENTS
I.Introduction 66
II.Lagrangian from heavy quark spin symmetry 67
A.Heavy mesons 67
B.Heavy baryons 69
III.Potentials 71
A.Conventions 71
B.Potentials from light vector exchange 71
C.Potentials from vector charmonia exchange 72
IV.Molecular states from constant interactions 73
A.Poles 73
B.Discussions of selected systems 73
V.Summary and discussion 84
Acknowledgments 86
A.Vertex factors for direct processes 86
B.List of the potential factorF87
C.Amplitude calculation for cross processes 87
References 88
I.INTRODUCTION
The formation of hadrons from quarks and gluons is governed by quantum chromodynamics(QCD),which at low energy is nonperturbative.Therefore,it is difficult to tackle with the hadron spectrum modelindependently.The traditional quark model[1,2],where hadrons are classified as mesons,composed ofq¯qand baryons,composed ofqqq,provides quite satisfactory description of the hadrons observed in last century.The last two decades witnessed the emergence of plenty of states or resonant structures in experiments,many of which do not fit the hadron spectrum predicted by the naive quark model and thus are candidates of the socalled exotic states.Many efforts have been devoted to understand the nature of these states but most of them still remain controversial(see Refs.[3-18]for recent reviews).
The observation that most of these structures are located near the threshold of a pair of heavyantiheavy hadrons may shed light on identifying the nature of these structures.To name a few famous examples,let us mention theX(3872),akaχc1(3872)[19]andZc(3900)±[20-22]around thethreshold,theZc(4020)±[23,24]near thethreshold,theZb(10610)±andZb(10650)±[25,26]near theandthresholds,theZcs(3985)-[27]near theandDthresholds,and thePcstates[28]near thethresholds,respectively.These resonant structures were widely investigated in many models,including assigning them to be the molecular states of the corresponding systems.We refer to Ref.[8]for a comprehensive review of hadronic molecules.
Although these near-threshold resonant structures have been explored by many works using various methods,our understanding of these structures will greatly benefit from a whole and systematic spectrum of heavy-antiheavy hadronic molecules based on one single model.In this paper,we provide such a spectrum of hadronic molecules composed of a pair of heavyantiheavy hadrons includingS,P-wave heavy mesons andS-wave heavy baryons.The interactions between these hadron pairs are assumed to be contact terms saturated by meson exchanges as in,e.g.,Refs.[29-31].In order to have a unified treatment in all systems,we will not consider coupled-channel effects.In Ref.[31]a similar study,focusing on the possible bound states composed ofand,are performed.Also note that such interactions have been obtained in many other works,e.g.Refs.[32-37],to look for possible bound states associated with the near-threshold resonant structures.These works used different models and conventions and in some cases the results are inconsistent with each other.
In this work we consider the resonance saturation of the contact interaction due to the one-bosonexchange(light pseudoscalar and vector mesons)together with heavy quark spin symmetry(HQSS),chiral symmetry and SU(3)flavor symmetry,to estimate the potentials of the heavy-antiheavy systems,and special attention is paid to the signs of coupling constants to get self-consistent results.Heavy quark flavor symmetry(HQFS)implies that the potentials between bottomed hadron pairs are the same as those between charmed ones and thus we take charmed hadrons for example.The obtained potentials are used to solve the Bethe-Salpeter equation in the on-shell form to determine the pole positions of these heavy-antiheavy hadron systems and a systematic spectrum of these hadronic molecules is obtained.
Besides the possible molecular states,the interaction between a pair of heavy-antiheavy hadrons at threshold is crucial to understand the line shape of the invariant mass distribution of related channels,as discussed in Ref.[38].It is known that unitarity of theSmatrix requires the threshold to be a branch point of the scattering amplitude.Therefore,the square of amplitude modulus always shows a cusp at the threshold and a nontrivial structure may appear in the line shape of the invariant mass distribution.The detailed structure of the cusp,a peak,a dip or buried in the background,depends on the interaction of the two relevant particles near the threshold.More specifically,the cusp at the threshold of a heavy-antiheavy hadron pair will generally show up as a peak in the invariant mass distribution of a heavy quarkonium and light hadron(s),which couple to the heavy-antiheavy hadron pair,if the interaction is attractive at threshold and a nearby virtual state comes into existence(for subtlety and more detailed discussions,we refer to Ref.[38]).If the attraction is strong and a bound state is formed,the peak will be located at the mass of the bound state below threshold.Therefore,the potentials and the pole positions obtained in this work are of great significance for the study of near-threshold line shapes.
Note that the leading order interaction,which is just a constant,between a heavy-antiheavy hadron pair,when resummed,works well for both purposes mentioned above if we only focus on the near-threshold pole and line shape.Therefore,we only keep the leading order interaction,which is saturated by the vector meson exchange as discussed in the following,and its resummation.
This paper is organized as follows.In Section II,the Lagrangians of heavy hadron and light meson coupling are presented.In Section III,the potentials of different systems are obtained.We calculate the pole positions of different systems and compare them with experimental and other theoretical results in Section IV.Section V is devoted to a brief summary.Some details regarding the potentials are relegated to Appendices A,B and C.
II.LAGRANGIAN FROM HEAVY QUARK SPIN SYMMETRY
For hadrons containing one or more heavy quarks,additional symmetries emerge in the low energy effective field theory for QCD due to the large heavy quark mass[39,40].On the one hand,the strong suppression of the chromomagnetic interaction,which is proportional toσ·B/mQ~ΛQCD/mQwithΛQCD~200−300 MeV the typical QCD scale,implies that the spin of the heavy quarksQis decoupled with the angular momentumsℓof light quarks in the limit ofmQ→∞.Therefore,HQSS emerges,which means that the interaction is invariant under a transformation ofsQ.On the other hand,the change of the velocity of the heavy quark in a singly-heavy hadron during the interaction,Δv=Δp/mQ~ΛQCD/mQ,vanishes in the limit ofmQ→∞,and the heavy quark behaves like a static color source,independent of the quark flavor.Therefore,it is expected that the potentials between bottomed hadron pairs are the same as those of the charmed ones,and in turn it is sufficient to focus on the charm sector.
A.Heavy mesons
To construct a Lagrangian that is invariant under the heavy quark spin transformation and chiral transformation,it is convenient to represent the ground states of charmed mesons as the following superfield[41-43]
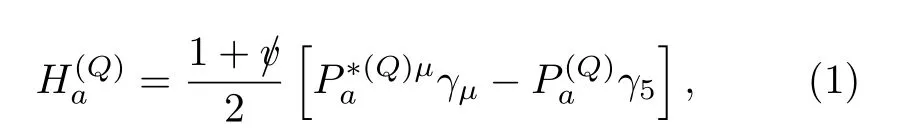
whereais the SU(3)flavor index,
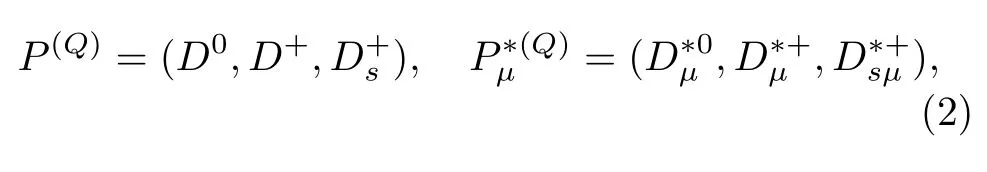
andvµ=pµ/Mis the four-velocity of the heavy meson satisfyingv·v=1.The heavy field operators contain a factorand have dimension 3/2.The superfield that creates heavy mesons is constructed as
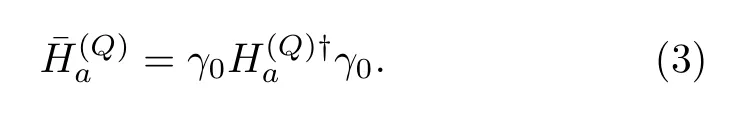
The superfields that annihilate or create mesons containing an antiheavy quark are notorbut the following ones[44]:
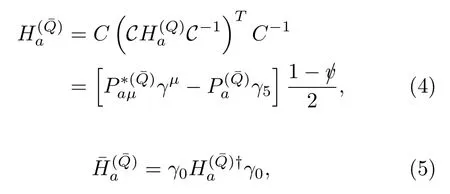
with

Cis the charge conjugation operator andC=iγ2γ0is the charge conjugation matrix,where we have taken the phase convention for charge conjugation asand.
TheP-wave heavy mesons have two spin multiplets,one withsℓ=1/2 represented bySwhile the other withsℓ=3/2 represented byT[45,46],
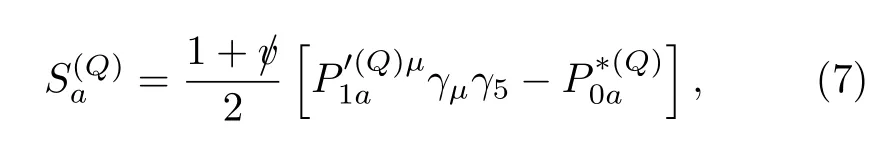
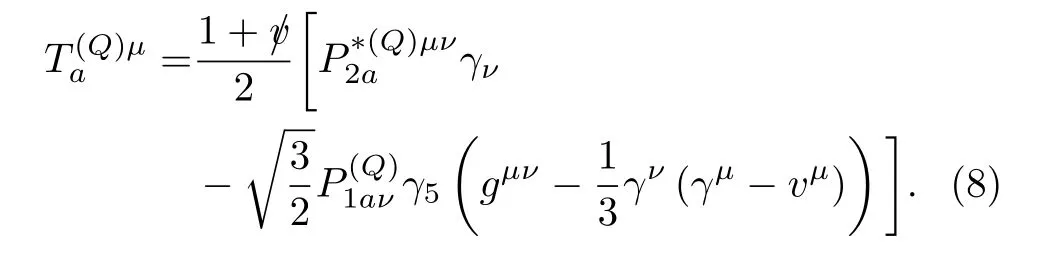
Analogous with Eqs.(3,4,5),we have
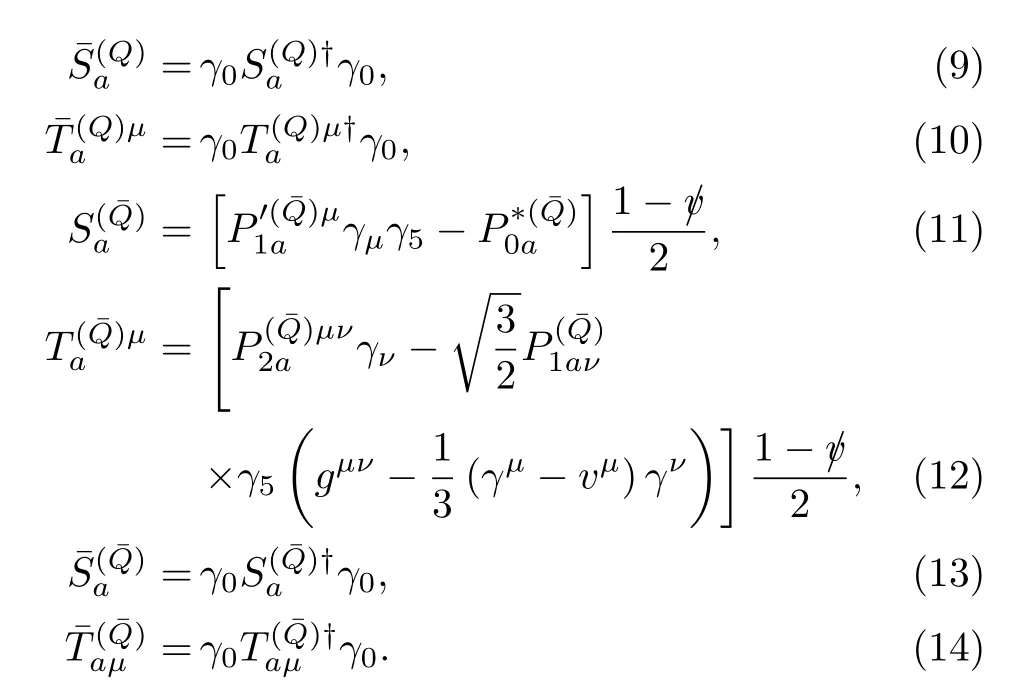
The mesons in theTmultiplet are
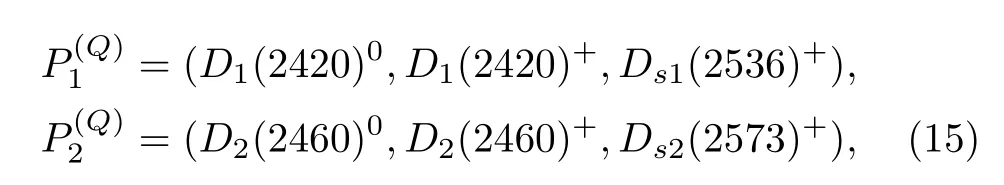
which can couple toD*π/Konly inD-wave in the heavy quark limit.While theP-wave charmed mesons withsℓ=1/2 can couple toD*π/KinS-wave without violating HQSS,there are issues in identifying them.The(2300)andD1(2430)listed in the Review of Particle Physics(RPP)[47]could be candidates for the charm-nonstrange ones.However,on the one hand,they have rather large widths such that they would have decayed before they can be bound together with another heavy hadron[48,49];on the other hand,they were extracted using the Breit-Wigner parameterization which has deficiencies in the current case[50]and has been demonstrated[51]to lead to resonance parameters for the(2300)in conflict with the precise LHCb data of theprocess[52].For the ones with strangeness,the lowest positive-parity(2317)andDs1(2460)are widely considered as molecular states ofDKandD*K[53-58],see Ref.[59]for a recent review collecting evidence for such an interpretation.This multipletS,therefore,will not be considered in the rest of this work.For studies of three-body hadronic molecular states involving the(2317)as aDKsubsystem,we refer to Refs.[60-63].
The light pseudoscalar meson octet can be introduced using the nonlinear realization of the spontaneous chiral symmetry breaking of QCD asΣ=ξ2andξ=withFπ=92 MeV the pion decay constant and
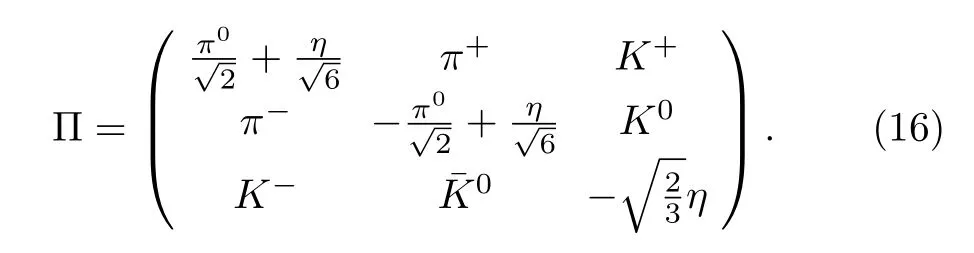
The effective Lagrangian for the coupling of heavy mesons and light pseudoscalar mesons is constructed by imposing invariance under both heavy quark spin transformation and chiral transformation[41,44,46],

whereDµ=∂µ+Vµ,D′µ=∂µ−Vµ,〈···〉denotes tracing over the Diracγmatrices,Λχ≃4πFπis the chiral symmetry breaking scale,and
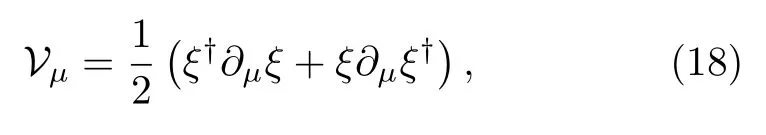

are the vector and axial currents which contain an even and odd number of pseudoscalar mesons,respectively.
The coupling of heavy mesons and light vector mesons can be introduced by using the hidden local symmetry approach[64-66],and the Lagrangian reads[42,43,67]
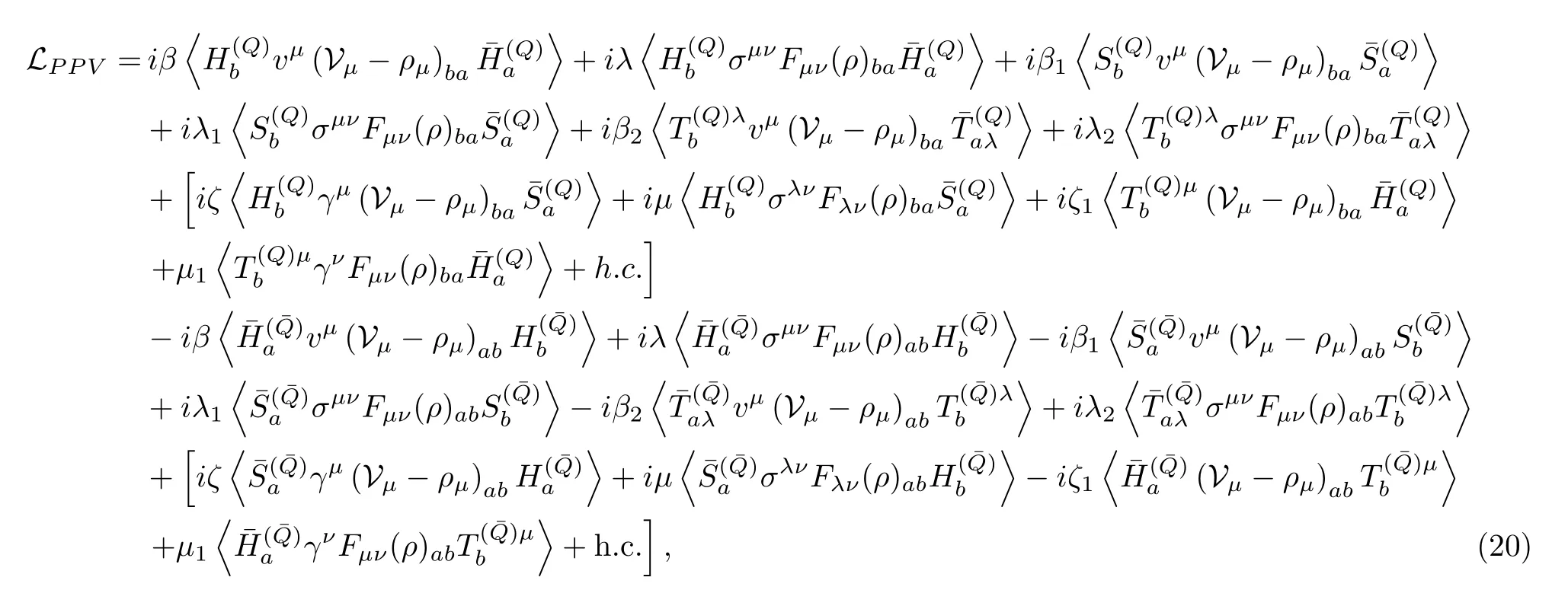
withFµν=∂µρν−∂νρµ+[ρµ,ρν],and
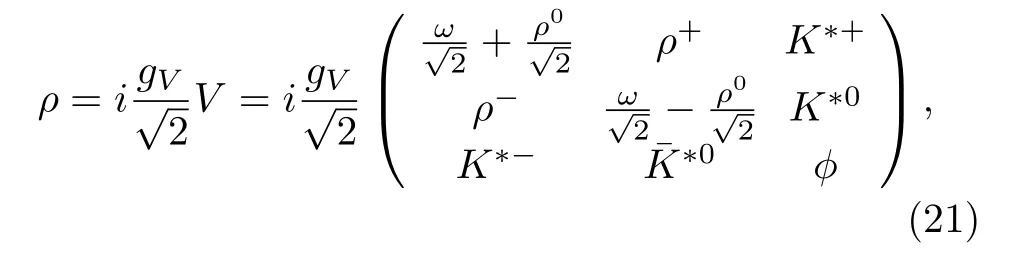
which satisfiesCV C-1=−V T.
Remind that in the following we are only interested in the potential near threshold and will not consider coupled channels.Therefore,the Lagrangian that results in potentials proportional to the transferred momentumq2will have little contributions.At the leading order of the chiral expansion,the light pseudoscalar mesons as Goldstone bosons only couple in derivatives,as demonstrated in Eq.(17),so all pseudoscalar exchanges have subleading contributions near threshold in comparison with the constant contact term that can generate a near-threshold pole after resummation.Moreover,coupled channels are not taken into account here,and we do not consider thesℓ=1/2 mesons.To this end we can just keep theβ,β2andζ1terms in Eq.(20).Expanding these terms we obtain
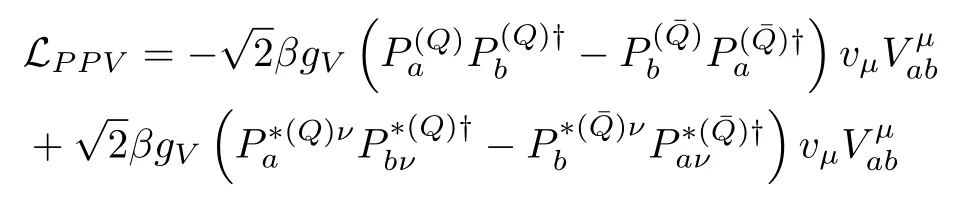
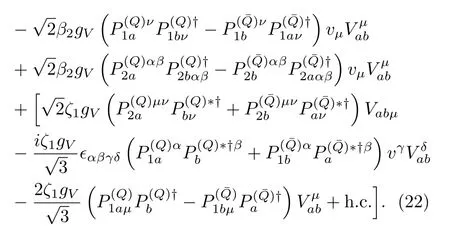
Assuming vector meson dominance,the coupling constantsgVandβwere estimated to be 5.8[65]and 0.9[68],respectively.In Ref.[69],it is estimated thatβ2≈−β=−0.9 under the assumption that the coupling ofD1D1Vis the same as that ofDDVandζ1≈0.16 from the decay ofK1→Kρ.
B.Heavy baryons
In the heavy quark limit,the ground states of heavy baryonsQqqform an SU(3)antitriplet withdenoted byand two degenerate sextets wit hdenoted by[70],

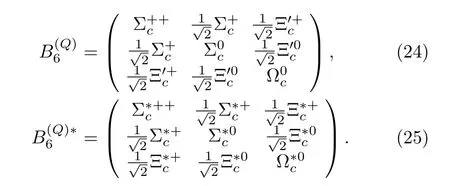
Here we do not consider theP-wave heavy baryons since they are not well established experimentally.The two sextets are collected into the superfieldSµ,
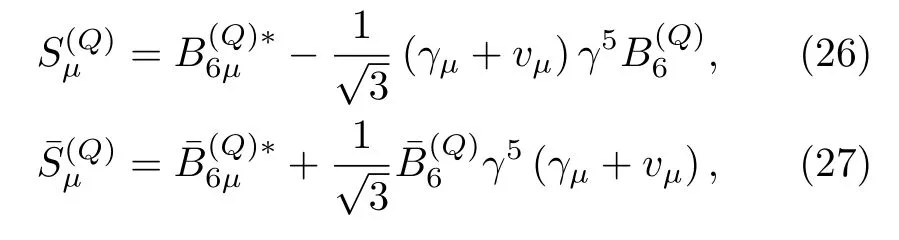
whereB6µis the Rarita-Schwinger vector-spinor field[71].The fields that annihilate anti-baryons are obtained by taking the charge conjugation ofand,
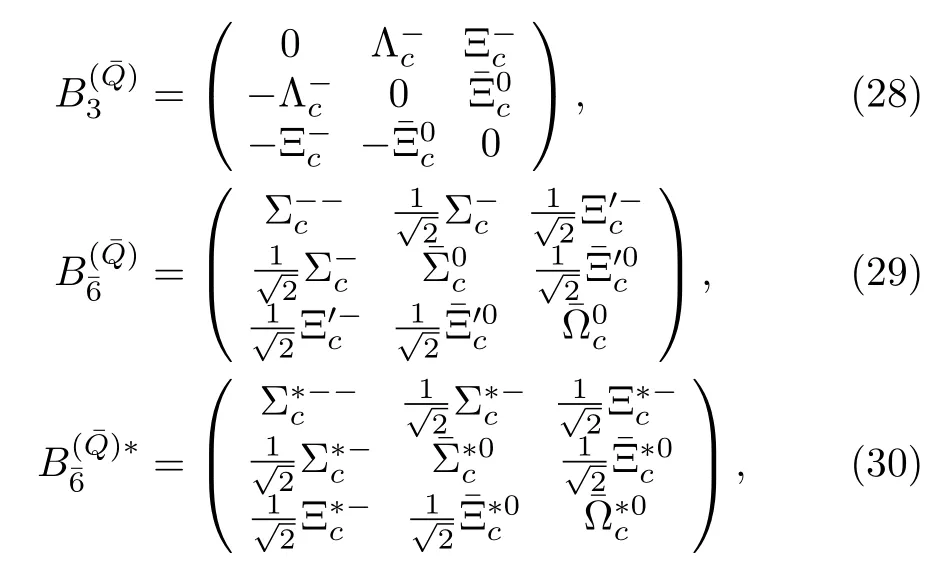
where we have used the phase conventions such that.The corresponding superfields now read
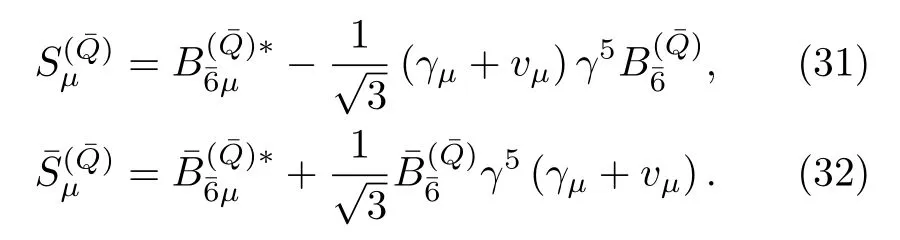
The Lagrangian for the coupling of heavy baryons and light mesons is constructed as[72]
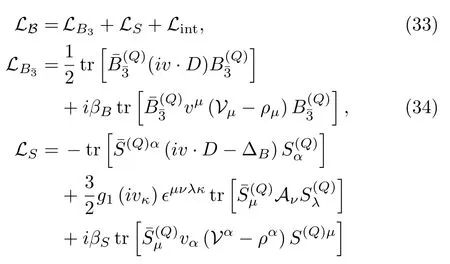
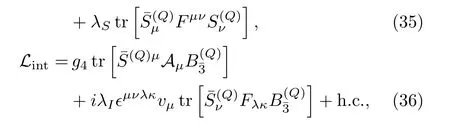
whereDµB=∂µB+VµB+,andΔB=m6−is the mass difference between the anti-triplet and sextet baryons.The coupling constantsβBandβSare estimated in Ref.[72]whereβS=−2βB=1.44 or 2.06 from quark model andβS=−2βB=1.74 from the vector meson dominance assumption.However,there is a sign ambiguity(only the absolute value of theρNNcoupling was determined from theNNscattering[73]).It turns out that the sign choice in Ref.[72]yields potentials of the anti-charmed meson and charmed baryon systems with an opposite sign compared to the ones obtained by SU(4)relations[35].It also conflicts with the famousPcstates[28],which are believed to be molecular states ofwith isospin 1/2—with a positiveβS,these systems will be repulsive(see below).These issues can be fixed by choosing the signs ofβBandβSopposite to those taken in Ref.[72],just like what Ref.[74]did.
For the coupling of antiheavy baryons and light mesons,by taking the charge conjugation transformation of the above ones,we have

with the transpose acting on the SU(3)flavor matrix.Notice that the spinor for an antibaryon isuinstead ofvsince here the fields of heavy baryons and heavy antibaryons are treated independently.
Similar with the Lagrangian for heavy mesons,we can focus on the vector exchange contributions,and only the following terms are relevant,
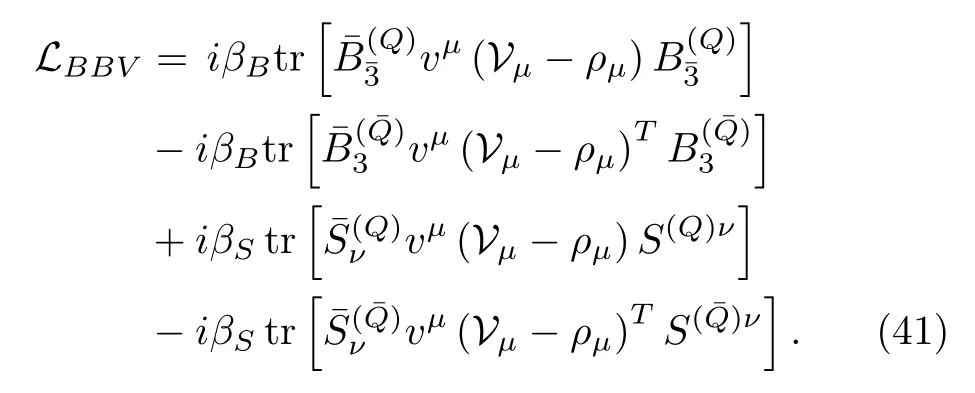
III.POTENTIALS
A.Conventions
In this paper,we take the following charge conjugation conventions:

which are consistent with the Lagrangians in Section II.Within these conventions,the flavor wave functions of the flavor-neutral systems that are charge conjugation eigenstates,including|DD*〉c,|DD1〉c,|D*D1〉c,|DD2〉c,|D*D2〉c,|D1D2〉cand,can be expressed as
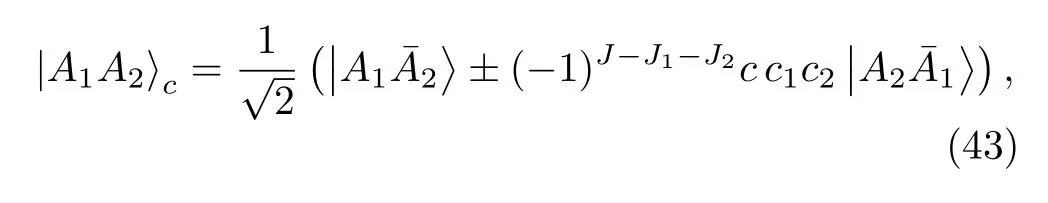
whereJiis the spin of|Ai〉,Jis the total spin of the system|A1A2〉c,ciis defined byC|Ai〉=,and the plus and minus between the two terms are for boson-boson and fermion-fermion systems,respectively.These systems satisfyC|A1A2〉c=c|A1A2〉cwithc=±1.
For the isospin conventions,we use the following ones:
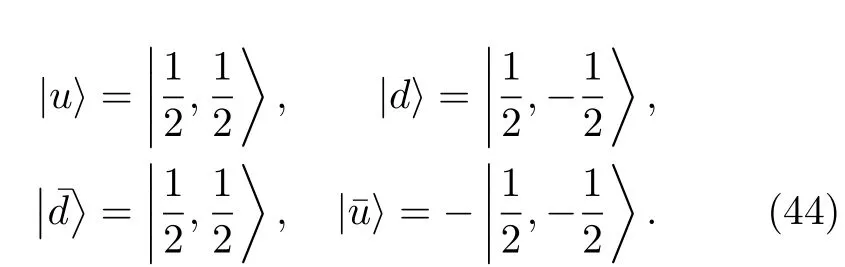
Consequently,we have
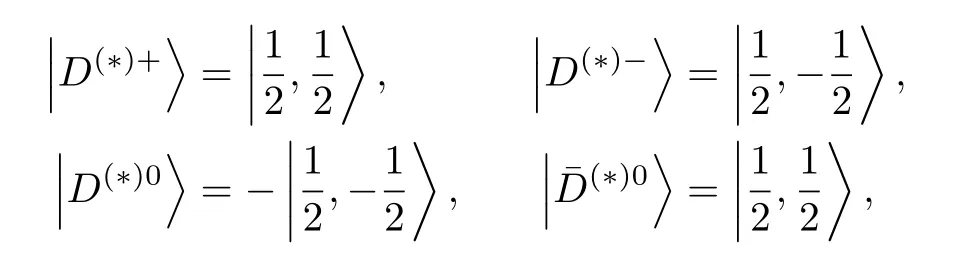
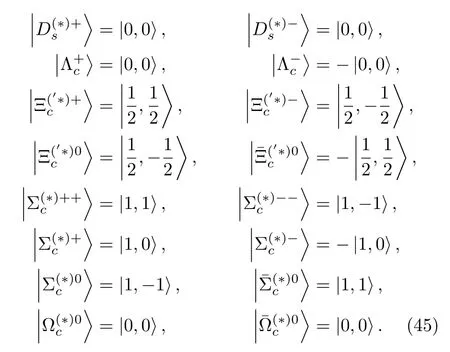
The isospin states ofD*,D1andare the same as those ofD.The flavor wave functions of the systems considered below with certain isospins can be easily computed using Clebsch-Gordan coefficients with these conventions.
The potential we calculate isV=−MwithMthe 2→2 invariant scattering amplitude so that a negativeVmeans an attraction interaction.This convention is the same as the widely used one in the on-shell Bethe-Salpeter equationT=V+V GT[75],and it is also the same as the nonrelativistic potential in the Schr¨odinger equation up to a mass factor.
B.Potentials from light vector exchange
With the Lagrangian and conventions presented above we are ready to calculate the potentials of different systems.We will use the resonance saturation model to get the approximate potentials as constant contact terms.Note that the resonance saturation has been known to be able to well approximate the low-energy constants(LECs)in the higher order Lagrangians of chiral perturbation theory[29,76],and it turns out therein that whenever vector mesons contribute they dominate the numerical values of the LECs at the scale around theρ-meson mass,which is called the modern version of vector meson dominance.
The general form ofMfor a processby the vector meson exchange reads
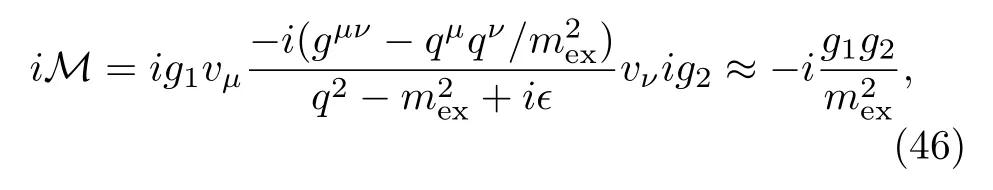
whereg1andg2account for the vertex information forA1and,respectively,q=p1−k1,and we have neglected terms suppressed by.For different particlesg1andg2are collected in Appendix A.It is worth mentioning that the spin information of the component particles is irrelevant here since the exchanged vectors only carry the momentum information,see Eqs.(22,41).Hence for a given system with different total spins,the potentials at threshold are the same.With the vertex factors evaluated,the potentials of different systems have a uniform expression,

wherem1,m2andmexare the masses of the two heavy hadrons and the exchanged particle,respectively.andare the coupling constants for the two heavy hadrons with the vector mesons,and,given explicitly,=βfor theS-wave charmed mesons,=−βfor theP-wave charmed mesons,=βBfor the anti-triplet baryons,and=−βS/2 for the sextet baryons.Fis a group theory factor accounting for the light-flavor SU(3)information,and in our convention a positiveFmeans an attractive interaction.The values ofFare listed in Tables VIII and IX in Appendix B for all combinations of heavy-antiheavy hadron pairs.
For a system which can have differentC-parities,like those in Eqs.(43),the potential is expressed as
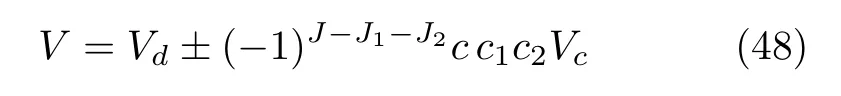
withVdthe potential from thedirectprocess,e.g.,andVcfrom thecrossone,e.g.,.Vd’s for these systems are covered by Eq.(47),
while for the cross processes,it turns out thatVc’s for|DD*〉c,|DD2〉c,|D1D2〉candsystems vanish at threshold.Explicit calculation shows that for the other three systems,|DD1〉c,|D*D1〉c,and|D*D2〉c,
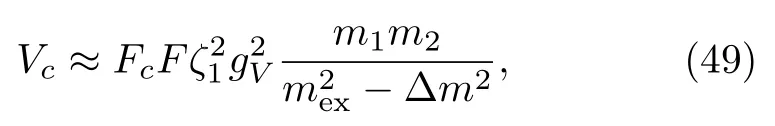
whereFis the same as in Eq.(47),Δm2=(m1−m2)2,and the additional factorFcaccounts for the spin information,which are shown in Appendix C.However,Vcis much smaller thanVdand has little influence on the pole positions compared with the cutoffdependence(see below).

TABLE I.Values of the coupling parameters used in the calculations.
In Table I,we collect the numerical values of the coupling parameters used in our calculations.
C.Potentials from vector charmonia exchange
In principle,theJ/ψ,as well as the excitedψvector charmonia,can also be exchanged between charmed and anti-charmed hadrons.Being vector mesons,their couplings to the charmed mesons have the same spinmomentum behavior as that of the light vectors.According to Eq.(47),such contributions should be suppressed due to the much larger masses of theψstates than those of the light vectors by a factor of~0.1,up to the difference of coupling constants.Therefore,the exchange of light mesons,if not vanishing,dominates the potentials at threshold.While for the systems where contributions from light vectors vanish(or theρandωexchanges cancel each other),the vector charmonia exchange,as the sub-leading term,will play an important role in the near-threshold potentials.
To be more precise,let us take theJ/ψexchange for example,for which the Lagrangian reads
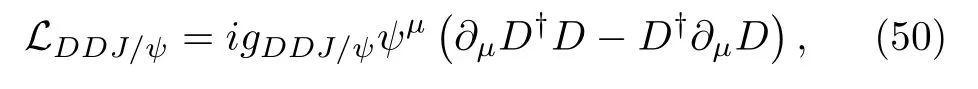
withgDDJ/ψ≈7.64[77].The resulting potential in the nonrelativistic limit is
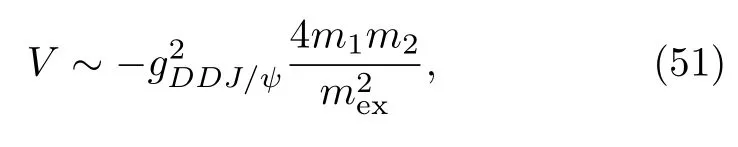
which is about 40%of the potential from theφexchange betweenDsand.The contributions from the other vector charmonia will be similar since their masses are of the same order.Notice that for all charmed and anti-charmed hadron systems,the vector charmonia exchange yields attractive interactions.Unfortunately,it is not easy to quantitatively estimate their contributions because the masses of these charmonia are much larger than the energy scale of interest,and there is no hierarchy among them to help selecting the dominant ones.Nevertheless,it could be possible to use,e.g.,theZc(3900),as a benchmark to estimate the overall contribution of the charmonia exchange.Given the controversy regarding its pole position[20,22,78-80],we refrain from doing so here(for further discussion,see Section IV.B.1).
IV.MOLECULAR STATES FROM CONSTANT INTERACTIONS
A.Poles
Now that we have obtained the constant interactions between a pair of heavy-antiheavy hadrons,we can give a rough picture of the spectrum of possible molecular states.We search for poles of the scattering amplitude by solving the single channel Bethe-Salpeter equation which factorizes into an algebraic equation for a constant potential,

whereGis the one loop two-body propagator.Here we adopt the dimensional regularization(DR)to regularize the loop integral[81],
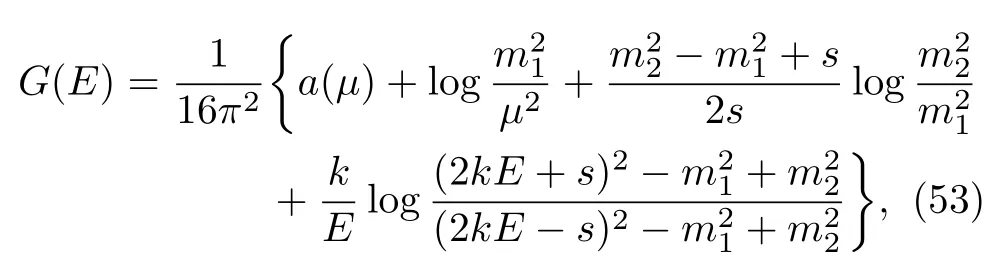
wheres=E2,m1andm2are the particle masses,and

is the corresponding three-momentum withλ(x,y,z)=x2+y2+z2−2xy−2yz−2xzfor the K¨all´en triangle function.Hereμ,chosen to be 1 GeV,denotes the DR scale,anda(μ)is a subtraction constant.The branch cut ofkfrom the threshold to infinity along the positive realEaxis splits the whole complex energy plane into two Riemann sheets(RSs)defined as Im(k)>0 on the first RS while Im(k)<0 on the second RS.Another way to regularize the loop integral is inserting a Gaussian form factor,namely,
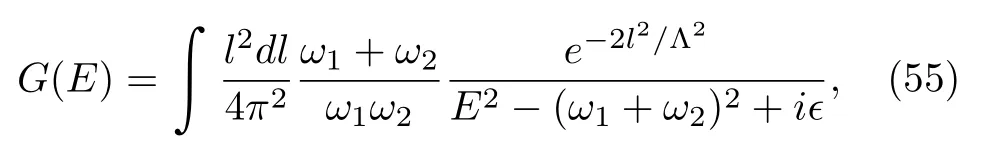
For a single channel,if the interaction is attractive and strong enough to form a bound state,the pole will be located below threshold on the first RS.If it is not strong enough,the pole will move onto the second RS as a virtual state,still below threshold.In Tables II,III,IV,V,VI and VII,we list all the pole positions of the heavy-antiheavy hadron systems which have attractive interactions,corresponding to the masses of hadronic molecules.For better illustration,these states,together with some hadronic molecule candidates observed in experiments,are also shown in Figs.1,2,3,4,5 and 6.In total,we obtain a spectrum of 229 hadronic molecules considering constant contact interactions,saturated by the light vector mesons,with the coupledchannel effects neglected.
B.Discussions of selected systems
It is worthwhile to notice that the overwhelming majority of the predicted spectrum is located in the energy region that has not been experimentally explored in detail.Searching for these states at BESIII,Belle-II,LHCb and other planned experiments will be important to establish a clear pattern of the hidden-charm states and to understand how QCD organizes the hadron spectrum.
In the following,we discuss a few interesting systems that have experimental candidates.
Within the mechanism considered here,the interactions ofandare the same.For the meson pairs to be isospin scalars,the attractions are strong enough to form bound states with similar binding energies,see Table II and Fig.2,while for the isovector pairs,the contributions from theρandωexchanges cancel each other,see Table VIII in Appendix B.

FIG.1.The spectrum of hadronic molecules consisting of a pair of charmed-anticharmed hadrons with(I,S)=(0,0).0--,1-+and 3-+are exotic quantum numbers.The colored rectangle,green for a bound state and orange for a virtual state,covers the range of the pole position for a given system with cutoffΛvaries in the range of[0.5,1.0]GeV.Thresholds are marked by dotted horizontal lines.The rectangle closest to,but below,the threshold corresponds to the hadronic molecule in that system.In some cases where the pole positions of two systems overlap,small rectangles are used with the left(right)one for the system with the higher(lower)threshold.The blue line(band)represents the center value(error)of the mass of the experimental candidate of the corresponding molecule.The averaged central value and error of theψ(4230)mass are taken from RPP[47].

FIG.2.The spectrum of hadronic molecules consisting of a pair of charmed-anticharmed hadrons with(I,S)=(0,0).2+-are exotic quantum numbers.The parameters of the X(3872)and˜X(3872)are taken from RPP[47]and Ref.[82],respectively.See the caption for Fig.1.
TheX(3872)observed by the Belle Collaboration[19]is widely suggested as an isoscalarmolecule withJPC=1++[84-87](for reviews,see,e.g.,Refs.[3,8,12,15]).Actually such a hadronic molecule was predicted 10 years before the discovery by T¨ornvist considering the one-pion exchange[88].Our results show that the light vector exchange leads to a nearthreshold isoscalar bound state that can be identified with theX(3872)as well,together with a negativeCparity partner ofX(3872)with the same binding energy(see also Refs.[89,90]).There is experimental evidence of such a negativeC-parity state,named as(3872),1It should be called hc(3872)according to the RPP nomenclature.reported by the COMPASS Collaboration[82].A recent study of themolecular states using the method of QCD sum rules also finds both 1++and 1+-states[91].
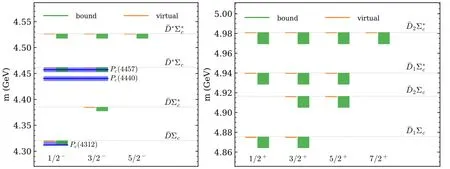
FIG.3.The spectrum of hadronic molecules consisting of a pair of charmed-anticharmed hadrons with(I,S)=(,0)and unit baryon number.The left orange band and right green band for each pole represent that the pole moves from a virtual state on the second RS to a bound state on the first RS when the cutoffΛchanges from 0.5 to 1.0 GeV.The parameters of these three Pc states are taken from Ref.[28],whose JP have not been determined experimentally.See the caption for Fig.1.
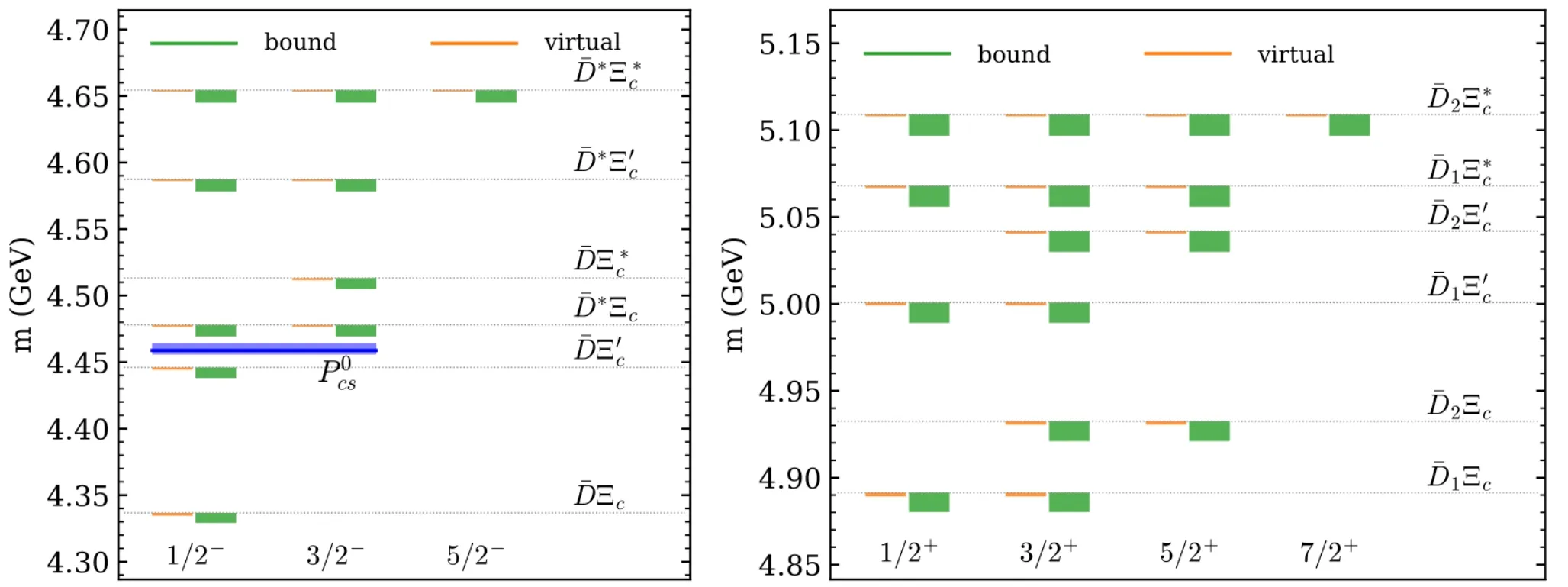
FIG.4.The spectrum of hadronic molecules consisting of a pair of charmed-anticharmed hadrons with(I,S)=(0,1)and unit baryon number.The parameters of Pcs(4459)are taken from Ref.[83],whose JP have not been determined experimentally.See the caption for Fig.3.
The potential predicting theX(3872)as an isoscalarbound state,also predicts the existence of isoscalarandbound states.By imposing only HQSS,there are two independent contact terms in theinteractions for each isospin[92,93],which can be defined as[8]
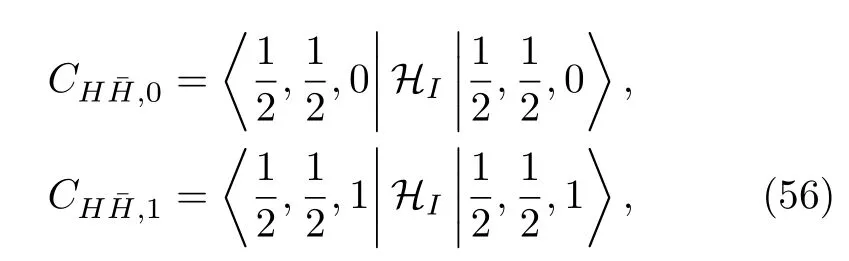
whereHIis the interaction Hamiltonian,and|sℓ1,sℓ2,sℓ〉denotes the charmed meson pair withsℓbeing the total angular momentum of the light degrees of freedom in the two-meson system andsℓ1,ℓ2for the individual mesons.Such an analysis leads to the prediction of a 2++tensor state as the HQSS partner of theX(3872)considering the physical charmed meson masses[93-95]and three partners with 0++,1+-and 2++in the strict heavy quark limit[96,97]that depend on the same contact term as theX(3872).The resonance saturation by the light vector mesons in fact leads to a relation,and consequently 6S-wavebound states.

FIG.5.The spectrum of hadronic molecules consisting of a pair of charmed-anticharmed hadrons with(I,S)=(1,0).See the caption for Fig.1.
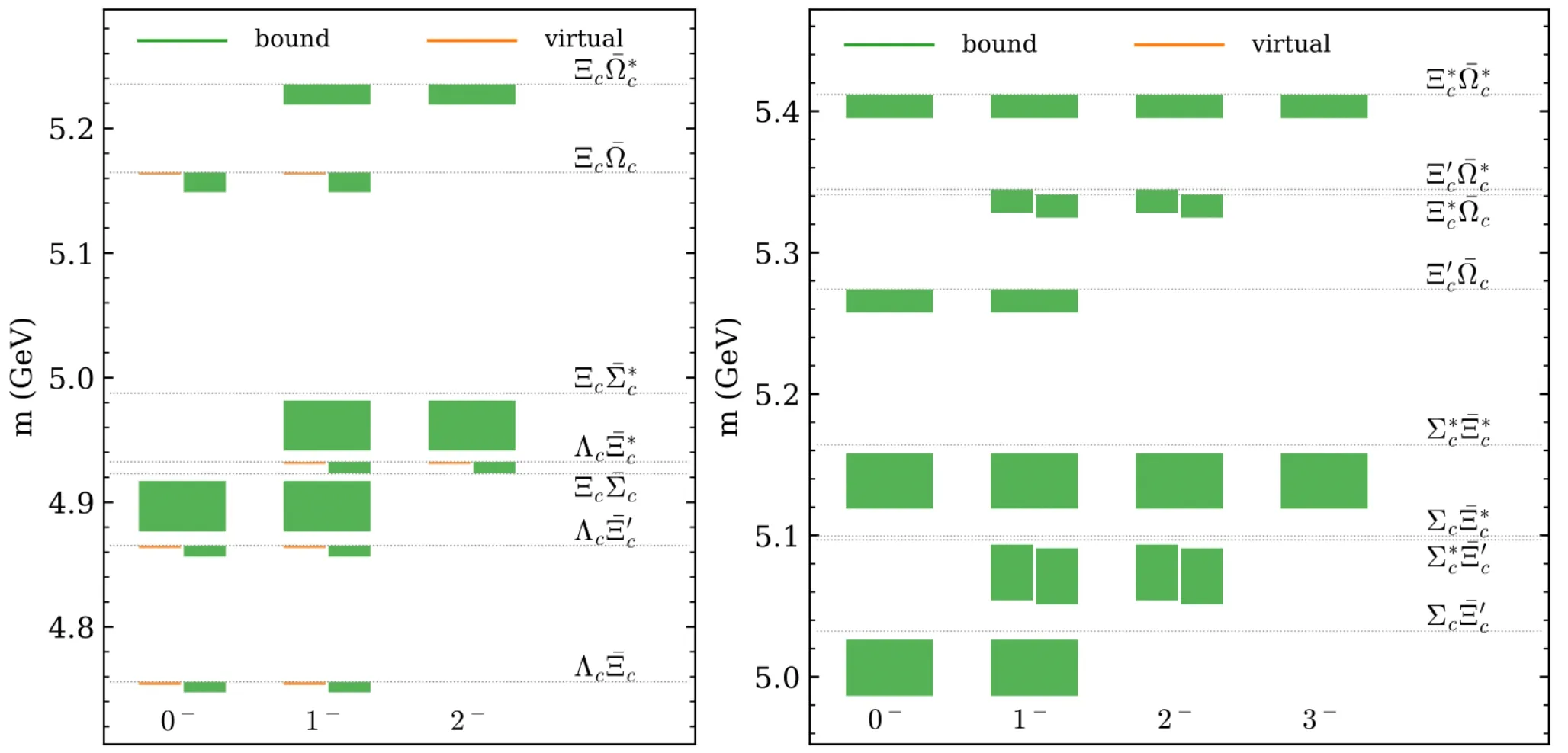
FIG.6.The spectrum of hadronic molecules consisting of a pair of charmed-anticharmed hadrons with(I,S)=(,1).See the captions for Figs.1 and 3.

TABLE II.Pole positions of heavy-antiheavy hadron systems with(I,S)=(0,0).Eth in the second column is the threshold in MeV.The number 0.5(1.0)in the third(fourth)column means that the cutoffΛ=0.5(1.0)GeV for Eq.(55)is used to determine the subtraction constant a(ω)in Eq.(53).In the last two columns,the first number in the parenthesis refers to the RS where the pole is located while the second number means the distance between the pole position and the corresponding threshold,namely,Eth-Epole,in MeV.
The existence of an isoscalarD¯Dbound state has been predicted by various phenomenology models[85,89,93,94,98,99],and more recently by lattice QCD calculations[100].Despite attempts[101-103]to dig out hints for such a state from the available experimental data[104-106],no clear evidence has yet been found.However,this could be because its mass is below thethreshold so that no easily detectable decay modes are available.
As for the isoscalar 2++bound state,it can decay intoD¯DinD-wave,and the width was predicted to be in the range from a few to dozens of MeV[97,107].
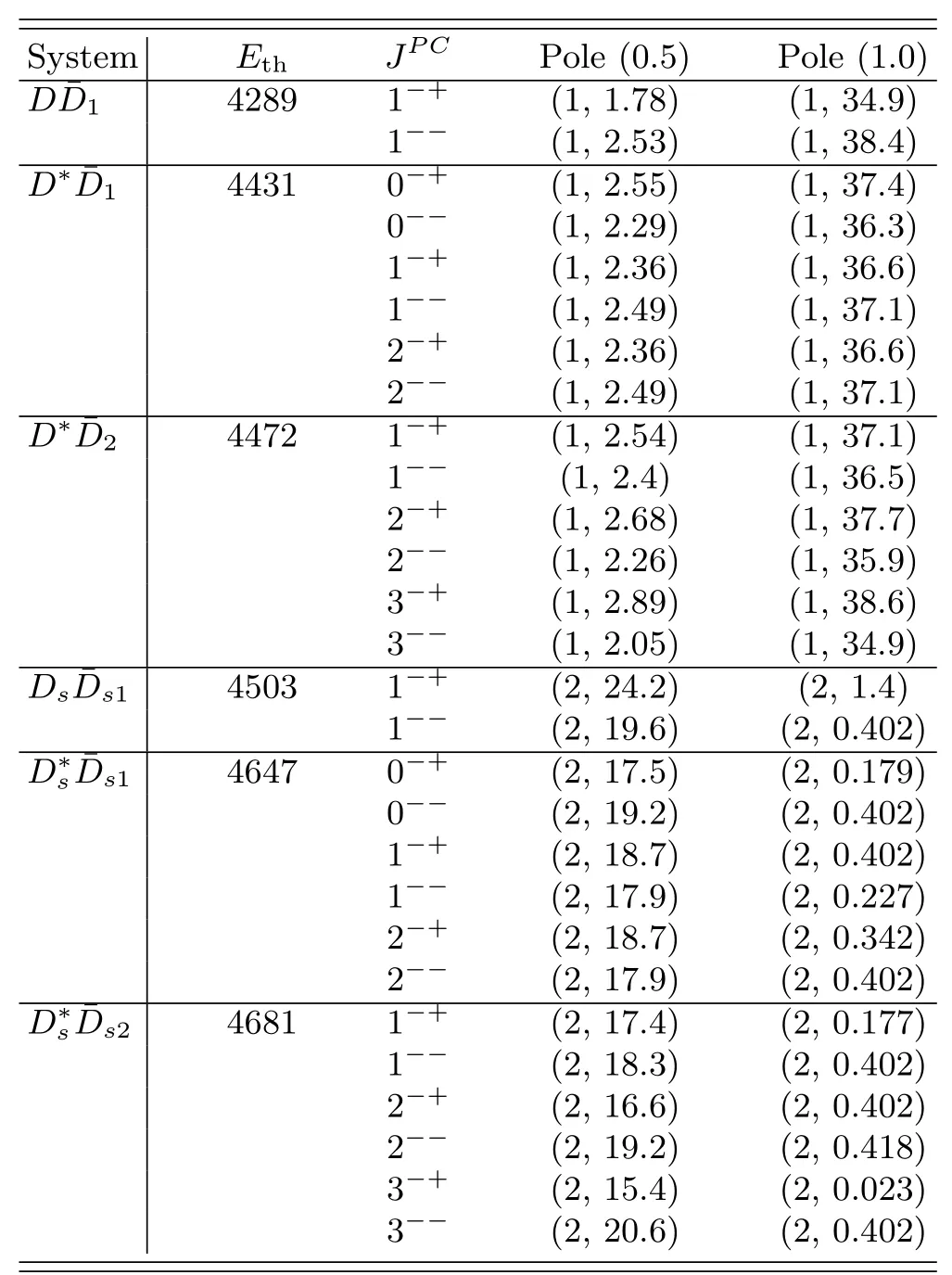
TABLE III.Pole positions of heavy-antiheavy hadron systems with(I,S)=(0,0).See the caption for Table II.In these systems different total spins and C-parities yield slightly different pole positions.

TABLE IV.Pole positions of heavy-antiheavy hadron systems with(I,S)=(1/2,0)and unit baryon number.See the caption for Table II.
No evidence has been found so far.One possible reason is that the coupling to ordinary charmonia could either move the 2++pole deep into the complex energy plane and thus invisible[108]2For a discussion of the intricate interplay between a mesonmeson channel with multiple quark model states,see Ref.[109].or make theinteraction in the 2++sector unbound[18,110].3Mixing of two energy levels will push them further apart.Thus,mixing of thestate with a lower-massχc2(2P)can effectively provide a repulsive contribution to theinteraction.For more discussions regarding the mixing of charmonia with mesonmeson channels,we refer to Refs.[111-113].

TABLE V.Pole positions of heavy-antiheavy hadron systems with(I,S)=(0,1)and unit baryon number.See the caption for Table II.
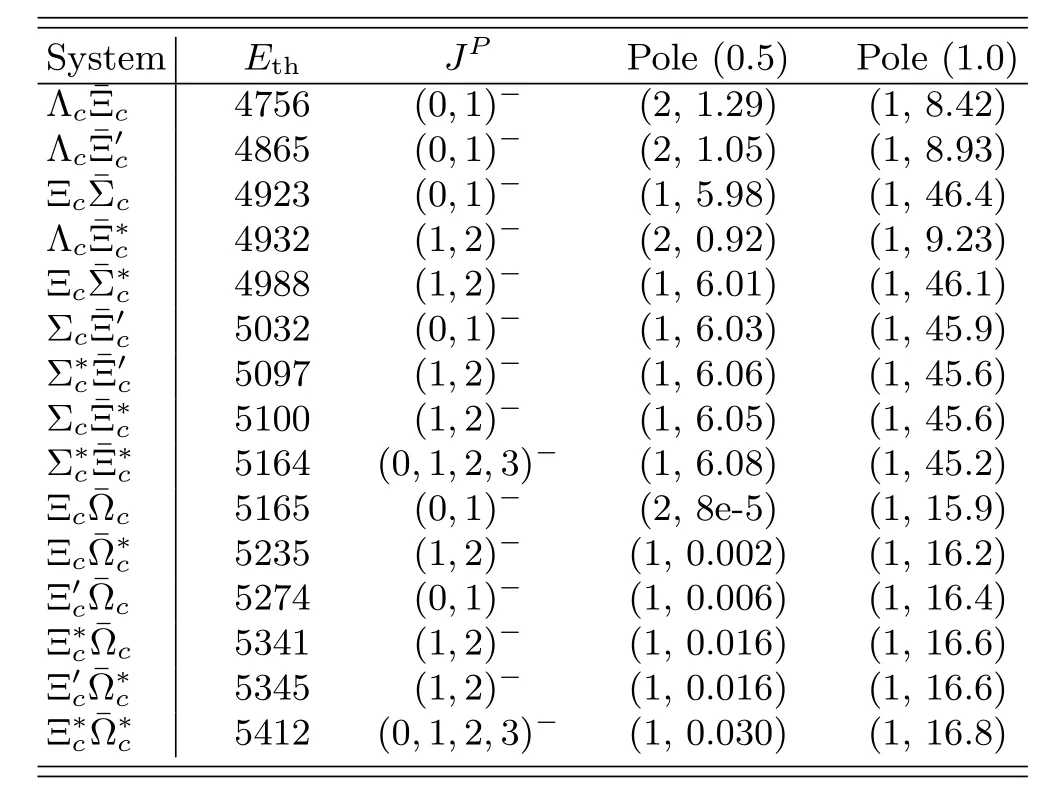
TABLE VI.Pole positions of heavy-antiheavy hadron systems with(I,S)=(1/2,1).See the caption for Table II.
TheZc(3900)[20-22]was also suggested to be an isovectormolecule with quantum numbersJPC=1+-[95,114]even though the light vector exchange vanishes in this case.Recall that the vector charmonia exchange will also yield an attractive interaction,as discussed in Section III.C,which can possibly lead to a virtual state below threshold.In fact,it has been suggested that theJ/ψ-exchange is essential in the formation of theZc(3900)in Ref.[115].It was shown in Refs.[78,116,117]that a virtual state assignment for theZc(3900)is consistent with the experimental data.4Notice that the coupling of the to a lower channel,which is J/ψπin this case,induces a finite width for the virtual state pole so that it behaves like a resonance,i.e.a pole in the complex plane offthe real axis.The same is true for all other poles generated here.Furthermore,it was shown in Ref.[118]that the finite volume energy levels are also consistent with the lattice QCD results which did not report an additional state[119].Similarly,theZc(4020)±[23,24]with isospin-1 near thethreshold can be a virtual state as well.It was recently argued that a near-threshold virtual state needs to be understood as a hadronic molecule[120].Analysis of the Belle data on theZbstates[25,26]using constant contact terms to construct the unitaryT-matrix also supports theZbstates as hadronic molecules[121-125].The molecular explanation of theZcandZbstates is further supported by their decay patterns studied using a quark exchange model[126,127].Without a quantitative calculation,as commented in Section III.C,we postulate that there can be 6 isovector hadronic molecules(with the sameJPCas the isoscalar ones)as virtual states of,which will show up as prominent threshold cusps(see Ref.[38]for a general discussion of the line shape behavior in the near-threshold region).
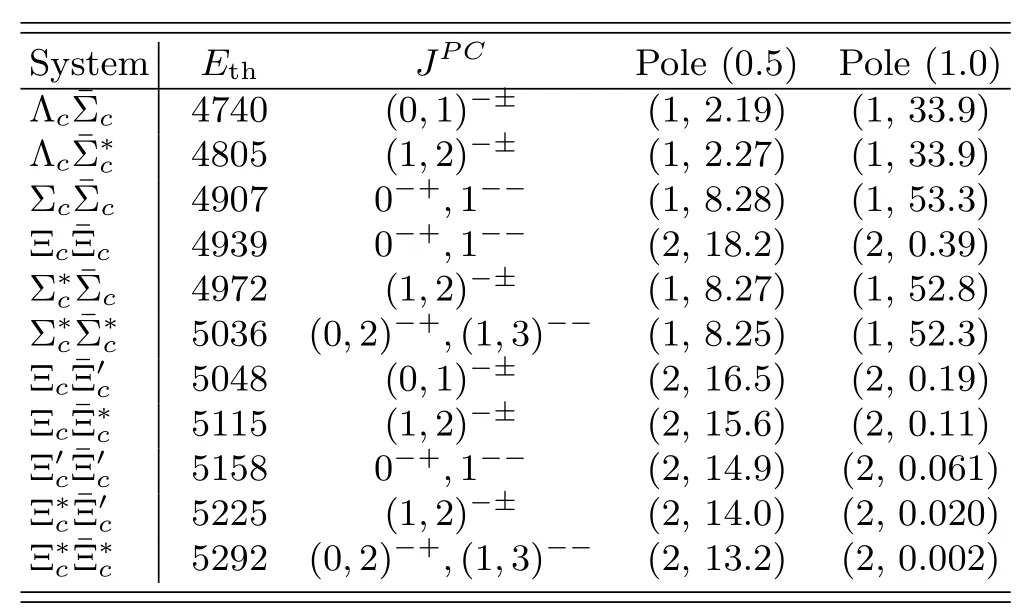
TABLE VII.Pole positions of heavy-antiheavy hadron systems with(I,S)=(1,0).See the caption for Table II.
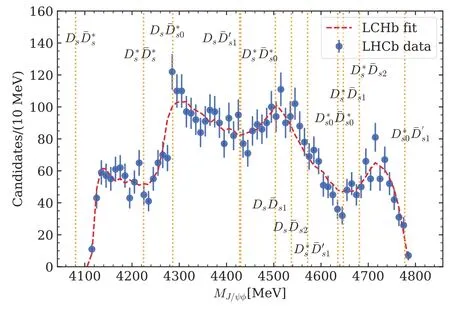
FIG.7.Thresholds of charm-strange meson pairs in the energy range relevant for the B+→J/ψφK+.Here,denotes (2317),Ds1 and D′s1 denote Ds1(2536)and Ds1(2460),respectively,and Ds2 denotes Ds2(2573).The data are taken from Ref.[131].
Here we find that the potential from theφexchange is probably not enough to form bound states of.Instead,virtual states are obtained,see Table II and Fig.2.
On the contrary,based on two prerequisites that
1.X(3872)is a marginally bound state ofwith binding energy 0~1 MeV,and
TheX(4140)first observed by the CDF Collaboration[132]was considered as a molecule ofwithJPC=0++or 2++in Refs.[33,133-138],which is,however,disfavored by the results of LHCb[131,139]where theJPCofX(4140)were suggested to be 1++(and thus theX(4140)was named asχc1(4140)in the latest version of RPP).Actually in our calculation,it is not likely for theto form such a deeply bound state,noticing that theX(4140)is about 80 MeV below the threshold of.Instead,it is interesting to notice that just at thethreshold there is evidence for a peak in the invariant mass distribution ofJ/ψφ,see Fig.7.5This structure around the threshold drew the attention of Ref.[140]where two resonances,a narrow X(4140)and a broad X(4160),were introduced to fit the J/ψφinvariant mass distribution from the threshold to about 4250 MeV.There the broad X(4160)was considered as a molecule.Following the analysis in Ref.[38],if the interaction of theis attractive but not strong enough to form a bound state,a peak will appear just at thethreshold in the invariant mass distribution ofJ/ψφ,and the peak is narrow if there is a nearby virtual state pole.A detailed study of this threshold structure can tell us whether the attraction between a pair of charm-strange mesons is strong enough to form a bound state or not.
The difference between theJ/ψφandthresholds is merely 36 MeV.Thus,the shallowvirtual state with 1++could be responsible for the quick rise of theJ/ψφinvariant mass distribution just above threshold observed in the LHCb data[131].
No light vector can be exchanged here and the attractive interaction from vector charmonia exchange is crucial,similar to the isovectorsystems.A virtual state pole could exist below threshold.In particular,if theZc(3900)exists as a virtual state,the same interaction would inducevirtual states.
Recently,a near-threshold enhancement in the invariant mass distribution ofwas reported by the BESIII Collaboration[27]and an exotic stateZcs(3985)-was claimed.This state has been widely investigated[141-158],some of which regard it as a molecule ofwhile some others object such an explanation.In Ref.[145],it was found that a virtual or resonant pole together with a triangle singularity can well reproduce the line shape of the BESIII data,consistent with the analysis here.
It is possible for the isoscalarpair to form a bound state with a binding energy from a few MeV to dozens of MeV.Note that this system can haveJPC=1-±and the 1--state is slightly more deeply bound than the 1-+one which has exotic quantum numbers.
TheY(4260)was discovered by theBABARCollaboration[159]with a mass of(4259±)MeV and a width of 50~90 MeV and later confirmed by other experiments[160,161].Now it is calledψ(4230)due to a lower mass from the more precise BESIII data and a combined analysis in four channels,,π+π-hc[163],π+π-J/ψ[164]andD0D*-π++c.c.[165],yielding a mass of(4219.6±3.3±5.1)MeV and a width of(56.0±3.6±6.9)MeV[166].This state is a good candidate of exotic states(see reviews,e.g.,Refs.[3,8,19]).It was argued that the isoscalarplays important roles in the structure ofY(4260)in,e.g.,Refs.[114,167,168].The binding energy of the isoscalarsystem withJPC=1-±via the vector meson exchange was calculated by solving the Schr¨odinger equation in spatial space in Ref.[69],and the results are consistent with this work except that the sign ofVc,which has a minor impact,is not correct there.Note that the mass of the isoscalarbound state obtained here is larger than the nominally mass of theψ(4230),see Fig.1,but the mixing of themolecule with aD-wave vector charmonium[169]may solve this discrepancy.
From the results in Table II and Fig.1,the isoscalarbound state has quite some partners,either of HQSS or of SU(3)flavor.In particular,several of them have vector quantum numbers,including abound state with a mass about 4.39~4.43 GeV,abound state with a mass about 4.43~4.47 GeV,and three virtual states ofand.
The current status of the vector charmonium spectrum around 4.4 GeV is not clear,and the peak structures in exclusive and inclusiveR-value measurements are different(for a compilation of the relevant data,see Ref.[170]).Thus,it is unclear which structure(s)can be identified as the candidate(s)of thebound states.Nevertheless,theY(4360),akaψ(4360),andψ(4415)have been suggested to correspond to theandstates,respectively[171-174].A determination of the poles around 4.4 GeV would require a thorough analysis of the full data sets including these open-charm channels,and the first steps have been done in Refs.[175,176].
As for the virtual states with hidden-strangeness,they are expected to show up as narrow threshold cusps in final states likeJ/ψf0(980)andψ(2S)f0(980).They could play an important role in generating theY(4660),akaψ(4660),peak observed in theψ(2S)f0(980)→ψ(2S)π+π-invariant mass distribution[177,178].6The Y(4660)was suggested to be aψ(2S)f0(980)bound state in Ref.[179]to explain why it was seen only theψ(2S)π+πfinal state with the pion pair coming from the f0(980).Although it was proposed[180,181]that theY(4630)structure observed in thespectrum[182]could be the same state as theY(4660)one,the much more precise BESIII data[183],however,show a different behavior up to 4.6 GeV in theinvariant mass distribution(see below).Further complications come from the 1--structures around 4.63 GeV reported in the+c.c.[184]and+c.c.[185]distributions,the former of which has been proposed to be due to a molecular state from theinteraction[186].Suffice it to say that the situation of theY(4630)is not unambiguous.With more precise data that will be collected at BESIII and Belle-II,we suggest to search for line shape irregularities(either peaks or dips)at theandthresholds in open-charm-strangeness final states such asand.
There are also hints in data for positiveCparityandvirtual states(see Table III and Fig.1),whose thresholds are at 4503 MeV and 4647 MeV,respectively.As can be seen from Fig.7,there is a peak around 4.51 GeV and a dip around 4.65 GeV in theJ/ψφenergy distribution measured by the LHCb Collaboration[131],and the energy difference between the dip and peak approximately equals to the mass splitting between theandDs.We also notice that the highest peak in the same data appears at thethreshold.7The coincidence of the peak position with the threshold and the highly asymmetric line shape suggests a virtual state.Such systems will be studied in a future work.All these channels,together with theanddiscussed in Section IV.B.2,need to be considered in a reliable analysis of theB+→J/ψφK+data,which is however beyond the scope of this paper.
Notice that because theD1(2)andDs1(s2)have fi- nite widths,the molecular states containing one of them can decay easily through the decays ofD1(2)orDs1(s2).The structures at the thresholds of,for which virtual states are predicted,will get smeared by the widths ofDs1(s2).Thus,thethreshold structures should be broader and smoother than theones since the width of theDs2,(16.9±0.7)MeV[47],is much larger than that of theDs1,(0.92±0.05)MeV[47].
5.Λc¯Λc:analysis of the BESIII data and more baryon-antibaryon bound states
From Table II and Fig.1,in the spectrum of the isoscalar 1--states,in addition to those made of a pair of charmed mesons,we predict more than 10 baryonantibaryon molecules.The lowest one is theΛc¯Λcbound state,and the others are above 4.85 GeV.While those above 4.85 GeV are beyond the current reach of BESIII(there is a BESIII data-taking plan in the energy region above 4.6 GeV[187]),there is strong evidence for the existence of aΛc¯Λcbound state in the BESIII data[183].
The cross section ofe+e-→was first measured using the initial state radiation by Belle[182]and a vector charmonium-like structureY(4630)was observed.The BESIII Collaboration measured such cross sections at four energy points just above threshold much more precisely[183].The energy dependence of the cross sections at these four points has a weird behavior:it is almost flat.This can be understood as the consequence of the Sommerfeld factor,which makes the distribution nonvanishing even exactly at threshold,and the existence of a near-threshold pole,which counteracts the increasing trend of the phase space multiplied by the Sommerfeld factor to result in an almost flat distribution.Here we fit BESIII data to estimate where the pole is located.
The Sommerfeld factor[188]accounting for the multi-photon exchange between theandreads,
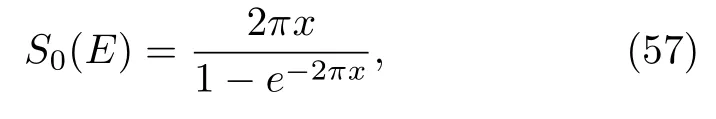
wherex=αμ/kwithα≈1/137,μ=mΛc/2,andkis defined in Eq.(54).The cross section ofe+e-→Λc¯Λcis now parameterized as
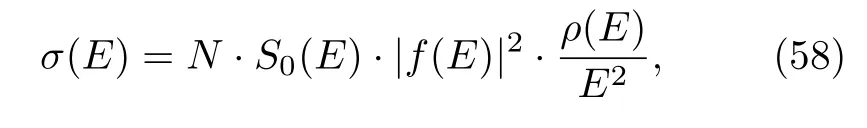
withNa normalization constant andρ(E)=k/(8πE)the phase space.Heref(E)denotes the nonrelativistic scattering amplitude,and theS-wave one,
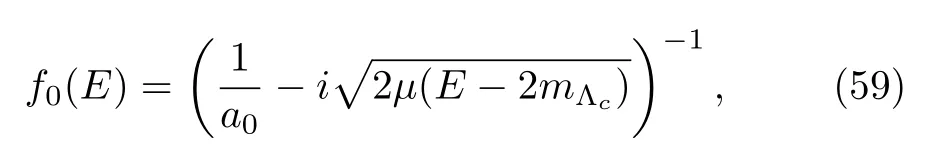
is sufficient in the immediate vicinity of the threshold.Note that we take the scattering lengtha0complex to take into account the couplings between theand lower channels[54].Finally,we have 3 parameters,Re(1/a0),Im(1/a0)andN,to fit four experimental data.
The fitted results are shown in Fig.8.We can see that the best fit leads to a pole located close to the real axis but above threshold.A pole below threshold,as we predicted,is also possible,see the bottom one in Fig.8.These fits,though with largerχ2,are reasonable since we have only four points.The obtaineda0values from these fits yield poles several MeV below threshold with an imaginary part of dozens of MeV.Such poles are located on the first RS corresponding to a bound state,which moves from the real axis onto the complex plane due to the coupling to lower channels.There is another pole located at the symmetric position on the second RS,corresponding to a virtual state.Actually,with the scattering length approximation in Eq.(59),we cannot determine on which RS the pole is located since the poles on different RSs below threshold have the same behavior above threshold.More data are needed to pin down the exact pole position corresponding to our predictedbound state,which should be different from theY(4630)orY(4660).In Ref.[189],the BESIII[183]and Belle[182]data are fitted together using an amplitude with a pole around 4.65 GeV.While the Belle data of theY(4630)peak can be well described,the much more precise BESIII data points in the near-threshold region cannot.We conclude that the data fromthreshold up to 4.7 GeV should contain signals of at least two states:themolecule and another one with a mass around 4.65 GeV.
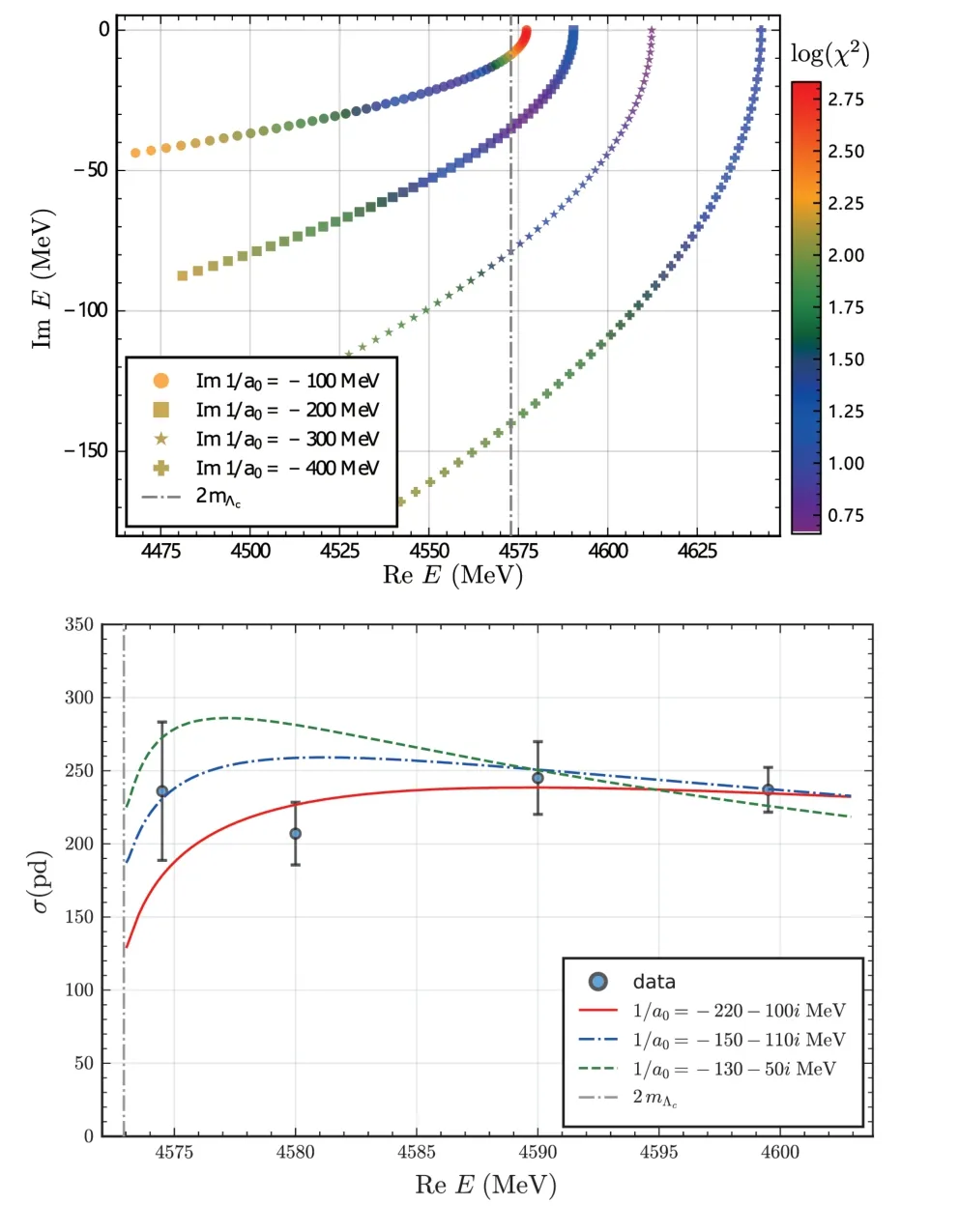
FIG.8.Top:pole positions of Eq.(59)on the first RS with different scattering length(a0)values and the color represents theχ2(in a logarithmic form for better illustration)of the fit to BESIII data[183].The pole on the second RS is at the same position if we change the sign of Re(1/a0),which does not change the fit.Bottom:examples of some fits,which yield poles below threshold at 4456-19i MeV(red),4468-14i MeV(blue dash-dotted)and 4566-6i MeV(green dashed).
As for the isoscalar vector states above 4.85 GeV,the structures could be more easily identified from data than those around 4.3 GeV.This is because the charmonium states in that mass region should be very broad while these hadronic molecules are narrower due to the small binding energies,corresponding to large spatial extensions.We expect theandbelow 5 GeV to be seen in the forthcoming BESIII measurements,and the ones higher than 5 GeV can be searched for in future super tau-charm facilities[190,191].
There are isovector 1--baryon-antibaryon molecular states above 4.7 GeV,see Table VII and Fig.5.It is more difficult to observe these states than the isoscalar ones ine+e-collisions since the main production mechanism of vector states should be driven by a vectorγµccurrent,which is an isoscalar,coupled to the virtual photon.However,they could be produced together with a pion,and thus can be searched for in future super tau-charm facilities with center-ofmass energies above 5 GeV.
Such systems have drawn lots of attention[34-36,192-196]especially after the pentaquark states,Pc(4450)andPc(4380),were observed by LHCb[197].In the updated measurement[28],thePc(4450)signal splits into two narrower peaks,Pc(4440)andPc(4457).There is no clear evidence for the previous broadPc(4380),and meanwhile a new narrow resonancePc(4312)shows up.Several models have been applied by tremendous works to understand the structures of these states,and themolecular explanation stands out as it can explain the three states simultaneously,see e.g.Refs.[198-200].Particularly in Ref.[200],the LHCb data are described quite well by the interaction constructed with heavy quark spin symmetry and actually fourPcstates,instead of three,show up,corresponding toandmolecules.A hint of a narrowPc(4380)was reported in the analysis of Ref.[200].The rest threePcstates related topredicted there have no signals up to now.
In the vector meson saturation model considered here,the two contact terms constructed considering only HQSS[198,200-202],corresponding to the total angular momentum of the light degrees of freedom to be 1/2 and 3/2,are the same,similar to theHinteraction discussed in Section IV.B.1.As a result,7molecular states[195]with similar binding energies are obtained,and the twostates with different total spins,corresponding to thePc(4440)andPc(4457),degenerate.The degeneracy will be lifted by considering the exchange of pion and other mesons and keeping the momentum-dependent terms of the light vector exchange.
It is natural for the isoscalarto form bound states if the abovePcstates are considered as the isospin-1/2molecules since the interactions from the light vector exchange are the same in these two cases,see Table VIII.Note that such states have been predicted by various works[203-212].
Recently,Ref.[83]reported an exotic state name dPcs(4459)in the invariant mass distribution ofJ/ψΛin→J/ψK-Λ.Even though the significance is only 3.1σ,several works[213-217]have explored the possibility ofPcs(4459)being a molecule of,and the finding here supports such an explanation that the structure could be caused by two isoscalarmolecules.
Furthermore,Ref.[218]moved forward to the double strangeness systems and claimed thatandmay form bound states withJP=3/2-and 5/2-,respectively.Theφexchange for such systems yields repulsive interaction at leading order,see Table VIII,and the bound states obtained in Ref.[218]result from other contributions,including the exchange of pseudoscalar and scalar mesons,the subleading momentum dependence from theφexchange and coupledchannel effects.
V.SUMMARY AND DISCUSSION
The whole spectrum of hadronic molecules of a pair of charmed and anticharmed hadrons,considering all theS-wave singly-charmed mesons and baryons as well as thesℓ=3/2P-wave charmed mesons,is systematically obtained usingS-wave constant contact potentials saturated by the exchange of vector mesons.The coupling of charmed heavy hadrons and light mesons are constructed by implementing HQSS,chiral symmetry and SU(3)flavor symmetry.
The spectrum predicted here should be regarded as the leading approximation of the spectrum for heavyantiheavy molecular states,and gives only a general overall feature of the heavy-antiheavy hadronic molecular spectrum.Specific systems may differ from the predictions here due to the limitations of our treatment.We considered neither the effects of coupled channels,nor the spin-dependent interactions,which arises from momentum-dependent terms that are of higher order in the very near-threshold region,nor the contribution from the exchange of pseudoscalar and scalar mesons,nor the mixing with charmonia.Nevertheless,the spectrum shows a different pattern than that considering only the one-pion exchange(see,e.g.,Ref.[196]),which does not allow the molecular states in systems such asDandΣc,where the one-pion exchange is forbidden without coupled channels,to exist.
In total 229 hidden-charm hadronic molecules(bound or virtual)are predicted,many of which deserve attentions:
1.The pole positions of the isoscalarDwith positive and negativeC-parity are consistent with the molecular explanation ofX(3872)and~X(3872),respectively.There is a shallow bound state in the isoscalarDsystem,consistent with the recent lattice QCD result[100].
4.Instead of associating theX(4140)with amolecule like some other works did,our results prefer theto form a virtual state.The peak in the invariant mass distribution ofJ/ψφmeasured by LHCb just at thethreshold is consistent with this scenario,according to the discussion in Ref.[38].
7.Light vector meson exchanges either vanish due to the cancellation betweenρandωor are not allowed in the isovectorsystems andsystems.However,the vector charmonia exchanges may play an important role as pointed out in Ref.[115],and theZc(3900,4020)andZcs(3985)could well be theand—virtual states.
When the light vector meson exchange is allowed,the results reported here are generally consistent with the results from a more complete treatment of the oneboson exchange model(e.g.,by solving the Schr¨odinger equation).For example,the binding energy of the isoscalarD¯D[99]andbound states from theρandωexchanges fit the spectrum well;a similar pattern of molecular states related to theX(3872)was obtained in Ref.[99]and the light vector exchange was found necessary to bindtogether;thebound states corresponding to thePc(4440)andPc(4457)were obtained via one boson exchange in Ref.[219],and the degeneracy of the two states withJ=1/2 and 3/2 is lifted by the pion exchange and higher order contributions from theρandωexchange.We should also notice that there can be systems whose contact terms receive important contributions from the scalar-meson exchanges.
We expect that there should be structures in the near-threshold region for all the heavy-antiheavy hadron pairs that have attractive interactions at threshold.The structure can be either exactly at threshold,if the attraction is not strong enough to form a bound state,or below threshold,if a bound state is formed.Moreover,the structures are not necessarily peaks,and they can be dips in invariant mass distributions,depending on the pertinent production mechanism as discussed in our recent work[38].
When the predicted states have ordinary quantum numbers as those of charmonia,the molecular states must mix with charmonia,and the mixing can have an important impact on the spectrum.Yet,in the energy region higher than 4.8 GeV,where plenty of states are predicted as shown in Figs.1 and 2,normal charmonia should be very broad due to the huge phase space while the molecular states should be relatively narrow due to the large distance between the consistent hadrons.Thus,narrow structures to be discovered in this energy region should be mainly due to the molecular structures,being either bound or virtual states.
Among the 229 structures predicted here,only a minority is in the energy region that has been studied in detail.The largest data sets from the current experiments have the following energy restrictions:direct production of the 1--sector ine+e-collisions goes up to 4.6 GeV at BESIII;the hidden-charmXY Zstates produced through the weak processb→c¯csinB→Kdecays should be below 4.8 GeV;the hidden-charmPcpentaquarks produced inΛb→Kdecays should be below 5.1 GeV.To find more states in the predicted spectrum,we need to have both data in these processes with higher statistics and data at other experiments such as the prompt production at hadron colliders,PANDA,electron-ion collisions ande+e-collisions above 5 GeV at super tau-charm facilities.
The potentials in the bottom sector are the same as those in the charm sector,if using the nonrelativistic field normalization,due to the HQFS,and we expect the same number of molecular states in the analogous systems therein.Because of the much heavier reduced masses of hidden-bottom system,the virtual states in the charm sector will move closer to the thresholds or even become bound states in the bottom sector,and the bound states in the charm sector will be more deeply bound in the bottom sector.There may even be excited states for some deeply bound systems.For these deeply bound systems,the constant contact term approximation considered here will not be sufficient.However,due to the large masses,such states are more difficult to be produced than those in the charm sector.
ACKNOWLEDGMENTS
We would like to thank Chang-Zheng Yuan for useful discussions,and thank Fu-Lai Wang for a communication regarding Ref.[218].This work is supported in part by the Chinese Academy of Sciences(CAS)under Grant No.XDB34030000 and No.QYZDBSSW-SYS013,by the National Natural Science Foundation of China(NSFC)under Grant No.11835015,No.12047503 and No.11961141012,by the NSFC and the Deutsche Forschungsgemeinschaft(DFG,German Research Foundation)through the funds provided to the Sino-German Collaborative Research Center TRR110“Symmetries and the Emergence of Structure in QCD”(NSFC Grant No.12070131001,DFG Project-ID 196253076),and by the CAS Center for Excellence in Particle Physics(CCEPP).
Appendix A:Vertex factors for direct processes
The vertex factors in Eq.(46)for different particles are calculated in the following:
·D

·D*
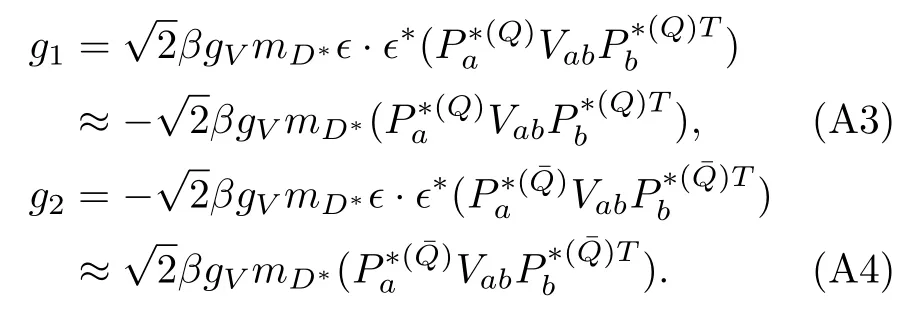
·D1
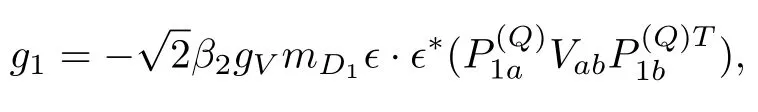
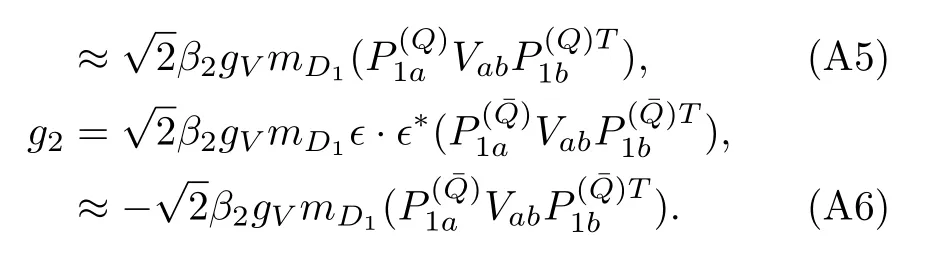
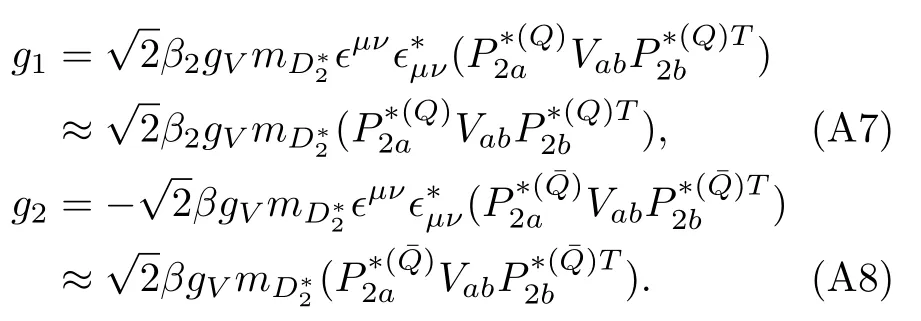
·B¯3
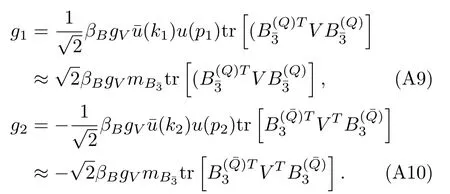
·B6
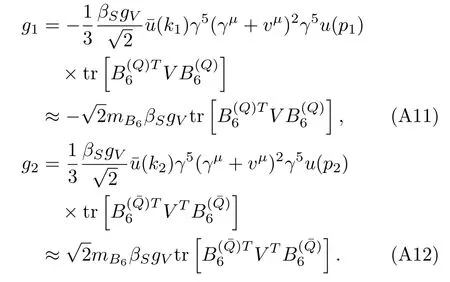
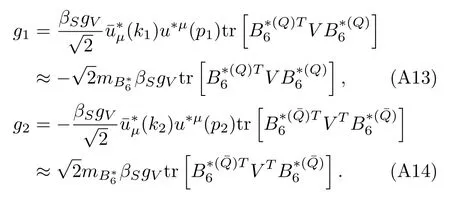
In the above deductions we have usedϵ·ϵ*=−1,=1,=2mand=−2mat threshold.Note that the factors such as,trin the above expressions contain only the SU(3)flavor information and the properties of the corresponding fields have already been extracted.
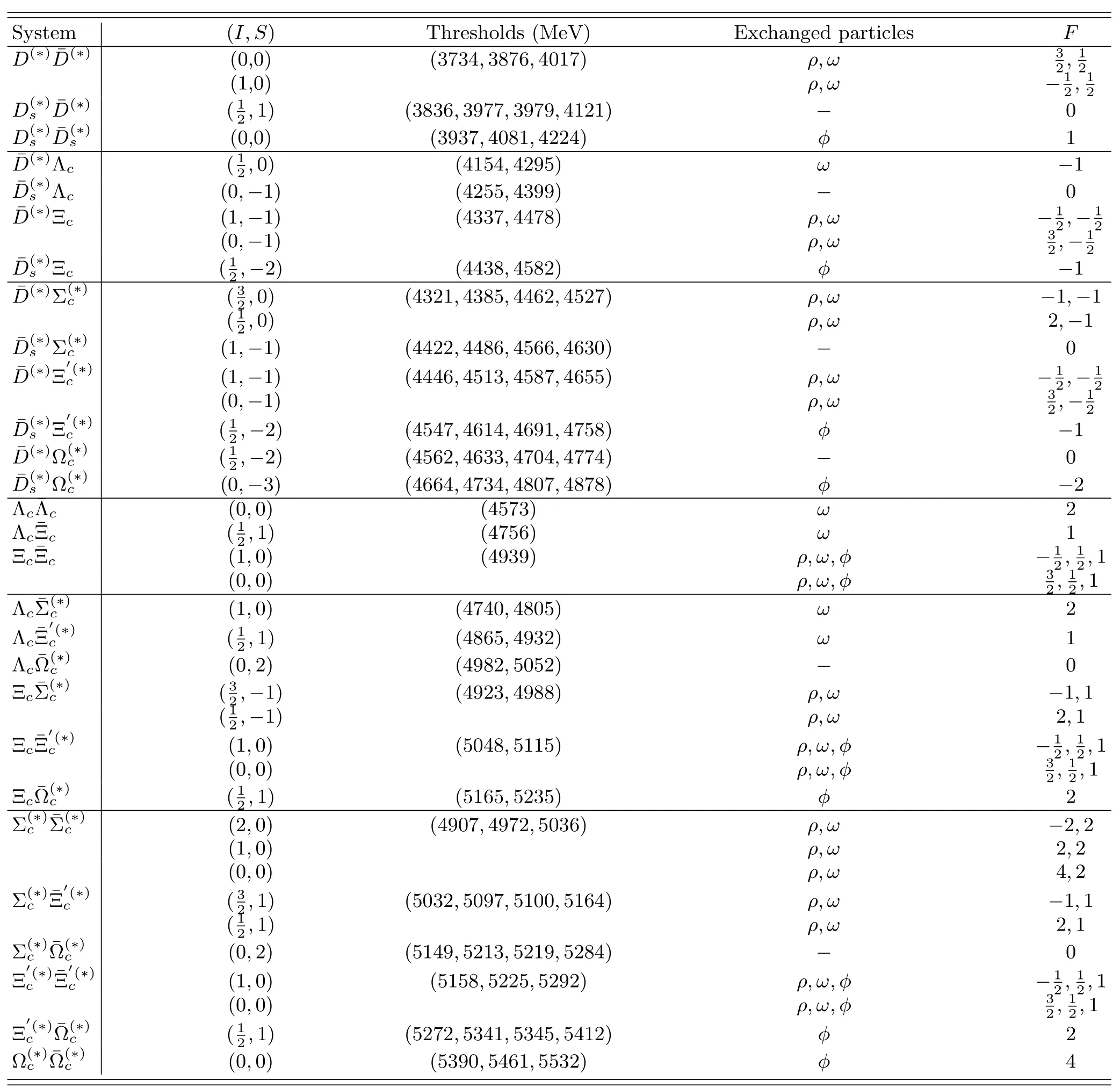
TABLE VIII.The group theory factor F,defined in Eq.(47),for the interaction of charmed-anticharmed hadron pairs with only the light vector-meson exchanges.Here both charmed hadrons are the S-wave ground states.I is the isospin and S is the strangeness.Positive F means attractive.For the systems with F=0,the sub-leading exchanges of vector-charmonia also lead to an attractive potential at threshold.
Appendix B:List of the potential factorF
The details of interactions between all combinations of heavy-antiheavy hadron pairs are listed in Tables VIII and IX.
Appendix C:Amplitude calculation for cross processes
In the following we show the deduction of Eq.(49).
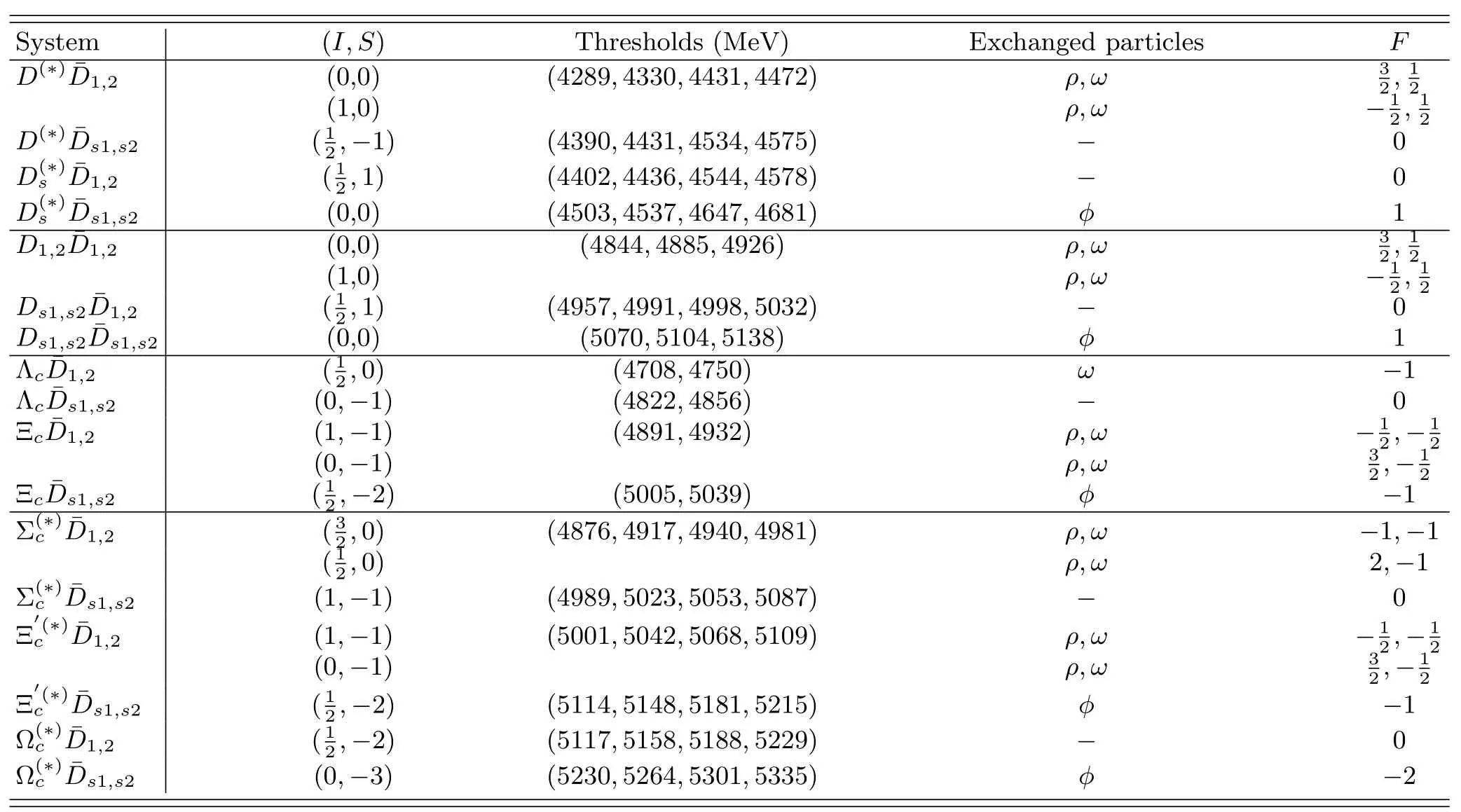
TABLE IX.The group theory factor F,defined in Eq.(47),for the interaction of charmed-anticharmed hadron pairs with only the light vector-meson exchanges.Here one of the charmed hadrons is an sℓ=3/2 charmed meson.See the caption of Table VIII.
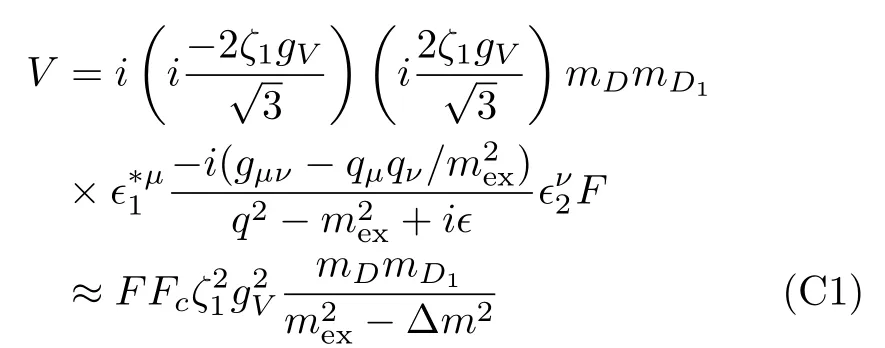
withFc=4/3.
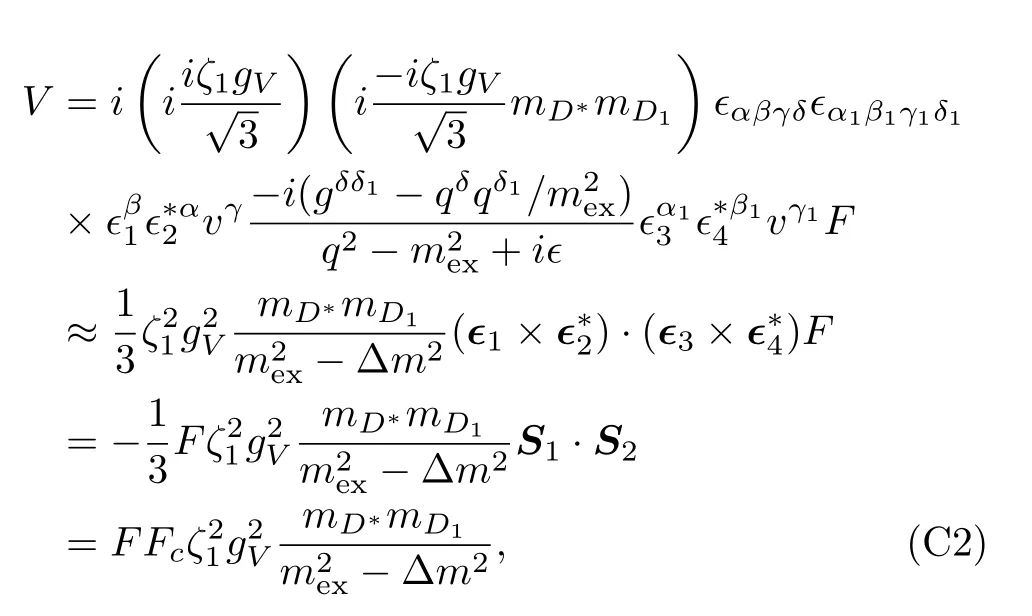
whereSiis the spin-1 operator.Explicitly,S1·
S2=−2,−1 and 1 for total spinJ=0,1 and 2,respectively and in turn we obtainFc=2/3,1/3 and−1/3.
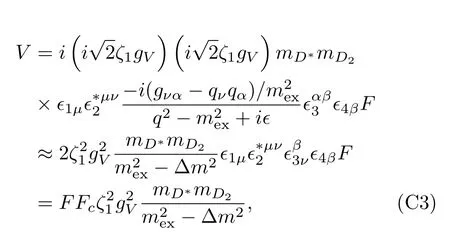
whereFc=−1/3,1 and−2 for total spinJ=1,2 and 3,respectively.
