一种天然气和石油管道屈服强度的检测方法
2021-08-30岑晓燕徐惟诚
岑晓燕,徐惟诚
(宝山钢铁股份有限公司 制造管理部,上海 200941)
钢管静水压爆破试验能较为全面地反映钢管实物的力学性能水平,是管线工程中必不可少的一项检测项目。多个管线钢管产品标准和技术规格书都对静水压试验进行了要求和规定,一般要求静水压爆破试验的实际爆破压力不低于按公称尺寸和母材抗拉强度最小值计算得出的理论爆破压力值。而笔者所在的试验室接到一项试验委托,需用澳大利亚/新西兰标准AS/NZS 2885.5:2012《管道-气态和液态石油 第5部分:现场压力测试》[1]进行试验,并且提供规定非比例延伸率为0.2%时的强度Rp0.2、规定总延伸率为0.5%时的强度Rt0.5、爆破点的半斜率屈服强度(1/2斜率屈服强度)和实际斜率,以及应力-应变曲线和压力-进水量曲线。AS/NZS 2885.5:2012建议经过冷扩径的钢管采用压力-进水量曲线的斜率来确定屈服强度,即以压力-进水量曲线弹性变形期间的斜率的1/2斜率线与压力-进水量曲线的交点所对应的应力作为屈服强度。由于试验室的爆破试验设备是按照SY/T 5992—2012《输送钢管静水压爆破试验方法》[2]设计的,仅限于计算钢管内的压力值,对于测试屈服强度及斜率计算等内容,鉴于现有设备及测试软件的限制,不能自动获得。为此,笔者通过试验探讨了利用现有设备获取实际斜率以及屈服强度的定量求取方法,为试验设备扩展出屈服强度计算能力提供了技术方案。
1 试验方法
试样为X42M钢级的UOE焊管管段,选用两种规格:φ914 mm×12.7 mm(T1、T2号钢管)、φ914 mm×11.9 mm(T3、T4号钢管),其中T1和T3号钢管为光管,T2和T4号钢管为涂层管,试样长度约为5 m。
试样两端采用钢板焊接密封,密封板上还用加强筋焊接固定。试验前先向试样中注满水,排净空气,然后往试样中继续注水加压。借助现有钢管静水压爆破试验设备进行试验。由于静水压爆破试验设备未提供求屈服强度的方法,决定采用Excel软件求取屈服强度。
笔者采用AS/NZS 2885.5:2012的方法计算静水压爆破试验过程中压力-进水量曲线直线段的斜率,即实际斜率,以及各种屈服强度数据。因此,在管段试样不同位置安装两个拉线传感器,以跟踪钢管周长的应变数据,即环向应变数据,当应变量达到1%时拆除传感器,随后继续加压至试样破裂。
2 计算方法
2.1 理论斜率的计算方法
AS/NZS 2885.5:2012规定,加压过程中,需要对压力-进水量曲线的实际斜率和按附录C计算的理论斜率进行比较,差值应小于10%,否则必须停止试验,并分析原因,直到满足该规定。
该次静水压爆破试验属于非约束性试验,即周向和纵向均没有限制变形,因此采用AS/NZS 2885.5:2012附录C给出的公式计算理论斜率,如下:
(1)

当以水作为试验介质时,ΔT=0 ℃,Δp=1 kPa,进水量-压力的斜率Δpfactor可通过下式求取:
(2)
钢管测试部分的初始压力p可通过下式求取:
(3)
式中:pleakmin为泄漏时的试验压力,取设计压力的1.1倍,26 038.7 kPa;Zmax为钢管服役海拔时的最高海拔;Zmin为最低海拔;ρ为水的密度,取1 000 kg·m-3;gc为重力加速率,取9.81 m·s-2。
试验介质的可压缩性A可通过下式求取:
(4)
式中:Ttest是试验过程中的初始温度。
算出A后即可求出Δpfactor。钢管加压体积增加后,压力-所增加体积曲线的斜率pVslope可由下式计算出:
pVslope=ΔpfactorV0
(5)
式中:Vslope为试验过程中压力-进水量呈线性关系时总水量的体积,理论斜率为1/pVslope。
2.2 弹性段实际斜率的计算方法
试样弹性段实际斜率可以通过试验过程的进水量和压力数据计算获得。数据拟合可以采用Excel、Matlab、Origin等软件进行,笔者采用Excel软件进行数据分析及曲线绘制。用Excel图表类型中的散点图绘制成压力-进水量曲线,并采用Excel将弹性段的数据进行拟合,得到直线段的拟合方程,即求得实际斜率,具体案例见图1。图1为光管T1压力-进水量曲线的压力-进水量拟合曲线,光管T1压力-进水量曲线的实际斜率为0.432 6。
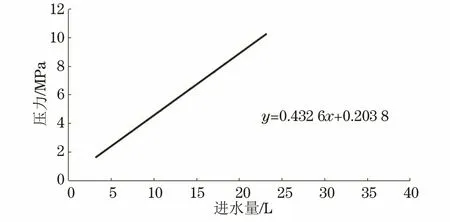
图1 光管T1的压力-进水量拟合曲线Fig.1 Fitting curve of pressure-water inflow of uncoated pipe T1
2.3 屈服强度的测定和计算方法
2.3.1 1/2斜率屈服强度的测定和计算方法
AS/NZS 2885.5:2012中静水压爆破试验的压力-进水量曲线1/2斜率屈服强度的测定,可以使用放大后的压力-进水量曲线进行分析,根据坐标值的变化率来确定。如弹性段直线斜率为0.3 MPa·L-1,当压力-进水量曲线圆弧段切线斜率为0.15 MPa·L-1时,相切点即为屈服强度。而曲线放大倍率与压力和进水量测量的分辨率以及曲线的波动性有一定的关系,倍率过高时,曲线有跳动现象并不便于1/2斜率屈服强度的求取。
1/2斜率屈服强度可以根据压力、进水量通过设备安装的软件求取,也可借助Excel软件求取。采用Excel软件时,先采用巴洛(Barlow)公式将压力转换为环向应力,巴洛公式见式(6)[3],再将导出的进水量和应力数据用Excel软件图表类型中的散点图绘制出应力-进水量曲线。1/2斜率屈服强度的计算即采用压力-进水量曲线,在曲线上求得斜率线以及相应的1/2斜率切线,找出对应的切点即得出屈服强度。
S=pD/2t
(6)
式中:S为钢管内部静水压力在管壁上产生的单位周向应力。
2.3.2Rp0.2和Rt0.5的测定
Rp0.2和Rt0.5从应力、应变数据中求得(应变记录至1%),其应变值由拉线传感器采集。另外也可采用Excel软件,将导出的压力值转换为环向应力值,用散点图绘制成应力-应变曲线,在曲线上画出斜率线以及0.2%对应的平行线、0.5%对应的垂直线,分别找到他们与曲线相应的交点,得出Rp0.2以及Rt0.5的数值,如图2所示。
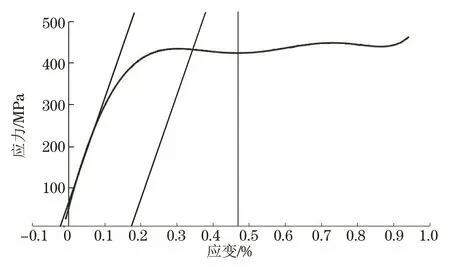
图2 Rp0.2和Rt0.5的求取示意图Fig.2 Schematic diagram of Rp0.2 and Rt0.5 calculation
3 分析与讨论
通过上述方法,可以将4根试样借助钢管静水压爆破试验获得的数据绘制成3类试验曲线,从中计算出实际斜率、1/2斜率屈服强度、Rp0.2及Rt0.5。
最终算得4根试样的理论斜率和实际斜率见表1。AS/NZS 2885.5:2012规定,在加压过程中,压力-进水量曲线的实际斜率和理论斜率差值率应小于10%,否则必须停止试验,并分析原因,直到解决该问题。从表1可知,4根试样的理论斜率和实际斜率差值均小于10%,符合标准要求。

表1 试样的理论斜率和实际斜率Tab.1 Theoretical slopes and actual slopes of the samples
通过数据统计、绘图和计算得出1/2斜率屈服强度、Rp0.2及Rt0.5,见表2。由表2可知,通过前文所述的方法和计算公式可以方便快捷地获得钢管静水压爆破试验的1/2斜率屈服强度、Rp0.2及Rt0.5,其中与钢管管体横向拉伸试验得到的Rt0.5数据基本一致,表明上述方法获得的数据可靠。
4 结论
(1)笔者提出的计算方法得到了1/2斜率屈服强度、实际斜率、Rp0.2及Rt0.5,且Rt0.5与实际拉伸试验得到的数据基本一致。
(2)当试验室没有AS/NZS 2885.5计算屈服强度的钢管静水压爆破试验设备时,可借助Excel软件并套用标准给出的公式,来求取所需要的屈服强度。根据此计算方法,可以为钢管静水压爆破试验设备扩展出屈服强度计算能力。
