约束阻尼结构力学性能研究与参数优化
2021-08-30顾赛克邓琼刘悦
顾赛克,邓琼,刘悦
(西北工业大学航空学院,西安710072)
0 引 言
飞机在飞行过程中气动外形和飞行姿态均会引起气流的分离,湍流、扰流、脉冲压力等非定常气动力与飞机结构发生流固耦合会引起飞机结构的振动,进而产生疲劳裂纹,导致结构破坏,这是飞机失效的主要原因。振动疲劳会导致结构产生比常规疲劳更严重的损伤。因此,飞机薄壁结构的振动抑制可以提高飞机的出勤率、服役时间和安全性。
传统的抑振方法主要分为主动控制和被动控制两种。主动振动控制技术是采用压电材料设计合理的阻尼器,利用材料的逆压电效应抑制振动疲劳。但是考虑飞行器结构设计对质量体积要求严苛,且工作环境有低温、低压等特点,在飞行器结构上安装压电阻尼器难以满足工况要求,且其实施过程复杂,成本偏高,不适于工程应用。被动振动控制技术则是对结构进行阻尼处理的有效方法。较为常见的被动阻尼抑振方法是在目标结构表面粘贴黏弹性阻尼材料,在交变载荷作用下,由于应力应变不同步产生能量耗散,有效降低振动响应。V.Levraea等曾将黏弹性材料粘贴在飞机结构表面,吸收耗散结构的振动能量,从而延长飞机结构的使用寿命。这种粘贴在结构表面吸收和耗散振动能量的结构称为附加阻尼。
早期对约束阻尼结构的研究基本集中在理论方面。Kerwin等将阻尼层置于一个无限长的简支夹层梁中制成三层结构,以复数形式表示夹心梁的弯曲刚度,研究了阻尼层在该三层梁结构中所形成的减振效应,奠定了约束阻尼结构复刚度法 的 理 论 基 础 ;R.A.Ditaranto在 此 基 础 上 提 出了有限长度下含黏弹性层夹心梁受到弯曲变形所产生的振动分析理论,同时得到了任意便捷条件下夹心梁的轴向位移六阶偏微分方程;熊志远等利用强迫共振法测试四种阻尼结构试样,分析试样频谱图共振曲线,并从微观力学角度对自由阻尼结构、约束阻尼结构、多层阻尼结构的减振机理进行了分析;G.Parthasarathy等研究了应用于矩形板结构的无约束部分的阻尼处理,通过有限元方法分析了不同阻尼层配置的有效性,考察了阻尼处理对结构的模态频率、阻尼损耗因子和模态振型的影响,同时进行了实验研究;A.Lumsdaine等建立了不同的有限元模型,研究了自由阻尼结构和约束阻尼结构的梁和板的阻尼层优化设计;J.L.Marcelin等开发了部分覆盖约束阻尼结构的有限元模型,并使用非线性优化方法优化约束阻尼贴片的尺寸和位置,以最大化阻尼因子;Ma Xin‐bo等基于等效材料特性,提出了一种将多层约束阻尼结构简化为单层结构的方法并进行了有限元建模验证。
大量的研究工作致力于获得基础结构上约束阻尼层的优化设计。房占鹏等针对平稳随机激励下约束阻尼结构进行了布局优化,采用虚拟激励法对平稳随机激励下约束阻尼结构振动响应进行分析和优化;Cai C等用遗传算法研究了简支梁和圆柱形壳体上部分覆盖的约束阻尼材料的剪切模量和位置以及长度等参数,以达到振动能量最小的目的;P.P.Hujare等对用不同黏弹性阻尼层组成的约束阻尼结构处理的梁结构进行了实验研 究;M.R.Maheri在正方 形板上研 究了不同约束阻尼对模态阻尼的影响;袁月生等通过两边简支约束条件下的单点锤击实验和ANSYS模拟研究了阻尼层厚度、阻尼层切口对局部约束阻尼结构振动的影响;曾昭阳等基于模态应变能法对厚圆柱壳结构中约束阻尼层材料的损耗因子、刚度及阻尼层的厚度进行了参数分析,分析了阻尼层参数对整体结构模态阻尼比的影响规律;艾振等基于经典的自由阻尼和约束阻尼耗能原理,提出了一种含弹性约束的具有剪切和弯曲复合耗能机制的复合阻尼层结构;王晓建等基于有限元法建立数值仿真模型,研究了约束阻尼复合结构的隔声性能,分析了黏弹性夹层对约束阻尼复合结构隔声性能的影响机理;郭君等针对阻尼材料性能测试的几种实验方案的准确和合理性进行有限元仿真研究,确定和改进了最优实验方案;L.Rouleau等提出了一种有效模拟薄约束黏弹性层的仿真方法;F.Kpeky等研究了各种参数对多层黏弹性结构阻尼性能的影响。以上研究从不同角度促进了约束阻尼结构的发展,但是由于约束阻尼结构针对不同基体结构的复杂性,针对不同结构与材质的基体结构,仍需要比较有针对性且完备的研究。
本文以飞机典型薄壁结构之一的悬臂梁结构作为基体结构,研究约束阻尼材料各层材料的力学性能以及设计参数对结构整体阻尼效率的关系,以优化后的结构参数作为指导制备约束阻尼结构,通过仿真和实验的手段验证约束阻尼结构对受振动加载的结构有高效的降低共振应力应变幅值的作用,并对不同抑振目的的总体结构设计提出指导性意见。
1 约束阻尼结构材料选择及性能测试
阻尼层通常选用聚合物材料,此类材料具有黏弹性或超黏弹性特征,应力与应变之前存在相位差,上下层相连接的结构变形差产生的剪切变形使阻尼材料在循环加载过程中产生应变滞后,从而将振动能量转变成热能散发出去,如图1所示。其中被封闭曲线包围的面积表示材料在承受交变载荷过程中损耗的能量。

图1 弹性材料与黏弹性材料承受交变载荷下的应力-应变曲线Fig.1 Stress-strain curves of elastic material and viscoelas‐tic material under alternating load
本文选择3M公司生产的ISD112型阻尼材料作为阻尼层材料,该材料的使用温度在10~38℃范围内,并能保持较高的阻尼损耗因子,自然老化稳定性好。而且该阻尼材料为单层0.125 mm的两面均具有黏性的双面胶,能够在不使用其他胶黏剂的条件下与约束层及基体材料粘结固化成型,且方便叠层使用,从而对阻尼层厚度进行优化和设计,易于工程应用。
3M-ISD112是一种聚丙烯酸酯聚合物,由丙烯酸正丁酯和少量硫化活性单体共聚而成,其主要成分化学式如图2所示。

图2 ISD112型阻尼材料主要成分Fig.2 Main component of ISD112 damping material
聚丙烯酸脂本身由于羟基侧链增大了分子间力与旋转空间位阻,致使分子链僵硬,且分子结构规整,易于结晶,因此,常温下缺乏橡胶性能。只有当羟基经酯化后,烷基会屏蔽极性基团,降低分子间力,增大了分子链的柔性。随着烷基侧链的增长,这种屏蔽内塑作用增加,增至聚丙烯酸正丁酯时成为橡胶状弹性体。因此其作为阻尼材料具有良好的阻尼特性和较宽的使用温度,又具有较好的黏弹性。
约束层材料选择方面,由于约束阻尼结构许用载荷、静强度和疲劳抗性均由约束层提供,因此约束层材料的选择就变得尤为重要。参考胶接修补的设计要点,一个有效的补片设计应当具有提供可观的许用载荷、静强度以及疲劳抗性。本文选择玻璃纤维/环氧复合材料作为约束层材料。玻璃纤维具有较高的比强度,而且属于轻质材料,满足质量要求。该材料是由威海光威复合材料有限公司生产的G12500型号玻璃纤维预浸料成型的厚度为0.2 mm的玻璃纤维板。预浸料的材料特性如表1所示。

表1 G12500型号的玻璃纤维预浸料典型材料特性Table 1 T ypical material characters of glass fiber prepreg of G12500
该玻璃纤维板的性能如表2所示,E
为玻璃纤维纵向拉伸模量;E
为其横向拉伸模量;μ
为泊松比 ;G
,G
,G
分 别 为 三 个 平 面 内 的 剪 切 模 量 。可以看出:此种玻璃纤维板沿纤维方向弹性模量较大,具有较高的刚度,发生纵向变形时横向变形量较小,板材的形状稳定性好。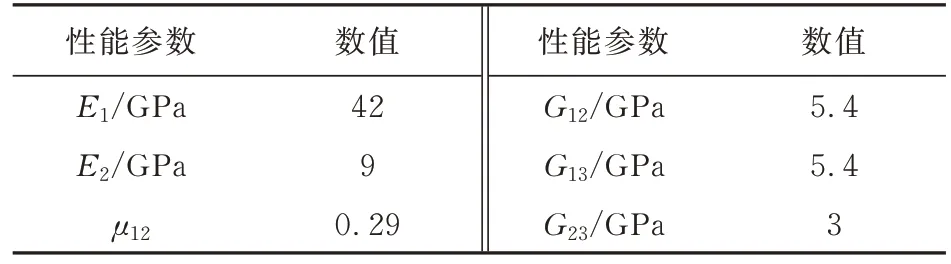
表2 玻璃纤维单层板性能Table 2 Properties of glass fiber monolayer board
在室温下对ISD112阻尼胶以及玻璃纤维单层板进行DMA分析,对两种材料的阻尼损耗因子进行测定,剪切模式下结果如图3所示。
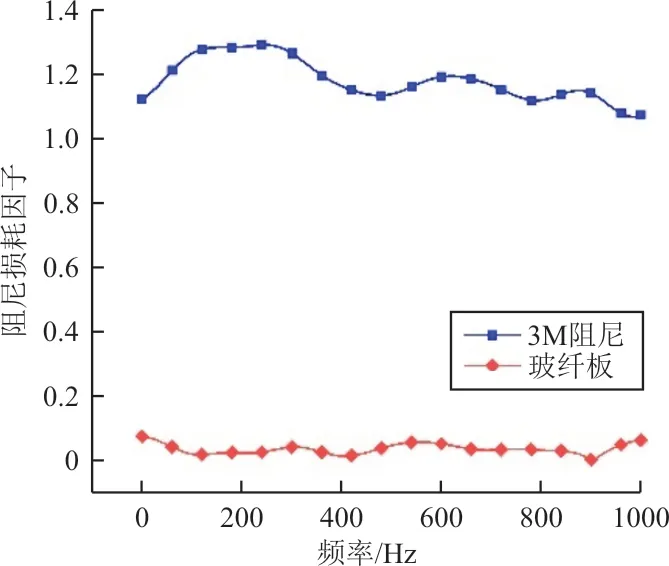
图3 约束阻尼结构各层材料的阻尼损耗因子Fig.3 Loss factor of each layer material of constrained damping structure
从图3可以看出:该黏弹性材料能在1~1 000 Hz范围内保持阻尼损耗因子均大于1,而玻璃纤维复合板的阻尼损耗因子相比很小,只有不到0.1。
2 约束阻尼结构抑振性能研究
2.1 约束阻尼结构的制备
玻璃纤维单向板和3M-ISD112阻尼材料如图4所示,ISD112阻尼材料粘附于光面纸上,在制作约束阻尼片时需要将阻尼胶逐层铺设到玻璃纤维单层板上,再将光面纸去除。约束阻尼结构试样如图5所示。

图4 玻璃纤维单层板和ISD112阻尼胶Fig.4 Fiberglass monolayer and ISD112 damping adhesive

图5 约束阻尼结构试样Fig.5 Constrained damping structural sample
本文制备两种形式的约束阻尼片用于薄壁结构抑振,分别为两层结构和三层夹心结构,示意图如图6所示。

图6 约束阻尼片结构示意图Fig.6 Schematic diagram of constrained damping structure
双层约束阻尼片结构(图6(a))为常规约束阻尼结构,其主要作用是在基体受周期性振动载荷产生弯曲或扭曲变形时,利用约束层和基层材料的变形差使阻尼材料产生剪切和拉伸变形,从而利用阻尼层的黏弹性和长链分子结构产生应变滞后和能量消耗达到抑制振动的效果。
三层夹心约束阻尼片(图6(b))在双层结构抑振效果的基础上,与基层结构直接胶粘的约束层材料本身有抵抗变形的能力,可以提高机体材料本身的刚度和强度,从而降低结构载荷,也能起到抑制振动的效果。
用METTLER公司生产的861e型动态热机械分析仪(DMA)对制备好的约束阻尼补片进行实验。由于约束阻尼补片在结构振动时,主要发生弯曲变形,因此DMA测试采用的模式为三点弯曲模式,分别测试双层和三层结构约束阻尼片的模量与阻尼损耗因子。
2.2 三点弯曲测试
DMA分析仪能够测试不同温度或频率下材料的动态力学性能,本文主要考察约束阻尼的阻尼损耗因子对频率的依赖性。仪器通过设置力和位移两个幅值来调整振动测试时的加载上限,对于该实验,力幅值设置为5 N,位移幅值设置为10μm,测试频率范围为1~300 Hz。实验测量得到阻尼损耗因子η
,储能模量E′
、耗能模量E″
。约束阻尼片在三点弯曲模式下的阻尼损耗因子和储能模量与频率的关系如图7所示。

图7 三点弯曲模式测得的损耗因子和储能模量结果Fig.7 Loss factor and energy storage modulus measured in three-point bending mode
从图7可以看出:约束阻尼结构的损耗因子较玻璃纤维板有较大提升,其中双层结构的损耗因子提升到0.2~0.6左右,三层结构约束阻尼更是稳定在0.6左右,同时三层结构的储能模量要比双层结构的储能模量高20%左右,其与基体结构直接粘贴的下层玻璃纤维板层能在结构经历振动激励产生变形时提供一定的补强作用。因此从结构性能上看,三层结构的约束阻尼片性能要优于双层结构。但是三层结构约束阻尼片比双层结构厚,附加质量也更大,在基体结构对结构厚度和质量要求比较严格的情况下适用范围要比双层结构更局限。因此在选择具体的基体结构所用的约束阻尼结构时,要权衡利弊,也要对约束阻尼结构进行一定的参数设计,从而更好地满足工程需求。
3 约束阻尼补片的参数设计
对于飞行器结构,典型的悬臂梁式结构主要包括腹鳍、垂尾、扰流板等。这类结构在飞行器运行过程中经常受到非定常气动载荷影响,从而产生振动疲劳损伤。约束阻尼修补能极大地降低薄壁结构的共振响应,是一种提高结构寿命的有效有段。但是由于飞机结构对结构厚度和质量的严格要求,约束阻尼结构需要进行参数设计,以更轻薄的形式实现更高效的抑振效果。本文采用有限元仿真软件,对不同厚度下的悬臂梁/薄板类飞机典型结构的修补进行建模计算,对影响约束阻尼片阻尼效率的主要参数进行设计研究。
采用ABAQUS有限元仿真软件对阻尼效果较好的三层约束阻尼片参数进行设计。悬臂梁结构的尺寸如图8所示,厚度为2 mm。

图8 悬臂梁模型尺寸Fig.8 Model dimensions of cantilever beam
在使用有限元软件建模时,铝悬臂梁与阻尼层采用三维实体单元,复合材料约束层采用壳单元。分析步模式先选择频率分析步对结构进行模态分析,再使用模态稳态动力学模拟正弦扫频,以计算模型的频率响应曲线。
其中,约束阻尼片中的约束层建模时截面选取为复合材料多层板,并定义每一层的方向;黏弹性材料参数如表3所示。玻璃纤维复合材料板的模量参数如表2所示。为了简化模型,忽略黏弹性材料的频变特性与温变特性,取室温下的平均值作为阻尼材料的损耗因子。因此取阻尼材料的损耗因子为1,约束层的损耗因子为0.1。胶层则采用tie连接进行模拟,不考虑老化脱粘等情况。

表3 约束阻尼补片胶接修补模型材料参数Table 3 Material parameters of the constrained damping structures
为了直观地表示模态响应的应力峰值大小,在载荷步骤中加入重力并设置扫频激励加速度为1g
,扫频范围为1~300 Hz。在划分网格时,实体单元采用C3D8R八节点六面体单元,壳单元采用S4R四节点平面单元。建立的悬臂梁约束阻尼模型如图9所示,对于悬臂梁结构,一阶模态应力响应峰值最大,对于约束阻尼结构的抑振效果最具研究意义,故仿真计算时主要以结构的一阶模态响应作为参考对约束阻尼结构进行优选和设计。
图9 约束阻尼补片胶接修补悬臂梁结构有限元模型Fig.9 Finite element model of cantilever beam structure repaired with adhesive damping patches
经过计算,在对悬臂梁结构进行约束阻尼处理后,其一阶固有频率稍微增大,结构的一阶模态振型并没有改变,如表4所示。

表4 附加阻尼前后悬臂梁模态频率对比Table 4 Modal frequency comparison of cantilever beam structure before and after additional damping structure
修补前后的Mises应力云图如图10所示,可以看出:由于约束阻尼片粘贴在应力危险区,使得一部分原结构的应力传递至约束阻尼片上,结构原有应力危险区面积有所减小,最大应力值也降低了很多。这说明约束阻尼片能够在保持结构原有模态频率与振型的前提下,有效降低结构危险区域的振动应力幅值,并将结构的高应力区域转移至其他区域分摊应力水平。

图10 粘贴约束阻尼前后结构一阶固有频率Mises应力云图Fig.10 First order natural frequency Mises stress nephogram of structures with and without constrained damping structure
3.1 阻尼层厚度设计
为了研究约束阻尼片各层厚度对铝悬臂梁结构抑振效果的影响,建立多个阻尼层厚度的补片模型。根据补片设计要求,补片的厚度不应超过修补结构的50%,据此设置五种补片阻尼层与悬臂梁结构厚度的比例,分别为1∶2、1∶4、1∶5、1∶8和1∶10,建立不同的约束阻尼片模型,上下约束层层数固定为单层,厚度为0.2 mm。计算在原悬臂梁一阶模态频率处每一个模型的结构阻尼损耗因子,如图11所示。
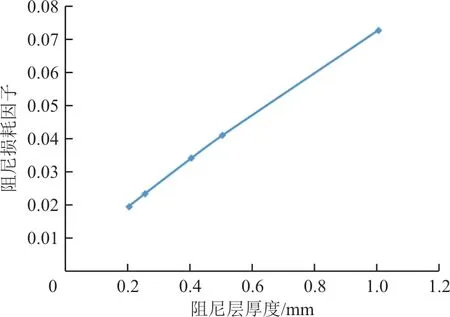
图11 结构损耗因子随阻尼层厚度变化趋势Fig.11 The structural loss factor changes with the thickness of damping layer
从图11可以看出:结构的阻尼损耗因子是随着阻尼层厚度的增加而增加的,而且几乎可以认为两者是正比关系。分析认为,结构整体的阻尼损耗因子主要是由阻尼层黏弹性材料决定的,相对于黏弹性材料,金属材料和玻璃纤维复合材料的损耗因子较小,因此不断增加阻尼层的厚度,也就是不断增大黏弹性材料在结构中所占的比例,结构的阻尼损耗因子自然会随之增大。况且单纯地增大损耗因子并不能体现出结构抗振性能的提升,仅从损耗因子的角度难以确定补片阻尼层的最佳厚度。
因此,在模型输出中选取悬臂梁根部应力危险区某一点与端部某一点为研究对象,计算每个模型同一个应力危险点的应力频响曲线与端部的位移频响曲线。1~100 Hz内应力频响曲线如图12所示,由于该频率段包含结构一阶固有频率,因此有一个明显的峰值。
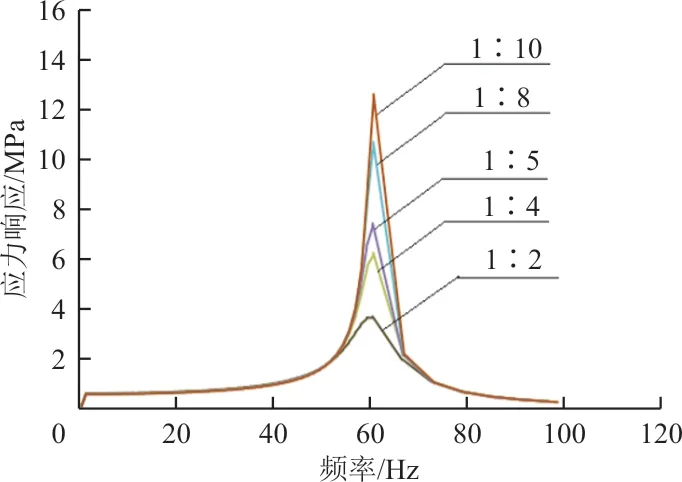
图12 不同阻尼层厚度下悬臂梁结构1~100 Hz段应力频响曲线Fig.12 Stress-frequency curve of cantilever beam struc‐ture at 1~100 Hz with different damping layer thickness
从图12可以看出:随着阻尼层厚度的增加,结构的一阶模态频率略有增加,且所选取的危险点共振应力峰值有显著下降,这是由于阻尼层增加厚度提高结构整体的阻尼损耗因子所致。约束阻尼片在振动过程中发生弯曲变形,上下两层约束层由于变形程度不同,使得中间阻尼层产生剪切变形从而耗散振动能量。因此补片的阻尼层越厚,耗散的振动能量就越多,应力峰值也就下降越多,抑振效果就越好。
但是阻尼层的厚度不能无限制地增加,由于原结构厚度固定,阻尼层厚度在增大到一定程度时,抑振效果的提升就会愈发不明显,与此同时,过高的厚度不仅会引入较大的附加质量,还会使结构处于非平衡的弯曲状态。存在一个阻尼层厚度的平衡点,即能够保证抑振效果,又可以不使结构增重过多或偏离平衡位置。由于振动疲劳破坏主要发生在共振峰附近,因此提取上图共振峰附近的应力峰值与位移峰值,得到了不同阻尼层厚度下共振峰值的曲线,如图13所示。

图13 结构响应峰值随阻尼层厚度的变化趋势Fig.13 Variation trend of structural response peak with change of the thickness of damping layer
从图13可以看出:应力和位移曲线走势基本相同,悬臂梁结构的危险区应力和位移是随着阻尼层厚度的增加而下降的,但是下降的速度却是逐渐变慢的。阻尼层厚度由0.3增加到0.4 mm的过程中,危险区应力峰值由近12降到约8 MPa,而当阻尼层厚度由0.5增加到1 mm时,应力峰值仅由约7降低到了约4 MPa,每增加0.1 mm阻尼层厚度所降低的应力峰值由约4降低到约0.6 MPa。即增加阻尼层厚度在超过0.5 mm后,阻尼“效率”显著降低。在厚度比例超过1∶4后,继续增加阻尼层厚度,对减小共振时的应力与位移幅值效果不大,因此可以认为,对于2 mm的悬臂梁结构,当考虑结构增重以及阻尼层“效率”时,阻尼层厚度在1∶4时补片抑振的效果最好。
之后,本文建立4和5 mm厚度的悬臂梁模型,分析步等参数与2 mm的模型一致,同样经过计算得到1~300 Hz内同一个应力危险点与端部点的应力频响曲线和位移频响曲线,其峰值随阻尼层厚度变化如图14所示。

图14 悬臂梁结构响应峰值随阻尼层厚度的变化趋势Fig.14 The variation trend of cantilever structural response peak with the change of the thickness of damping layer
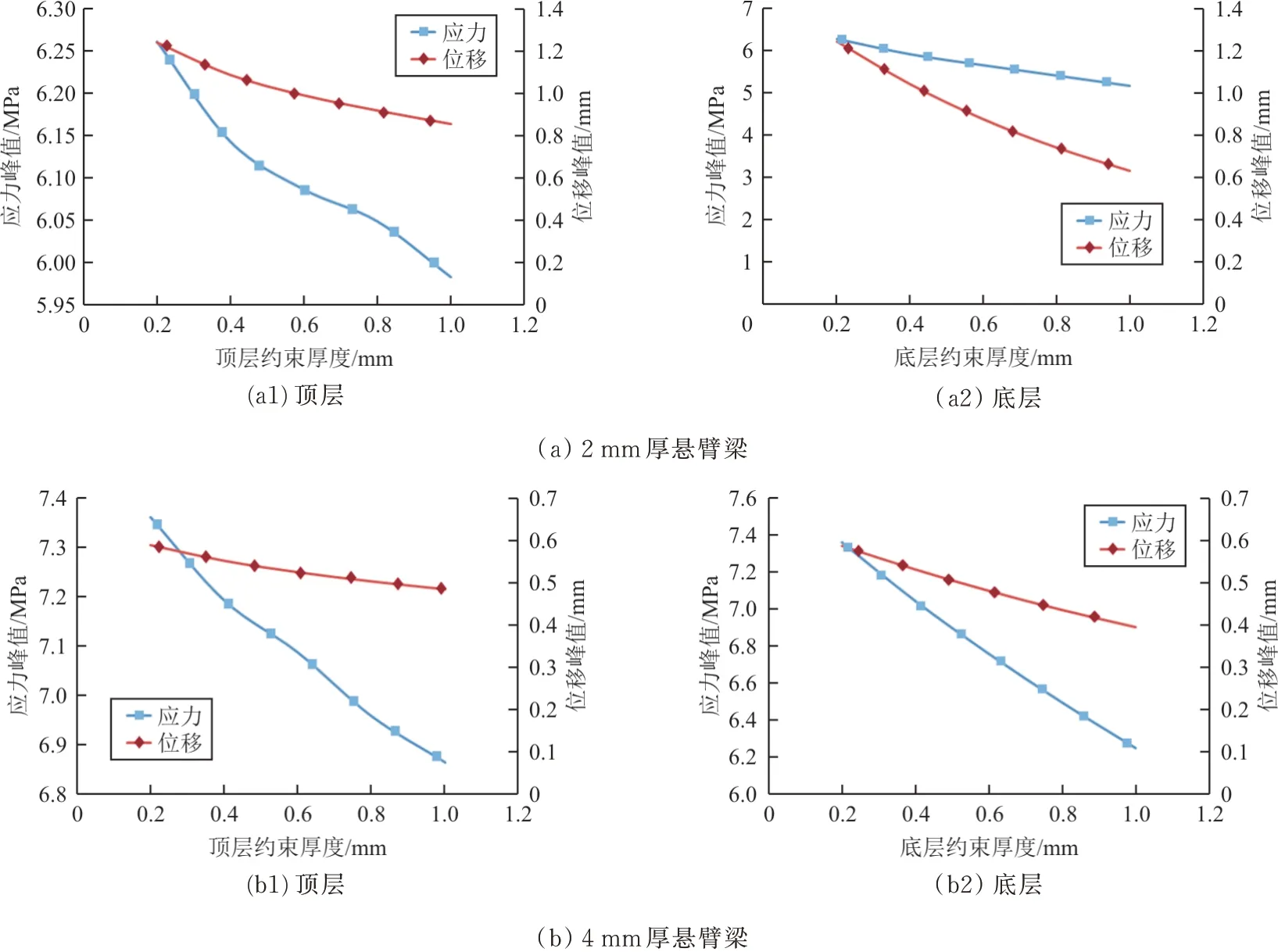
从图14可以看出:随着阻尼层厚度的增加,危险点的应力响应与端部的位移响应变化趋势与2 mm模型结果相似,在阻尼层较薄时,增加厚度可以较快降低应力与位移响应,而随着厚度增加到一定值后,继续增加阻尼层厚度,响应下降的速率会逐渐降低。从图中曲线走势分析可知,1∶4的厚度比例也是4和5 mm铝悬臂梁模型较为合适的补片阻尼层厚度。
3.2 约束层厚度设计
在补片发生弯曲振动时,上下两层复合材料约束层由于变形量不同,使得中间阻尼层产生剪切变形而耗散能量,同时底层约束层还起着抵抗结构变形的作用。过小的厚度会降低补片的强度和刚度,过大的厚度则会降低结构的等效阻尼比和阻尼效率,因此约束阻尼补片的约束层厚度设计也是十分重要的。与阻尼层厚度设计相同,建立2、4和5 mm三种悬臂梁结构预修补模型,其中阻尼层厚度固定为1∶4厚度比例,而复合材料约束层厚度则以层数决定,单层厚度为0.2 mm,故模型厚度以0.2 mm递增。计算三个模型不同上下约束层层数的危险区应力频响曲线与端部位移频响曲线,提取其一阶模态峰值随厚度的变化趋势,如图15所示。
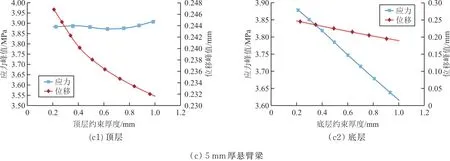
图15 不同厚度悬臂梁模型的响应峰值随补片上下约束层厚度变化趋势Fig.15 The response peak of the cantilever with different thickness varies with the thickness of the upper and lower constraint layer
从图15可以看出:不论是顶层约束层还是底层约束层,其层数的增加对于悬臂梁结构的一阶模态响应的应力峰值与位移峰值效果相比阻尼层较低,甚至由于增加层数提高了约束阻尼补片的质量,导致部分模型应力峰值反而增加了(5 mm厚悬臂梁顶层约束层模型)。分析认为,约束层的复合材料的阻尼损耗因子较低,增加约束层的用量对降低结构的共振响应帮助不大。因此,若仅考虑降低结构模态振动响应,约束阻尼补片的上下两层复合材料均以单层厚度为佳。
3.3 约束阻尼结构尺寸设计
在工程应用中,补片不仅要考虑厚度,还需要考虑其尺寸对修补效果的影响。对于悬臂梁结构,已有研究表明,根部的补片修补效果要好于端部。本文在前人研究的基础上,通过有限元仿真计算约束阻尼补片修补悬臂梁结构的最佳尺寸,分析补片长度对抑振效果的影响。
根据前人研究得到的厚度参数,建立三种典型厚度的悬臂梁模型,分别为2、4和5 mm,每一种模型的约束阻尼补片的厚度均固定:阻尼层厚度与悬臂梁厚度比例为1∶4,约束层厚度为0.2 mm;补片的长度有所不同,根据悬臂梁总长度选取了1∶5、2∶5、3∶5、4∶5和1∶1共5种长度比,建立的不同的模型,每一个模型均从悬臂梁根部进行胶接修补,减少自由端的长度,即附加阻尼结构的长度从悬臂梁夹持端根部开始计算。同样采用1g
加速度激励模拟正弦扫频,输出悬臂梁同一位置处的一阶模态应力峰值与位移峰值,如图16所示。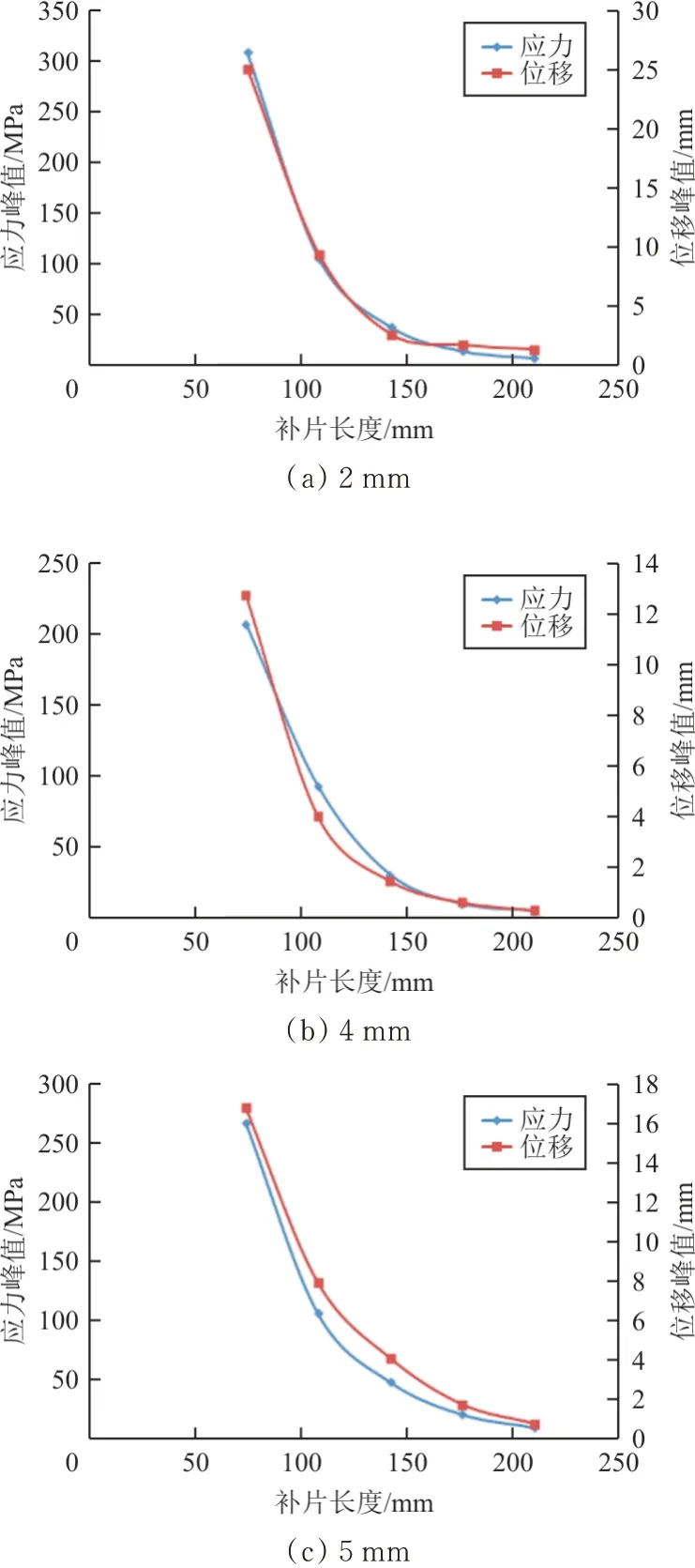
图16 不同厚度悬臂梁响应峰值随补片长度的变化趋势Fig.16 The response peak of cantilever beam with different thickness varies with patch length
从图16可以看出:全铺设约束阻尼时,附加的阻尼材料最多,结构的应力峰值和位移峰值最小,因此抑振效果最好;稍微降低一些约束阻尼片的长度对结构的应力与位移响应影响不大,但是当约束阻尼片长度减少到悬臂梁长度的三分之二以后,结构的振动响应开始急剧增大。分析认为,响应急剧增加一方面是由于黏弹性材料的减少,导致结构损耗因子降低,结构抗振性能下降;另一方面是由于约束层长度的减小,由于约束层不再覆盖悬臂梁结构的端部,导致约束阻尼片在振动过程中的弯曲变形量下降,其耗散的能量降低,故其振动幅值有较大地增加。
三种不同厚度的悬臂梁有限元模型得到了相似的结果,可以认为针对该类型的铝合金悬臂梁结构的振动疲劳问题,采用约束阻尼片进行抑振处理时,增大阻尼层的厚度能够有效提高抑振效果,但阻尼层的厚度与悬臂梁厚度为1∶4时阻尼效率较高;改变约束层厚度对抑振效果影响较小,上下两层约束层以单层厚度为佳;补片的长度与悬臂梁的长度比例至少为2∶3时,约束阻尼结构才能获得较好的抑制振动效果。
4 实验研究
参照仿真计算结果,设计悬臂梁振动测试实验,测量结构在共振时的应力响应峰值,考察双层约束阻尼片和三层约束阻尼片的抑振效果。
4.1 实验件设计
振动测试实验件的设计需要满足以下要求:实验件固有频率不应过高或过低,最好在振动台加载频率范围内;能够确定应力最大值的位置,以便在该位置粘贴应变片;实验件在振动过程中能保持应力危险区的应力分布较为均匀,在设计时避免出现应力集中的位置。
悬臂梁结构实验件与薄板实验件尺寸如图8所示,为了防止实验过程中悬臂梁端部碰到振动台面,取悬臂梁实验件厚度为4 mm。
依据对应的有限元仿真结果,制备了悬臂梁结构的双层和三层约束阻尼片,两种阻尼结构中阻尼层的厚度相同。
4.2 约束阻尼片胶接工艺过程
通过仿真结果可知,在振动载荷作用下,悬臂梁结构的应力危险区在其夹持端根部,而三层结构的约束阻尼片对结构有补强作用,为了让三层结构的约束阻尼结构更好的发挥作用,本文选择在这些区域覆盖约束阻尼片。
4.3 结构振动测试系统
结构振动疲劳与常规疲劳不同,飞行中引发飞机结构产生的振动疲劳破坏的扰动气流主频率大致分布在40~300 Hz,属于高周疲劳范畴,不能使用常规疲劳加载设备。因此,本文选用电动振动台作为激振设备,同时使用数字式振动控制仪实现对结构的振动疲劳加载(如图17所示)。

图17 电动振动台Fig.17 Electrodynamics vibration generator
4.4 实验过程
采用振动台扫频激励的方法,对悬臂梁实验件进行正弦扫频测试。设计一个能够同时夹持多个悬臂梁实验件的夹具,如图18所示。该夹具能在单次实验中夹持多个实验件,以保证实验件处于同一振动条件下。该夹具材料选用45号钢,总质量超过20 kg。经过有限元模态分析,夹具的一阶固有频率为6 000 Hz,远大于实验加载频率,因此可以确保夹具在实验过程中不会发生共振。

图18 悬臂梁实验件夹具Fig.18 Clamp for cantilever beam experiment
为了采集试样的应变响应,实验使用应变片进行数据收集。由仿真结果可知,对于悬臂梁结构只需采集悬臂梁根部弧段处沿着梁方向的应变即可得到结构危险点应变。实验采用基础激励的方式对试样进行正弦扫频加载,加速度激励幅值大小为3g
,扫频的范围是100~1 000 Hz,悬臂梁一阶固有频率在此范围内。实验时通过动态应变仪拾取应变信号,对试样的响应信息进行实时采集,并反馈给振动控制仪,控制仪通过对比反馈信号不断调整输出信号,实现对振动测试系统的闭环控制。4.5 实验结果分析
悬臂梁实验件编号分别为1#、2#和3#,1#是无任何附加阻尼的铝悬臂梁;2#是用三层约束阻尼片进行胶接的铝悬臂梁;3#是采用双层约束阻尼结构进行抑振处理的铝悬臂梁。三个实验件的具体参数如表5~表7所示。

表5 1#悬臂梁实验件参数Table 5 1#experimental parameters of cantilever beam
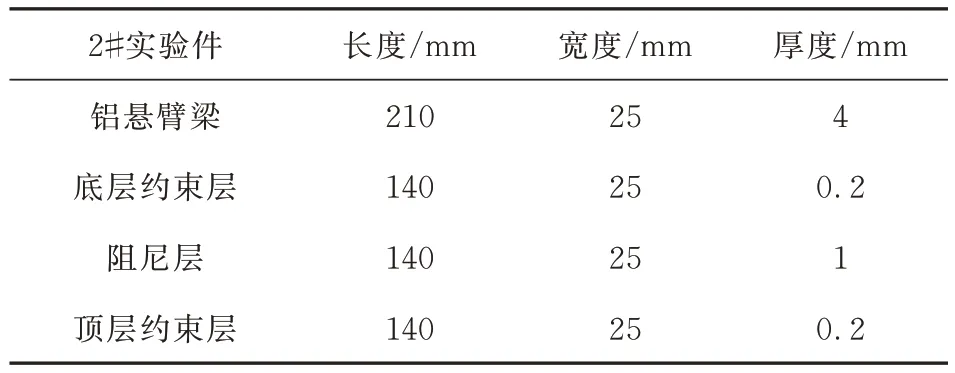
表6 2#悬臂梁实验件参数Table 6 2#experimental parameters of cantilever beam
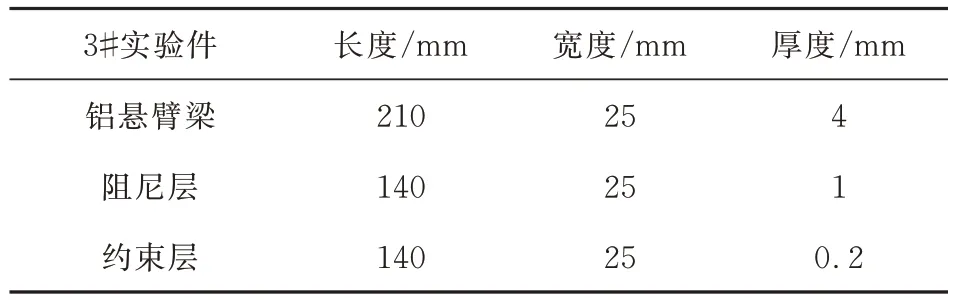
表7 3#悬臂梁实验件参数Table 7 3#experimental parameters of cantilever beam
实验完成后,对采集到的原始振幅时域数据进行傅立叶变换处理,得到试样在频域上的应变响应曲线,变换后的结果如图19所示。
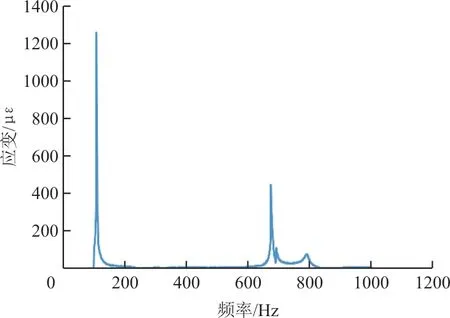
图19 1#悬臂梁实验件的应变频响曲线Fig.19 1#strain-frequency curve of cantilever beam experiment
从图19可以看出:结构的振幅在远离固有频率的频率段时较小,在达到固有频率附近时发生共振,振幅逐渐达到最大值,在固有频率处的共振峰值远大于非共振区域。
将三个实验件的频响曲线结果进行对比,如图20所示。
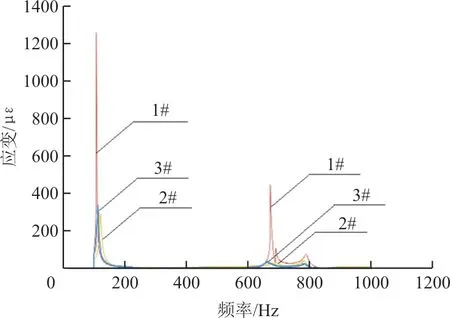
图20 三个实验件的应变频响曲线对比Fig.20 Comparison of strain-frequency curves of three experimental specimens
从图20可以看出:约束阻尼处理后的2#和3#实验件的模态频率稍有改变,各阶应变响应要远小于1#实验件,说明约束阻尼对结构处理后能极大地减少结构共振时的振动响应,结构在不作阻尼处理时的响应大约是附加约束阻尼后的4倍。
计算试样一阶固有频率处的应力峰值,如表8所示,可以看出:附加阻尼之后的实验件2#、3#与原始悬臂梁实验件1#相比,应力响应峰值分别下降了76.75%和72.86%;使用三层片胶接修补的2#实验件的应力峰值最小,为21.09 MPa;2#实验件与采用双层片抑振处理的3#实验件相比,应力峰值减少了14.34%。
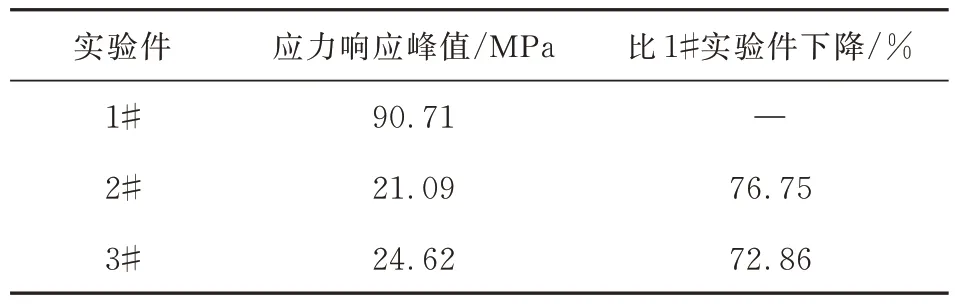
表8 悬臂梁实验件应力响应峰值计算结果Table 8 Calculation results of stress peak of cantilever beam experiment
实验结果表明,当结构不作阻尼处理时,在其各阶固有频率处容易发生共振,结构危险点应力急剧升高从而形成振动疲劳损伤,此时对结构进行约束阻尼处理能有效降低共振区域的响应幅值,且三层约束阻尼片要稍好于双层约束阻尼片的抑振效果。
5 结 论
(1)对于双层和三层的约束阻尼结构,三层结构具有更好的阻尼性能。
(2)通过仿真计算得到了针对悬臂梁结构的约束阻尼结构最佳参数分别为:阻尼层和约束层与悬臂梁厚度的比为1∶4,从根部铺设的长度不低于三分之二时效果最佳。
(3)通过本文设计的用于振动台同时夹持的夹具验证约束阻尼结构参数,在扫频试验过程中可知,约束阻尼结构能有效降低悬臂梁结构的共振响应,且三层约束阻尼结构的抑振效果更佳。
