不平衡电网电压下基于模块化多电平变流器的统一电能质量调节器的微分平坦控制
2021-08-29程启明马信乔赵淼圳
江 畅 程启明 马信乔 赵淼圳
不平衡电网电压下基于模块化多电平变流器的统一电能质量调节器的微分平坦控制
江 畅 程启明 马信乔 赵淼圳
(上海电力大学上海市电站自动化技术重点实验室 上海 200090)
电网电压不平衡时,电流电压波动较大,基于模块化多电平变换器(MMC)的统一电能质量调节器(UPQC)采用简单的PI控制难以调节电能质量。针对MMC-UPQC在电网电压不平衡的运行状态,提出一种基于正负序分离MMC-UPQC的微分平坦控制(DFBC)方法,它能够综合治理电压和电流的电能质量问题。首先,根据MMC-UPQC的拓扑结构,建立其在不平衡电网下的数学模型,分析MMC-UPQC的内部特性,验证MMC-UPQC的平坦性和稳定性;然后,根据正负序分离方法,采用无需锁相环方法对检测量进行分离,基于微分平坦控制理论,搭建结合前馈参考轨迹和误差反馈补偿的微分平坦控制器,并将其应用到多电平、高电压的MMC-UPQC电能质量补偿系统中,综合解决电网电压不平衡状态下的电网电能质量问题;最后,通过实验验证了基于所提微分平坦控制器的MMC-UPQC系统解决电压暂升、暂降和注入谐波问题的有效性和优越性。
模块化多电平变换器 统一电能质量调节器 不平衡电网电压 微分平坦控制 PI控制
0 引言
近些年,电力电子设备的大量投入,伴随着电网电压的暂升暂降、闪变、波动等非理想状态,电能质量下降。统一电能质量调节器(Unified Power Quality Conditioner, UPQC)[1-2]具有串联侧和并联侧两个部分,可以实现对电压、电流的电能质量综合补偿控制(也称综合治理),其灵活性和补偿多样性在提高电能质量方面得到广泛的应用和研究,但是,由于中高压电网的电压幅值较大,UPQC很难适用于高压配电网。模块化多电平变换器(Modular Multilevel Converter, MMC)具有耐压等级高、开关频率低的优势,其大电平数使得输出波形更加平滑完整,MMC自出现开始[3-4]一直在被研究并应用在多个领域,特别是直流输电[5-6],但是将MMC应用在UPQC的研究较少。电网电压不平衡时电压和电流的补偿和治理变得不理想,难以达到令人满意效果,而电网不平衡是很常见的电网状态。因此,对电网不平衡下MMC-UPQC的补偿控制策略的研究很有意义。
文献[7]采用PR控制,当电网电压不平衡或者受到扰动时,补偿效果欠佳。文献[8]研究了MMC的PI控制,控制参数难以确定并且反应速度较慢,动静态性能不佳。文献[9-10]研究了MMC并联侧的预测控制,控制方法对于结构复杂并且模块数较多的MMC,计算量增加且运行缓慢。文献[11-12]建立了一种MMC-UPQC并联补偿控制方式,它可以有效地补偿电流,但无法实现串联侧的补偿效果,同时没有涉及电压暂降情况的恢复,且鲁棒性很差。文献[13]提出MMC滞环电流控制,反应速度快,但当前命令的斜率在某个时间需要取而代之的是当前采样周期的斜坡,因此误差较大。文献[14]提出限幅电流协调控制,很好地处理了电压暂降的问题,但对于不理想状态下的控制没有更多的研究。文献[15]提出了一种无源控制,但是当系统参数发生变化时,控制器适应能力差,且该文献没有在高电压电网不平衡下研究。文献[16-18]提出针对电压不平衡条件下 MMC 的控制策略,但它们都仅考虑了如何保证三相电流对称,没有考虑电压不平衡的情况。文献[19]采用滑模无源性控制,虽然能够很好地解决电压不平衡问题,但将无源和滑模控制相结合使得控制器变得很复杂,且没有涉及并联侧电流不平衡时补偿方法。
综上所述,为了解决上述控制系统的不足并且实现系统的非线性控制,本文将微分平坦控制(Differential Flatness Based Control, DFBC)首次引入到在MMC-UPQC控制上。Fliess 在20世纪90年代针对非线性系统提出微分平坦理论,目前微分平坦控制理论已被应用于到电力电子变压器等控制中,文献[20-22]分别将微分平坦控制策略应用于逆变器、有源电力滤波器和MMC上,并获得了满意的控制效果。微分平坦控制无需精确的数学模型,可以根据输出变量的不同设计合适的前馈参考轨迹,通过误差反馈补偿更好地解决内部扰动和动静态特性问题。
为了实现MMC-UPQC更好的控制性能,在电网电压不平衡状态下,本文创新性地把DFBC引入MMC-UPQC中,分析了系统的平坦性和稳定性,设计了电网不平衡状态下基于MMC-UPQC的串联侧和并联侧微分平坦控制器。本文设计的MMC- UPQC微分平坦控制较文献[20-21]的区别在于:本文将微分平坦控制器应用于MMC-UPQC中,能够补偿和恢复负载侧电压和电网侧电流,但文献[20-21]只能控制MMC输出电流和直流侧电压,控制目标和电子元器件功能的不同使得本文设计的微分平坦控制器具有自身的独特性。本文所提的DFBC方法的动静态控制性能好,它能很好地解决MMC-UPQC补偿效果不佳的问题,提高电能质量,并通过实验验证了本文提出控制系统的有效性和优越性。
1 MMC-UPQC的拓扑结构和控制系统
1.1 MMC-UPQC的拓扑结构
图1为MMC-UPQC拓扑结构。UPQC的主电路各相桥臂由MMC构成,分为上、下桥臂,共有6个桥臂组成。每相上、下桥臂包含个子模块(Sub Module, SM)和1个电感器,每个子模块采用半桥结构。个SM可以输出+1个电平,电平数越多,谐波越小。每个SM由2个反并联二极管的IGBT半桥和1个电容组成,电容主要起到充放电作用。UPQC采用串联侧和并联侧MMC背靠背式的连接结构,中间采用大电容隔离,进行能量交换。串联侧变流器靠近电网侧,通过三个单相变压器接入电网,用以补偿电压的暂升、暂降和闪变等状态;并联侧变流器靠近负载侧,无需变压器直接接入电网,用以恢复电流的谐波以及不平衡状态。
图1中,a、b、c为电网三相电压,rk、gk为串联侧和并联侧MMC输出电压(下标r、g分别表示串联侧、并联侧,a, b, c),rk1为变压器一次电压,gk1为线路电压,rk为流入串联侧MMC电流,rk1、gk1分别为串联侧和并联侧的线路电流,rk2为流入串联侧电容电流,r、g为串联侧、并联侧的回路电感,1为两个变流器中间的直流侧电容,2为串联侧的并联电容,12为串联侧、并联侧的回路电阻。
1.2 MMC-UPQC的数学模型
根据MMC等效电路和基尔霍夫定律,由图1可得串联侧关系式为

图1 MMC-UPQC拓扑结构
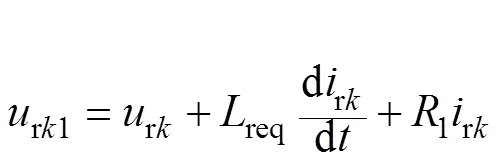

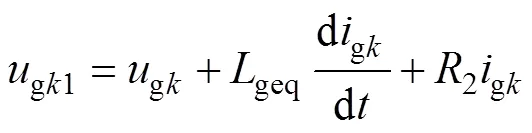
将式(1)、式(2)转化到dq旋转坐标系下,解耦后可得串联侧和并联侧的数学模型为
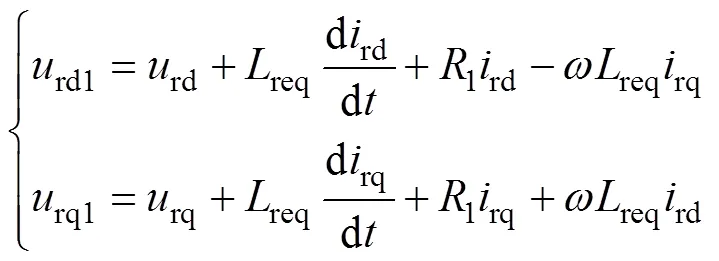
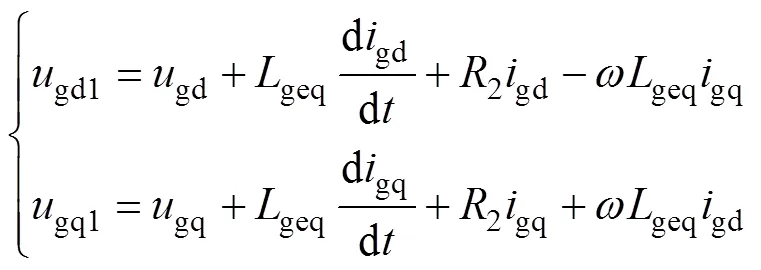
式中,为电网基波角速度,=2p=50Hz。
1.3 MMC-UPQC的PI双环控制结构
为了说明本文采用微分平坦方法控制MMC- UPQC的优势,在实验部分将其与当前最常用的PI控制方法相比较,且选取最优的PI参数。
由于正负序同型,以正序为例,MMC-UPQC的PI双环正序控制结构如图2所示。图中,外环的电压环控制可以根据所设定电压参考量,得出电流内环的d轴和q轴目标量;内环的电流环控制能够对电流d轴和q轴分量进行快速解耦和跟随给定,从而得到调制控制信号。
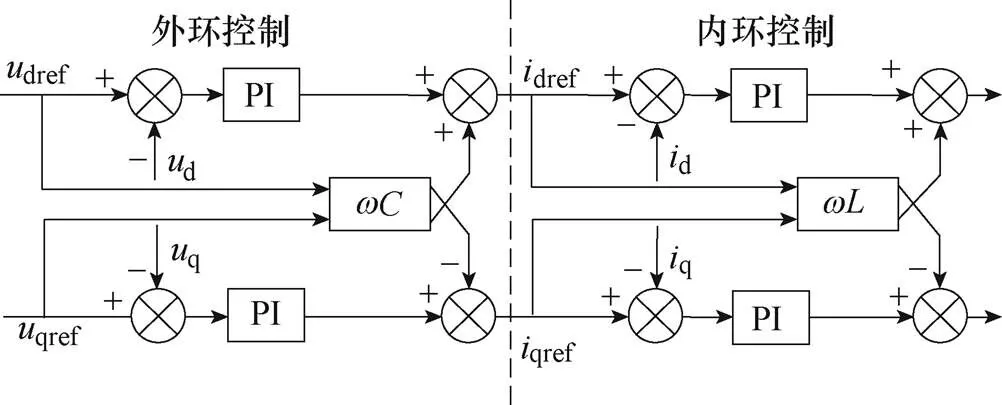
图2 MMC-UPQC的PI双环控制结构
图2中,d、q为dq旋转坐标系下的d、q轴电压分量;d、q为dq旋转坐标系下的d、q轴电流分量;dref、qref为设定的电压目标量;dref、qref为设定的电流目标量。
由于PI控制结构简单,适用于线性单变量对象控制,而电网电压不平衡状态下MMC-UPQC对象为非线性、多变量对象,因此这种复杂对象采用PI控制时,控制效果不会很好(存在稳定时间长、超调量大问题)。因此,本文提出一种适用于非线性对象的DFBC策略,并对MMC-UPQC串联侧和并联侧的外环和内环分别设计了DFBC非线性控制器。
1.4 环流抑制控制
当电网不平衡时,环流存在于MMC内部且比较严重,环流不仅会影响电力电子器件运行,且增大系统成本。为了保证波形准确,需要进行环流抑制,环流抑制控制框图如图3所示。本文采用的环流抑制方法为:先用低通滤波器(Low Pass Filter, LPF)滤出2倍频分量,再采用PI控制方法,将其环流控制到0,这样不仅省去了正负序分离,而且可以快速地将各桥臂的环流分量去除。图中,dcir是环流的d轴分量,qcir是环流的q轴分量。

图3 环流抑制控制框图
1.5 直流侧电容电压控制
本文采用MMC-UPQC背靠背式连接结构,其中串联侧、并联侧的MMC中间直流侧连接处采用大电容连接,称之为直流母线电容。直流母线电容作为电压补偿单元和电流补偿单元之间进行能量交换的介质,直流侧电容两端电压大小影响桥臂和子模块电容电压,因此直流侧电容上电压的控制也很重要。
直流侧电容电压采用PI控制,直流侧电容电压通过PI控制器紧紧跟随设定值,PI控制后的信号与外环控制得到的补偿电流相结合进入内环控制器,在系统产生补偿电流的同时对直流侧电容电压进行控制。直流侧电容电压控制框图如图4所示,其原理是将采集来的电压信号进行滤波处理,正负序分离后通过PI控制将其稳定在期望值,获得直流侧电容电压的控制电流信号ct,再进入内环的微分平坦控制,得到控制信号cd,这样控制信号中就包括对电容电压的控制,确保直流侧电容电压的稳定。图4中,dcref为直流侧电容电压参考值,ct为经PI控制后的控制量。
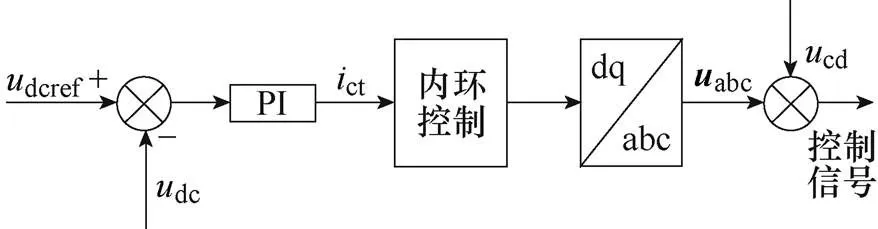
图4 直流侧电容电压控制框图
2 MMC-UPQC的微分平坦治理新策略
2.1 微分平坦原理



且式(5)、式(6)中的、为正整数,输出的各阶导数独立,说明此系统为微分平坦系统。但是输出变量的选取不是唯一的,根据输出变量的不同控制器的设计也不一样。
图5为微分平坦控制系统框图。微分平坦理论的控制器设计主要分期望前馈参考轨迹生成和误差反馈补偿两个部分。期望前馈参考轨迹生成是根据期望的输出变量,规划状态空间中变量的参考运动轨迹,再根据MMC-UPQC的数学模型,产生前馈参考轨迹的控制量,但电压波动和内部扰动对系统的稳定性影响较大,使前馈控制量难以达到期望输出,为了减小影响,需要加入误差反馈补偿,需要通过输出量和期望值形成误差反馈D,结合误差反馈设定值Dy对参考轨迹生成的控制量进行补偿。

图5 微分平坦控制系统框图
2.2 MMC-UPQC的平坦性
将式(3)、式(4)的串联部分和并联部分相结合,可得MMC输出侧的dq坐标模型为
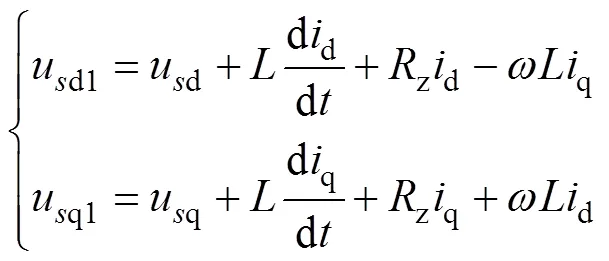
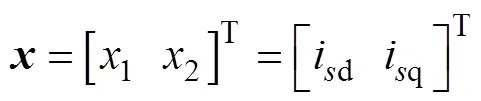

根据式(7)可知,输入变量为

无功功率瞬时值为
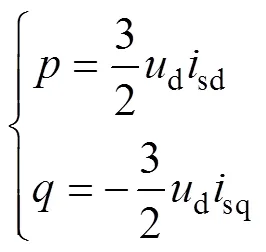


由式(8)、式(9)、式(11)和式(12)可知,不论模式1还是模式2下,MMC-UPQC的状态变量和输入变量都可以由输出变量及其导数表示,由微分平坦理论和式(5)、式(6)说明,在这两种模式下系统具有平坦性。
2.3 MMC-UPQC微分平坦系统稳定性证明
本文的误差反馈采用PI控制器,将平面输出的比例积分误差定义为

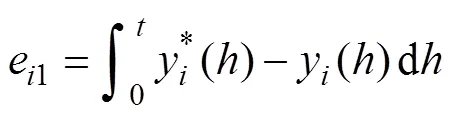

对式(15)求导得可得
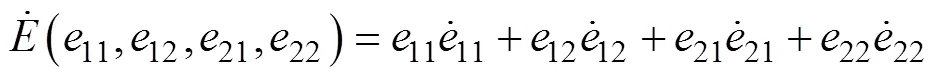
结合式(4)、式(9)和式(12),可得

通过使基于平面输出的Lyapunov函数全局渐近稳定,将所提出的控制输入表示为
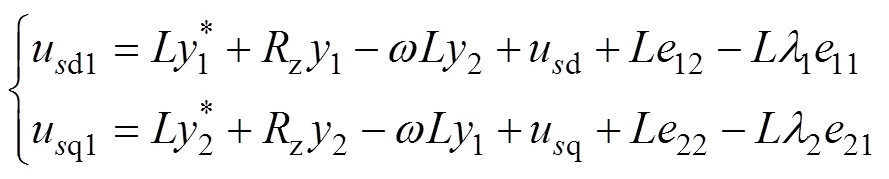
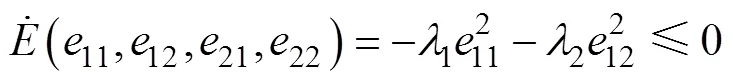
根据Lyapunov稳定性原则可知,系统是渐近稳定的,使用PI控制器可以跟随期望,达到稳定。
3 MMC-UPQC的微分平坦控制器设计和综合治理
MMC-UPQC的微分平坦控制器分为两个部分:①根据输出变量确定期望前馈参考轨迹;②减小内部扰动设计误差反馈补偿。本文提出的基于微分平坦理论的MMC-UPQC控制器由串联侧控制器和并联侧控制器两部分组成,每个控制器都采用双环 控制。
3.1 MMC-UPQC串联侧控制器设计
MMC-UPQC的串联侧控制器包括电压外环和电流内环。
1)串联侧内环微分平坦控制器的设计
根据式(7),可得串联侧内环控制器期望前馈参考控制量为
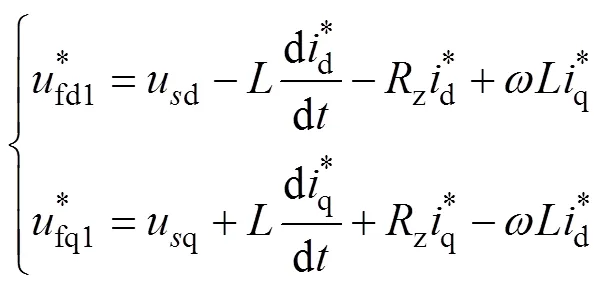
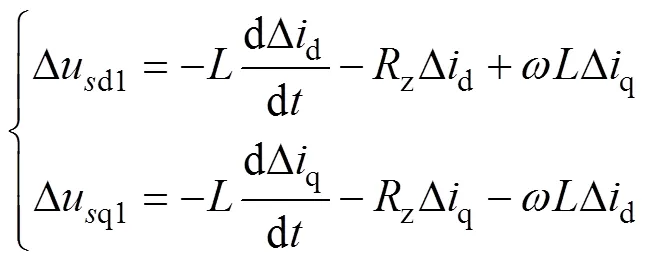
对式(21)进行拉普拉斯变换,可得
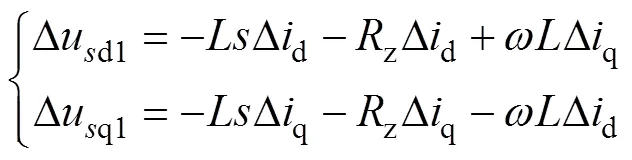
本文误差反馈补偿采用PI控制器进行线性化,由式(22)可得闭环传递函数,并由闭环传递函数得PI控制误差补偿非线性数学模型为
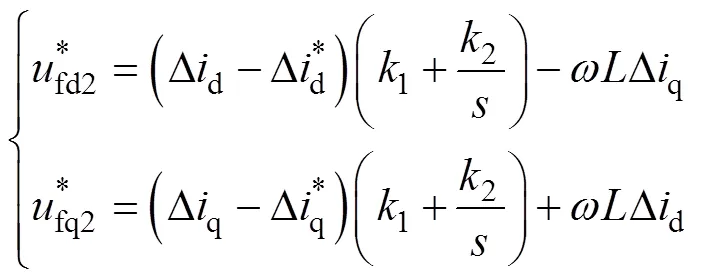

2)串联侧外环微分平坦控制器的设计
根据串联侧基尔霍夫定律可得

将式(25)变换到dq坐标系下得到



同内环电流PI控制推导,由式(28)得闭环传递函数,由闭环可得串联侧外环的PI误差补偿为
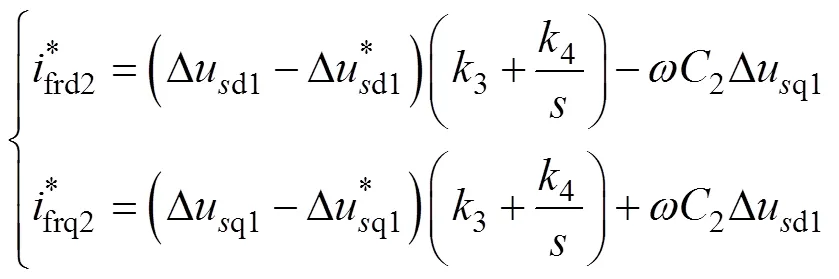
的比例系数和积分系数。为了消除误差,可令误差为0,可得串联型外环输出参考值为
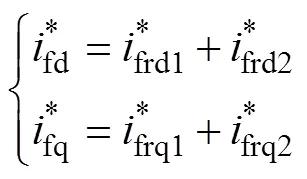
3.2 MMC-UPQC并联侧控制器设计
MMC-UPQC的串联侧控制器包括有功无功外环和电流内环。同理,可得并联侧外环控制器期望前馈参考控制量为


同串联侧推导,由式(32)得闭环传递函数,可得采用PI控制的非线性误差数学模型为
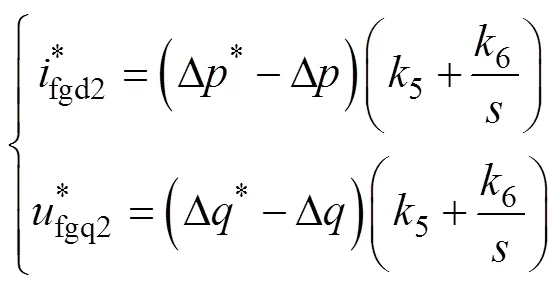
器的比例系数和积分系数。为了消除误差,可令其为0,得串联型外环输出参考值为
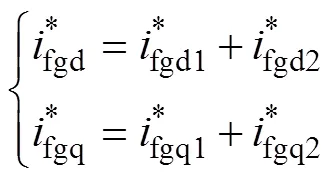
MMC-UPQC串联侧和并联侧的内环均为电流环,根据式(7),可得并联侧与串联侧内环微分平坦控制器相同。
3.3 MMC-UPQC微分平坦控制系统结构
图6为电网电压不平衡状态下MMC-UPQC微分平坦控制系统框图。由图6可见,控制系统主要由串联侧内外环控制器、并联侧内外环控制器、正负序分离、参考值获取、直流侧电容电压控制器、电容均压控制、环流抑制控制和载波移相调制等部分组成。其工作原理是:利用锁相环,从系统提取的电压、电流检测值,经过正负序分离后生成参考量,根据式(23)、式(28)和式(31)设计串联侧和并联侧的DFBC控制器对MMC-UPQC进行微分平坦控制,结合直流侧电容电压控制、电容均压控制和环流抑制控制,产生调制波进入载波移相调制,获得脉冲信号控制MMC运行,进而达到恢复电压和电流的效果。

图6 电网电压不平衡下MMC-UPQC微分平坦控制框图
4 实验分析
为了说明MMC-UPQC采用本文的微分平坦控制的优势,把微分平坦控制与PI控制两种方法,针对电网电压发生暂升、暂降和注入谐波变成不平衡状态的情况进行实验比较。此次实验设置的电网电压为10kV,以此来验证MMC-UPQC子模块耐压性能,可否用于高压电网。
本文MMC-UPQC系统的实验参数见表1。
表1 实验参数

Tab.1 Simulation parameters
4.1 串联侧MMC的电压补偿实验
当电网电压不平衡时,即a相电压在0.02s发生20%的暂升,0.08s暂升结束且在0.12s又发生20%的暂降,0.18s暂降结束,在此情况下两种控制方法实验比较如图7所示。
由图7可见,当电网电压发生暂升时,微分平坦控制的反应速度相对于PI控制更迅速,在0.01s内能够将电网电压恢复至1kV并稳定,但是PI控制需要0.05s。当发生电网电压暂降时,PI控制需要0.02s达到期望,而微分平坦控制仅需0.013s。总体上微分平坦控制比PI控制的电压波动更小,微分平坦控制超调量为0.011%,而PI控制为0.023%。进一步对谐波失真度分析,暂降状态时,微分平坦控制器总谐波畸变率(Total Harmonic Distortion, THD)为1.85%,而PI控制器THD=5.24%。因此,串联侧MMC-UPQC采用微分平坦控制电压补偿的快速性和稳定性更好。

图7 电网电压不平衡时串联侧MMC的两种电压补偿方法实验比较
为体现处理电网电压谐波能力,注入幅值为2 500V(为电网电压幅值的25%)的3次谐波,此时THD=23.68%,电网电压注入谐波时串联侧MMC的两种电压补偿方法实验比较如图8所示。
由图8可见,当0.05s时,由于注入谐波,电网电压波形发生明显变化,微分平坦控制不到1个周期达到控制目标,约为0.018s,而PI控制只能减小THD,无法很好地补偿谐波。经过控制器的补偿,微分平坦控制后的THD=4.38%,PI控制后的THD= 8.12%,并且从补偿量的角度来看,0.05s时微分平坦控制补偿量已经稳定,但PI控制一直在波动。因此,微分平坦控制的整体补偿效果要比PID控制好得多,且能够更快速、准确地补偿电压。
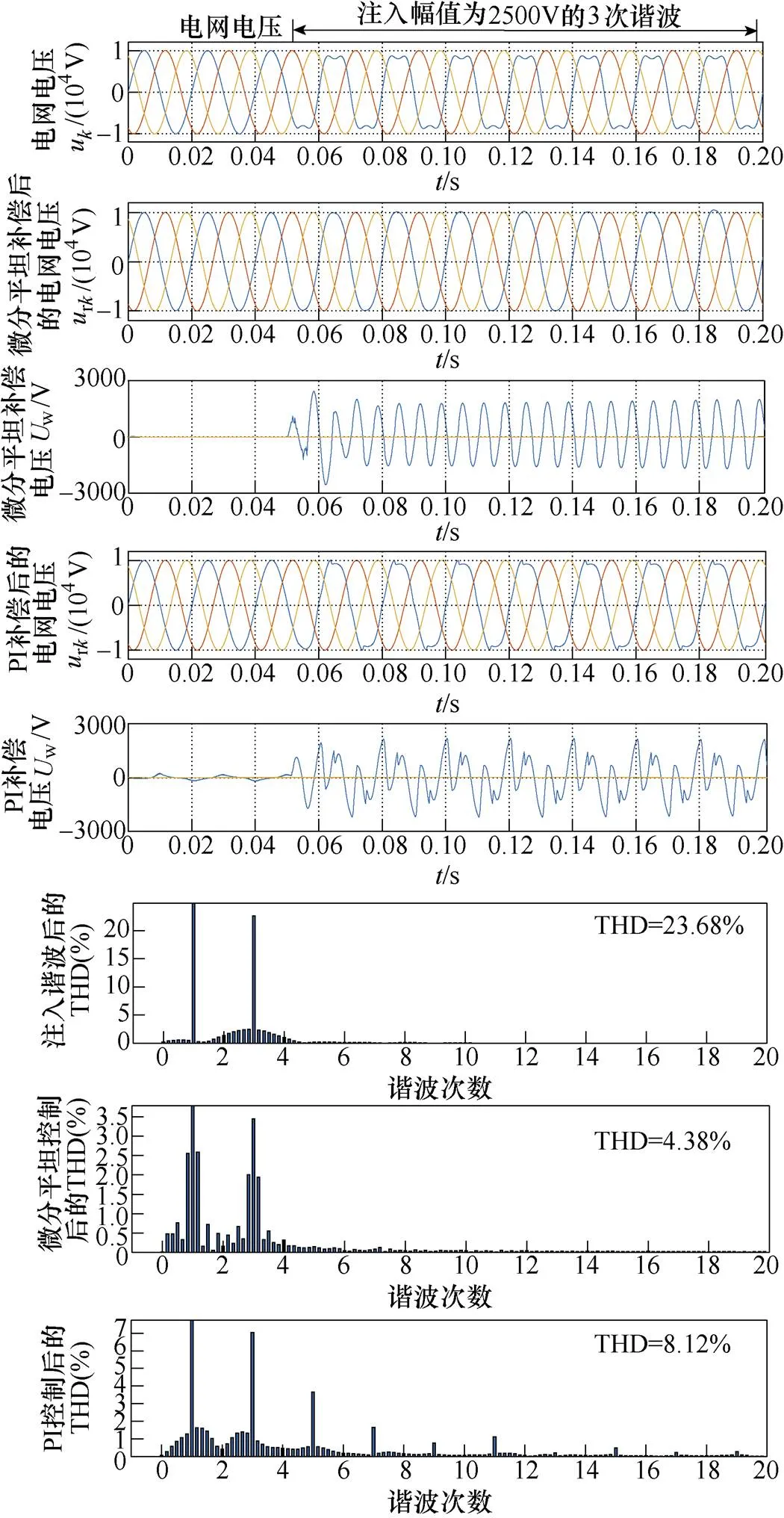
图8 电网电压注入谐波时串联侧MMC的两种电压补偿方法实验比较
4.2 并联侧MMC的电流补偿实验
本文并联侧MMC的非线性负载采用一个电阻3和一个IGBT串联,再通过RL缓冲电路与阻感负载串联,并联侧MMC的非线性负载电路如图9所示。
当并联侧MMC负载为非线性负载时,电流含有大量的谐波,且谐波失真度大,THD=26.53%,非线性负载时并联侧MMC的两种电流补偿方法比较如图10所示。

图9 并联侧MMC的非线性负载电路

图10 非线性负载时并联侧MMC的两种电流补偿方法比较
由图10可见,微分平坦控制在0.009s时电流稳定,而PI控制在0.027s时电流稳定,且PI控制波动较大,电流幅值一直处于一个不断衰减的过程,而微分平坦控制更加稳定。总体来看,微分平坦控制效果更好,微分平坦控制和PI控制都可以补偿电流谐波,但微分平坦控制THD=2.34%,PI控制THD= 7.17%。因此,并联侧MMC采用微分平坦控制时,恢复电流更加平滑,反应时间和动态过程更佳。
当电网电压发生暂升和暂降时,对负载电流的影响也很大,能否恢复暂升暂降情况下的谐波电流十分关键。图11为电网电压变化时并联侧MMC的两种电流补偿方法比较。
由图11可见,在电网电压暂升时,微分平坦控制可以快速跟随,0.013s内即可快速达到平衡,但PI控制反应较慢,需要约2个周期的时间,约为0.04s。在电网电压暂降时,分析两种控制方式的超调量和THD。DFBC控制超调为0.01%,PI为0.017%,微分平坦控制THD=3.58%,PI控制THD=7.15%。由此可得,微分平坦控制相对于PI控制,其超调量更小,且谐波失真度和脉动较小,能达到更好的控制效果。

图11 电网电压变化时并联侧MMC的两种电流补偿方法比较
为了深入研究本文设计的微分平坦控制对电流的恢复能力,在非线性负载产生谐波的基础上,在0.05s注入幅值为2 500V的3次谐波,负载电流注入谐波时并联侧MMC的两种电流补偿方法比较如图12所示。

图12 负载电流注入谐波时并联侧MMC的两种电流补偿方法比较
由图12可见,在注入谐波之后,电流波形畸变更厉害,THD=26.8%。对于控制器的要求更高。微分平坦控制依然能快速恢复,约在0.014s能够恢复电流。但是PI控制没有产生足够的补偿量,因此无法完全补偿谐波量,导致补偿效果不佳,不能很好地发挥作用。微分平坦控制下THD=2.76%,PI控制下THD=9.36%。因此,当发生谐波干扰时,微分平坦控制补偿能力更强、效果更佳。
5 结论
本文针对电网不平衡下MMC-UPQC系统运行问题,结合微分平坦控制策略,设计补偿控制器,即在检测值正负序分离后,将微分平坦控制用于MMC-UPQC的串联侧和并联侧电能质量调节。通过本文研究可以得到结论:
1)MMC-UPQC的数学模型适用于采用微分平坦控制理论,本文设计的串联侧和并联侧微分平坦控制器具有平坦性、平滑性和稳定性。针对中高压电网不平衡状态,它能很好地解决电能质量综合补偿问题。
2)MMC-UPQC的微分平坦控制方法相比于PI控制方法,优势非常明显,补偿时间快70%左右,且总谐波畸变率小于5%,其调节速度更快、鲁棒性更强、控制效果更佳。
3)针对电网电压的谐波、不平衡及电流的不平衡、谐波、非线性问题,本文提出的MMC-UPQC微分平坦控制系统均有很好的补偿效果。实验结果证明了本文所提出的微分平坦控制系统对电压和电流补偿的有效性和优越性。
[1] 黄晓明, 范志华, 苗世洪, 等. 含储能单元的统一电能质量调节器功率协调控制策略[J]. 高电压技术, 2018, 44(10): 3390-3398.
Huang Xiaoming, Fan Zhihua, Miao Shihong, et al. Coordinated power control strategy of unified power quality conditioner with energy storage unit[J]. High Voltage Engineering, 2018, 44(10): 3390-3398.
[2] Ghosh A, Ledwich G. A unified quality conditioner for simultaneous voltage and current compensation[J]. Electric Power Systems Research, 2001, 59(1): 55-63.
[3] 王兴贵, 薛晟, 李晓英. 模块化多电平变流器半桥串联结构微电网输出特性分析[J]. 电工技术学报, 2019, 34(10): 2130-2140.
Wang Xinggui, Xue Sheng, Li Xiaoying. Analysis of output characteristics of a microgrid based on modular multilevel converter half-bridge series structure[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2130-2140.
[4] 申科, 王建赜, 班明飞, 等. 基于阶梯波调制的MMC电容电压平衡控制方法对比研究[J]. 电机与控制学报, 2016, 20(10): 1-8.
Shen Ke, Wang Jianze, Ban Mingfei, et al. Com- parative analysis on capacitor voltage balance control strategies for staircase modulated modular multilevel converter[J]. Electric Machines and Control, 2016, 20(10): 1-8.
[5] 郑安然, 郭春义, 殷子寒, 等. 提高弱交流系统下混合多端直流输电系统小干扰稳定性的控制参数优化调节方法[J]. 电工技术学报, 2020, 35(6): 1336-1345.
Zheng Anran, Guo Chunyi, Yin Zihan, et al. Optimal adjustment method of control parameters for improving small-signal stability of hybrid multi- terminal HVDC system under weak AC condition[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1336-1345.
[6] 董鹏, 蔡旭, 吕敬. 不对称交流电网下MMC- HVDC系统的控制策略[J]. 中国电机工程学报, 2018, 38(16): 4646-4657, 4970.
Dong Peng, Cai Xu, Lü Jing. Control strategy of MMC-HVDC system under asymmetric AC grid conditions[J]. Proceedings of the CSEE, 2018, 38(16): 4646-4657, 4970.
[7] Ghetti F T, Ferreira A, Braga H A C, et al. A study of shunt active power filter based on modular multilevel converter (MMC)[C]//2012 IEEE transactions on industry applications, New York, 2012: 1-6.
[8] Bergnadiaz G, Zonetti D, Sanchez S, et al. PI passivity-based control of modular multilevel con- verters for multi-terminal HVDC systems[C]//IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, 2017: 523-528.
[9] Shu Zeliang, Liu Ming, Zhao Li, et al. Predictive harmonic control and its optimal digital implementation for MMC-based active power filter[J]. IEEE Transa- ctions on Industrial Electronics, 2016, 63(8): 5244- 5254.
[10] Sun Yuanxiang, Li Zhen, Zhang Zhenbin. Hybrid predictive control with simple linear control based circulating current suppression for modular multilevel converters[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 335-341.
[11] Cao Wu, Liu Kangli, Wu Mumu, et al. An improved current control strategy based on particle swarm optimization and steady-state error correction for SAPF[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 4268-4274.
[12] 程启明, 孙伟莎, 程尹曼, 等. 电网电压不平衡下MMC的无源控制策略[J]. 电力自动化设备, 2019, 39(4): 78-85.
Cheng Qiming, Sun Weisha, Cheng Yinman, et al. Passive control strategy of MMC under unbalanced grid voltage[J]. Power Automation Equipment, 2019, 39(4): 78-85.
[13] 鲍禄山. 并联APF谐波电流控制算法的研究[D]. 成都: 西南交通大学, 2016.
[14] 陆晶晶, 肖湘宁, 张剑, 等. 基于定有功电流限值控制的MMC型UPQC协调控制方法[J]. 电工技术学报, 2015, 30(3): 196-204.
Lu Jingjing, Xiao Xiangning, Zhang Jian, et al. MMC-UPQC coordinated control method based on fixed active current limit value control[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(3): 196-204.
[15] 祝贺, 王久和, 郑成才, 等. 五电平MMC-UPQC的无源控制[J]. 电工技术学报, 2017, 32(增刊2): 172-178.
Zhu He, Wang Jiuhe, Zheng Chengcai, et al. Passivity based control of five-level MMC-UPQC[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(S2): 172-178.
[16] 易灵芝, 黄晓辉, 黄守道, 等. 基于最近电平逼近调制的模块化多电平变换器中高压变频调速系统运行控制[J]. 电工技术学报, 2020, 35(6): 1303-1315.
Yi Lingzhi, Huang Xiaohui, Huang Shoudao, et al. A medium-voltage motor drive with modular multilevel converter based on nearest level modulation[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1303-1315.
[17] 王振浩, 张震, 李国庆. 基于补偿原理的MMC- HVDC系统不对称故障控制策略[J]. 电力系统自动化, 2017, 41(17): 94-100.
Wang Zhenhao, Zhang Zhen, Li Guoqing. An unba- lanced fault control strategy for MMC-HVDC system based on compensation principle[J]. Automation of Electric Power Systems, 2017, 41(17): 94-100.
[18] 梁营玉. 不对称电网电压下基于降阶矢量谐振器的MMC-HVDC直接功率控制策略[J]. 中国电机工程学报, 2017, 37(24): 7294-7303.
Liang Yingyu. Direct power control strategy based on reduced order vector resonant controller for MMC- HVDC under unbalanced grid voltages[J]. Proceedings of the CSEE, 2017, 37(24): 7294-7303.
[19] 柯顺超, 朱淼, 陈阳, 等. 基于MMC-UPFC无源性滑模变结构控制的电网不平衡治理策略[J]. 高电压技术, 2020, 46(3): 1077-1085.
Ke Shunchao, Zhu Miao, Chen Yang, et al. Treatment strategy of unbalanced grid voltage conditions based on MMC-UPFC passive sliding-mode variable structure control[J]. High Voltage Engineering, 2020, 46(3): 1077-1085.
[20] 宋平岗, 吴继珍, 邹欢, 等. 模块化多电平换流器功率平坦控制策略[J]. 电网技术, 2016, 40(2): 563-570.
Song Pinggang, Wu Jizhen, Zou Huan, et al. Power flatness control strategy for modular multilevel converter[J]. Power System Technology, 2016, 40(2): 563-570.
[21] 宋平岗, 李云丰, 王立娜, 等. 基于微分平坦理论的模块化多电平换流器控制器设计[J]. 电网技术, 2013, 37(12): 3475-3481.
Song Pinggang, Li Yunfeng, Wang Lina, et al. Differential flatness based design of controller for modular multilevel converter[J]. Power System Technology, 2013, 37(12): 3475-3481.
[22] Mehrasa M, Pouresmaeil E, Taheri S, et al. Novel control strategy for modular multilevel converters based on differential flatness theory[J]. IEEE Journal of Emerging and Selected Topics in Power Electro- nics, 2018, 6(2): 888-897.
Differential Flat Control for Unified Power Quality Controller Based on Modular Multilevel Converter under Unbalanced Grid Voltage
(Shanghai Key Laboratory of Power Plant Automation Technology Shanghai University of Electric Power Shanghai 200090 China)
When the grid voltage is unbalanced, the current and voltage fluctuate greatly, and the unified power quality controller (UPQC) based on modular multilevel converter (MMC) is difficult to adjust power quality with simple PI control. Aiming at the unbalanced operating state of MMC-UPQC in the power grid voltage, this paper proposes a differential flat control (DFBC) method based on positive and negative sequence separation, which can comprehensively manage the power quality problems of voltage and current. Firstly, according to the topology of MMC-UPQC, the mathematical model under unbalanced power grid is established by analyzing the internal characteristics of MMC-UPQC, and the flatness and stability of MMC-UPQC are verified. Then, the detection quantity is separated without phase-locked loop through a method of positive and negative sequence separation. Based on the differential flat control theory, a differential flat controller that combines feedforward reference trajectory and error feedback compensation is built and applied to a multi-level, high-voltage power quality compensation system,which can solve the grid power quality problem under the unbalanced grid voltage. Finally, the experiment verifies the effectiveness and superiority of the MMC-UPQC system based on the proposed differential flat controller in solving the problems of voltage rising, sagging and injected harmonic.
Modular multilevel converter, unified power quality controller, unbalanced grid voltage, differential flatness based control, PI control
10.19595/j.cnki.1000-6753.tces.200672
TM711
江 畅 男,1996年生,硕士研究生,研究方向为电力系统自动化、有源电力滤波器等。E-mail: 1009722953@qq.com!!
程启明 男,1965年生,博士,教授,硕士生导师,研究方向为电力系统自动化、发电过程控制、先进控制及应用。E-mail: chengqiming@sina.com(通信作者)
国家自然科学基金项目(61905139)和上海市电站自动化技术重点实验室项目(13Z2273800)资助。
2020-06-20
2020-09-26
(编辑 陈 诚)
