等离子体鞘套局部电磁传输通道法*
2021-08-29杨鑫
杨 鑫
(1.贵州大学 大数据与信息工程学院,贵州 贵阳 550025;2.半导体功率器件可靠性教育部工程研究中心,贵州 贵阳 550025;3.贵州省微纳电子与软件技术重点实验室,贵州 贵阳 550025)
0 引言
等离子体鞘套建模是高超音速飞行领域的重要问题,只有获取可靠的鞘套模型,才能全面了解和掌握鞘套的电磁传输特性,进一步为缓解通信黑障提供条件[1-3]。但多年来,因受制于实验条件,人们主要从仿真角度研究鞘套建模问题[4-6]。这些研究的出发点是Navier-Stokes方程,结合具体条件解该方程,获得鞘套数值模型。此方法的优势在于,摆脱了物理实验对研究的束缚,同时易于研究各种环境下鞘套的基本特征。可是它也有不足之处,譬如,难以模拟实际高超音速飞行环境,且仿真模型往往限于钝头和尖头等简单小尺度几何模型[7]。实际上,自21 世纪70 年始,美国在高超音速方面开展了一系列飞行实验[8-9],所得数据目前已对公众开放,只是实验采集的仅有一维数据,这种数据形式无疑限制了它的应用范围。因此,主要在研究鞘套的一维传输特性时[10-12],这些数据才有被用到。
然而在特定条件下,一维数据往往也包含三维信息,用它可近似还原目标三维模型。这正是本文关注的主要问题,并将其用于电磁传输特性分析。首先,根据鞘套局部区域具有相似性的特点,给出一种反演建模法,由鞘套一维数据反演三维传输通道。在此基础上,利用非均匀介质射线跟踪法,研究鞘套对电波能量传输的影响,重点揭示L 和S 这一卫星通信和雷达工作波段的传播行为。本文中所给方法为鞘套建模提供一新思路,研究结果可增进对鞘套电磁传输干扰的理解。
1 鞘套局部特征建模
实验数据通常满足某种函数关系,可选用不同数学形式进行描述,数学形式的选用直接影响后续计算的复杂程度。针对鞘套模型,本文以文献[13]一维径向电子密度分布实验数据为基础,选用指数函数对其拟合后,结果如下:
n(x)=a+bcx(1)
其中,参数a、b 和c 分别取值4.396 91×1 017、1.904 5×1 019 和1.849 06×10-5。考虑实际情形,鞘套局部范围往往具有类似分布,在数学上满足近似的函数关系。所以从局部近似角度考虑,一维分布函数可表征鞘套局域特征,这是反演建模的基础。图1(a)给出了本文关注的鞘套局域示意,即“仿真窗口”。只要该窗口物理尺度选取恰当,内部会遵循相似分布,这种分布就可由一维数据反演。图1(b)为仿真窗口的几何模型。因鞘套边界必然与飞行器外形相关,为使它的空间分布更贴近实际情形,本文在式(1)基础上,引入电子密度伸缩因子β,使鞘套边界特征与飞行器表面吻合。此时,经式(1)反演后,鞘套轴向剖面局部分布如下:
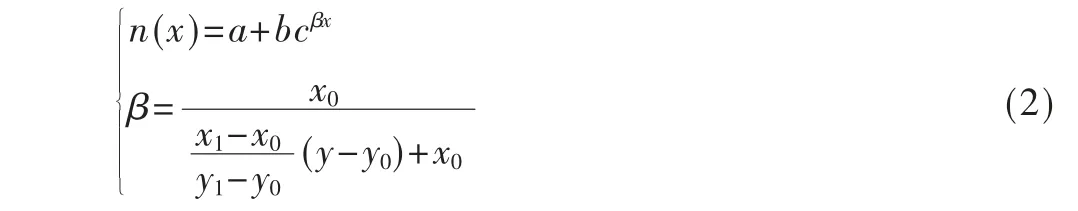
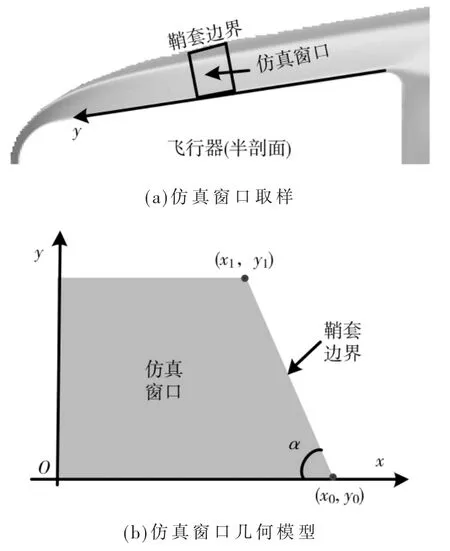
图1 鞘套几何分布图
因需在球坐标系下求解方程,针对固定剖面譬如φ=0,式(3)球坐标形式为:
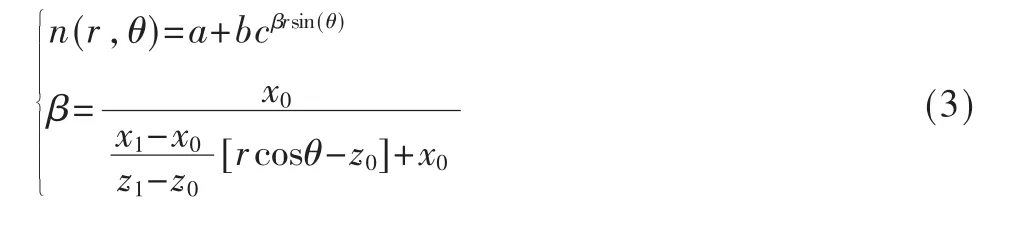
为便于后续计算,坐标轴y 已用z 代替。如图1(a)所示,伸缩因子本质是:模拟鞘套实际边界,保证仿真窗口在满足边界条件同时,区域内数据还能够遵循相似分布。再如图1(b)所示,在边界点(x0,y0)与(x1,y1)已知情形下,可得鞘套边界满足方程:

式(4)同样可变换为球坐标表述形式。只是对于复杂外形飞行器,鞘套边界往往比较复杂,边界条件也就需根据具体环境进行设定。
最后,根据上述结果,可计算鞘套的局部特征分布,如图2 所示。图2(a)为式(1)计算结果,并与实验数据对比,展示出函数的良好拟合性。图2(b)是根据式(2)建立的鞘套局部仿真窗口,计算中,(x0,y0)和(x1,y1)的取值分别为(1.2,0.0)以及(1.0,0.4)。图2(b)显示,沿飞行器表面方向,鞘套电子密度分布呈压缩趋势,这就较为真实地体现出它的空间分布特征。若再结合必要的建模手段,则反演结果可更加真实反映模型在局部区域的物理特征。
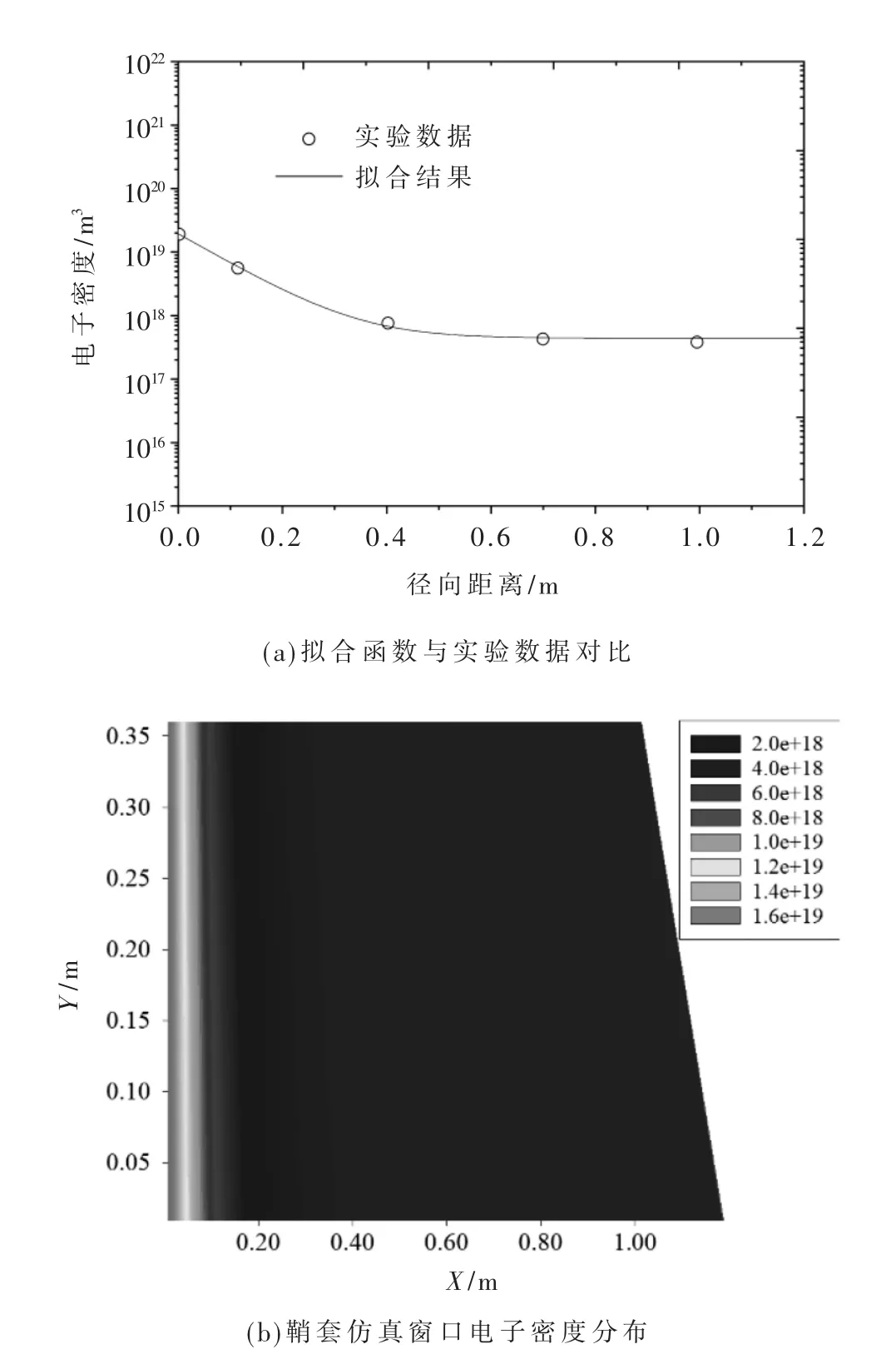
图2 实验数据的提取与建模
2 等离子体中的射线跟踪法
高超音速飞行器鞘套实质上是等离子体薄层,故可用等离子体中电波传播原理求解相关问题。高频情形下,电波行为可由射线方程描述[14]:
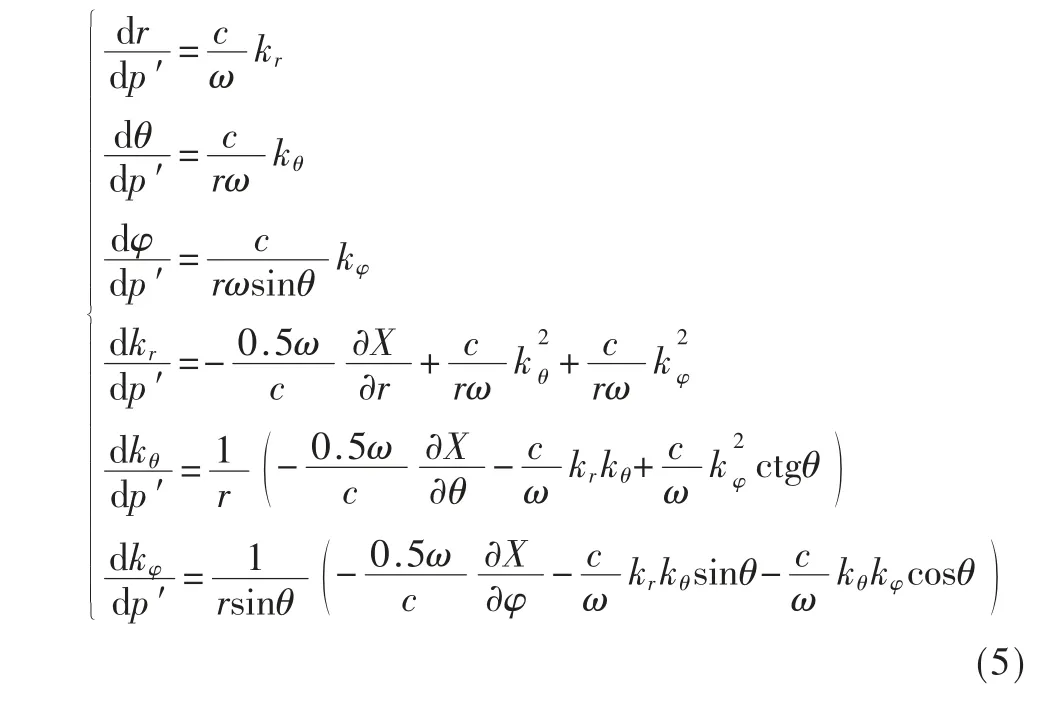
式中,p′为电磁射线积分路径;c 为自由空间中电波传播速度;r、θ和φ表示球坐标系空间坐标值,kr、kθ和kφ是波矢量在球坐标系中的分量。而X 代表折射率的分布函数:

其中,n(r,θ)为鞘套折射率空间分布,可根据介电常数计算。对于等离子体这类物质,介电常数的计算模型为:
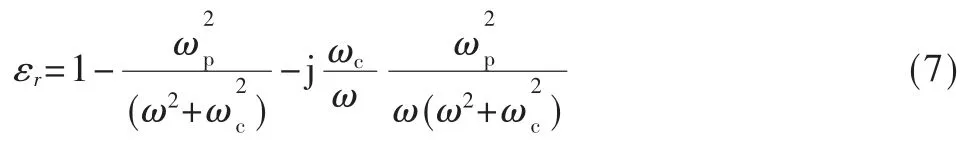
式中,ωp代表等离子频率,ωc为等离子体碰撞频率。结合式(6)和式(7)求解式(5),获得电波在鞘套内各方向的传播轨迹,进一步便可分析其对电波的干扰机制。本文主要关注它在电波能量传输方面的影响。设射线起始点为P0,终点为P1,电波在两点间的衰减情况Att(dB)可由下式得到:

其中,E0表示电波的初始振幅,E 为观察点处的场值。该式的物理意义为:若将电磁轨迹分为若干单元dr,则沿轨迹的整体衰减等于每dr 单元衰减的叠加。前述方程的数值解法请见文献[15]。
3 鞘套的电磁传输特性
根据RAM-C 飞行实验数据,采用反演建模法构建鞘套模型;然后,结合非均匀介质电波传播原理与射线跟踪法,分析S 和L 波段部分频点电波在鞘套中的传播行为,计算结果如图3 和图4 所示。图中射线方向以图1飞行器表面为参照,沿表面正向取作0°。结果显示,鞘套对电波行为影响明显,并显示出一些新的现象。
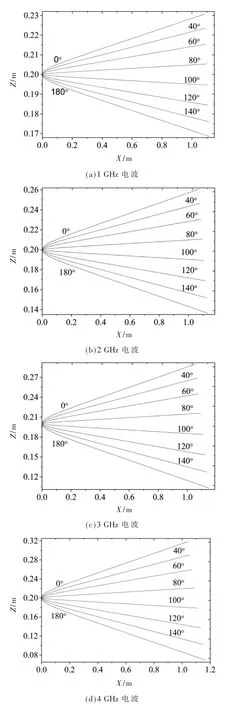
图3 电波在鞘套中的传输轨迹
首先,如图3 所示,电波表现出沿特定方向传播的行为,这种行为随频率增加而减弱,该现象可由鞘套电子浓度分布解释。图2 显示,沿飞行器径向,电子浓度呈逐渐降低趋势,这一趋势在距飞行器表面0.0~0.3 m 处更显著。正是电子浓度上述特征,导致电磁射线趋于90°方向传播;而后在约大于0.3 m 范围,因电子密度空间变化率相对较小,射线直线特征逐渐增强。对比图3(a)和图3(d),随着频率增加,鞘套对电波行为的影响减弱,沿特定方向传播的趋势亦随之减弱。这些现象表明,若仅从传播方向角度考虑,本文关注的鞘套模型会有助于电波传播。另外,在1 GHz 时,射线分布呈良好对称性;但随着频率增加,如4 GHz 时,对称性逐渐消失;这同样可由鞘套空间分布特征来揭示。如图2(b)所示,鞘套电子密度的空间变化率分布具有沿轴向(飞行器头部)增强的趋势,它使得在0°~90°方向传播的射线受鞘套影响更加明显;并且随着电波频率增加,这种差异会更加显著,最终导致电波在传输方向上对称性的消失。
最后,给出与图3 相应频点电波在透过鞘套后的衰减情况,如图4 所示。总体来看,鞘套对L 和S 波段显示出类似的衰减趋势:沿飞行器头部方向传播的射线,传输效率更高;而尾部方向所受干扰最为强烈。该现象与鞘套边界空间分布相关:沿头部方向传播的射线穿过较短的高密度鞘套域,故受鞘套影响相对较小。这些结果表明,因L 波段衰减强烈,已不适用于这种通信环境;而S 波段穿透鞘套的能力较强,所以更有可能满足这种环境下的通信需求。
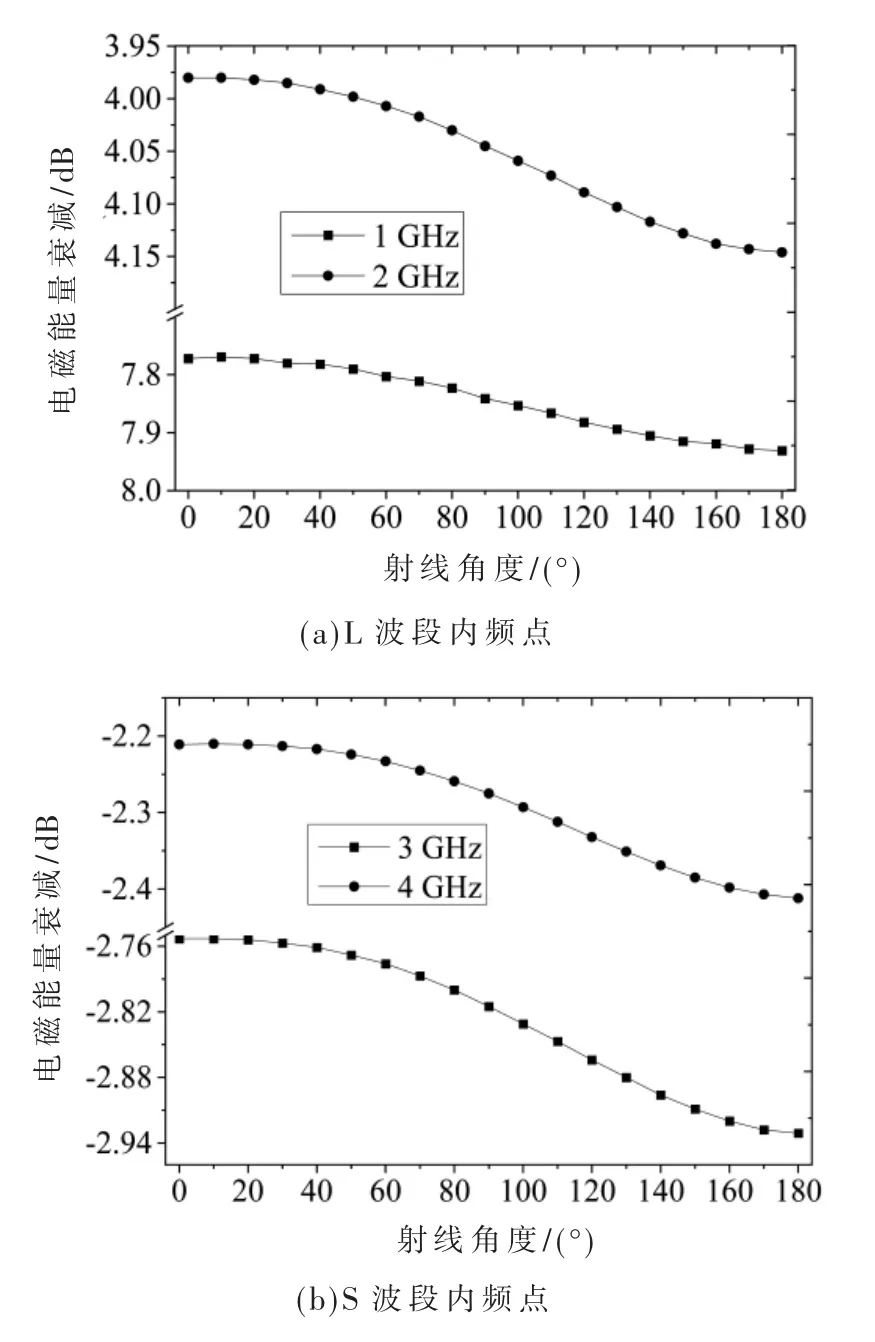
图4 电波在鞘套中的衰减情况
4 结论
本文以高超音速实验数据为基础,给出一种反演建模法并用于鞘套电磁建模;后采用非均匀介质电波传播原理与射线跟踪法,揭示鞘套对L 和S 电波段传输的影响,并获得一些新结果。研究显示,本文所关注鞘套模型具有使电波沿特定方向传播的特征,但该特征会随着电波频率增加而减弱;另外,电波沿飞行器头部方向传播能力最强,向尾部传播能力反之。研究还表明,因S 波段总体上受鞘套的干扰较弱,可为该飞行场景下的正常通信提供条件。这些结果也会有助于促进对鞘套在电波传输干扰方面的认识。
