基于拉格朗日乘子法的冷水机组多目标运行优化

2021-08-29苗文筱张勇

建筑热能通风空调 2021年7期

苗文筱张勇

东南大学能源与环境学院

0 引言

随着我国公共建筑面积在总建筑面积中的比例升高，其能耗比例已上升到38%[1]，建筑节能迫在眉睫。利用优化方法，对冷水机组的负荷分配和运行策略进行优化，可以节省大量能源。

目前提出的优化方法有很多，根据最早致力于二次方程系统解决空调系统优化的Braun[2]的研究，对于同型号的两台冷水机，以相同的部分负荷率（PLR）运行的是其最佳调度。chang[3-4]通过拟合kW-PLR 曲线，将问题转化二次规划，采用拉格朗日方法求得最优解，并提出梯度法解决该缺陷。

随着机器学习的发展，越来越多的机器学习算法[5-6]也被应用到制冷领域。这些机器学习算法通过计算机强大的运算能力，寻找到最优解，可能会存在收敛过早，结果偏差，因此有许多改进算法方面的研究[7-8]。

由于二次规划对问题进行了简化，只选取PLR 为自变量，而冷水机组控制参数多，多目标优化可以更好地实现节能，因此本文提出一种基于拉格朗日多目标优化方法[9]，通过引入KKT 条件，对冷水机组多个运行参数进行优化，在满足总冷却负荷需求的条件下，实现最小化耗能。

1 系统结构

出于操作灵活性、维护便利的目的，空调系统经常使用多台冷水机组，并采用二次泵变流量系统实现一定程度的节能。二次泵变流量系统是一种分离式系统，在冷源侧提供恒定流量，从而防止温度过低未损害蒸发器并避免冷却器频繁停机。在负荷侧可以根据伏在变化通过二通阀调节流入末端的冷水流量，图1展示了一个多台冷水机组成的二次泵变流量系统[10]。

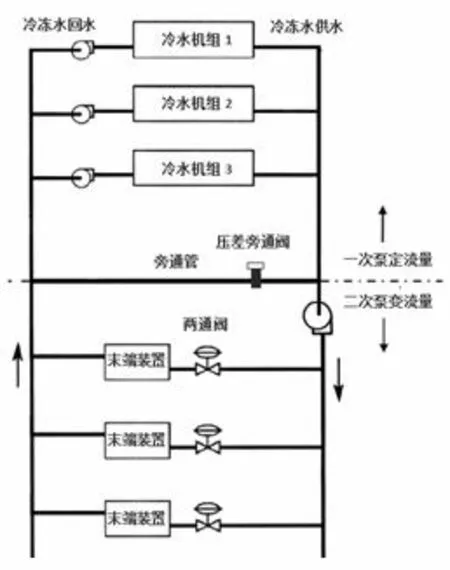
图1 多台冷水机的二次泵系统

冷水机组的制冷量可以通过以下公式计算：

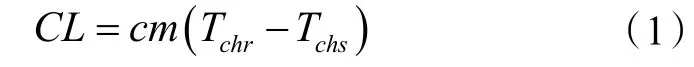
式中：m 表示冷冻水流量，kg/s；c 表示冷冻水的比热，J/(kg·K)；Tchr表示冷冻水回水温度，K；Tchs表示冷冻水供水温度，K。

冷水机组的制冷量可以通过测量冷冻水的流量，供回水温度来确定，各台冷水机表盘读取设定参数蒸发温度，冷凝温度，负荷率，通过功率计测量输入功率（kW），然后可以通过回归获得曲线。

2 拉格朗日函数构建

2.1 目标函数及约束条件

ASHRAE 在1999 年手册[11]提出了冷水机组运行优化的概念，其中通过拟合十次多项式对冷水机组进行能耗建模，选取冷却水回水温度Tcor,i，冷冻水供水温度Tchs,i和冷水机组负荷作为自变量，能耗可表示为：

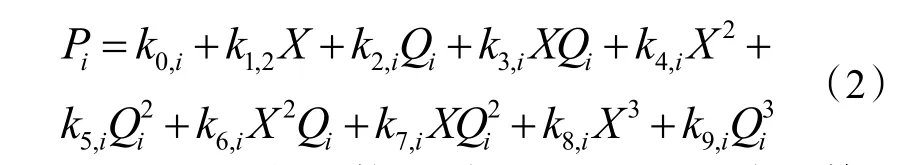
式中：k0,i～k9,i是回归系数；X 表示Tcor-Tchs；Qi表示第i台冷水机的制冷量。

本文提出一种同时改变冷冻水和冷却水温度的负荷优化分配方案，当满足负荷要求的同时冷水机组的总能耗降至最低时，即得出最佳的运行方案。同时制冷量与设计容量的比值为部分负荷率（PLR），因此式（2）可以改写为：

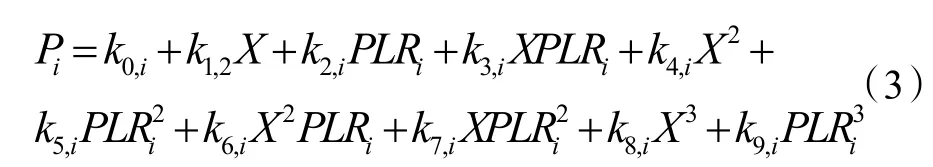
实际运算中，根据式（3）拟合得到的能耗模型与去掉三次方项拟合得到的线性方程精度相差无几，因此，去掉三次方后的简化模型为：

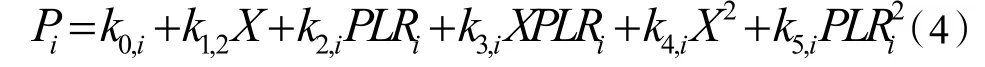
最佳冷水机组运行策略是找到一组冷水机组输出，该输出不违反运行极限，同时目标函数最小，目标函数为：

目标函数J 是每个冷水机组消耗功率的总和，其中m 是冷水机组的总数，Pi是第i 个冷水机组消耗的功率。同时必须满足平衡方程：

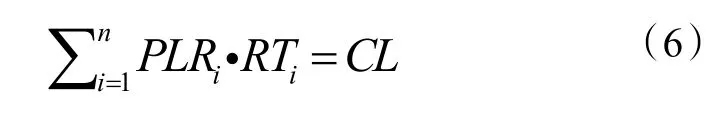
RTi是第i 个冷水机组的容量，CL 是所需的冷负荷，这是一个等式约束条件，除此之外还需满足不等式约束条件。冷水机组都有其设定的工作范围区间，超过该区间的解没有实际意义。无论什么类型的冷水机组，长期低负荷运行都容易发生故障，因此PLR 取33%以上，根据冷水机组出厂数据，大致划定温度范围，不等式条件如下：

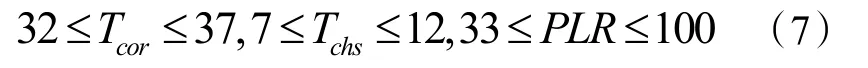
则：20≤Tcor-Tchs,i≤30

令Ti=Tcor,i-Tchs,i，表示在固定的冷却水温度下，不同的冷水机组的冷却水回水温度与冷冻水供水温度的温差。

将约束条件全部写成如下形式，构成4 个不等式组如下：

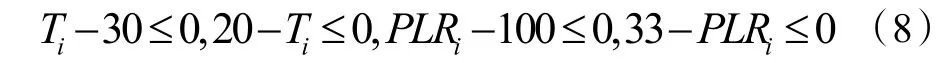
上述的约束条件对问题集合进行了定义，确保了该问题是一个凸集，并且是一个凸优化问题，避免了出现局部极小值的问题[12]。

2.2 拉格朗日函数

通过结合目标函数方程与约束条件，构造拉格朗日函数：

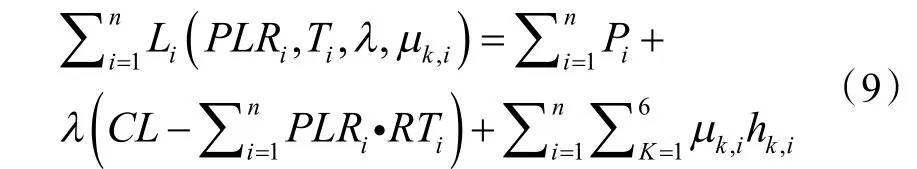
式中：λ，μk，i称作拉格朗日乘子。

对于同时存在等式约束和不等式约束的拉格朗日函数，极值存在的充分必要条件被称作KKT（Karush-Kuhn-Tucker）条件，如下：

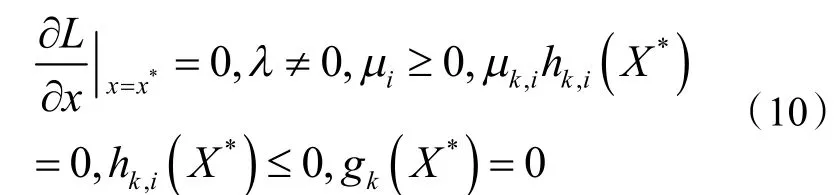
式中：X*为最优解（PLRi,Ti），gk(x)为等式约束，hk,i(x)为不等式约束。

在本问题中，根据KKT 条件，需要求解的方程组如下：

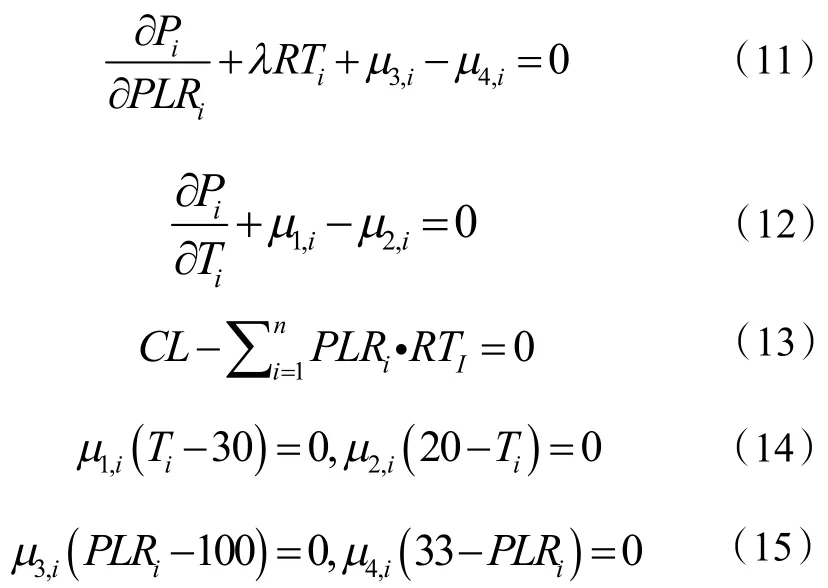
根据上边的方程求解所有未知数，代入KKT 的不等式条件，满足所有条件的解即为最优解。

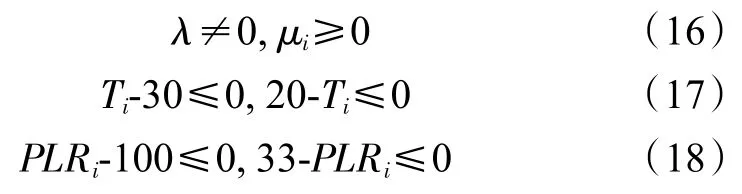
3 计算实例

3.1 目标函数

该方法对上海某医院空调系统数据进行了测试，该系统由两台磁悬浮冷水机组和两台螺杆冷水机组构成，采用二次泵变流量调节，系统运行时间较短，冷水机组损耗较少，因此同款冷水机组建立相同的能耗模型，上述能耗模型中i=2，因此待求解的优化参数共有四个，分别是磁悬浮冷水机组和螺杆冷水机组的部分负荷率以及冷却水回水温度与冷冻水供水温度的温差。首先将冷水机组运行数据分为5 份，4 份为训练数据，1 份为测试数据，通过sklearn 库自带的交叉验证模块对冷水机组能耗曲线进行拟合，并选取r2-score和均方误差（MSE）作为曲线准确度评价指标，表1 显示了十次多项式与简化后模型的得分对比。

由表1 可以看出来，两种能耗模型的得分相近，选择哪一个作为目标函数都在精度要求内，而十次多项式模型求导复杂，考虑之后计算简便，故选取简化后的模型，表2 中列出了简化模型下磁悬浮与螺杆冷水机组模型回归系数。为了更直观体现出模型的准确性，图2 显示了在该模型下，两台冷水机组预测值与实际值的偏差，直线上的点表示真实值与预测值完全相等。从图2 可以看到，简化后的模型对数据的有很好的预测精度。

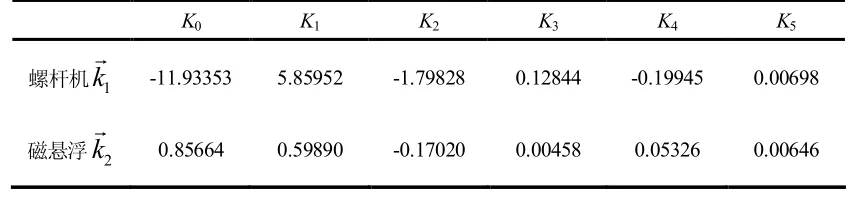
表2 磁悬浮与螺杆冷水机组模型的回归系数

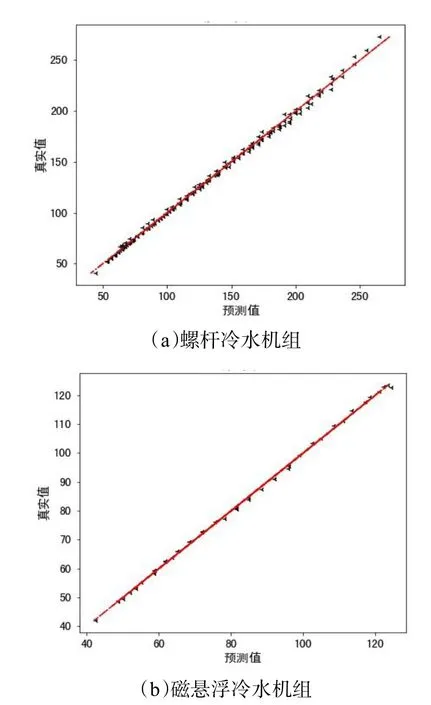
图2 简化模型预测结果与真实值对比

3.2 拉格朗日函数

在得到冷水机组的能耗模型后，根据式（5）～（9）构建拉格朗日函数。由于本系统中磁悬浮冷水机的出厂数据中，制冷百分比分母选择较小，因此存在了部分负荷率大于100 的情况，将磁悬浮冷水机的部分负荷率的最大值设置为采集到数据中的最大值，图3 显示了螺杆冷水机组在约束条件内的能耗范围，中间层为螺杆冷水机组能耗模型，上层为约束条件内的能耗平移所得，底层为约束条件。

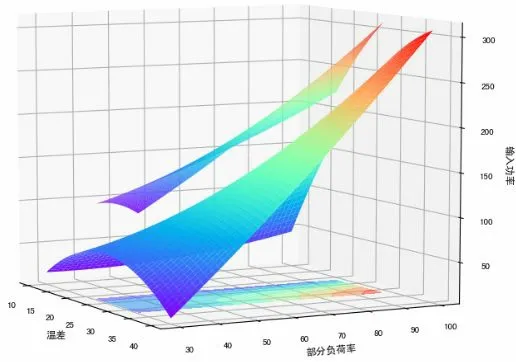
图3 螺杆冷水机组在约束条件内的能耗

本系统的拉格朗日函数如下：

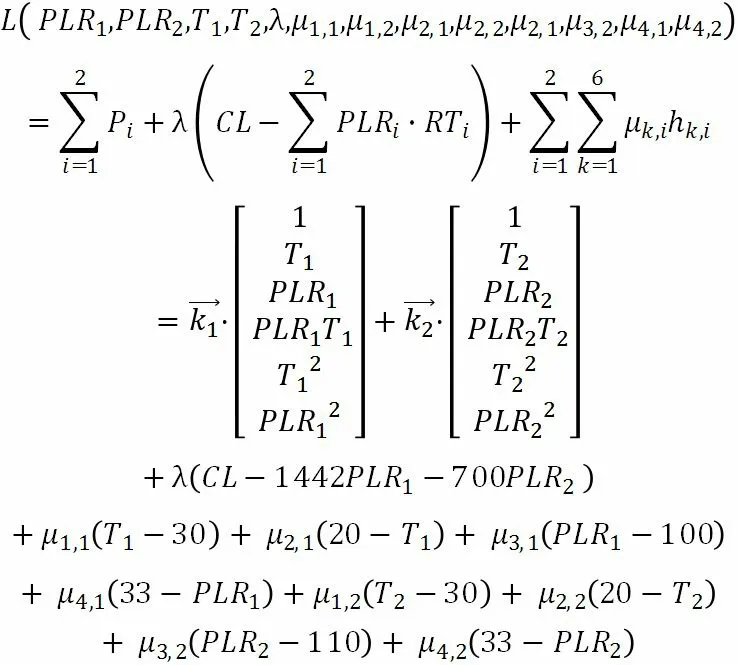
其中CL 为某刻冷负荷，可由式（1）获得。根据KKT 条件，得到13 个方程式，通过sympy 库中的solve 求解方程组，得到该问题不考虑约束下的所有解，选择了满足约束条件的解，即为该优化问题的最优解。

表3 列出了5 组实测冷水机组供回水温度与流量数据，用来计算冷负荷，由于不同机组温度传感器的误差，导致蒸发器进水温度有些许差异。其中1、2 号机器为螺杆冷水机组，3、4 表示磁悬浮冷水机组，每组工况中的数字表示实际运行中开启的机组。5 中测试工况的的运行方案由根据调试经验决定，为调试得到的最优运行工况。

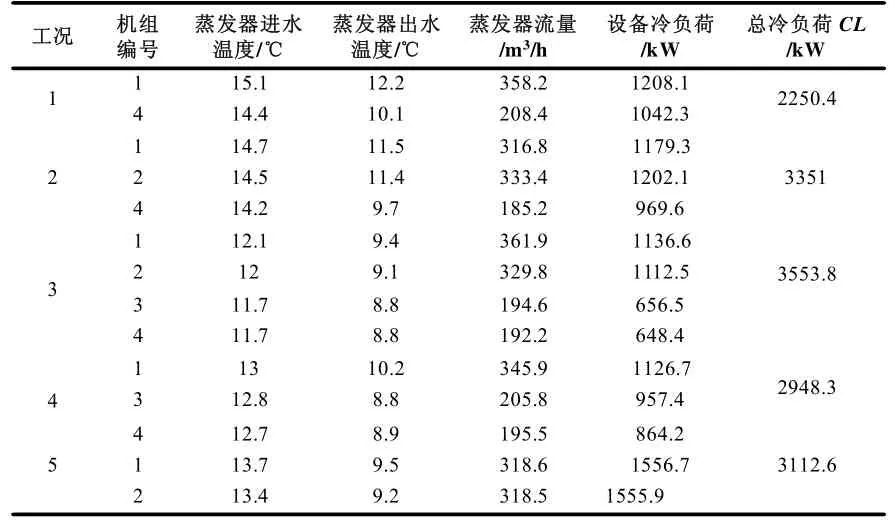
表3 实测运行数据

建立模型中，输入参数都是单台设备，对于相同部分负荷特性的冷水机组，平均分配为最佳分配，因此可以将相同冷水机组看成一台，将其对应的扩大相应的倍数即可求解。通过求解上节建立的拉格朗日函数，可以得到在各个工况的优化结果，表4 显示了调试方案、最佳优化方案与考虑温差的实际优化方案对比。

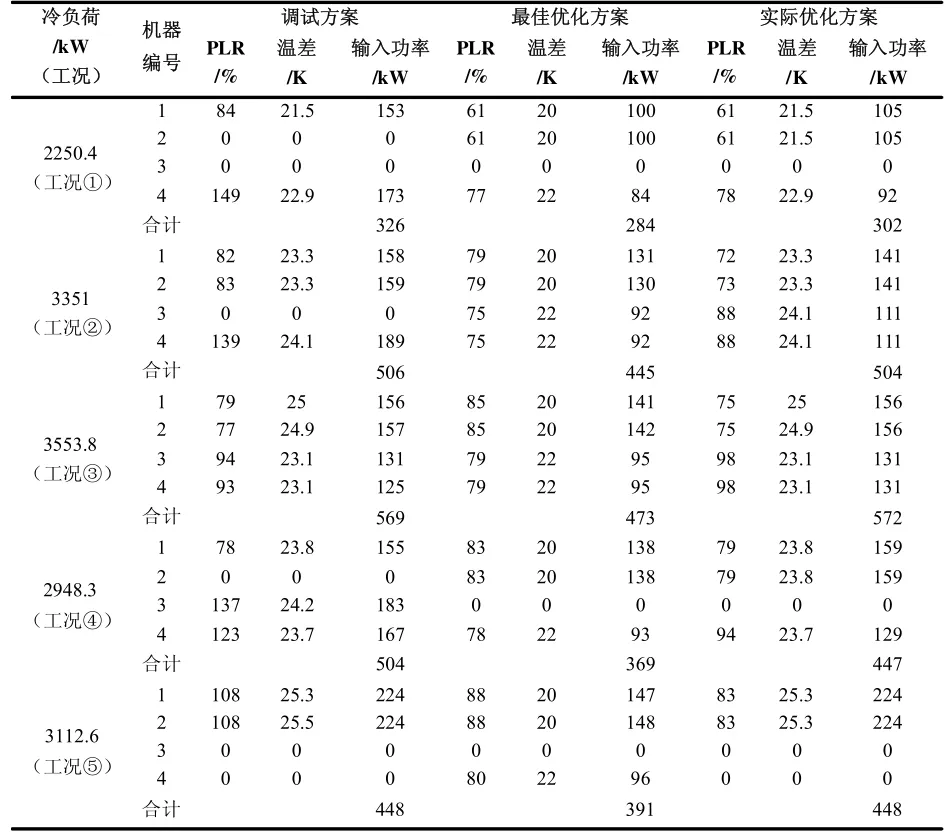
表4 优化结果

由表4 可以看到，对比调试方案，拉格朗日优化后的运行方案都实现降低输入功率的目标，在20 K 温差下，五种工况的平均节省了16%的功率。

由表4 可以看到，对比调试方案，拉格朗日优化后的运行方案都实现降低输入功率的目标，在20 K 温差下，五种工况的平均节省了16%的功率。在一个卡诺循环中，耗功与高低温热源温差成正比，因此越低的温差，系统耗能越少。减少温差可以从两方个面：一是降低冷却水供水温度，考虑到环境湿球温度的改变，根据冷却塔运行能力，尽可能降低的冷却水供水温度，从而减少冷却水回水与冷冻水供水温差。二是在一定范围内合理的提高冷冻水温度，在本文测试的工况中，蒸发器出水在8.8～12.2 ℃之间，有效地降低了冷却水回水与冷冻水供水温差。

表5 列出了不同工况对应的环境湿球温度，考虑到冷却水回水与湿球温度Ts冷却能力有关，温差不能盲目取最小。为显示本研究的优化效果，与调试方案采取相同温差在，对比各工况的耗功。可以发现，根据经验的运行方案大部分时间与计算得到的优化运行方案相匹配，这时的螺杆冷水机组的部分负荷率在80%左右，在开启3 台冷水机组的工况中，开启2 台螺杆冷水机组较开启2 台磁悬浮冷水机组更为节能。这与设备出厂数据不符，经过排查，发现了磁悬浮冷水机组冷凝器有堵塞，冷却水回水温度过高，输入功率增加。