基于蒙特卡罗算法的列车网络控制系统可靠性仿真分析

赵 强

(中车长春轨道客车股份有限公司，吉林 长春 130062)

列车网络控制系统(TCMS)是动车组、城市轨道车辆的重要系统之一，对全车的关键设备进行控制、监视、故障诊断，其可靠性是保证车辆安全运行的决定性因素。作为涵盖固有化硬件(如中央控制单元、网关、显示器、中继器及输入输出模块等)及关键性软件(如系统软件、应用软件、调试测试软件及PC机工具软件等)的复杂网络信息传输系统，其系统故障可能是由于任何软件、硬件或传输介质故障所造成的，因此其可靠性分析应综合考虑所有软件和硬件故障模式的影响，通过一个统一的数学模型进行综合计算。

蒙特卡罗算法以概率论及数理统计为理论基础，利用重复的抽样、统计试验直接或间接针对数学模型进行大量统计模拟试验，用以有效解决很多用传统数理统计或物理试验难以处理的问题[1]。本文以北京地铁6号线列车网络控制系统为例，在说明其系统组成、规定条件及任务的基础上，建立了系统可靠性综合模型，说明了应用VB语言开发TCMS可靠性数字仿真程序的使用方法，采用蒙特卡罗仿真法计算了TCMS的可靠性指标，对于进行复杂网络系统(涵盖硬件、软件及网络通信)的可靠性预计分析具有借鉴意义。

1 TCMS规定条件和任务要求

北京地铁6号线TCMS的设计符合IEC 61375-1：1999《铁路电气设备列车总线国际标准》的要求，TCMS主要通过中央控制单元(CCU)与各子系统的控制单元间的信息传输实现对车辆子系统设备的控制、监视及故障诊断功能。图1为北京地铁6号线列车网络拓扑图，该图说明了TCMS系统与各子系统控制单元之间的信息传输关系。

ERM.列车数据记录仪；RIOM.远程输入/输出模块；HMI.人机接口单元；BCU.制动控制单元；PA.列车广播系统；FAS.烟火报警系统； ATC.列车自动控制系统；HUB.集线器；RPT.中继器；HVAC.空调系统；TCU.牵引控制单元；DCU.门控单元； ACU.辅助控制单元；MC.主控器；EMD.电气中距离。

从可靠性冗余设计角度考虑，在列车网络控制系统中，CCU是主要的控制部件，其主要功能是完成底层MVB通信数据的收发和控制逻辑的运算[2]。因此，TCMS设有2个CCU，这2个CCU在运行中互为热备份，如果主CCU故障，另一个CCU会接替主CCU进行工作。RPT和RIOM都采用冗余的技术方案，任何一个单点故障都不会影响列车的正常运行。HMI用于在施加列车运行控制指令的同时进行各子系统故障状态信息的显示，显示屏通过MVB总线、以太网总线与CCU接口，对于实时性要求高的控制指令、状态数据通过MVB总线进行传输，其他数据通过以太网总线进行传输，可有效减轻网络负载率。为防止车辆在运行过程中因车间线缆断裂引起列车网络故障，在车间增加了车间分线器，提高了车辆运行的安全可靠性。

TCMS可靠性任务要求由地铁运营商与TCMS供应商在设计阶段进行确认，并在车辆交付后进行验证。对TCMS故障按照其对列车营运的影响进行分类及定义，即在列车正常运行期间，对由于TCMS故障直接或间接导致的列车故障(包括运营服务故障、晚点故障及维护故障)进行分类及定义。北京地铁6号线TCMS可靠性的任务要求是服务故障平均无故障时间为48 400 h，晚点故障和维护故障时间分别为22 400 h和1 000 h。

2 TCMS的可靠性综合模型

TCMS的可靠性综合模型是综合考虑系统的软硬件故障给出的系统可靠性模型，体现为系统构件层和拓扑层可靠性模型的融合。建模过程中考虑到融合的复杂程度，采用将软件拓扑可靠性模型融入到硬件拓扑可靠性模型中的方式，即在硬件的故障树模型中加入软件的故障。硬件拓扑可靠性模型根据底层设备的失效分布抽取故障时间；而在软件拓扑模型中，构件的故障判据根据概率抽样得出首次故障时软件模块执行周期数的正态分布参数，然后根据软件模块的执行周期转化为软件模块首次故障的时间，最后综合软件与硬件的故障时间进行故障树的蒙特卡罗仿真，给出TCMS整体的可靠性指标值。

复杂系统可靠性分析应符合其自身的特点，越复杂的系统和结构越会导致多种失效模式共存，多种失效模式之间相互作用、彼此影响，往往存在竞争失效问题[3]。TCMS软件和硬件的故障模式多样，单纯建立系统常规的可靠性框图，仅应用串联、并联等逻辑关系难以全部包容软件和硬件故障模式的影响，因此考虑从功能结构角度进行故障模式影响分析(FMEA)。FMEA分析过程中，由于受系统软件应用开放性限制，除CCU以外的软件系统(如HMI,RIOM)在建模过程中均作为黑盒处理，而对于TCMS重要设备RIOM的软件故障在明确其软件构成的前提下，可以采用与CCU同样的方式进行软件故障建模分析，最终通过FMEA找出所有软件和硬件故障模式对TCMS功能的直接影响。利用故障树的逻辑关系(包括时序关系的影响)建立TCMS可靠性综合模型，如图2所示。

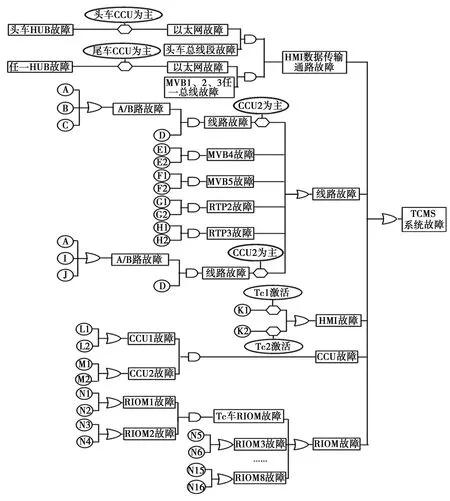
A.MVB2 A/B路故障；B.MVB1 A/B路故障；C.RPT1 A/B路故障；D.任意A/B路故障；E1.MVB4 A路故障；E2.MVB4 B路故障；F1.MVB5 A路故障；F2.MVB5 B路故障；G1.RPT2 A路故障；G2.RPT2 B路故障；H1.RPT3 A路故障；H2.RPT3 B路故障；I.MVB3 A/B路故障；J.RPT4 A/B路故障；K1.HMI1故障；K2.HMI2故障；L1.CCU1软件故障；L2.CCU1硬件故障；M1.CCU2软件故障；M2.CCU2硬件故障；N1.RIOM1硬件故障；N2.RIOM1软件故障；>N3.RIOM2硬件故障；N4.RIOM2软件故障；N15.RIOM8硬件故障；N16.RIOM8软件故障。

3 TCMS可靠性蒙特卡罗仿真

3.1 仿真逻辑设计

常规的故障树定量计算中，无法对逻辑时序关系、非指数分布情况及维修情况等进行解析计算[4]，因此本项目采用蒙特卡罗方法对上述故障树逻辑模型进行仿真分析和计算。根据蒙特卡罗仿真思想，TCMS可靠性仿真的逻辑设计图如图3所示。TCMS系统可靠性数字仿真采用离散事件驱动的模拟方法，仿真核心是对一个事件队列的处理，该队列按照事件发生的时间先后进行排序，每一个事件将会产生一个中断等待处理，随着仿真时钟推进，设备故障及设备维修等不同事件会进入队列中驱动仿真推进。

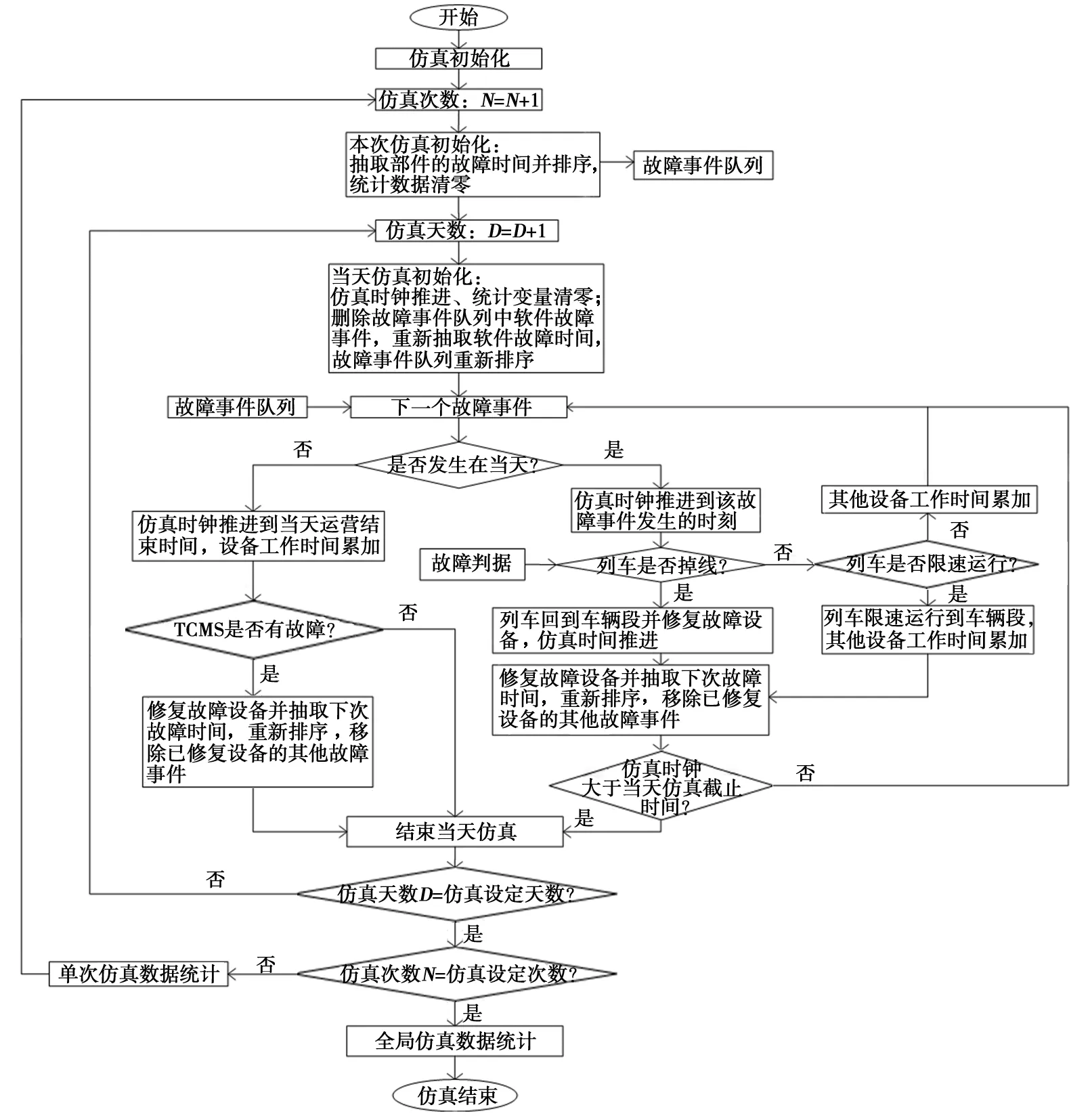
图3 TCMS可靠性仿真逻辑设计图

3.2 数字仿真程序

为实现对上述模型的计算，项目采用VB语言开发了一个可靠性数字仿真程序，其界面设计如图4所示,该程序对应蒙特卡罗可靠性仿真的逻辑，在故障树的基础上同时考虑了部件的维修问题。通过仿真软件在TCMS可靠性模型上建立节点设备及节点间的连线物理连接关系，完成TCMS的拓扑结构，对TCMS组成单元的属性进行设置，包括设备信息、可靠性参数和维修性参数，也包括TCMS相应单元中的软件模块的可靠性参数。

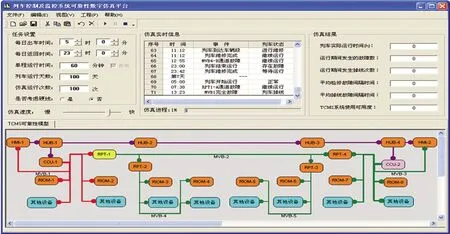
图4 TCMS可靠性数字仿真程序

在仿真过程中各种事件可以实时显示，故障设备的状态同时会在TCMS拓扑图中显示出来，对于丧失功能的设备用红色标示，对于只有1个通道故障时用黄色标示，主CCU故障以粉色标示；仿真结果显示框显示的数据是本次仿真的结果，多次仿真结束后，仿真结果显示框中显示的信息是多次仿真的平均值。

TCMS可靠性数字仿真程序采用离散事件驱动的模拟机理(“事件”是指TCMS状态的变化)，仿真过程中仿真核心维护着1个故障事件队列，该队列按照事件发生的时间先后进行排序，队列的第1个事件将产生1个中断，处理完该故障事件后该事件被删除，随着仿真时钟的推进，不断有设备故障，故障设备维修后又会有新的故障事件插入到故障事件队列中形成仿真推进的动力，当满足退出条件时则仿真终止[5]。

3.3 仿真分析计算

数字仿真程序应用的输出结果包括列车的平均运行时间、运行期间发生的平均故障次数、发生的平均掉线故障次数、平均检修故障间隔时间、平均掉线故障间隔时间和TCMS系统使用可用度，之后的应用中可以根据需求统计其他需要的可靠性、维修性和可信性等参数。

列车的平均运行时间TOP是多次TCMS仿真中列车运行时间的平均值，列车运行期间发生的平均故障次数FN是多次TCMS仿真中列车发生的所有故障次数之和的平均值，发生的平均掉线故障次数CFN是多次TCMS仿真中列车发生的所有掉线故障次数之和的平均值。

单次TCMS仿真和多次TCMS仿真后的平均检修故障间隔时间分别为MTBFi和MTBF，计算公式为：

(1)

(2)

式中：TOPi——每次TCMS仿真时的列车运行时间；

N——仿真次数。

单次TCMS仿真和多次TCMS仿真后的平均掉线故障间隔时间分别为MTBCFi和MTBCF，计算公式为:

(3)

(4)

系统的使用可用度Ao是指系统当需要时能够正常工作的程度，其计算公式为:

(5)

式中：TT——TCMS的任务时间；

DT——TCMS不能工作的时间。

3.4 仿真数据输入

仿真数据输入包括对列车运行任务剖面数据的设置以及TCMS组成单元参数的设置。

3.4.1 仿真任务设置

假设列车的任务时间为6年，每月有1天的时间需对列车进行检查，检查当天列车不运行，每年按365天计算，则6年内列车总的任务时间为(365-12)×6=2 118(天)，其余任务参数设置如下：每日出车时间为5:00 a.m.，每日返回时间为11:00 p.m.，单程运行时间为90 min，仿真运行次数为20次。

3.4.2 设备参数设置

依据可靠性理论和大量工程实践，复杂系统故障规律一般服从指数分布[6]。列车各系统及其子系统均属于复杂系统，且在正常运行期间的故障率是基本恒定的，其基本部件的故障规律基本服从指数分布。考虑到项目设计阶段无法确定TCMS组成单元的可靠性和维修性参数，硬件的可靠性参数按照可靠性分配的结果取值，软件的可靠性和设备的维修性参数则初步给一个参考值，软件可靠度和维修时间分布参数分别设为0.99和1 h计算分析中采用的设定仿真输入数据如表1所示。

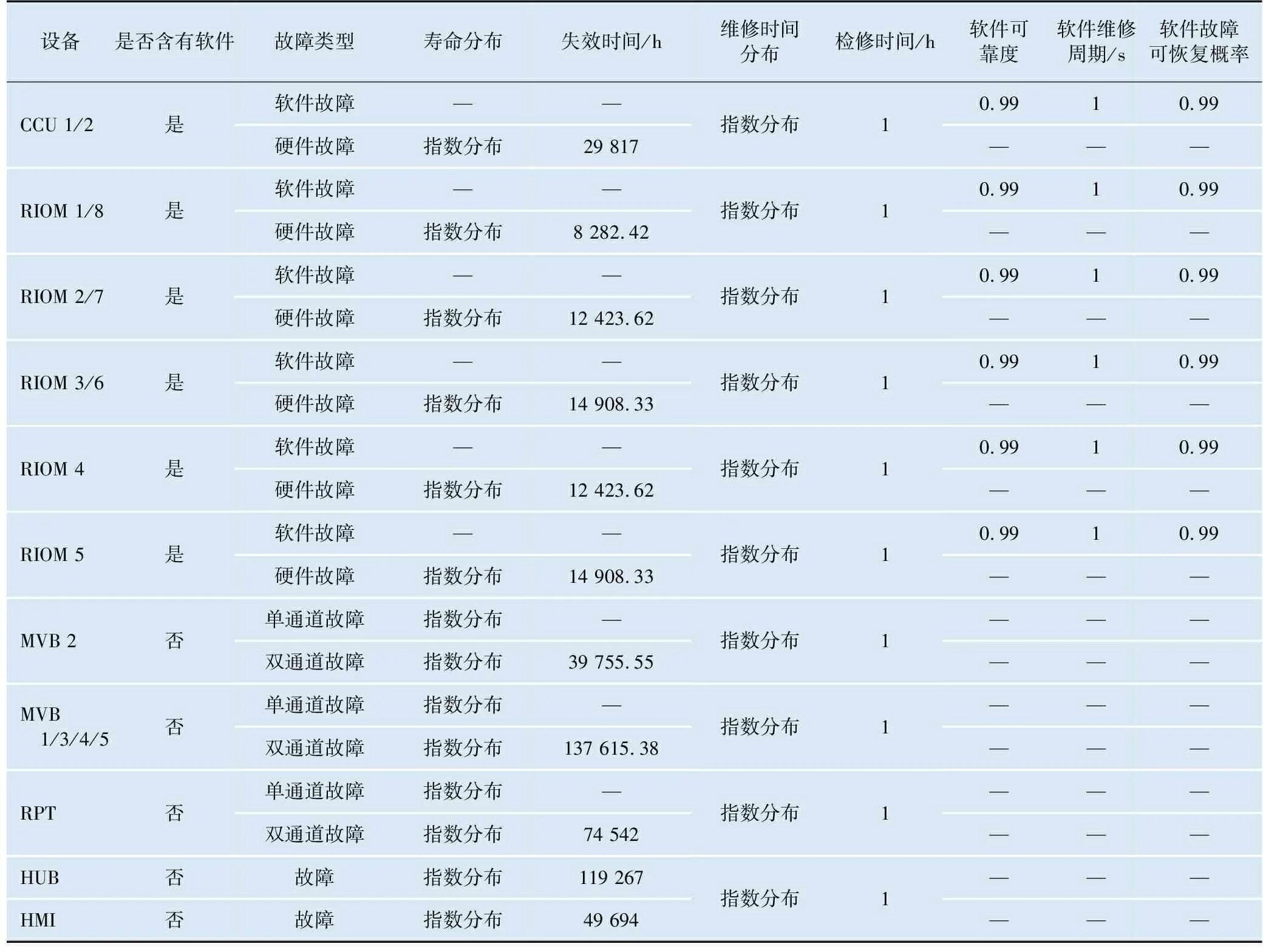
表1 仿真输入数据设置

3.5 仿真运行及结果分析

在数字仿真程序开发完成的基础上，对TCMS的硬件组成可靠性以及TCMS软硬件综合的可靠性水平进行仿真分析，仿真运行在假设条件下进行，获得更详细车辆实际运营数据后进行仿真时仿真结果会更加准确。

3.5.1 TCMS硬件可靠性仿真结果

将含有软件单元的软件可靠度数值设为1，即认为软件不发生故障，其他参数按表1中所列数值进行设置。TCMS硬件组成可靠性仿真结果如表2所示。

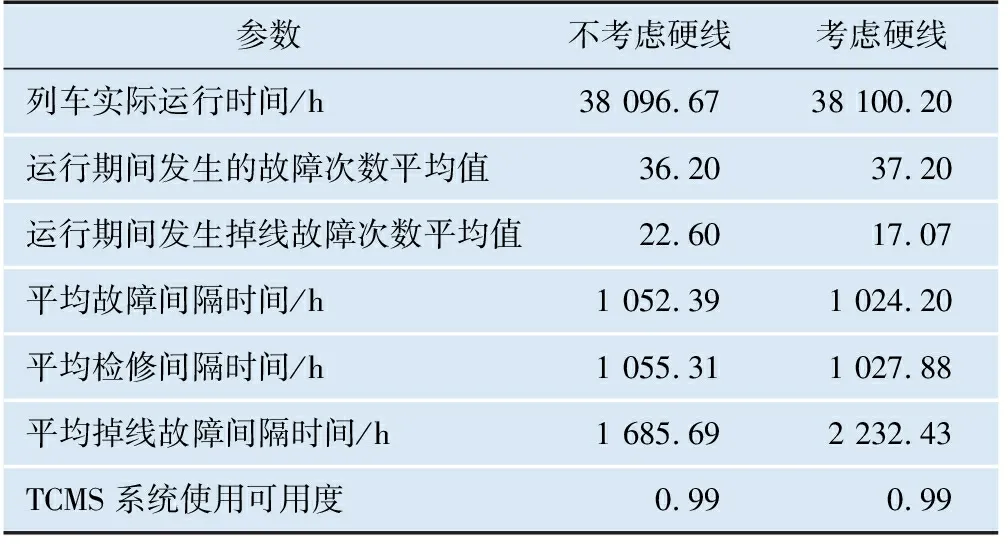
表2 TCMS硬件组成可靠性仿真结果

3.5.2 TCMS软硬件综合可靠性仿真结果

在TCMS可靠性数字仿真程序中输入表1中参数，在综合考虑软硬件故障的情况下，TCMS软硬件综合可靠性仿真结果如表3所示。

表3 TCMS软硬件综合可靠性仿真结果

3.5.3 仿真结果对比分析

将TCMS硬件组成可靠性仿真结果及软硬件综合可靠性仿真结果进行对比分析，可以得到以下结论：

(1) 不考虑软件故障的情况下，列车运行2 118天平均发生的故障次数为36.2次(不考虑硬线)和37.2次(考虑硬线)。TCMS硬件的平均故障间隔时间为1 052.39 h(不考虑硬线)和1 024.20 h(考虑硬线)，与可靠性分配的指标(1 000 h)基本相符。

对于TCMS的硬件组成，考虑硬线备份后，列车运行2 118天平均发生的掉线次数由22.6次降为17.07次，列车的平均掉线故障间隔时间由1 685.69 h提高到2 232.43 h，提高了32.43%。

(2) 综合考虑软件和硬件故障，列车运行2 118天平均发生的故障次数为1 440次左右，通过与硬件组成的仿真结果进行对比可知，其中软件故障有1 400次左右。TCMS的平均故障间隔时间为26.4 h 左右，由于软件故障后可恢复的特性，由TCMS故障导致的列车掉线次数较少，但是比硬件组成多9次左右。

(3) 综合考虑软件和硬件故障，在加入硬线备份后，TCMS的平均掉线故障间隔时间由1 220.58 h 提高到1 426.52 h，提高了近16.87%。由于硬线只是对MVB网络(MVB总线、中继器、分线器)连通性的备份，对软件故障没有备份功能，硬线备份后TCMS的平均掉线故障间隔时间的提高主要是硬线设计对网络连通可靠性的提升。

4 结束语

国产化列车网络控制系统开发及应用对硬件、软件及系统集成可靠性指标要求不断提高，产品开发过程中如何针对具有硬件、软件、网络通信的复杂系统进行可靠性指标预计并进行工程化应用一直是车辆系统集成需要面对和解决的问题。本文以列车网络控制系统这一复杂网络系统为分析对象，建立了基于蒙特卡罗算法的可靠性仿真预计分析模型，应用开发的数字仿真程序进行了仿真预计分析，根据仿真分析结果协调设计参数进行方案比较，以发现系统设计的薄弱环节，对复杂网络系统的可靠性及维修性设计工程化具有一定的借鉴意义。