以教材习题为生长点，拓展学生思维空间

汪建华

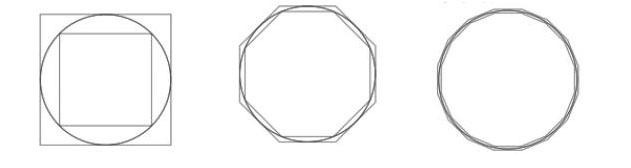
一、教材的原题

看一看，比一比，你发现了什么？

圆的面积比圆外的正方形面积小，比圆内的正方形面积大。

三、教学片段与思考

（一）联系生活，情景导入。师：在奇妙的数学王国里，圆形与正方形的关系非常密切，在中国建筑中经常能见到外方内圆和外圆内方的设计（出示图），今天这节课我们就来研究圆与正方形之间的关系。（设计意图：从生活中熟悉的图形抽象出圆与外切正方形、内接正方形的例子，明确本课学习的内容。直截了当，让学生体验生活处处有数学，数学来源于生活）

（二）探索研究，理解掌握

1.研究外方内圆

环节一：（出示四道练习题，让学生完成）

（1）正方形的边长为4cm，求圆的面积是多少平方厘米？

（2）正方形的面积为36cm2，求圆的面积是多少平方厘米？

（3）正方形的面积为60cm2，求圆的面积是多少平方厘米？

环节二：（学生完成后提供学习纸，让学生探究圆与正方形的面积关系，把发现写下来）

把刚才3题的数据填在表上，比较圆的面积和正方形的面积，你有什么发现吗？

（设计意图：这个环节三道题由易到难，层层深入，让学生明白，求圆的面积，除了知道圆的半径、直径、周长以外，如果知道圆的外切正方形，一样能求这个圆的面积。圆的面积=外切正方形的面积÷4×π。另外从浅层次的三道题，当学生把每题的圆的面积与正方形的面积一对比，不难发现：尽管三道题都不同，但是圆的面积÷外切正方形的面积=0.785，说明圆的面积与其外切正方形的面积的比例是与圆的大小无关）

环节三：探究圆的面积÷外切正方形的面积=0.785的本质。

如果圆的半径是r，圆的面积=

，正方形面积=               ，圆的面积÷正方形的面积=       。（设计意图：本环节给学生提供一定的思路，让学生带着问题有方向地思考、探究。通过探究发现：圆的面积=πr2，正方形的面积=2r×2r=4r2，所以圆的面积÷正方形的面积=πr÷4r=π/4=0.785，从而发现两个图形的商是和半径无关的，也就是圆的大小无关。而且商是一个定值0.785。从而让学生清楚圆的面积=外切正方形的面积×0.785这一数学规律）

环节四：针对练习

四张边长都是12cm的正方形铁皮，分别按照下图剪下不同规格的圆片，哪张铁皮剩下的废料多？（设计意图：有针对性的练习能够加深学生的印象，巩固所发现的规律，同时让学生体验圆的面积=外切正方形的面积×0.785这一规律的简易、快捷）

四、教后体会与反思

（一）在数形结合中悟方法。我们都知道圆的面积公式为S=πr2，运用面积公式求圆的面积，关键是先求圆的半径。然而，我们经常会遇到一些题目，不能直接求出圆的半径，但如果能巧妙灵活地利用r2，问题也会迎刃而解。

（二）在比较分析中找关系。圆与正方形之间的大小关系通过观察得到，但不能准确地刻画。因此，要借助研究数据，在比较分析中发现它们之间的关系。例如，教师以表格的形式出示学生的研究数据，然后经过比较分析，学生发现了圆的面积与外切正方形的面积之间的比值是0.785，即圆的面积是它的外切正方形面积的78.5%。当学生研究圆的面积与内接正方形的面积时，再次引导学生比较分析，从而发现了圆的面积与它的内接正方形的面积之间的比是157：100。最后对圆的面积與它的外切、内接正方形的面积这三者再次进行比较分析，发现了它们之间的关系是：4r2>3.14r2>2r2。

（三）在多种策略中提技巧。有关圆与正方形的面积知识灵活多变，而且解题策略有多种。如其中的练习题求哪张铁皮剩下的废料多，我们可以根据提供的条件分别求出正方形的面积与所有圆的面积，相减后再比较大小，也可以先求出圆的面积或正方形的面积，再根据它们之间的关系求另一个图形的面积，相减再比较，还可以先求出正方形的面积，再根据它的内切圆形的面积是的0.785得到圆形的面积，相减后比较大小，可以用不同的方法解题。

责任编辑    徐国坚