回归分析法在水源地扩大开采中的应用研究
2021-08-27杜红磊刘双才
杜红磊,刘双才
(河南省地质矿产勘查开发局第五地质勘查院,河南 郑州 450001)
地下水资源量与许多因素有关,比如地下水水位埋深、大气降水量、蒸发量、开采区的面积等,若将这些因素作为自变量,则它们与地下水资源之间存在着统计相关关系。回归分析法是利用长序列、系统的数据观测资料,用数理统计法找出一个水源地中地下水开采量与地下水水位之间的相关关系,通过建立回归方程外推水源地地下水在设计降深的情况下的可开采量。本文利用周范水源地多年系统的开采量、水位观测资料,建立回归方程,并利用方程对水源地外推设计降深时的开采量进行预测或在设定水源地开采量的情况下预测地下水水位的变化。
1 水源地概况
周范水源地位于西平县城西部,位于洪河冲积平原上,地表岩性主要为褐黄色粉质粘土。水源地现已运行多年,主要向西平城区供水,设计取水规模2.0万 m3/d。县域多年平均降水量为856 mm、蒸发量为1 478 mm。洪河属淮河水系是区内主要常年性河流。区内河流属于淮河水系,其中洪河为主要常年性流水河流,多年平均流量8.35 m3/s。中深层地下水含水层是水源地主要开采层位,含水层顶板埋深50~70 m,底板埋深250~300 m;含水层岩性主要为第四系冰湖相(Q1lgl)沉积层中粉细砂、中粗细砂及含砾中粗砂。根据抽水试验数据,充分考虑含水层厚度,同时结合钻孔单位涌水量的大小,将研究区中深层地下水富水性统一按300 mm口径,统一降深15 m时,根据单井涌水量划分为强富水区(单井涌水量为3 000~5 000 m3/d)和富水区(单井涌水量在为1 000~3 000 m3/d)。
1.1 水源地地下水的补给、径流及排泄条件
补给:水源地开采层位地下水顶板埋藏深度较大,且上覆分布有连续、厚度大的粘土层,隔断了与上覆含水层的水力联系,因此径流补给是中深层地下水的主要补给来源。
径流:天然条件下,区内中深层地下水流向由西向东径流,径流缓慢;现状条件下,由于水源地大规模开采地下水致使在原周范水源地形成一个较大的降落漏斗,径流方向改为由四周向漏斗中心径流,水力坡度变大。
排泄:受水源地大规模开采地下水的影响,现状中深层地下水排泄方式由原来的径流排泄改变为人工开采。
1.2 水源地地下水的动态特征
天然条件下,中深层地下水受气象和水文因素影响较小,其动态比较稳定,水位上升比降雨稍滞后。地下水的动态变化主要受人为因素的制约,开采层位地下水水位随开采强度的变化而发生变化,其动态变化类型为径流—开采型。开采层位地下水动态变化主要受水源地开采量的影响,水位变化和开采量基本保持一致,年际水位最大变幅1.15~2.20 m。水位标高和开采量过程曲线见图1。

图1 水源地地下水水位和开采量关系曲线
1.3 水源地运行现状
周范水源地现已运行多年,拥有系统的的观测资料(见表1)。根据水位和水量观测资料分析可知:水源地地下水水位现在趋于稳定,没有明显下降趋势,处于相对平衡状态,水源地扩大开采后仍有补给保障(现在水位埋深24.96 m,含水层顶板埋深60.00 m)。

表1 水源地开采量和水位变化统计表
2 回归分析法预测可开采量
2.1 水源地含水层概化
不考虑水源地含水层的内部结构及水流状态,将含水层其视为一“黑箱”体,利用地下水动态长期观测数据,研究水源地开采量和水位降深的相互关系,建立两者之间的相关方程,从而达到利用方程预测可开采量或水位变化的目的。为此,从统计理论的角度,对含水系统进一步概化为:
(1)水源地开采层位的补给来源为主要为周边含水层的径流补给,不考虑越流,因此,系统为单一的输入;
(2)区内除了水源地开采地下水,其他机井开采量甚小,因此将系统内地下水的排泄概化为单一的输出;
(3)含水层面积大且分布连续,具有较强的调蓄能力,地下水动态较稳定,水位年际变幅较小,处于相对平衡状态,含水层特征函数不随时间变化。
由此将含水层概化为:含水层(X)、径流补给(Y)和开采(Y)构成单一输入、单一输出的线性水文地质系统(如图2所示)。

图2 周范水源地水文地质系统模型框图
2.2 回归模型
根据水源地长观资料中的开采量与水位降深资料绘制相关图(如图3所示)。根据开采量与水位降深的散点图可知,因变量开采量随自变量水位降深的增大而增大,而且散布点的分布在图上表现为一条近似直线。由此可以判断开采量与水位降深这两个变量之间存在着某种线性相关关系。对于具有某种线性关系的开采量和水位降深,现用一个线性回归方程来表示他们之间的线性关系,其一元线性方程回归模型为:
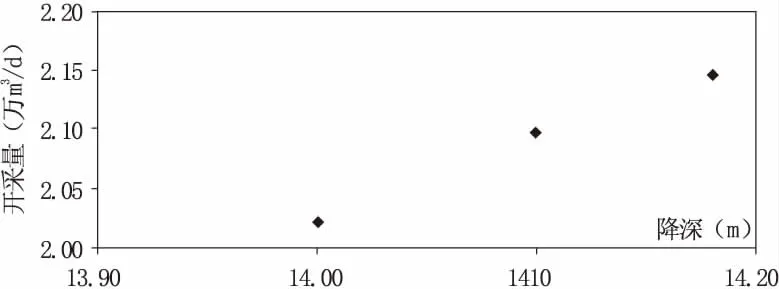
图3 周范水源地开采量和水位降深值相关关系图
Y=a0X+a1+ε
在这个回归关系模型中,开采量(Y)是一个线性函数,由水位降深(X)(a0X+a1部分)再加上误差项ε。
2.3 回归方程的计算及判断
本次分别选择直线回归方程和曲线回归方程进行比较计算,其中直线方程为Y=a0X+a1,曲线方程为lgY=a0lgX+a1。
2.3.1 直线回归方程
1)方程求取
利用最小二乘法求取回归方程参数值,通过计算确定直线回归方程为:
Y=0.695 428 X-7.712 82
(1)
式中:Y为开采量(万m3/d);X为水位降深(m)
2)显著性检验
本次直线回归方程的显著性检验包括线性检验和回归性检验。具体如下:
线性检验:在显著水平(α)为0.05、分子自由度为1、分母自由度为1的条件下,在相应F值分布表中查到相应的临界值Fα=161.448。由于F=297.21> Fα,说明两者之间的线性关系是显著的。

3)模型检验
根据数据分析绘制开采量与水位降深回归分析残差图(如图4)。根据残差图可知,图中所有点都落在-0.005~+0.005之间,说明开采量和水位降深之间关系的回归模型是合理的。

图4 水源地开采量与水位降深值回归分析残差图
综上分析,水源地开采量和水位降深二者的线性回归关系见图5,回归方程见表2,通过检验的回归方程可以用来预报水源地的开采量或预测水位降深。

图5 水源地开采量和水位降深关系图

表2 开采量和水位降深相关分析成果表
2.3.2 曲线回归方程
1)方程求取
利用最小二乘法求取回归方程参数值,通过计算确定直线回归方程为:
lgY=4.706 4lgX-5.088 1
(2)
式中:Y为开采量(万m3/d);X为水位降深(m)
2)显著性检验
回归方程的显著性检验包括线性检验和回归性检验。具体如下:
线性检验:在显著水平(α)为0.05、分子自由度为1、分母自由度为1的条件下,查得相应的临界值Fα=161.448。由于F=297.21>Fα,说明两者之间的线性关系是显著的。

3)模型检验
绘制水源地开采量与水位降深回归分析残差图(如图6)。根据残差图可知,图中所有点都落在-0.001~+0.001之间,说明开采量和水位降深之间关系的回归模型是合理的。

图6 水源地开采量与水位降深值回归分析残差图
综上分析,水源地开采量和水位降深二者的线性回归关系见图7,回归方程见表3,经过检验回归方程可以用来预报地下水的开采量或预测水位降深。
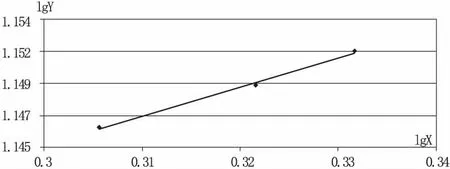
图7 水源地开采量和水位降深对数关系图

表3 开采量和水位降深相关分析成果表
2.4 利用回归方程外推预报
根据建立的直线回归方程和曲线回归方程分别外推计算在设计降深20 m时的水源地可开采量,计算结果见表4。根据两个方程的计算结果对比分析可知:直线回归方程可开采量预测结果更接近实际开采量。

表4 开采量预测结果表
3 结语
根据周范水源地多年观测资料分析可知,水源地年开采量与年水位降深两者之间存在着明显的线性相关关系。本文建立了水源地开采量与含水层水位降深的回归模型,利用最小二乘法求取回归方程的参数,建立回归方程。
(1)经过显著性检验和模型检验,回归方程均满足要求,利用方程预测水源地地下水的开采量,其中利用直线回归方程预测在设计降深下的开采量其结果更接近实际,证明建立的模型能够真实的反应水源地内部的水文地质特征。利用用在该模型基础上建立的回归方程预测周范水源地在设计降深时的开采量具精度较高。
(2)利用建立的回归分析预测周范水源地的开采量。认为水源地在扩大开采量(3.0万 m3/d)后其资源量是有补给保证的。预测未来扩大开采量后,水源地水位降深在允许范围内,稳定动水位仍处于承压含水层顶板以上,不会引发水源地地面沉降、水源枯竭等地质环境问题。该项研究对补给有余的水源地扩大开采量设计将具有重要的参考价值。
