揭露两个含水层混合井初始混合水位形成机理研究
2021-08-27李超峰姬亚东
李超峰,姬亚东
(1.中煤科工集团西安研究院有限公司,陕西 西安 710077;2.陕西省煤矿水害防治技术重点实验室,陕西 西安 710077)
地下水混合井流问题是实际工作中普遍存在的[1-2]。关于混合井的定义,郭东屏主编的《地下水动力学》[2]将其定义为“能同时汲取两类含水层中地下水的水井”。陈崇希等编著的《地下水动力学》(第五版)[1]中“地下水三维流场中,常规的(非点状滤管)抽水井或观测孔,不管其置于多层结构还是均质单层结构的含水系统,都属于混合井孔”。陈崇希[1]提到“三维流场中,井管中不同深度的水头是不相等的,因此井管中的水要发生垂直流动,即使在不抽水的观测孔中也一样”。由于自然界中的地下水流大多为三维流,因此,混合井就更普遍了。本文认为“完整或非完整揭露两个及以上含水层的钻孔或水井为混合井”,即揭露以稳定隔水层隔开的两个及以上含水层且其地下水主要以水平或侧向径流形式自由流入“井”中。
由于混合井问题的复杂性,对地下水混合井流相关研究较少。陈崇希[1、3、4]建立了定流量抽水的稳定混合井流模型和不稳定混合井流模型,给出了不抽水时的混合水位(初始混合水位)计算公式,并对定流量混合井抽水问题、地下水渗流-管流耦合问题等进行了研究。王全荣[5]等研究了Modflow软件两种模拟混合井流方法的耦合应用。雷宏武[6]等研究了非均质承压含水层混合井地下水流数值模拟相关问题,提出了改进导水系数——水力梯度法。张学真[7]对利用混合井进行地下水回灌进行了研究。黎明[8]等研究了包括混合井孔的新疆渭干河流域地下水三维不稳定流模型,预测了未来10a不同开采条件下的地下水动态变化规律。宋文玲[9]等研究了水平井和分支水平井与直井混合井的油藏产能计算方法。陈建生[10]等研究了多含水层稳定流非干扰混合多孔井流理论,通过测定各含水层的垂向流速、流向等求解各含水层渗透系数等参数。目前,油藏和水文测井领域对混合井流问题进行了较为深入的研究[11-13],而地下水动力学专业的相关研究缓慢。国际水文地质学家对混合井水文地质概念模型及解析解、数值计算方法及应用等进行了研究,鲜有针对混合井中混合地下水位形成机理与计算方法的相关研究[14-16]。
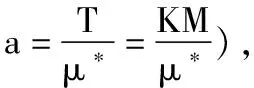
本文通过公式推导得到了揭露两个含水层混合井不抽水状态时的初始混合水位算公式,并在高家堡矿井T1、T2钻孔进行了现场应用,效果较好。
由于混合井在现实生产生活中普遍存在,研究混合井水位问题具有广泛的现实意义。同时,对于进一步揭示巨厚含水层地下水位构成、垂向水文地质参数精细刻画、涌水量精准预测等,混合井水位形成机理是基础理论研究,具有重要的理论意义。
1 混合井初始混合水位形成机理
在不抽(放)水时,混合井内水流是存在垂向流动的。当水位高的含水层地下水流出量(相当于微小流量的定降深抽水试验)和水位低的含水层地下水流入量(相当于微小流量的定水头注水试验)相等时,即可形成初始混合水位。
注:地下水动力学水量计算及数值模拟时,一般假定含水层地下水流出水量为正,流入水量为负。当进行抽(放)水试验时,地下水流出含水层,水量为正值;当进行注水试验时,水流入含水层,水量为负值。因此,在地质与水文地质条件等均不发生变化的情况下,可假定注水井与抽水井水文地质模型类似,仅是水量和降深等正负号有别。
完整揭露两个含水层的混合井初始混合水位形成机理,其实质是假定水位高的含水层进行以初始混合水位为动水位的微小流量定降深抽水试验,假定水位低的含水层进行以初始混合水位为定水头的微小流量注水试验。
以地面抽水混合井为例,研究揭露层状非均质含水层的混合井初始混合水位形成机理。
假定条件:存在上、下两个无界的承压含水层(设想为一半径为R的圆形岛状含水层的情况),其间为隔水层(图1);两个含水层的导水系数分别为T1、T2;初始水头分别为H01和H02(假定H02>H01,均为水柱高度);忽略各层水流在混合井中的水头损失;各层混合井的有效井径相等,rw1=rw2=rw;忽略井筒的储/释水效应。
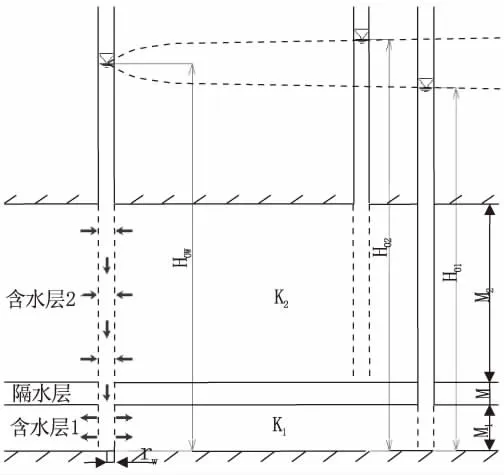
图1 无界含水层混合井未抽水示意图
完全揭露第1、2含水层的混合井,在井中未抽(注)水时可形成初始混合水位H0w,依据上述假定条件H02>H01,必有H02>H0w>H01的关系成立。此时,混合井的水流入第1承压含水层,相当于注水,其井流量为负值,即Q01<0;初始水头较高的第2承压含水层地下水流入混合井,相当于抽水,其井流量为正值,即Q02>0。假定混合井内可形成稳定水位,即初始混合水位H0w,则各含水层的井流量可由定降深、变流量的解析解公式表示,且含水层1从混合井得到的水量等于含水层2向混合井流出的水量,即Q01+Q02=0。
承压水向完整井稳定运动的Dupuit公式为:
混合井中含水层1和含水层2的Dupuit计算公式为:
依据水均衡原理,有:
Q01(t)+Q02(t)=0
所以
化简后移项得到:
由于Sw1=H01-H0w,Sw2=H02-H0w,故有:
由此,本文得到混合井中的初始混合水位H0w的计算公式为:
(1)
式中:η为本文称之为影响半径系数,无量纲;
η计算公式为:
(2)

在混合井初始混合水位的计算公式中,包含有影响半径的参数,而影响半径的计算又是需要由初始混合水位计算的水位降深。通过计算机编程或excel软件,首先给初始混合水位赋初值,通过多次迭代计算可以得到符合初始混合水位误差要求的数值。
同时,在已知两个含水层混合水位和其中一个含水层水位时,可先给所求含水层水头赋值,通过多次迭代计算可以得到符合初始混合水位误差要求的数值。
特别说明:上文中的H01、H02、H0w等是指自最下含水层底界起算的含水层水头,即水柱高度。
2 案例应用
高家堡矿井位于黄陇侏罗纪煤田彬长矿区;设计生产能力为5.0 Mt/a,服务年限62.5 a;首采工作面于2015年12月份开始回采,至2016年4月底回采结束;主采侏罗系延安组4#煤层,采用综采放顶煤采煤工艺。
高家堡矿井采煤活动主要受到煤层上覆白垩系含水层(图2)涌水影响和水害威胁。首采面回采期间最大涌水量为1 199.00 m3/h,采后初期稳定涌水量为838.00 m3/h;涌水的主要构成即为洛河组含水层水[17]。
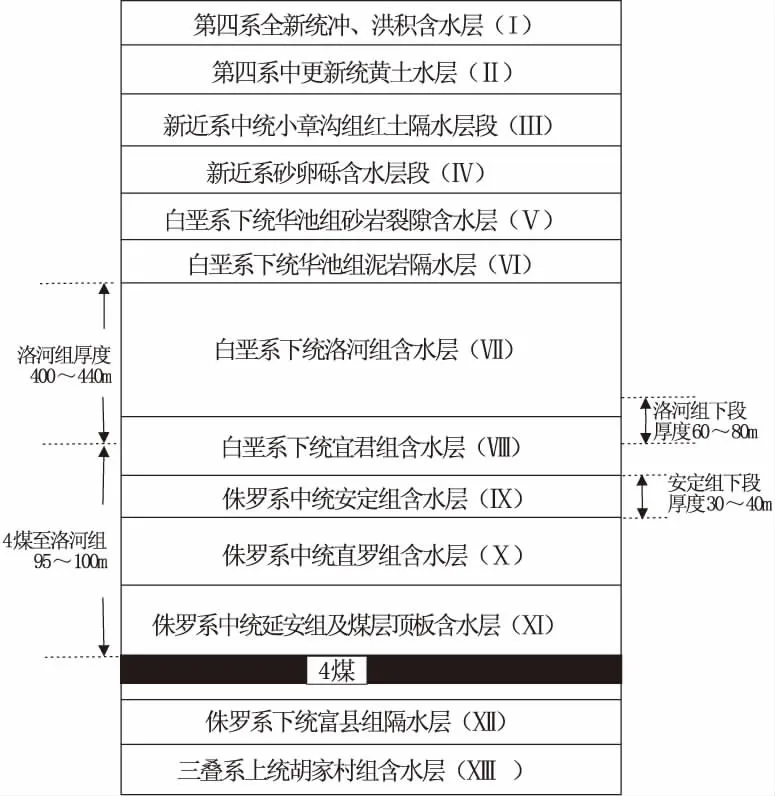
图2 高家堡井田煤层与主要含隔水层位置关系图
为查明井田内主要含、隔水层水文地质条件、预测矿井涌水量,科学制定防治水技术对策等,“高家堡矿井首采区白垩系含水层精细勘探研究”项目实施。施工了T1、T2两个地面钻孔(图3),并进行洛河组全段、上段、中上段、下段等单孔抽水试验和多孔抽水试验,获取了大量第一手数据资料[18、19]。
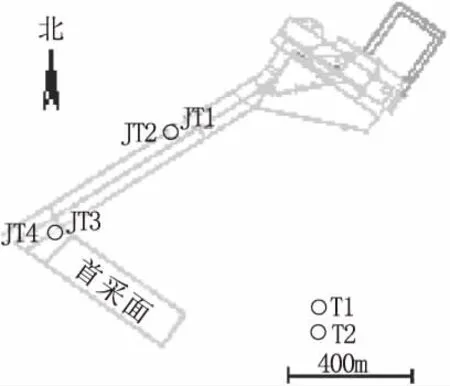
图3 高家堡井田水文补勘钻孔平面位置示意图
由于现场施工条件等影响,未能进行洛河组中段抽水试验,缺少洛河组中段地下水位等数据。因此,可利用本文推导得到的公式计算获得洛河组中段地下水位。
首先,利用T1钻孔洛河组中、上段和下段地下水位,计算混合后的洛河组全段地下水位,并通过与实测水位对比验证本文获得公式的准确性。其次,利用T2钻孔洛河组中、上段和上段地下水位数据,计算得到洛河组中段地下水位。
2.1 计算T1钻孔洛河组全段地下水位
已知T1钻孔洛河组中、上段和下段地下水位,可计算洛河组全段地下水位。采用T1钻孔洛河组中、上段和下段的水头,利用式(1)通过Excel软件迭代计算(误差标准为初始混合水位赋值和计算值之差的绝对值小于0.000 1 m)得到洛河组全段的水头和水位标高(表1)。

表1 T1钻孔洛河组全段混合水位计算
计算T1钻孔洛河组全段地下水位标高为+927.399 0 m。这与该钻孔实测的洛河组全段地下水位+927.74 m相近[18、19],验证了计算结果的准确性。通过与洛河组中、上段地下水位标高(+927.40 m)对比分析,T1钻孔洛河组中、上段地下水位与全段地下水位相近,误差率仅为0.000 1%。因此,洛河组中、上段地下水位可以近似代表洛河组全段地下水位。
2.2 计算T2钻孔洛河组中段地下水位
已知T2钻孔洛河组中、上段和上段地下水位,计算T2钻孔洛河组中段地下水位。首先给洛河组中段水头赋值,利用式(1)通过Excel软件迭代计算(误差标准为实际混合水位和计算值之差的绝对值小于0.000 1 m)得到其水头和地下水位(表2)。
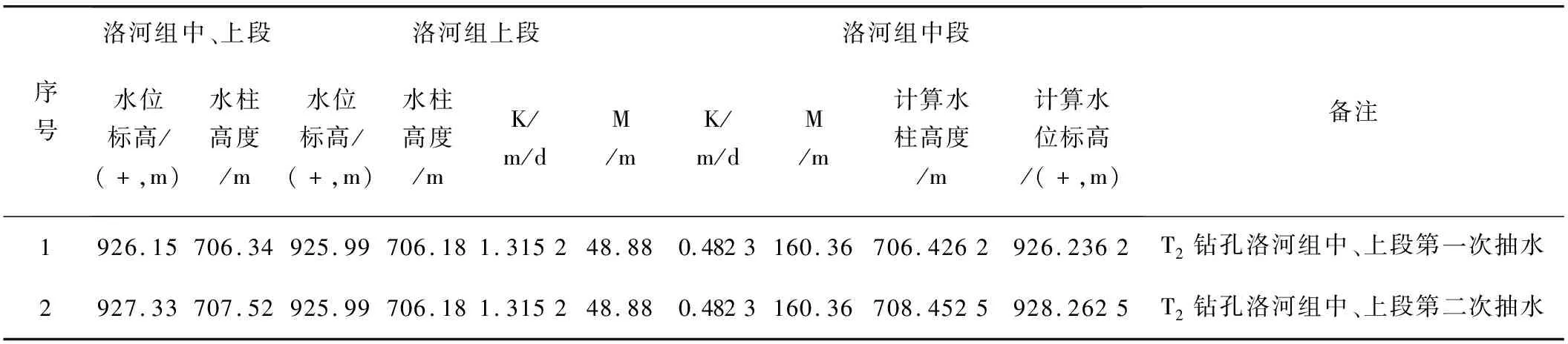
表2 T2钻孔洛河组中段水位计算
计算T2钻孔洛河组中段地下水位标高为+926.236 2 m和+928.262 5 m。这与勘探得到的高家堡井田洛河组中段地下水位高于上段(+925.99 m)的认识一致[18、19],也验证了计算结果的准确性。
3 结语
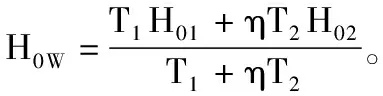
(2)应用本文得到的混合井初始混合水位计算公式,计算了高家堡矿井T1钻孔洛河组全段地下水位和T2钻孔洛河组中段地下水位。通过对比分析,验证了本文推导得到的初始混合水位计算公式的正确性。
(3)在不抽(放)水时,混合井内水流是存在垂向流动的。完整揭露两个含水层的混合井初始混合水位形成机理,其实质是假定水位高的含水层进行以初始混合水位为动水位的微小流量定降深抽水试验,假定水位低的含水层进行以初始混合水位为定水头的微小流量注水试验。当揭露含水层数量大于2个时,或者为非完整揭露2个含水层的混合井,其初始混合水位形成机理还需要继续深入探索。
