基于SCHISM模式的全球潮波模拟
2021-08-27涂成东纪棋严左军成
涂成东,纪棋严,左军成
(浙江海洋大学 海洋科学与技术学院,浙江 舟山 316022)
潮波运动是地球流体动力学过程的重要组成部分,海洋中的诸多物理过程都与其紧密相关,这既影响着全球海洋的地形、海岸线的塑造,又影响着人类的生产、生活以及生态环境,尤其在近海环境研究、航运交通、资源开发、军事活动等方面。因此,研究全球海洋潮波的分布规律具有重要的理论和现实意义。
20世纪80年代,全球大洋潮波模式开始兴起。SCHWIDERSKI[1-2]将流体动力学方程和实测调和常数相结合,拓展了 Laplace潮汐理论,构建了首个全球潮波模式 Schw80。Schw80能给出 M2、S2、N2、K2、K1、O1、P1、Q1、Ssa、Mm和 Mf共 11 个分潮的同潮图,这对于全球潮波的研究具有开创性的意义。1985年Geosat卫星发射升空,卫星高度计资料开始被人们应用到全球大洋潮波的研究当中。CARTWRIGHT等[3-4]根据Geosat卫星高度计资料构建了第一个基于卫星高度计的全球大洋潮波模式,研究了混淆对潮汐分离的影响,并且对M2和S2分潮计算结果与一些沿岸观测结果进行了比较。FANG等[5]利用 Geosat卫星高度计资料,采用准调和分潮的方法计算了全球M2、S2、K1、O1、M4和 MS4分潮调和常数。1992 年美国国家航空航天局(NASA)和法国国家空间研究中心(CNES)合作研发的topex/poseidon(简称T/P)卫星发射以后,人们获得了大量高精度海表面高度数据,极大地推动了全球潮波的研究以及潮波模型的发展[6]。 ANDERSEN[7]利用1.5年长度的 ERS卫星和T/P卫星高度计数据,计算得到了全球大洋M2、S2、N2、K2、K1、O1、P1和 Q1这 8 个主要分潮的调和常数,建立了分辨率为 0.75°×0.75°的潮波模型。PROVOST等[8]将CARTWRIGHT等所使用的方法应用于高精度T/P数据处理上,分离了8个主要分潮和3个长周期分潮,得到了比Cartwright等更为精确的计算结果。由于 T/P卫星高度计带来的巨大影响力,越来越多基于T/P卫星高度计的全球模型出现,如法国的 FES[9-10]模式,美国的 CSR[11]、GOT[12]、OSU[13]和 TPXO[14]模式,日本的 NAO[15]模式,德国的ETO[16]和HAMTIDE[17],丹麦的DTU模式[18]。SHUM等[19]从多个方面评估了1994年之后发展的10种大洋潮波模式,结果表明这些模式的精确度很高,尤其在深水区,相较于Schw80模式有了长足的进步。汪一航等[20]基于 152个深海验潮站和大洋岛屿地面验潮站得到的8个主要分潮调和常数,对7种大洋潮波模式(SCW80、CSR4.0、FES2002、FES2004、GOT00、NAO99、TPXO7)在太平洋、印度洋和大西洋的精确度进行评估,结果表明各模式的 8个分潮之和的总体准确度达到了 95%左右。李大炜等[21]利用传统验潮站数据对 5个全球海洋潮波模型NAO.99b、FES2004、GOT4.7、TPXO7.2和 EOT10a进行精度评估,结果表明现在的全球海洋潮波模型相比早期的海潮模型均取得了较大进步,在深海海域,模型精度达到了2 cm,空间分辨率为50 km。
目前的全球大洋潮波模式主要分为两类,一类是基于卫星测高数据的经验模式,从测高卫星数据中提取潮汐信息; 另一类是基于流体动力学方程,按照特定的优化标准和方法,将观测数据和数值模型结合起来的同化模式。同化模式由于其将观测结果与物理学模型相结合起来的特点,能够有效提高潮波模式的分辨率和精确度。潮波动力模式作为同化模式的基础,能够较为准确地模拟全球大洋的潮波特征,对于全球大洋潮波模式的建立至关重要。于华明[22]基于非结构网格有限体积法海洋模式(finite volume coastal ocean model,FVCOM),建立了无结构三角形可变网格全球海洋潮汐模型,该模型成功地模拟了全球海洋以及中国近海潮波特征。肖斌[23]基于大洋环流模式 MOM4,在中等分辨率和涡相容分辨率下对全球正压潮波进行了模拟研究,建立了一个水平分辨率为 1/4°的全球潮波模型。本文基于非结构网格半隐式跨尺度海洋模式(semi-implicit cross-scale hydroscience integrated system model,SCHISM),把全球大洋作为一个整体,进行了高分辨率的潮波数值模拟,利用潮位站资料和3个全球模型(TPXO8、FES2014b和NAO.99b)对模拟结果进行验证对比,结果良好,证明了模型的可靠性。在此基础上,系统研究全球大洋潮波的分布特征。
1 模式简介
SCHISM 模式是原始 SELFE模型的衍生作品,是一个基于非结构化网格(UG)的 3D无缝跨尺度模型,用于流体动力学和生态系统动力学。它使用一种高效且准确的半隐式有限元/有限体积方法和欧拉-拉格朗日算法来求解 Navier-Stokes方程(静水压形式),降低了模式的稳定性约束,从而能够进行复杂的数值模拟。数值算法将高阶和低阶方法混合在一起,以有效的方式获得稳定而准确的结果。质量守恒通过有限体积传输算法来实现。此外,该模型还具有以下特点: 水平方向为非结构混合三角形/四边形网格,一方面可以拟合复杂岸线,另一方面可以加密重点海域,平衡分辨率与计算量之间的矛盾; 垂直方向可以采用混合SZ坐标系或者新LSC2坐标系,有利于处理复杂地形变化; 半隐式时间步进(无模式拆分),无CFL稳定性约束,可以提高数值效率; 动量对流的高阶欧拉-拉格朗日处理(带ELAD滤波器); 在非涡流状态下对质量不高的网格具有极高的适应性。
SCHISM模式的控制方程如下:
动量方程为:

3D和2D深度积分形式的连续性方程为:
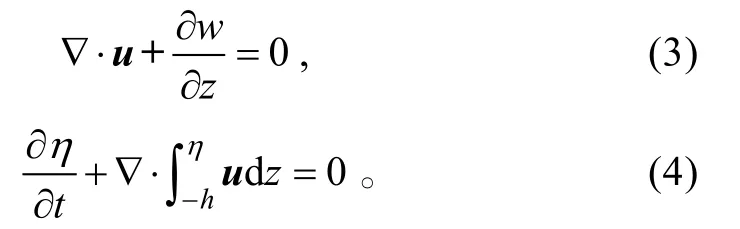
输运方程为:
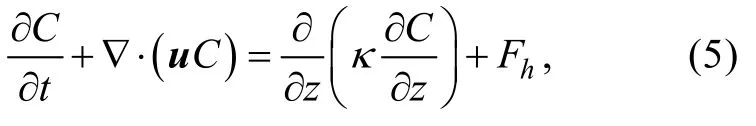
状态方程为:

式中,(x,y)为水平笛卡尔坐标,z为垂直坐标(向上为正),t为时间,η(x,y,t)为自由表面高度,h(x,y)为测量深度(从固定基准测量),u(x,y,z,t)为水平速度,w(x,y,z,t)为垂向速度,p为静水压强,pA为平均海平面的大气压强,ρ为水体密度,ρ0为参考水体密度,f为动量中的其他强迫项(斜压梯度、水平黏度、科氏力、潮汐势、大气压、辐射应力),g为重力加速度,C为示踪剂浓度(盐度、温度),v为垂直涡动黏性系数,к为示踪剂的垂直涡动粘性系数,Fm为水平黏度,Fh为水平扩散和质量源,other为辐射应力。
SCHISM模式的引潮势如下:
半日潮(M2、S2、N2、K2)为:

全日潮(K1、O1、P1、Q1)为:

式中,λ为地理经度,φ为地理纬度,C为分潮振幅,v为分潮迟角,T为分潮周期,f为交点因子。
2 模型设置和验证
本文计算区域为全球海洋,包括太平洋、大西洋、印度洋、北冰洋以及几乎所有陆架浅海和边缘海。网格共有 97 703个网格节点和 187 873个三角单元。由表1可以看出,网格在各大洋东边界较西边界稀疏,这是基于潮波波长和水深的原因。浅海边缘海、北极等海域的网格也得到了加密,这考虑到了全球大洋的整体变化与各海区之间的相互影响。利用非结构三角网格对重点海域加密的特点,很好地平衡了模型分辨率与计算量之间的矛盾。垂直方向采用纯sigma坐标系统,水深分为11层。水深资料来自美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)数据中心的GEBCO 格点化水深数据,分辨率为 0.5′×0.5′,通过反距离加权法(Inverse Distance Weighted)插值求得各网格点的水深,图1给出了计算区域的水深分布。

表1 各海域网格分辨率分布表Tab.1 Grid resolution distribution table for each sea area

图1 模型水深分布及潮位站位置分布Fig.1 Water depth distribution of the model and the location distribution of tidal stations
模型由 8 个天文分潮 K1、O1、Q1、P1、M2、K2、N2、S2作为驱动力,按公式(7)~(8)的形式添加到动量方程当中,各分潮属性如表2所示。图2所示为模型运行30 d得出的整个模拟区域内总动能随时间的变化情况。可见,模型总动能到 15 d左右达到最大,并已基本达到稳定状态,故可确定模型运行20 d后已完全稳定。取稳定后180 d的时间序列进行调和分析,足以准确计算得到M2、S2、K1、O1这4个主要分潮的调和常数[24]。为验证模型的准确性,本文采用夏威夷大学海平面中心提供的 196个站点的全球海洋观测系统(the global sea level observing system,GLOSS)逐时数据,这些数据得到了全面的质量控制并被认为是最终的科学数据集,通过调和分析得到各站点的分潮调和常数。潮位站的分布如图1所示,其中太平洋包含91个站点,大西洋包含75个站点,印度洋包含30个站点,具体位置见表3。

表2 模型8个主要分潮属性表Tab.2 Eight main tidal component attributes of the proposed model

图2 模型全场动能的时间变化曲线Fig.2 Time variation curve of the total kinetic energy of the proposed model
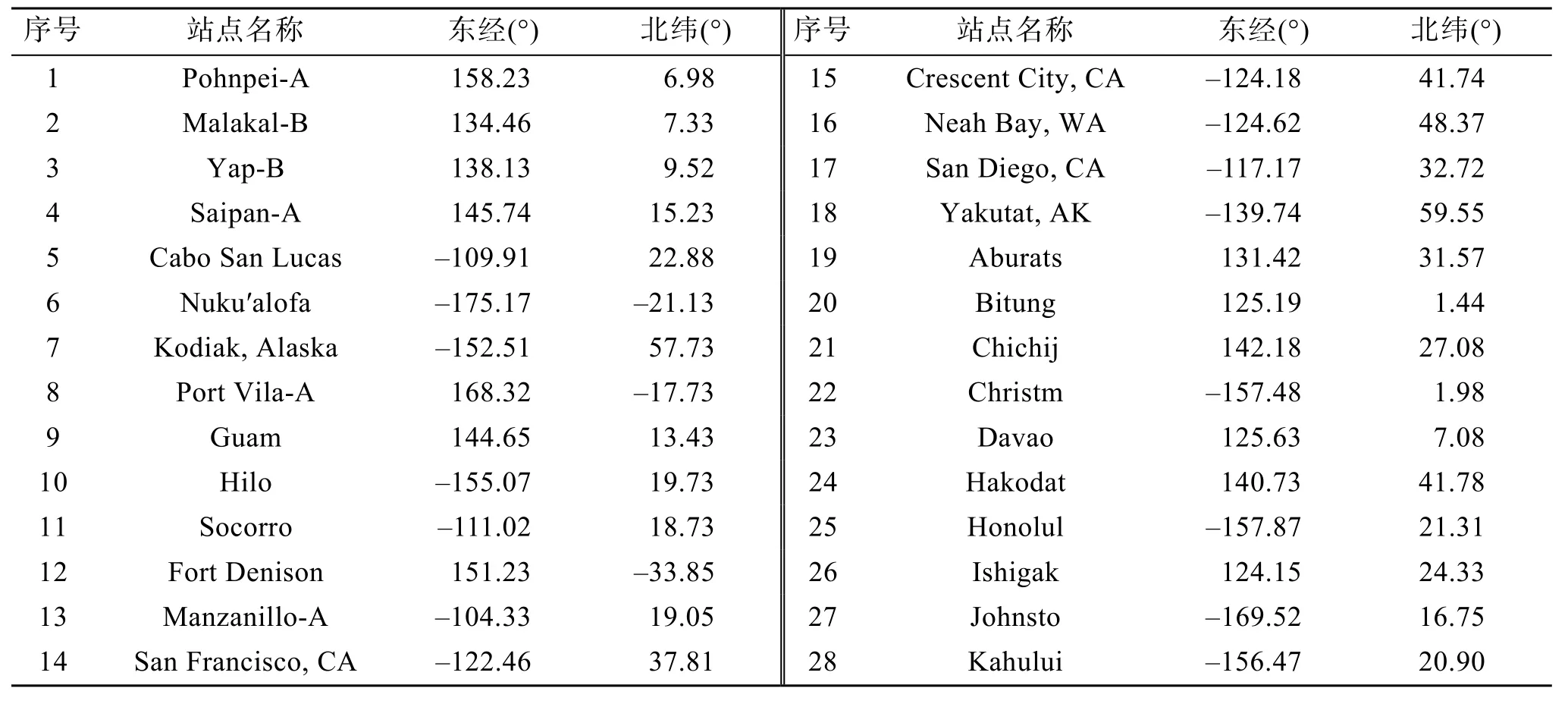
表3 全球大洋196个潮位站的经纬度坐标Tab.3 Latitude and longitude coordinates of the 196 tidal stations in the global ocean

续表

续表
模型模拟结果与潮位站的 4个主要分潮的调和常数对比如图3所示。由表4可知,全球大洋整体范围,M2分潮振幅绝对平均偏差小于8 cm,相位绝对平均偏差小于20°; S2分潮振幅绝对平均偏差小于4 cm,相位绝对平均偏差小于27°; K1分潮振幅绝对平均偏差略大于3 cm,相位绝对平均偏差小于25°; O1分潮振幅绝对平均偏差小于 3 cm,相位绝对平均偏差略大于 24°。三大洋中,太平洋的模拟结果最好,大西洋和印度洋在相位上的偏差较大。由于较多数量的验潮站位于近岸海域,网格分辨率较粗以及水深数据精确度不足等因素导致模型模拟的结果在这些位置偏差较大,但从总体上看,模型模拟结果较好。
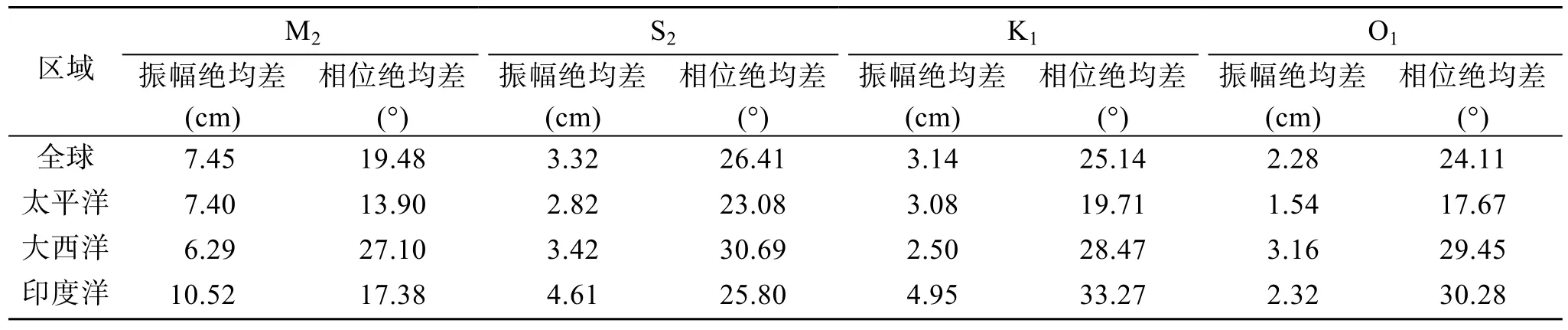
表4 4个主要分潮在各海区模拟结果检验Tab.4 Verification of simulated results for the four main tidal components in various sea areas
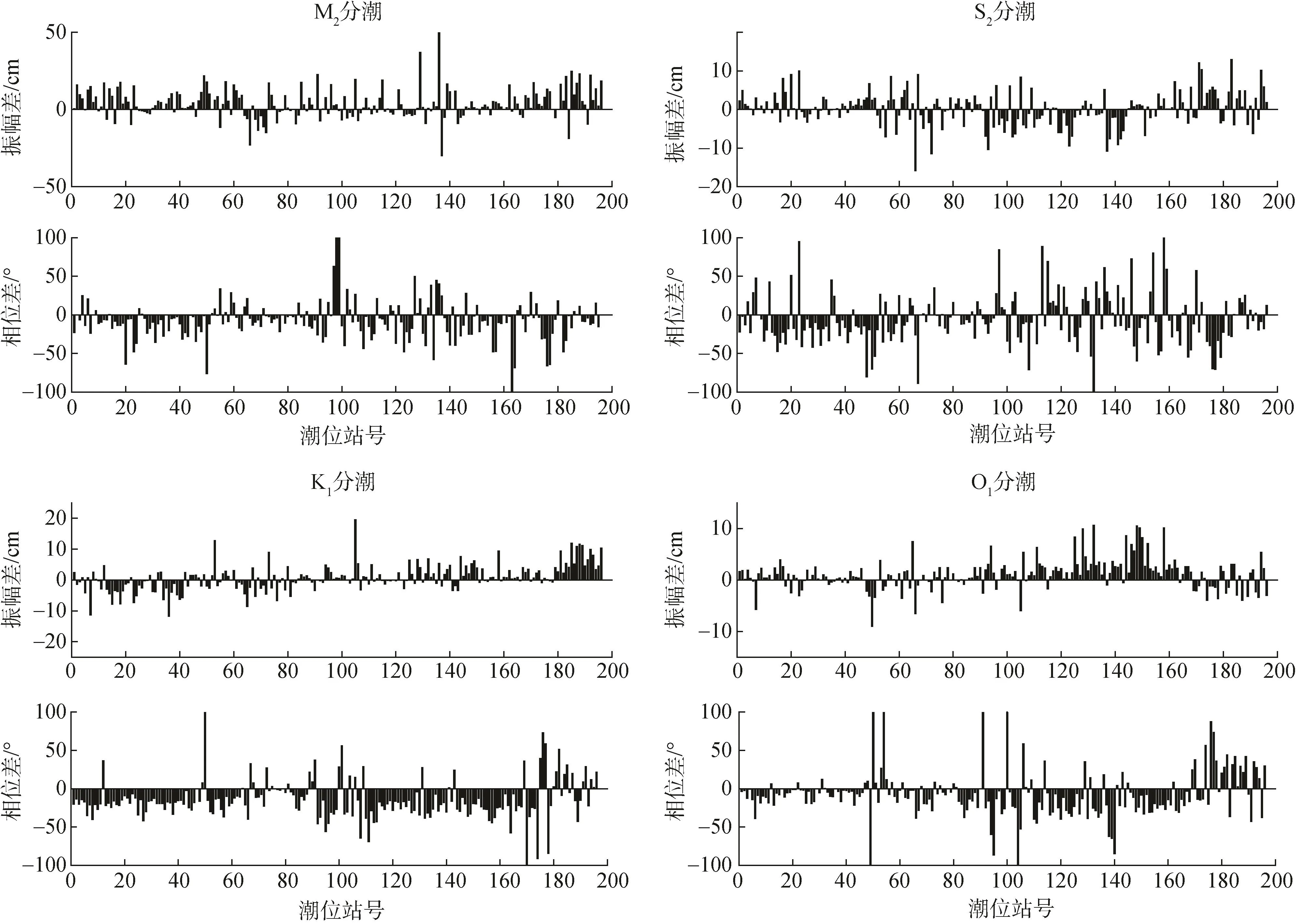
图3 各潮位站分潮调和常数的观测值与计算值之差Fig.3 Difference between the observed and calculated values of tidal harmonic constants at each tidal station
3 模拟结果分析
模型模拟的M2分潮同潮图与TPXO8、FES2014b、NAO.99b模型的 M2分潮同潮图如图4所示,可以看出,3个对比模型之间差别极小,潮波的分布形态几乎相同。本模型的模拟结果较为吻合,北半球模拟结果普遍较南半球好,只是在局部海域无潮点的数量和位置有所偏差,这主要是由于网格分辨率不足和地形数据不准确造成的。在太平洋中分布有 8个较为独立的旋转潮波系统,其中北纬30度以北为1个顺时针旋转无潮点和1个逆时针旋转无潮点,这2个无潮点在对比模型中不存在。北太平洋的 1个逆时针旋转潮波系统位于北美洲西部海域,1个顺时针旋转潮波系统位于科隆群岛西部海域。南太平洋中,位于大洋中部的 1个无潮点为逆时针旋转潮波系统,位于南美洲西部海域的 1个无潮点为顺时针旋转潮波系统。60°S以南的2个顺时针旋转无潮点在对比模型中不存在,而在对比模型中位于罗斯海和南极洲玛丽伯德地附近海域的无潮点没有被模拟出来。在大西洋中分布有 4个较为独立的旋转潮波系统,3个逆时针旋转潮波系统分别位于纽芬兰岛东部、加勒比海东部和南美洲东部,1个顺时针旋转潮波系统位于南极洲毛德皇后地附近海域。相比于对比模型,主要区别在于南极洲毛德皇后地附近海域的无潮点位置偏东。印度洋中共有3个独立旋转潮波系统,皆呈顺时针旋转,分别位于阿拉伯海、澳洲西部以及澳洲南部海域,其中位于澳洲南部的无潮点在对比模型中不存在。在对比模型中,位于60°E、南极洲毛德皇后地近岸海域还存在1个顺时针旋转无潮点。

图4 模型模拟结果与3个全球大洋模型的M2分潮同潮图Fig.4 Cotidal charts of the global M2 tidal component from the model simulation results and three global ocean models
赤道太平洋海域出现两个M2分潮高振幅区,其振幅均超过40 cm,甚至60 cm。总体上来说,M2分潮在北太平洋和北大西洋东岸附近海域的振幅大于西岸附近海域的振幅,而在南太平洋和南大西洋情况相反。
S2分潮的空间分布如图5所示。总体上看,S2分潮与M2分潮的空间分布极为相似,只是振幅相对较小。太平洋中共有8个明显的无潮点,其中北太平洋4个,2个顺时针旋转潮波系统分别位于东北太平洋和科隆群岛西部海域,2个逆时针旋转潮波系统分别位于北美洲西部和阿留申群岛西部海域。南太平洋中,3个顺时针旋转潮波系分别位于德雷克海峡、南美洲西部和新西兰东南部海域,唯一的 1个逆时针旋转潮波系统位于大洋中部。大西洋中共有4个明显的无潮点,其中3个为逆时针旋转潮波系统,分别位于纽芬兰岛东部、加勒比海东部和南美洲东部海域,1个顺时针旋转潮波系统位于南极洲毛德皇后地附近海域。印度洋中共有3个明显的无潮点,分别位于阿拉伯海、澳洲西部以及澳洲南部海域,皆为顺时针旋转潮波系统。S2分潮在北太平洋和北大西洋东岸附近海域的振幅较其在西岸附近海域的振幅大。在大洋中40°S以南海域S2分潮的等振幅线稀疏,振幅较小。

图5 全球S2分潮同潮图Fig.5 Cotidal chart of the global S2 tidal component
模型模拟的K1分潮同潮图与TPXO8、FES2014b、NAO.99b模型的 K1分潮同潮图如图6所示,可以看出,3个对比模型之间差别极小,潮波的分布形态几乎相同。本模型模拟结果与其主要差别位于印度洋和南大西洋海域。太平洋中共存在 5个明显的无潮点,其中位于0纬度线附近的3个无潮点彼此相连,由西向东依次为逆时针、顺时针和逆时针旋转潮波系统,其余2个无潮点为顺时针旋转潮波系统,分别位于新西兰岛东南部和新西兰岛与澳洲之间海域,后者在对比模型中不存在。大西洋中分布有3个无潮点,位于30°N附近的1个为逆时针旋转潮波系统,位于0纬度线附近、南美洲东部的 1个为顺时针旋转潮波系统,该无潮点相对于对比模型中的对应无潮点位置偏西北。还有1个为顺时针旋转潮波系统位于南纬40度、特里斯坦-达库尼亚群岛附近海域,该无潮点在对比模型中不存在。印度洋中分布有1个顺时针旋转潮波系统和1个逆时针旋转潮波系统,前者位于马达加斯加东部海域,后者位于斯里兰卡南部海域。在对比模型中,斯里兰卡南部海域存在1个逆时针旋转无潮点,另一个顺时针旋转无潮点位于30°E、50°S附近海域。

图6 模型模拟结果与3个全球大洋模型的K1分潮同潮图Fig.6 Cotidal charts of the global K1 tidal component from the model simulation results and three global ocean models
K1分潮的振幅普遍较小,在大部分海域不超过30 cm,在北太平洋和南极洲附近海域,由大洋向近岸有增加的趋势。
O1分潮的空间分布如图7所示。太平洋中共分布有4个明显的无潮点,大洋中部的2个无潮点彼此相连,其中位于 0纬度线附近的无潮点为逆时针旋转潮波系统,位于 20°S附近的无潮点为顺时针旋转潮波系统,另外 2个顺时针分别位于新西兰北部和南部海域。大西洋中分布有2个无潮点,其中位于北纬30度以北的无潮点为逆时针旋转潮波系统,位于30°S以南的无潮点为顺时针旋转潮波系统。印度洋中分布有 2个明显的无潮点,分别位于马达加斯加东部和斯里兰卡东部海域,前者为顺时针旋转潮波系统,后者为逆时针旋转潮波系统。O1分潮的振幅与K1分潮的情况类似,普遍偏小,

图7 全球O1分潮同潮图Fig.7 Cotidal chart of the global O1 tidal component
在绝大部分海域不超过20 cm,在北太平洋和南极洲附近海域,由大洋向近岸有增加的趋势。
4 结果与讨论
本文基于SCHISM海洋数值模式,采用非结构三角网格,将全球大洋联系为一体,进行高分辨率潮波数值模拟研究,模拟结果与实测数据吻合良好,M2、K1分潮同潮图的分布形态与 TPXO8、FES2014b和NAO.99b模型给出的相似。根据模拟结果,给出了M2、S2、K1、O1这4个主要分潮同潮图。主要结论如下:
太平洋共存在8个M2分潮无潮点,北太平洋中为2个逆时针旋转潮波系统和2个顺时针旋转潮波系统,南太平洋中为3个顺时针旋转潮波系统和1个逆时针旋转潮波系统。大西洋中存在4个M2分潮无潮点,其中3个为逆时针旋转潮波系统,1个为顺时针旋转潮波系统。印度洋中存在3个M2分潮无潮点,皆为顺时针旋转潮波系统。总体上来说,M2分潮在北太平洋和北大西洋东边界的振幅总要大于边界的振幅,而在南太平洋和南大西洋情况相反。S2分潮分布特征与M2分潮类似,但振幅较小。
太平洋中存在5个K1分潮无潮点,其中2个为逆时针旋转潮波系统,3个为顺时针旋转潮波系统。大西洋中存在1个逆时针旋转潮波系统和2个顺时针旋转潮波系统。印度洋中存在 1个顺时针旋转潮波系统和 1个逆时针旋转潮波系统。K1分潮的振幅普遍较小,在大部分海域不超过30 cm,由大洋向近岸有增加的趋势。太平洋中存在4个O1分潮无潮点,其中3个为顺时针旋转潮波系统,1个为逆时针旋转潮波系统。大西洋中分布有 1个逆时针旋转潮波系统和1个顺时针旋转潮波系统。印度洋中分布有1个逆时针旋转潮波系统和 1个顺时针旋转潮波系统。O1分潮振幅情况与 K1分潮类似,但振幅较小,在大部分海域不超过20 cm,在北太平洋和南极洲附近海域,由大洋向近岸有增加的趋势。
本文的模拟结果在精度上还有一定提升的空间。RAY等[25]认为,不精确的水深数据以及未知的摩擦和黏度参数尤其影响水动力模型的精度。KANTHA[26]还指出,如果不对控制参数(如底部摩擦)进行大范围的微调,则很难准确地获得潮波模型,尤其是其相位模型。本模型近岸网格分辨率较低且直接采用国际上的全球测深数据,缺乏对近岸水深的订正,导致近岸模拟结果不理想,这点在与验潮站数据的对比中体现明显。同时,在与3个对比模型的同潮图比较中,无潮点的数量和位置也出现一定偏差,除去以上的因素外,还有 1个很重要的原因在于本模型没有考虑到海水自吸引与负荷潮效应。HENDERSHOTT[27]指出全球潮波的模拟需要考虑海水自吸引与负荷潮效应,这是由潮汐引起的地球形变和海水质量重新分布导致的引潮势的变化产生的综合效应。最后是缺少同化对模型精度的提高,尽管罗斯海水深数据不足且常年覆盖冰层,TPXO8和FES2014b模型还是成功模拟出了位于其中的M2分潮无潮点,这是由于这2个模型同化了该地区的验潮站数据,使得精度大为提高。
