基于逐步回归和SVR方法的上海夏季日最大电力负荷的模拟研究

李 艳， 徐卫立， 裴顺强， 范晓青， 赵良水， 李长春

(1.中国气象局公共气象服务中心，北京100081； 2.智慧长江与水电科学湖北省重点实验室，湖北 宜昌443133； 3.中国气象局办公室，北京100081； 4.长江生态环保集团有限公司，重庆401120)

引 言

气候变化加剧带来极端高温事件频发，特别是一些超大型城市夏季持续高温，城市电网负荷不断突破历史极值，不仅给电网运行带来巨大压力，还可能造成输变电设备因超载运行发生故障。电网负荷变化受多种因子影响，关系也比较复杂，其中气象要素与电力负荷的关系极为密切[1-5]。张自银等[6]研究指出，北京市夏季日最低气温与逐日最大电力负荷的关系最为密切，同时夏季温度和湿度的综合效应比单个温度因子对电力负荷波动的贡献率更高。准确的电网负荷预测有助于电网及相关输供电单位提前采取有效的发电计划和调度措施，对于保障电网和城市的安全运行非常重要，同时也能减少能源浪费，给电力市场带来巨大的经济效益。

前人针对气象条件与电力负荷的关系及其预测做了大量研究[7-14]。胡江林等[15]从华中电网电力负荷资料中分离出随气象因子变化的气象负荷，重点分析了气象负荷随气温变化的规律。李琛等[16]研究指出，北京市夏季日最大电力负荷与闷热指数及平均气温的相关性最好，同时气象因子对夏季电力负荷的影响存在“多日累积效应”，持续2天的闷热将导致电力负荷急剧增加。成丹等[17]基于积温效应开展了华中电网电力负荷预测，结果表明持续3天以上的炎热天气过程对华中电网电力负荷增长影响显著，其中湖北的电力负荷增量最大。此外，近年来在电力、供水及其他相关领域采用机器学习等多种方法开展预测的研究也越来越多[18-27]，其中支持向量机回归模型具有较好的泛化预测及自适应能力，非常适用于存在非线性、多变量、不确定性的电力负荷预测，能有效地提高负荷预测精度。

虽然许多学者针对电网和市场需求开展了日最大电力负荷预测的工作[28-29]，但由于区域间气候条件、经济结构和发展水平不同，电网电力负荷与气象因子的关系不尽相同。因此本研究以上海这个对电力安全运行能力要求极高的超大型城市为对象，针对用电高峰的夏季，基于多种影响因子采用逐步回归和支持向量回归(SVR)模型两种方法来构建日最大电力负荷关系模型，以期为准确预测上海市夏季日最大电力负荷提供技术参考。

1 资料和方法

1.1 资料来源

本研究所用电力负荷资料为上海2013-2017年逐日96点统调负荷数据，有效数据共1826天,气象资料为上海各区县的日平均气温、日最高气温、日最低气温、日平均相对湿度、日最小相对湿度、日降水量等气象要素。上海地区电网所辖区域为浦东、市区(虹口、静安、黄浦、长宁、杨浦)、市北(宝山)、市南(徐家汇)、嘉定、青浦、松江、金山、奉贤、崇明和长兴，这些地区气候条件相似，但用电负荷差异显著。据电力调度部门统计，近年来浦东用电负荷最大，占上海统调负荷的20%以上，崇明和长兴用电负荷最少，仅占1%左右，其余区县所占比例为5%～15%。为更加科学合理地计算上海电网区域气象条件对电力负荷的影响，根据各区县用电负荷所占比例，取各区县气象要素的加权平均值代表上海市电网的气象条件。本研究把2013-2016年的数据用于模型的构建,2017年的数据用于模型的验证。

1.2 炎热累积效应指数

前人研究表明，夏季持续高温过程中，同等气温条件下，电力负荷会随着持续时间增加而出现较大程度的增长，称为炎热累积效应，是电力负荷预测建模中非常重要的自变量。炎热累积效应指数不仅与超过临界值的日数有关，还与超过临界值的大小有关。由于炎热累积效应指数的计算结果存在很大的值跳跃，本研究在前人研究基础上[30]，对炎热累积效应指数进行了一次对数变换，使分布更加均匀，便于建模。计算方法如下：

Y=ln[n(Tm-T0)+1]

(1)

式中，Y为经过对数变换后的炎热累积效应指数，单位为℃·d；n为超过最高气温临界值的累计日数，Tm为当日最高气温，T0为对应的最高气温临界值。当气温未达到临界值时，n为0；当气温超过某一临界值日起，n从1开始逐日累加，依次循环。

1.3 天气敏感负荷的分离

为了准确分析气象条件对用电负荷的影响，需要将气象负荷分离出来，然后根据生产活动和气象条件变化，分离分段进行分析研究。

一般来说，用电负荷由三个分量组成：

L=Lt+Lm+x

(2)

其中，L为总用电负荷；Lt为经济负荷，也称为趋势负荷，表示国民经济发展对用电负荷的贡献;Lm为天气敏感负荷，表示气象要素对用电负荷的贡献；x为随机负荷，表示随机因素对用电负荷的影响。

对于原始用电负荷数据序列L，进行以7天为周期的滑动平均，删除以星期为周期的波动分量，得到滑动平均负荷序列TCt：

(3)

式中，k表示滑动周期，t表示天数。

国民经济增长速度一般比较均匀，因此经济负荷随时间的变化可以用简单的线性关系来表示。对滑动平均负荷序列TCt进行线性拟合，采用最小二乘法确定系数a和b，得到经济负荷Lt的线性回归方程，从而求得经济负荷序列Lt：

Lt=a+bt

(4)

由于随机负荷与其他项相比，量级小且随机性强，影响较小，在此忽略不计。因此天气敏感负荷Lm为原始负荷L与经济负荷Lt的差值：

Lm=L-Lt

(5)

由于电力部门最为关注的还是用电负荷受天气影响部分的波动比例,因此本文开展气象条件与用电负荷相关性研究时，采用的负荷数据均为天气敏感负荷Lm与经济负荷Lt的比值，即天气敏感负荷率lm：

(6)

1.4 预测模型介绍

1.4.1 逐步回归方法建模

逐步回归是一种线性回归模型自变量选择方法。考虑到用电负荷不仅存在累积效应，而且还存在“记忆性”，即前一天的用电负荷对于次日用电负荷影响很大，因此设计了两种方案来进行逐步回归建模。

方案1：仅根据气象因子建立逐步回归模型；分别计算各个建模因子与日最大天气敏感负荷率的相关系数。根据前人研究，选择日最高气温(x1)、日最低气温(x2)、日平均气温(x3)、日平均风速(x4)、日最大风速(x5)、日平均相对湿度(x6)、日最小相对湿度(x7)、日降雨量(x8)、炎热累积效应指数(x9)这9个气象因子建模。

方案2：在方案1的基础上，引入前一天用电负荷作为自变量建立逐步回归模型。

1.4.2 SVR支持向量回归方法建模

SVR就是在多维空间中找到一个超平面，让一个集合的所有数据到该平面的距离最近。传统回归方法仅当回归f(x)完全等于y时才认为预测正确，而支持向量回归则认为只要f(x)与y偏离程度不太大，即可以认为预测正确，不用计算损失。具体就是设置阈值α,只计算|f(x)-y|>α的数据点的损失，如图1所示，阴影部分的数据点可以认为模型已准确预测，只需计算阴影外数据点的损失。

图1 SVR模型示例图

SVR模型有以下几个参数。

(1)kernel：核函数，可选为rbf、linear、poly、sigmoid。

(2)C：惩罚因子，C越大表明越重视离群点。C值大时对误差分类的惩罚增大，C值小时对误差分类的惩罚减小。当C越大，趋近无穷的时候，表示不允许分类误差的存在，margin越小，容易出现过拟合；当C趋于0时，表示不再关注分类是否正确，只要求margin越大，容易出现欠拟合。

(3)Gamma：是rbf、poly和sigmoid的核系数。随着Gamma的增大，存在对于测试集分类效果差、而对训练分类效果好的情况，并且容易泛化误差出现过拟合。

本研究选择的参数组合为kernel=‘linear’，C=1，Gamma=1。

考虑到原数据集中特征数量太少，不利于模型挖掘内在联系从而进行预测。因此，对于每个原始天气变量，将其前一天的值和过去一周平均值作为两个新的特征加入数据集，体现天气条件对于负荷影响的滞后性和累积性。同时，在日期信息中，将一周中的第几天也作为一个特征，体现一周中负荷的变化。此外，日期类型作为特征，用来体现工作日、双休日、节假日之间负荷水平的差异。扩展后的数据集共有29个特征值(表略)。

2 结果分析

2.1 天气敏感负荷率与温度因子的关系

气温对用电负荷的影响最为直接。把上海2013-2017年工作日的日最大天气敏感负荷率与最高气温进行分段拟合(图 2)。由图 2可知，气温与用电负荷之间的关系是非线性的，呈明显的二次曲线关系，当最高气温小于16 ℃时，随着气温的逐步升高，负荷水平逐步降低；当最高气温为17-23 ℃时，气温处于人体感受的舒适区间内，负荷变化较为平稳；而最高气温高于24 ℃时，随着气温逐步升高，负荷水平逐步上升，且夏季的空调降温负荷明显高于冬季取暖负荷。

图2 上海2013-2017年工作日最大天气敏感负荷率与日最高气温拟合图

2.2 天气敏感负荷率与炎热累积效应指数的关系

2.2.1 炎热累积效应临界值的确定

在电力部门，日最大用电负荷对日最高气温比较敏感。为了确定上海夏季炎热累积效应的气温临界点，采用日最高气温变化跟踪日最大天气敏感负荷率的变化。表1为上海日最高气温升高1 ℃对应的日最大天气敏感负荷率平均值(K)及日最高气温升高1 ℃时K的增加值(M)。

由表 1可知，从27 ℃开始，随着日最高气温的升高，日最大天气敏感负荷率不断升高，在最高气温达到33-34 ℃时，K值达到了33.0%，意味着空调负荷所占比重很大，同时M为9.6%，需引起重视，可以认为是初始气温敏感点；在温度达到35-36 ℃时，K值达到了43.0%，M为6.1%，可以认为是强气温敏感点；在气温达到37-38 ℃时，K值和M值分别为49.8%和7.7%，说明气温再升高1 ℃,天气敏感负荷率的平均值达50%以上，此时，可能由于制冷设备长时间大量运转出现一些开关跳闸、被烧等电力事故，电力部门需警惕重视。由此可以确定上海夏季炎热累积效应的临界值为33 ℃。

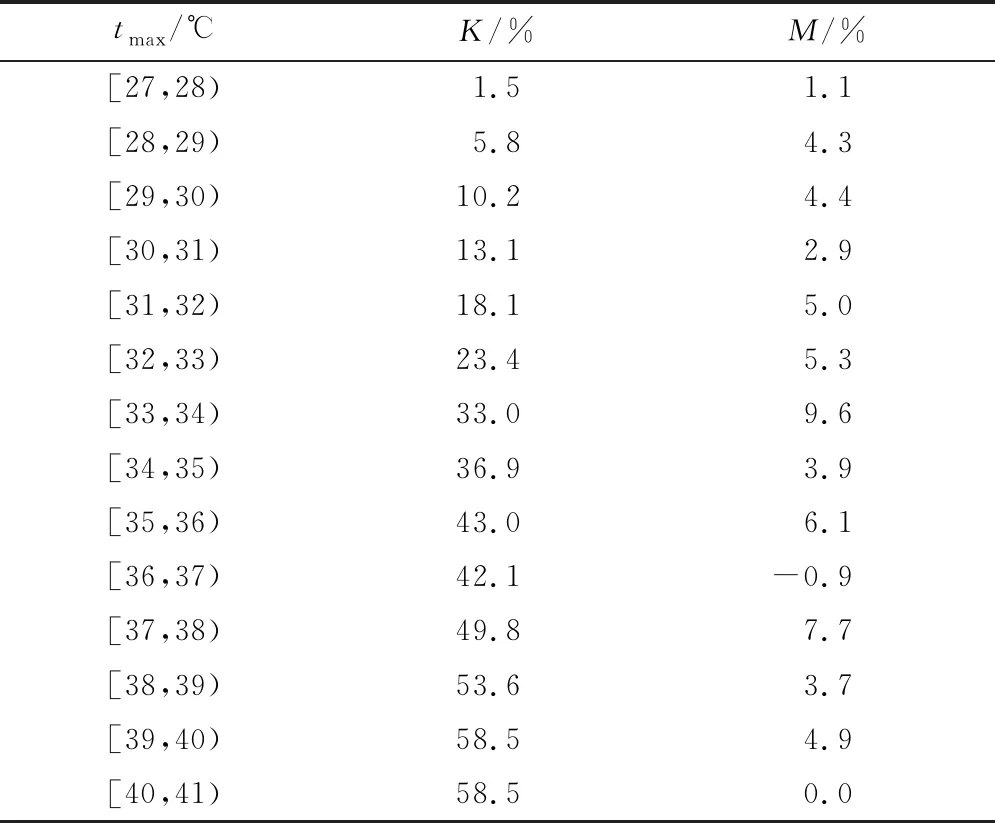
表1 上海2013-2017年日最高气温升高1 ℃时的日最大天气敏感负荷率平均值(K)及其增加值(M)

2.2.2 天气敏感负荷率与炎热累积效应指数的拟合

确定炎热累积效应对应的气温临界值后，根据公式(1)计算得到夏季炎热累积效应指数，与日最大天气敏感负荷率进行拟合分析,结果如图3所示。根据散点图的分布形态，选择线性回归拟合。从图3可以看出，上海2013-2017年夏季工作日和双休日炎热累积效应指数与日最大天气敏感负荷率存在显著的正相关，两者之间的R2分别为0.81和0.71。

图3 上海2013-2017年夏季工作日(a)和双休日(b)天气敏感负荷率与炎热累积效应指数拟合图

2.3 夏季最大电力负荷预测模型的建立

2.3.1 逐步回归模型

分别计算各个建模因子与日最大天气敏感负荷率的相关系数(见表2)，回归建模时剔除了部分相关性较差的因子(见表3)。方案1的回归模型中入选因子为x1、x2、x3、x8、x9,可以解释91%的方差。方案2的回归模型中入选因子为x1、x3、x6、x9、x10、x12，可以解释97%的方差，且前一天日最大天气敏感负荷率和前一天日平均天气敏感负荷率的回归系数占据的比重最大。

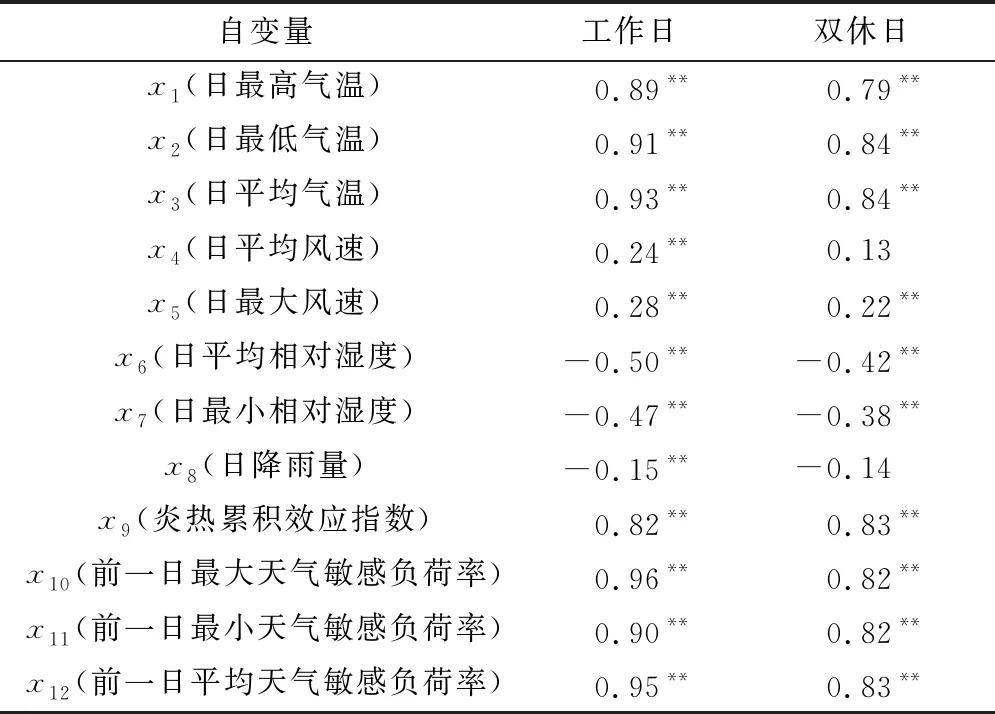
表2 上海2013-2017年夏季工作日和双休日日最大天气敏感负荷率与各建模因子的相关系数

表3 上海2017年夏季日最大电力负荷逐步回归预测模型

通过2013-2016年的数据建立了逐步回归模型，利用2017年数据对回归模型进行了验证，结果如图4所示。由图4可看出，方案1和方案2都能较好地模拟出负荷变化趋势，且模拟值与实际值偏差较小，工作日方案1和方案2的均方根误差(RMSE)分别为7.4%和6.3%，平均相对误差分别为4.5%和3.8%(见表4)。在6月和7月中旬回归模拟的结果与实际的天气敏感负荷率很接近，但当夏季出现极端负荷时，模拟值较实测值偏低，到了8月下旬以后模拟效果有所提升，此外回归方程很好地模拟了8月中旬负荷迅速下降的趋势。和工作日相比，双休日拟合的效果略差一些，这主要是由于双休日存在明显的假日效应。

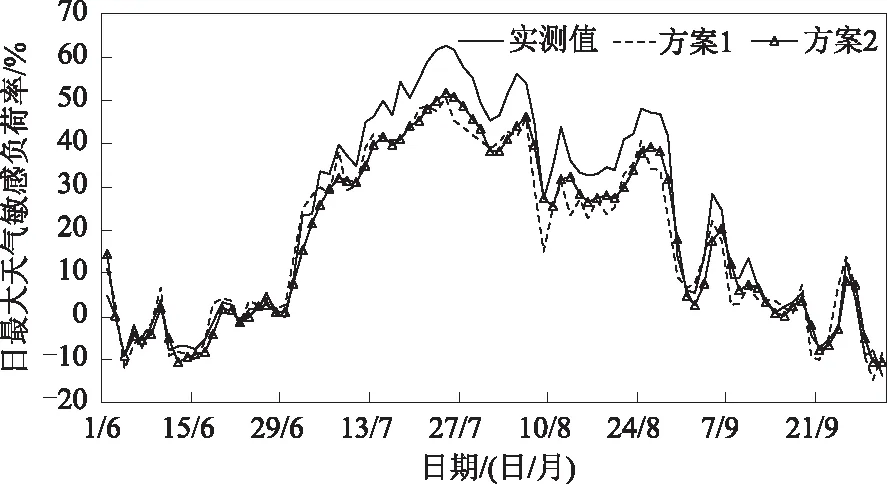
图4 上海2017年夏季工作日逐步回归模型的模拟值与实测值对比

2.3.2 SVR支持向量回归模型

由于SVR支持向量回归中已经将日期类型作为其中的特征变量，因此不用再区分工作日和双休日。采用2013-2016年的数据建立SVR支持向量回归模型，利用2017年的数据进行验证，模拟结果如图5所示。由图5可看出，模拟值与实测值变化趋势有很好的一致性，RMSE为4.5%(见表4)，平均相对误差为3.3%，尤其是对于夏季极端负荷的模拟表现出很高的吻合度。

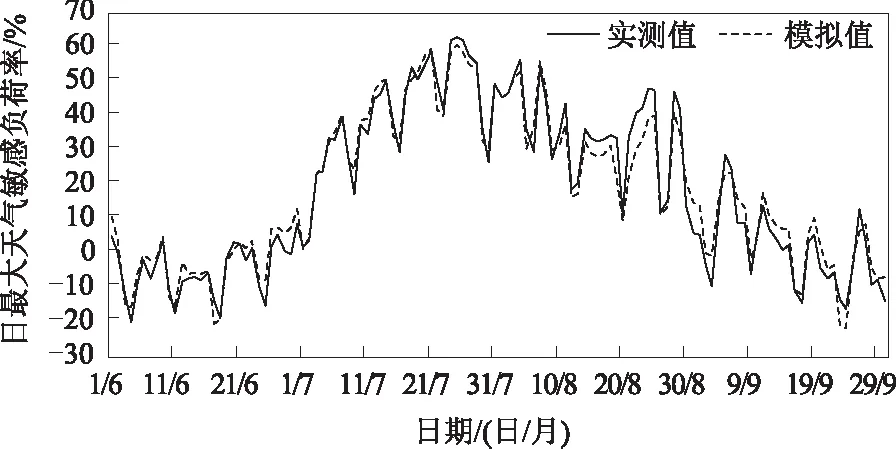
图5 上海2017年夏季SVR支持向量回归模型的模拟值与实测值对比

分析SVR模型模拟的相对误差与最高气温的关系发现(图6)，2017年7月11日-28日上海连续18天遭遇35 ℃以上的高温天气，用电负荷稳定在高位运行，SVR模拟的平均相对误差为1.9%，这也表明SVR支持向量回归模型可以很好地模拟上海夏季的极端负荷。但当气温低于30 ℃时，SVR模型模拟的用电负荷值往往较实际值偏高，尤其是当天气由炎热转为凉爽时，模拟值偏高较多。

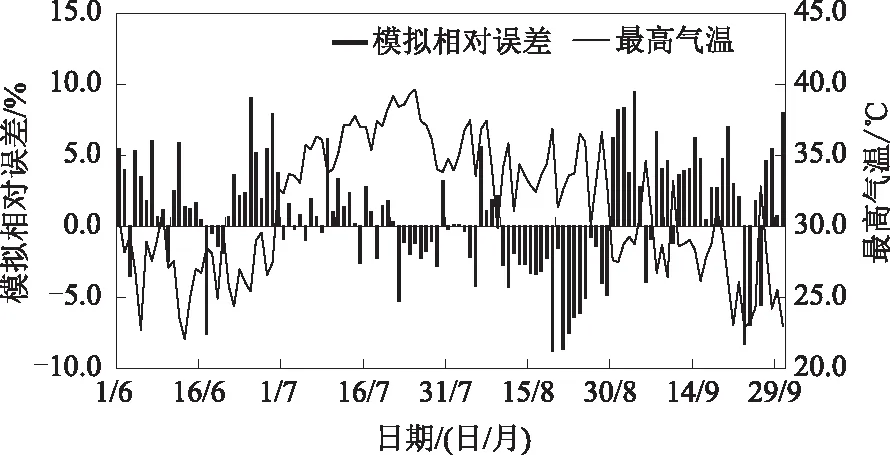
图6 上海2017年夏季工作日SVR支持向量回归模型的模拟相对误差与最高气温分布

2.3.3 两种回归预测模型的比较

不同模型的模拟误差见表4。由表4可知：SVR支持向量回归模型平均相对误差为3.3%，而逐步回归模型方案1和方案2的平均相对误差分别为4.5%和3.8%，总体来说SVR支持向量回归模型为最优。从相对误差小于2%和5%的日数占比来看，SVR的模拟效果最好，分别达38.2%和74.8%；逐步回归模型方案2的模拟效果次之，分别为25.8%和67.4%；逐步回归模型方案1的模拟效果相对最差，分别为22.5%和59.6%。从不同模型的最大相对误差可以看出：逐步回归模型方案2和SVR支持向量回归模型最大相对误差非常接近，分别为9.3%和9.4%；逐步回归模型方案1的最大相对误差达13.4%。

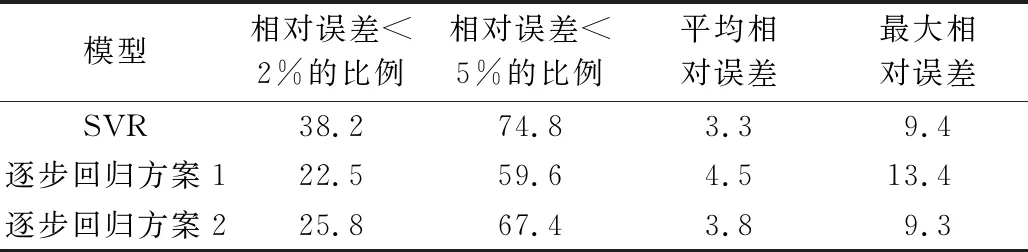
表4 上海2017年夏季不同的日最大电力负荷预测模型误差对比 %

逐月不同模型模拟的相对误差见表5。由表5可知：6月和9月两种逐步回归模型的模拟效果均优于SVR支持向量回归模型的模拟结果，SVR模型对于上海6月和9月负荷的模拟值较实测值偏高；但7月和8月的逐步回归模型模拟效果均明显差于SVR模型结果，表明SVR模型能很好地模拟上海夏季高温天气条件下的极端负荷，尤其是7月模拟的相对误差仅为1.8%。

表5 上海2017年夏季不同的日最大电力负荷预测模型逐月相对误差对比 %

3 结论与讨论

利用逐步回归和SVR支持向量回归两种方法分别构建上海市夏季逐日最大电力负荷预测模型，预测结果表明：加入前一天用电负荷数据作为自变量的逐步回归模型方案2较方案1(仅以气象要素作为自变量)的模拟效果有所提升，复相关系数由0.91上升到0.97，方案1和方案2的平均相对误差分别为4.5%和3.8%。SVR支持向量回归模型总体误差为3.3%，为三种模型中最优。

在模型分月预测效果分析中，6月和9月逐步回归模型的模拟效果较好，尤其是加入前一天用电负荷作为自变量的逐步回归模型方案2，模拟效果最优。7、8月SVR支持向量回归模型模拟效果最好，7月模拟的平均相对误差仅为1.8%，表明SVR回归模型能很好地模拟上海夏季的极端负荷。

采用SVR方法对上海夏季日最大电力负荷进行模拟时，模型对夏季极端负荷的预测模拟很好，但对6月和9月过渡时期的负荷模拟往往较实际负荷略偏高，今后有待进一步对模型算法进行调试和改进。建议今后在实际负荷预测业务中可以考虑采用两种模型的组合方式开展预测工作。

从两类模型的结果可以看出，机器学习SVR算法的效果好于逐步回归模型的效果，这是由多方面原因造成的。随着各地经济转型，高能耗的产业在逐渐减少，但数据中心等用电大户又在逐渐兴建，经济负荷并不是简单的线性增长；而且随着人们生活和消费习惯的改变，如电动车出行等因素的影响，这些行为一方面会引起用电负荷影响因子的增多，同时其对用电负荷的间接影响也在增大，即天气和用电负荷的关系趋于复杂，这可从SVR等机器学习算法能得到更好的效果中看到。