以制冷剂为工作介质的止推气体轴承静态特性分析*

滕 斌 杨启超 王 春 李连生

(青岛科技大学机电工程学院 山东青岛 266000)

离心式制冷系统的核心部件是离心式制冷压缩机，而离心式制冷压缩机的效率和可靠性是制约离心式制冷压缩机工作的关键因素[1]。在制冷工业的推动下 ，制冷压缩机的需求量急速增加。但近些年来，臭氧层破坏及温室效应等环境问题日益突出，压缩机制造商迫切需要研制出新技术，来提高产品的技术水平且保证新型制冷剂的环境友好性。目前采用磁悬浮的高速直驱的离心式制冷压缩机以及采用气浮轴承的离心式制冷压缩机是制冷压缩机行业的热点研究方向之一。随着高速电机和轴承技术的发展，磁悬浮轴承的离心式压缩机已经成功商业化，广泛应用于中央空调的冷水机组。磁悬浮轴承是一种随着高速电机而产生的高性能机电一体化产品，具有无需密封和润滑、噪声低、无机械磨损、寿命长等优点，但其控制复杂、成本高[2]。气浮轴承的气体介质黏度比液体黏度低很多，因此在高转速下产生的摩擦功耗和热量较低，制冷效率得到很大的提高，但其压缩性大，导致气浮轴承的承载力较低。因此有必要分析影响气体轴承承载力的参数，并通过优化设计来有效地提高气体轴承的承载力。

气浮动压轴承已经被成功应用于航空发动机等高速旋转机械，展现出了优越的性能。虞烈等人[3-4]给出了弹性箔片气体轴承的完全气弹润滑耦合解；GUO等[5]使用有限差分法建立了气体箔片轴承瞬态非线性承载力模型；杨利花等[6-7]通过实验方法进一步分析轴承承载力；刘良军[8]耦合黏温方程和热弹性变形方程，建立了气体推力轴承的热流体动力润滑方程；罗轶欣等[9-10]建立箔片动压气浮轴承的气热动试验台并进行了实验；闫佳佳等[11-12]建立气浮止推轴承的雷诺方程并进行静态、动态等理论分析。林韶宁等[13-14]对止推轴承的稳定性、轴向承载能力、启停性能等进行了大量试验；周权等人[15]采用有限差分法对动压气体止推轴承进行静态分析。从已知的文献可知，绝大多数研究针对采用空气为介质的气体轴承，主要对其静态特性、动态特性、理论及实验等方面进行了较为广泛的分析，而针对应用于制冷和热泵系统中的以制冷剂为介质的动压气体轴承特性研究较少。本文作者主要讨论转速、偏位角、轴承间隙对于以R134a和空气为介质的轴承承载力、摩擦力矩的影响，从而综合地对比分析以上2种介质下的轴承承载力、摩擦力矩。

动压气体在气膜间隙中的流动满足可压缩雷诺方程，通常采用数值方法求解雷诺方程,从而获得气体轴承的稳态特性。本文作者采用有限差分法和牛顿迭代法对雷诺方程进行数值计算，可以获得气膜压力分布，并计算出在制冷剂工作条件下的气体动压轴承的承载力，为制冷压缩机气体轴承工程设计及应用提供参考。

1 数学模型

1.1 建立雷诺方程

1.1.1 波箔片动压气体径向轴承的工作原理

如图1所示，在有外载荷情况下，转子表面会与平箔片之间产生一个楔形空间。当转子相对于平箔片旋转时，由于气体的黏性作用，使气体不断被带入到由大到小的楔形空间中，同时气膜被压缩而产生压力。膜压随着转速的增大而增大，直至转子和平箔片分离。

图1 波箔片动压气体径向轴承结构示意Fig 1 Schematic of dynamic gas bump foil journal bearing

1.1.2 稳态等温气体润滑雷诺方程

润滑气体在轴承间隙中的流动状态是动压气体轴承特征的决定性因素。从三维黏性Naver-Stokes方程入手，结合稳态气体连续性方程和状态方程，得到理想气体的等温稳态气体润滑雷诺方程：

(1)

其中，润滑气膜厚度h为

(2)

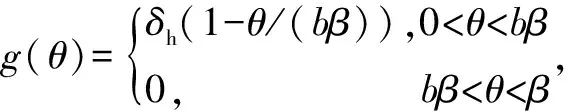
1.2 量纲一化

选取量纲一化参数，周围环境压力pa作为参考压力,最小初始气膜厚度h2，轴承外径R2为参考特征长度 ，则有:

可压缩流体的量纲一化定常Reynolds方程为

(3)

相应的量纲一化气膜厚度表达式为

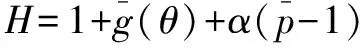
(4)

式中：Λ为轴承数，综合反映轴承运行条件和性能指标的物理量；α是波箔片等效线性弹簧的柔度。

1.3 数值计算

利用有限元差分对公式(3)进行离散化，从而得到最终的公式:

ai,jδi-1,j+bi,jδi+1,j+ci,jδi,j+di,jδi,j-1+ei,jδi,j+1=-Si,j

(5)

其中

2 计算对象与方法

2.1 计算对象

研究对象为在不同工作介质下的箔片轴承，基本参数参照文献[11]选取，具体参数如表 1所示。

表1 动压气体轴承相关参数

2.2 计算方法

采用有限差分法进行计算，计算过程主要分为以下几步:

(1)根据气体可压缩性和箔片变形，建立压力控制雷诺方程和气膜厚度方程；

(2)对雷诺偏微分方程进行有限差分处理；

(3)采用牛顿迭代法进行编程求解。

通过采用松弛法，进行迭代计算，压力计算流程图如图2所示，同时可将式(5)转换成下式：

图2 压力分布计算流程Fig 2 Flow of pressure distribution calculation

ω为迭代因子，收敛条件为

2.3 求解域网格划分

轴承内表面计算域网格划分如图3所示。

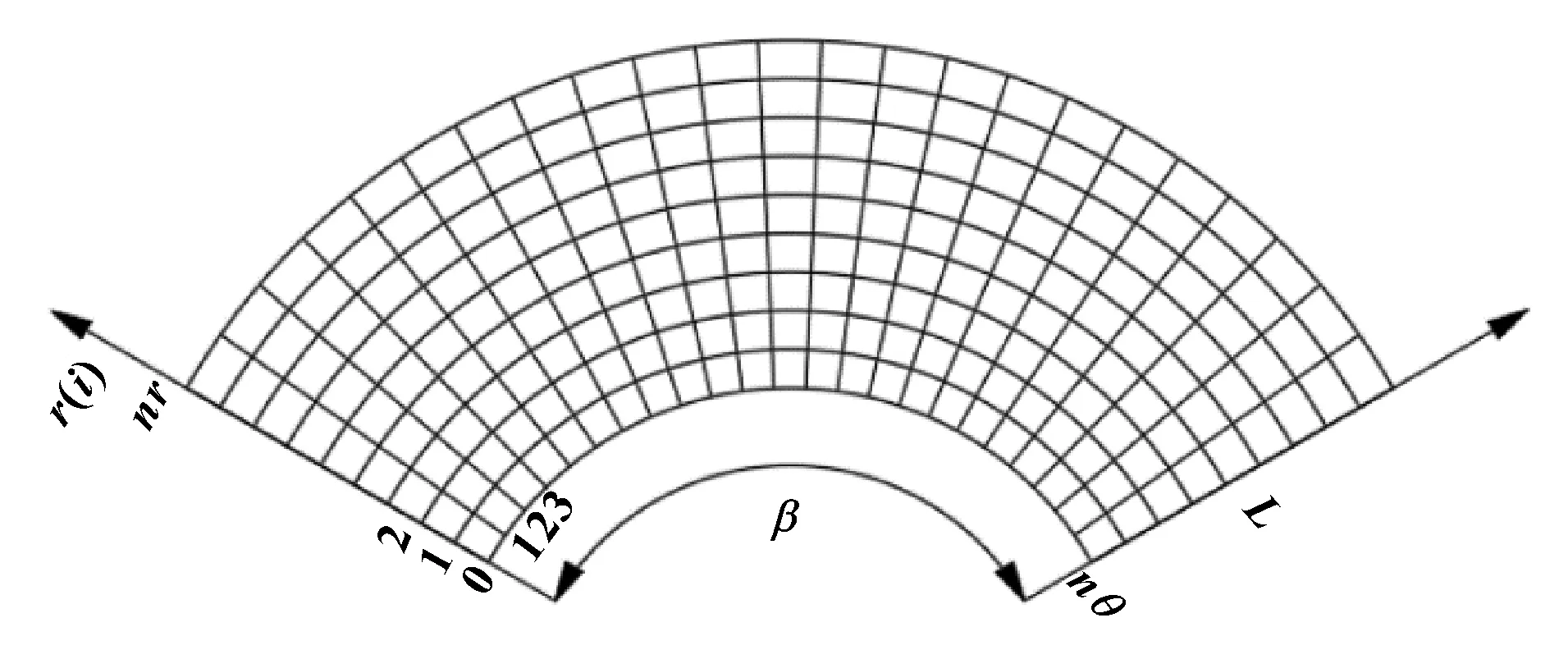
图3 计算域网格划分示意Fig 3 Schematic of grid division in the computing domain

2.4 边界条件及处理方式

压力边界条件:扇形瓦的每个边界都与外界环境相连，即这些部位的气膜压力等于周围工作气压。

2.5 验证分析

图4和图5所示分别为箔片轴承转速3×104r/min时得到的空气的气膜压力分布图、气膜厚度分布图,与文献[11]中的三维图吻合度很高，说明文中的计算方法是可行的。

图4 空气为介质时轴承量纲一气膜压力分布Fig 4 Dimensionless gas film pressure distribution of thebearing with air as the working medium

图5 空气为介质时轴承量纲一气膜厚度分布Fig 5 Dimensionless gas film thickness distribution of thebearing with air as the working medium

3 数值结果及分析

利用建立的计算模型，借助编程求解得到采用R134a为介质，扇形瓦张角为90°、转速为3×104r/min时的气体轴承量纲一气膜压力分布图以及量纲一气膜厚度分布图，如图6和图7所示。图中气膜压力峰值出现在轴承轴向中截面45°左右。

图6 R134a为介质时轴承量纲一气膜压力分布Fig 6 Dimensionless gas film pressure distribution of thebearing with R134a as the working medium

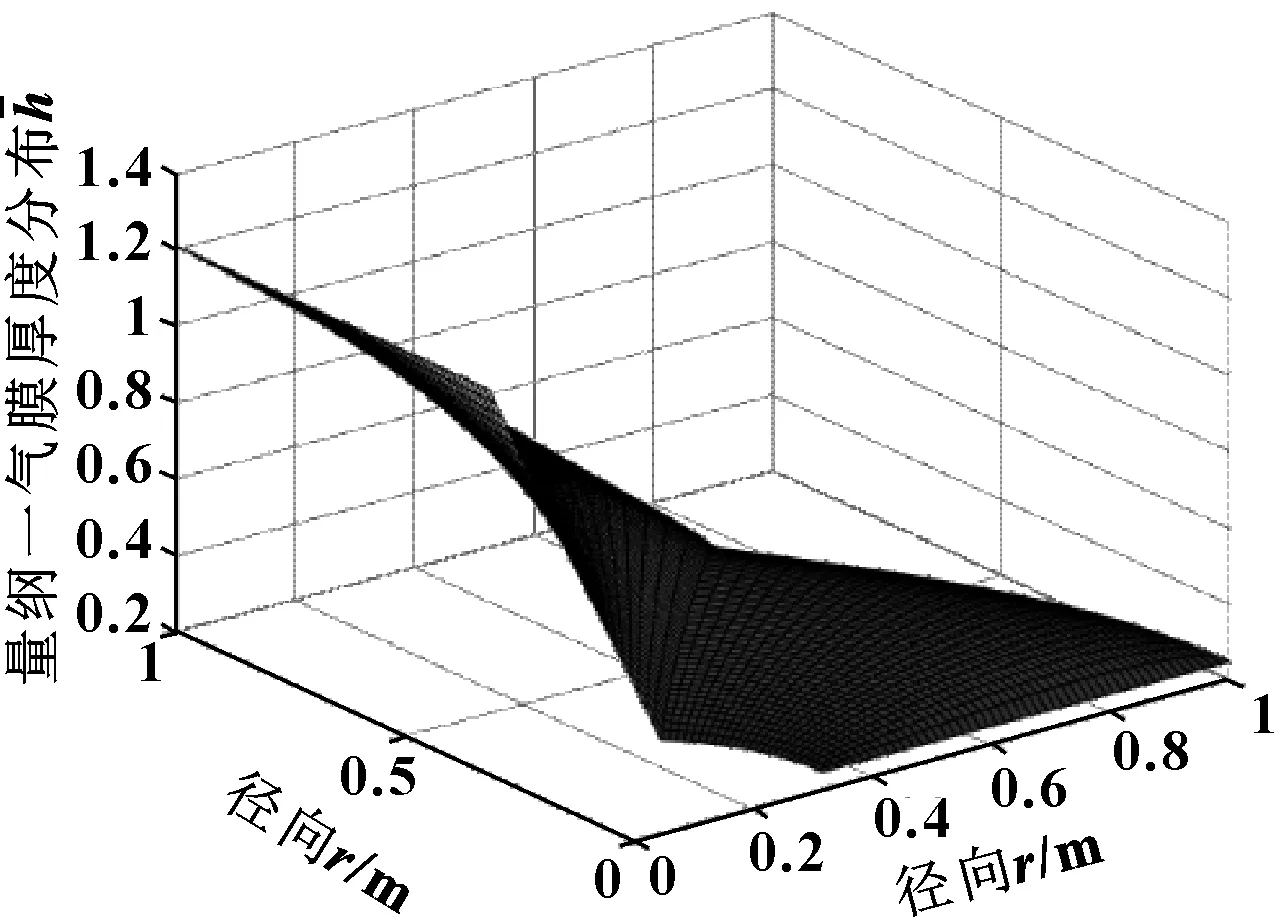
图7 R134a为介质时轴承量纲一气膜厚度分布Fig 7 Dimensionless gas film thickness distribution of thebearing with R134a as the working medium

为了分析承载力、摩擦力矩影响因素，逐一改变扇形瓦张角、节距比、倾斜面高度、最小初始气膜厚度等参数，同时比较制冷剂R134a与空气2种工质的不同，计算分析其对止推轴承承载力、摩擦力矩的影响。

3.1 扇形瓦张角对承载力、摩擦力矩的影响

通过改变扇形瓦张角的大小，得到在R134a与空气2种不同工质下轴承承载力、摩擦力矩与扇形瓦张角、转速之间的关系，如图 8、9所示。

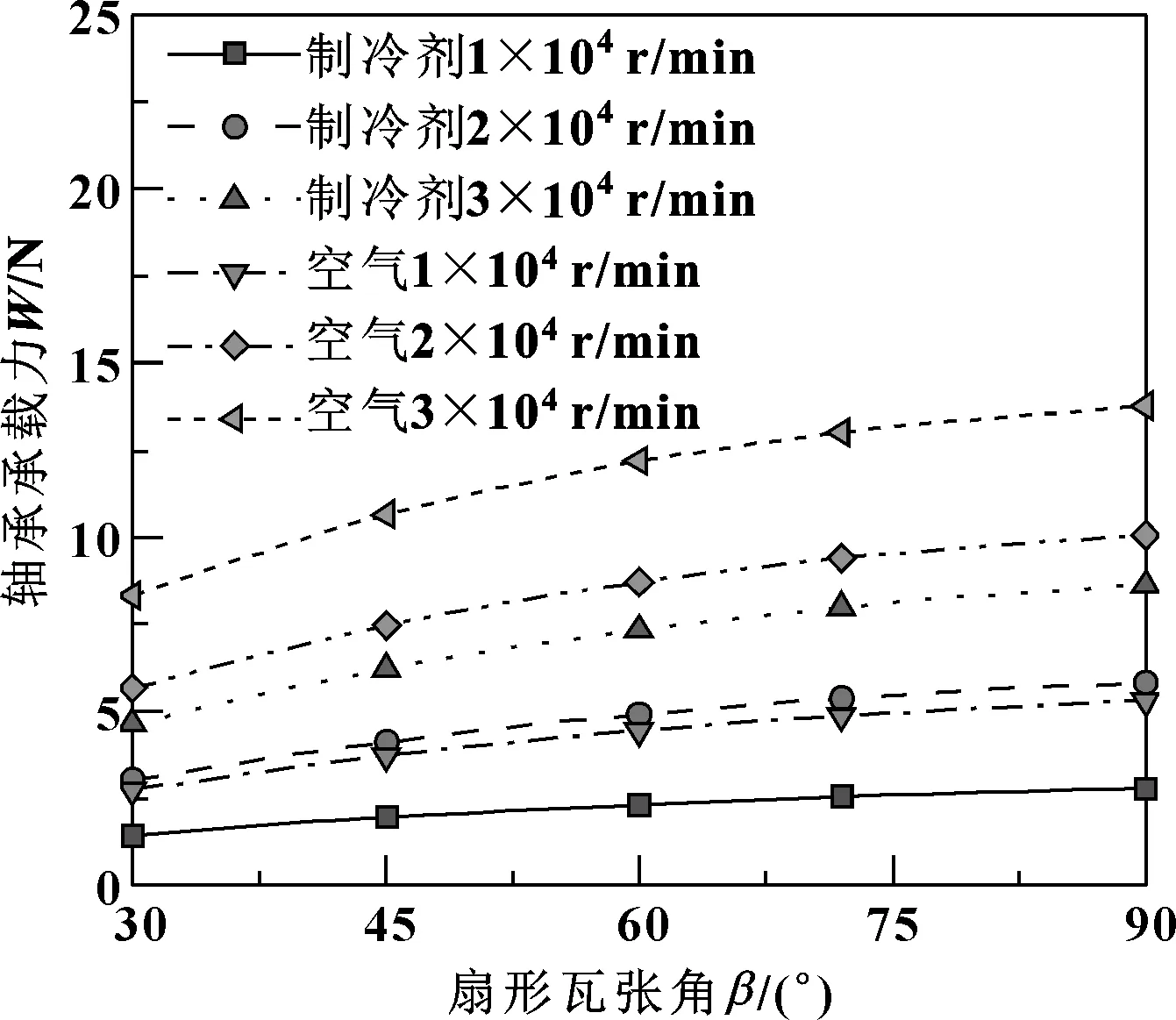
图8 不同速度下承载力与扇形瓦张角的关系Fig 8 The relationship between the bearing capacity and theopening angle of the fan-shaped tile at different speeds

对比发现，在扇形瓦张角不变的情况下，以R134a和空气为介质的轴承承载力和摩擦力矩都随转速的增大而增大；在转速不变的情况下，随着扇形瓦张角增大，两者的承载力也越大，而两者的摩擦力矩随扇形瓦张角的增大而减小。这是因为承载力的大小主要跟气膜压力与环境压力之差有关，摩擦力矩与气膜压力梯度有关。随着扇形瓦张角的增大，气膜峰值变化较小，但气膜压力分布更加平缓，承载力为气膜压力分布与环境压力之差的积分，由积分定义可得承载力随着扇形瓦张角的增大而增大，而由梯度定义可得摩擦力矩随着扇形瓦张角的增大而减小。同时，相同的扇形瓦张角和转速下，R134a的承载力是空气的52%～63%，而且两者承载力之比随转速的增大和扇形瓦张角的增大都会增大；R134a的摩擦力矩是空气的59%～63%，且两者摩擦力矩之比随转速的增大和扇形瓦张角的增大都会增大。这也是在轴承设计中应该关注的，工作载荷的大小决定了扇形瓦张角的大小，因此为确保轴承具有足够的承载力，在设计R134a气体轴承时要比空气气体轴承的扇形瓦张角偏大。

图9 不同速度下摩擦力矩与扇形瓦张角的关系Fig 9 The relationship between the friction torque and the openingangle of the fan-shaped tile at different speeds

3.2 节距比对承载力、摩擦力矩的影响

通过改变节距比的大小，得到在R134a与空气2种不同工质下轴承承载力、摩擦力矩与节距比、转速之间的关系，如图10、11所示。

由图10、11可得，在转速不变的情况下，以R134a和空气为介质的轴承承载力随节距比的增大而先增大后减小；转速1×104r/min的情况下，在节距比取0.6时，两者承载力达到最大值，但随着转速的增大，两者的承载力的峰值向左偏移(节距比减小方向)。同时，相同的节距比和转速下，R134a的承载力是空气的42%～67%，而且两者承载力之比随节距比的增大而增大。同时可以得到，在转速不变的情况下，以R134a和空气为介质的轴承摩擦力矩随节距比的增大而减小。同时，相同的节距比和转速下，R134a的摩擦力矩是空气的59%～63%，而且两者承载力之比随节距比的增大而减小。

图10 不同速度下承载力与节距比的关系Fig 10 Relationship between bearing capacity andpitch ratio at different speeds

图11 不同速度下摩擦力矩与节距比的关系Fig 11 Relationship between friction torque and pitchratio at different speeds

3.3 倾斜面高度对承载力、摩擦力矩的影响

通过改变倾斜面高度的大小，得到在R134a与空气2种不同工质下轴承承载力、摩擦力矩与倾斜面高度、转速之间的关系，如图 12、13所示。

从图12、13可以看出，在转速不变的情况下，以R134a和空气为介质的轴承承载力随倾斜面高度的增大而先增大后减小，当倾斜面高度为18 μm，承载力到达峰值；以R134a和空气为介质的轴承摩擦力矩随倾斜面高度的增大而减小。上述现象的原因是顶箔是由一个水平平面和一个倾斜平面构成，与转子表面形成楔形收敛间隙，因此膜厚比(倾斜面高度/最小气膜厚度)对动压效应的形成有非常大的影响。由于楔形效应，承载力先随着膜厚比的增大而增大，但当膜厚比过大，润滑气体有可能难以通过狭窄的气膜间隙而发生回流。这种气体回流现象降低了承载力。摩擦力矩主要来源于库埃特流摩擦损耗，随着膜厚比的增大，止推轴承收敛间隙的库埃特流摩擦损耗快速降低，摩擦力矩减小[8]。同时，相同的倾斜面高度和转速下，R134a的承载力是空气的47%～67%，而且两者承载力之比随倾斜面高度的增大而减小。同时，相同的倾斜面高度和转速下，R134a的承载力是摩擦力矩的59%～61%，而且两者承载力之比随倾斜面高度的增大而减小。

图12 不同速度下承载力与倾斜面高度的关系Fig 12 Relationship between bearing capacity and height ofinclined surface at different speeds

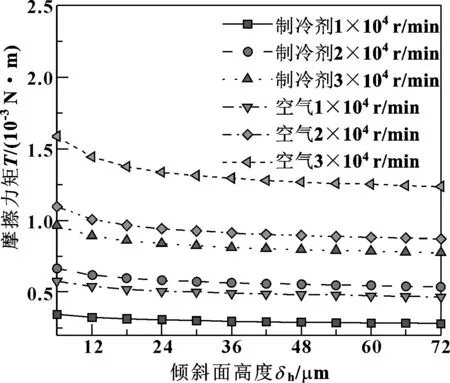
图13 不同速度下摩擦力矩与倾斜面高度的关系Fig 13 Relationship between friction torque and height ofinclined surface at different speeds

3.4 最小初始气膜厚度对承载力、摩擦力矩的影响

轴承间隙的数值在几微米至十多微米之间，因此细微的差别都会使得动压气体轴承特性产生较大的变化。

从图14、15可以看出，在转速不变的情况下，以R134a和空气为介质的轴承承载力、摩擦力矩都随最小初始气膜厚度的增大而减小。同时，相同的最小初始气膜厚度和转速下，R134a的承载力是空气的50%～72%，R134a的摩擦力矩是空气的58%～64%，而且两者承载力和摩擦力矩之比随最小初始气膜厚度的增大而减小。

图14 不同速度下承载力与最小初始气膜厚度的关系Fig 14 Relationship between bearing capacity and minimuminitial film thickness at different speeds

图15 不同速度下摩擦力矩与最小初始气膜厚度的关系Fig 15 Relationship between friction torque and minimum initialfilm thickness at different speeds

4 结论

针对R134a和空气为润滑工质的止推气浮轴承，采用数值分析的方法研究了几何条件、转速以及润滑工质的变化对径向气浮轴承的承载力、摩擦力矩等特性的影响，得到了如下结论：

(1) 扇形瓦张角、节距比、倾斜面高度、最小初始气膜厚度均对R134a和空气为工质的气体轴承承载力有影响，其中最小初始气膜厚度的影响最大，扇形瓦张角越大、转速越高、最小初始气膜厚度越小，以两者为介质的轴承承载力越大;相同转速下以两者为介质的轴承承载力随倾斜面高度和节距比的增大而先增大后减小;但相同的情况下R134a的承载力要低于空气的承载力，所以在设计以R134a为工质的气浮轴承时，偏心率和轴承间隙都要偏大。

(2) 扇形瓦张角、节距比、倾斜面高度、最小初始气膜厚度均对R134a和空气为工质的气体轴承摩擦力矩有影响，其中最小初始气膜厚度的影响最大，扇形瓦张角和节距比影响很小，转速越高、最小初始气膜厚度越小，以两者为介质的功率损耗越大;但相同的情况下R134a为介质时的摩擦力矩要低于空气为介质时。

(3)研究表明在设计以R134a为工质的气浮轴承时，取较大的扇形瓦张角、节距比取0.5、取合适的倾斜面高度、取较小的最小初始气膜厚度，可以获得较高的承载力，同时系统功率损耗低。