从细节入手，助推学生解决问题的能力提升

摘 要：一些学生在解决实际问题的时候感觉到困难，成功率不高，其原因是多方面的。比如说理解问题的能力不够，缺乏相应的数学模型，以及学生缺少分析问题的方法和习惯等。实际教学中教师要关注学生解决问题遭遇障碍的细节，对症下药，帮助学生从读懂问题开始，到建立思路，掌握基本的分析问题方法，形成数学模型，再到养成检验的良好习惯，从而提升学生解决实际问题的成功率，让学生在学习过程中进一步提升数学能力。

关键词：审题;分析问题;数学模型

中图分类号：G623.5

文献标识码：A

文章编号：2095-624X（2021）03-0059-02

有些学生特别害怕解决实际问题这样的题型，往往遭遇这样的问题就手足无措，草率列式计算，结果导致错误率极高。究其原因，学生的数学理解力差、缺乏科学的读题习惯，分析问题的能力欠缺以及缺少对应的数学模型是主因。针对学生的这些困难，在实际教学中教师可以从学生解决问题的各个环节入手，聚焦学生的做题细节，给他们一些必要的指引。

一、关注审题细节，让学生先读懂问题

审题是解决实际问题的先决条件，只有在读懂问题的基础上，才能综合条件和问题去达成两者间的联系，从而顺利地解决问题。但是在教学中我们发现一些学生在审题环节十分马虎，有些学生根本不去细读题目，而是浮光掠影。实际教学中教师要关注学生的审题细节，要想办法让学生体会到审题的重要性，从而加强学生的审题，让学生在理解題意的基础上去展开分析，为学生成功解决问题奠定基础。

学生不注重审题或者审题的效果较差有两种原因。一种是能力问题，学生可能阅读理解的能力较差，不怎么能读懂题目。针对这些学生，教师要教给学生一些简单的读题技巧，让学生一边读题一边圈画出题中的关键条件，多经历和多尝试之后，学生就能够轻松应对一些基本的题型了。另一种可能是学生的审题习惯较差，他们在快速读题的时候已经调用了之前的经验，将问题臆想成之前已经遇到的问题。针对这样的情况，教师要有意引导学生去感悟读题的重要性。举个简单的例子：南通和北京相距1000千米，一辆车以每小时80千米的速度从南通开往北京，5小时之后汽车离南通多少千米？学生在独立尝试并解答之后，教师可以挑选一些不同学生的解答过程来展示，学生很快会发现两者的思路不同，一种是计算汽车已经行驶的路程，一种是计算汽车还要行驶的路程。那么回过头再来读题，可以发现题中的问题是“汽车离南通的路程”，也就是汽车已经行驶的路程。这是一个简单的实际问题，为什么很多学生犯了错？原因就在于学生的“自以为”。他们根本没有审题，只是习惯性地求出汽车离北京的路程，其实学生的潜意识中是这样想的：如果是求汽车已经行驶的路程，那么南通到北京的路程根本不需要，所以这个问题一定是求汽车还要行驶多少路程。引导学生再次读题审题之后，学生会发现自己犯的错是多么可笑，这也会增强学生认真读题审题的意识，推动学生良好的解题习惯的养成。

二、关注分析细节，让学生掌握基本方法

有些学生在解决问题的时候不是综合条件去分析可以求出什么问题，或者从问题出发去思考需要找到哪些条件，而是根据自己的经验来做。他们在遇到现实的问题时总是去回忆是不是已经遇到过这样的问题，这样的方法对于灵活多变的实际问题而言是落后的，不切实际的，所以在实际教学中教师要帮助学生形成解决问题的思路，要让他们掌握基本的分析问题的方法。

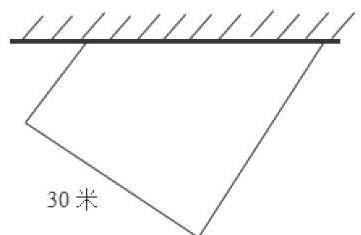
例如在教学“梯形的面积”时，出现了这样一个问题：如图，用70米长的栅栏靠墙围成一个直角梯形，梯形的高是30米，梯形的面积是多少平方米？一些学生在读题之后找不到地方入手，我在组织学生交流的时候，从问题入手引导学生去建立思路：①梯形的面积公式是什么？②要计算出梯形的面积，需要找到哪些条件？③到题中找一找，已经知道了什么条件，还要找到什么条件？在这些问题的引导下，学生发现要计算这个梯形的面积，先要找到梯形的上下底分别是多少米，而题中已经知道三条边的总长度，用70米减去高的30米可得梯形的上下底之和为40米。有了这样的分析，学生的思路就建立起来，问题迎刃而解。更加重要的是学生在这样的分析过程中还有另外的收获，就是不需要知道梯形的上底和下底分别是多少，只要找到两者的和就可以，这让学生形成了整体的数学思想。

在这个教学案例中，学生分析问题既从问题出发去寻找条件，又在遭遇阻碍的时候尝试从条件出发去思考可以求出什么问题，这样综合两种不同思路，学生顺利解决了问题，而且经历了这样的思路构建，学生可以自己去尝试从不同的途径来分析问题，为他们在解决实际问题时能够成功找到思路助力。

三、关注探索细节，让学生弄懂问题

数学教学中要真正培养学生解决问题的能力，而不是让学生在大量的重复练习中形成固有的解题模式，为此教师要关注学生在解决问题过程中出现的一些细微的差错，找到他们出现错误的原因，然后对症下药，想办法引导学生从根本上去弄懂问题，从知道“怎样做”走向知道“为什么要这样做”，以此提升学生解决实际问题的能力。

例如在“三角形的面积”教学中有这样的问题：一块三角形的田地，底边长60米，高40米，如果每平方米种植8棵番茄，一共可种植多少棵？笔者在批改学生作业的时候发现除了三角形的面积忘记了除以2之外，这个问题错误的原因集中在算出三角形的面积之后用除法来计算番茄的棵数上。为什么会出现这样的错误呢？从错误的比例来看这不是一种偶然，于是我重新审视这个问题，发现这个问题与之前学生做过的一个练习比较相似：一个三角形的梨园，底边长40米，高是20米，如果每棵梨树占地8平方米，那么梨园一共可种植梨树多少棵？对比这两个问题可以发现，学生在解题的时候犯了“经验主义”的错误，他们没有去推敲如何算出番茄的棵数和梨树的棵数，而是根据经验来用除法计算，所以讲解这道习题的时候，我将两个问题拿来做对比，引导学生从“每棵梨树占地8平方米”和“每平方米种植8棵番茄”来做对比，让学生发现第一个问题是要看总面积中有几个8，而第二个问题是要求出1200个8是多少。经过对比之后，学生对这两个问题模型就清晰了，再遇到类似的问题，学生一定可以从算理出发去列式计算，避免之前的错误。

从这个例子可以看出，学生解决问题的关键在于弄懂问题，而不是大量重复的机械练习，所以教师需要着重于学生的理解来教，需要通过典型例题的讲解、对比来为学生构建清晰的模型，这样学生在遇到类似问题的时候就可以调用此知识经验来解决问题，从而提升他们解决问题的能力。

四、关注理解细节，让学生构建数学模型

数学建模是数学学习中一个重要的环节，也是提升学生解决问题能力的关键所在。教学中教师要提供给学生一类问题，学生经过比较发现问题的共性，建构初步的数学模型，然后在不断遭遇新的问题时再去拓展数学模型，累积解决这类问题的经验，让解题的思路自动化，以此提升学生解决实际问题的能力。

例如在“假设的策略”教学中，我设计了这样一个问题：将720毫升的果汁倒入一大六小共计7个杯子，正好倒满，已知1个大杯子的容量和3个小杯子的容量相等，那么大杯子和小杯子各装多少毫升果汁？学生在读题之后很快发现可以利用大杯子和小杯子的容量關系，将大杯子换算成小杯子或者将小杯子换算成大杯子来计算。之后我又出示了几道类似的问题，比如用大箱子和小箱子装球的问题，师傅和徒弟一起加工零件的问题，学生都顺利地解决了问题。后来我引导学生比较和小结，学生发现几个问题的共性都是利用两种未知量之间的关系，将其中一个假设成另一个来计算，因为题中的未知量都是倍数关系，所以在假设替换的时候，总量是不变的，也就是被除数不变，而除数发生了变化。这样的认识不仅建构了这类问题的模型，让学生一接触此类问题就想到怎样来将两个未知数转化成一个，而且为接下来教学一个量比另一个量多（少）的多少关系中的假设问题奠定了基础。

五、关注检验细节，让学生养成良好习惯

在解决问题教学时，要求学生检验是比较重要的，因为在检验的过程中，学生可以重新理一理思路，可以站在不同的角度去审视解决问题的过程，所以在检验中可以发现之前做题时的一些小失误。而一旦学生享受到检验的“红利”，他们会更加注重检验，会逐渐形成检验的良好习惯。

例如这样一个问题：学校机器人社团原有女生12人，占总人数的40%，现在要将女生人数提升到总人数的50%，需要再加入多少名女生？很多学生在解决这个问题的时候，用女生的人数除以百分数得到社团的总人数是30人，然后用总人数乘50%得到15人，再用15减12得到3人。这个思路显然是有问题的，因为只要稍加检验就可以发现，随着女生人数增加3人，总人数变成33人，那么女生的人数不可能是总人数的一半。所以通过检验可以发现之前的思路是错误的，学生在做题的时候应该要抓住人数不变的男生来做，根据女生人数和女生的占比可以求出机器人社团的总人数，用总人数减去女生人数可以得到男生人数为18人，增加一些女生后女生人数要达到50%，所以只要用男生人数减去女生人数即可，得到增加的女生为6人，这个数据再代入原来的问题去检验就毫无问题。

要求学生检验不是简单的走过场，不应该只体现在形式上，而是要敦促学生实实在在地去检验。可以从不同角度去思考和审视问题，需要在思路、算理和具体的计算上都进行仔细的检验，这样可以充分发挥检验的实效，帮助学生提升解决问题的能力。

总之，解决问题是学生数学学习必然面对的重要问题之一，也是学生将所学数学知识应用到实际问题中，增强学生学以致用能力的重要途径，在实际教学中教师要关注学生解决问题的困难，要从细节入手来对症下药，切实提升学生解决问题的能力。

[参考文献]

[1]成琳琳.关注细节 提升学生解决实际问题的能力[J].名师在线，2018（8）：65-66.

[2]张 铭.“对症下药”——有效提高学生解决问题的能力——小学数学解决实际问题教学中存在的问题及应对策略[J].华夏教师. 2015（S1）：63.

作者简介：胡晓兵（1977— ），男，江苏如皋人，  中小学一级教师，本科，教研组长，研究方向：小学数学教学。