基于材料参数更新的RC框架结构时变易损性分析*
2021-08-26杨思昭王宪杰
杨思昭,王宪杰,2
(1 云南大学建筑与规划学院,昆明 650500;2 浙江大学建筑工程学院,杭州 310058)
0 概述
地震易损性分析能够预测在不同强度地震作用下,建筑结构达到或超越不同性能水准的概率[1-2]。但传统的易损性分析主要是静态的,未考虑材料性能衰退对结构抗震性能的影响。事实上,结构在全寿命周期内,随着服役龄期的增加,由于受力构件有效截面面积的减小和材料力学性能的退化,结构在同一地面运动加速度作用下发生破坏的概率增加[3-4]。因此,在进行地震易损性评估的研究中,考虑材料时变特性的影响更能真实反映不同服役期建筑结构的地震易损性。
但由于耐久性研究存在时间跨度长、影响因素复杂、不确定性大等问题,目前尚未有统一、可靠的理论模型来刻画材料、构件和结构层面的长周期、随机衰变特性。与此同时,在实际工程的检测、监测和检修等作业中,已取得了服役结构的诸多性能参数。但实际工程中的实测数据(特别是有损检测)由于样本数量少而缺乏足够的代表性,仅依靠小样本检测数据评估建筑结构的实际工作性能缺乏足够的完备性[5]。结合现有的实测数据,引入信息更新理论对初始设计模型不断修正和完善,可实现对具体结构性能退化的合理预测。针对实时信息更新与系统吸收,经典贝叶斯方法可以有效实现对先验分布的相关参数进行重新估计和检验,得到系统后验分布数据[6-7]。因此,采用贝叶斯方法进行结构耐久性分析既能利用多年来耐久性基础研究对结构内在规律的理性认识,又能考虑结构的实际情况[8],从而准确刻化结构实时动态性能。
退化结构的时变结构抗力是非平稳随机过程,要求必须以随机过程理论为基础,研究随机荷载效应超过随机抗力的概率[9]。即通过理论分析研究结构的时变易损性时,同时需要考虑结构自身参数的不确定性和外界激励的随机性。此外,在传统的地震易损性研究中,为了便于问题的求解,通常需要基于以下几点假定进行分析[2-4,10]:结构地震需求参数和给定地震动水平作用之间服从幂指数回归关系;在给定地震动水平作用下,结构地震需求参数服从对数正态分布;结构的概率抗震能力服从对数正态分布。显然,基于此求解得到的地震易损性结果只是经验估计值,不能反映结构响应的真实概率分布。李杰[11]提出的概率密度演化理论不仅为复合随机问题的求解提供了理论依据,而且可以分析得到满足真实分布的结构响应概率密度分布函数,为精细化评估既有结构的地震易损性提供了新思路。
本文通过总结建筑材料耐久性的相关研究成果,建立材料力学性能退化模型;引入不同服役龄期材料力学性能的实测数据,并采用贝叶斯方法进行数据更新。基于更新的材料性能退化模型与概率密度演化理论对某7层带内廊式对称三跨RC框架结构的地震易损性进行分析,得到RC框架结构抗震性能随服役龄期的一般变化规律。
1 材料性能时变特性分析与贝叶斯方法
1.1 随机参数更新贝叶斯方法
已有研究[12-13]表明,一般大气环境中既有建筑物混凝土的抗压强度服从正态分布,其均值和标准差是服役时间t的函数。采用共轭先验分布确定均值μ的后验分布。当方差σ2已知时,均值μ的先验分布可视为服从正态分布N(θ,τ2),即:
(1)
式中:θ,τ为超参数,可根据先验预测公式进行确定。
先验分布反映对研究对象内在规律的理性认识,不可避免的存在主观判断,尚需考虑其实际情况。设t时刻材料物理性能参数的实测样本值{x1,x2,x3,…,xn}取自总体样本N(μ,σ2),其中方差σ2已知。则此样本x的似然函数可表示为:
(2)
进而,由贝叶斯方法可将结构物理参数μ的后验分布表示为:
(3)
将式(1),(2)带入式(3),经过一定的数学推导可得μ的后验分布为:
(4)


(5)
图1给出了采用贝叶斯方法对材料性能参数进行信息更新的一般流程。

图1 材料性能参数贝叶斯动态信息更新过程
1.2 混凝土经时抗压强度预测模型
一般而言,混凝土经时抗压强度的均值在初期随时间增大而增大,但增长速率逐渐减缓,在后期则随时间增大而降低;标准差随时间增大而增大,且不受均值影响。牛荻涛等[12]通过分析长期暴露试验和实测的服役混凝土强度,建立了一般大气环境中混凝土强度均值μf(t)和标准差σf(t)的经时变换模型:
μf(t)=1.452 9exp[-0.024 6(lnt-
1.715 4)2]·μ′0
(6)
σf(t)=(0.030 5t+1.236 8)·σ′0
(7)
式中μ′0和σ′0分别为混凝土28d强度均值和标准差。
本文依据《混凝土结构设计规范》(GB 50010—2010)给出的混凝土抗压强度均值和标准值之间的关系,将混凝土强度均值μf(t)的经时变化模型转换为混凝土强度标准值fcu(t)的经时变化模型:
fcu(t)=μf(t)-1.645σf(t)
(8)
1.3 钢筋材料性能时变模型
相较于混凝土经时抗压强度的研究,钢筋经时锈蚀深度已有较为成熟的研究成果[14],且已在规范中进行体现[15]。处于一般大气环境中的RC框架结构,钢筋锈蚀开始时间ti可按下式进行计算:
(9)
式中:C为混凝土保护层厚度;k为碳化系数;x0为碳化残量。具体参数取值详见规范[15]。
钢筋锈蚀是一个电化学腐蚀过程,其锈蚀速率与钢筋表面的含氧量有关,而含氧量取决于混凝土质量、保护层厚度和环境条件。在温度为20℃,相对湿度为75%的典型环境中,钢筋初始锈蚀电流密度icoor(1)为[14]:
(10)
式中w/c为水灰比,当已知混凝土抗压强度标准值fcu(t)时,水灰比可按下式计算:
(11)
进而,钢筋开始锈蚀之后的某时刻tc,钢筋锈蚀电流密度icoor(tc)为:
(12)
通常情况下,当锈蚀电流密度icoor为1μA/cm2时,相应的钢筋锈蚀深度速率为11.6μm/年。
2 经时材料本构关系定义
2.1 经时混凝土的本构关系
相较于大量已有的时不变或素混凝土本构关系模型,考虑锈蚀箍筋约束影响建立的经时混凝土本构关系更符合实际服役情况。在考虑了体积配箍率、箍筋屈服强度等影响因素建立的Kent-Scott-Park模型基础上,通过引入峰值应力和应变软化修正系数[16]建立了锈蚀矩形箍筋约束混凝土本构关系模型,如式(13)所示:
(13)
式中:σc和εc分别为锈蚀箍筋约束混凝土的应力和应变;εcc为锈蚀箍筋约束混凝土的峰值点应变,εcc=0.002c2K;εcu为锈蚀箍筋约束混凝土的极限应变;c1,c2和c3分别为非锈蚀箍筋约束混凝土的峰值应力、峰值点应变和应变软化调整系数,按式(14)确定;k1,k2分别为考虑箍筋锈蚀影响的峰值应力和应变软化修正系数,按式(15)确定;K为考虑箍筋约束影响的混凝土强度增强系数,按式(16)确定;Zm为应变软化段斜率,按式(17)确定;fc(t)为混凝土的轴心抗压强度。
c1=0.157 0λt+0.963 4
(14-1)
c2=-1.556 8λt+1.232 0
(14-2)
c3=17.744 0λt+0.974 2
(14-3)
k1=(0.291 4λt-0.179 1)ω+1.0
(15-1)
k2=exp[(-1.585 2λt+0.960 8)ω]
(15-2)
(16)
(17)
式中:λt为箍筋特征值;ω为锈胀裂缝宽度;ρs为体积配箍率;fyh为箍筋屈服强度;h″为从箍筋外边缘算起的核心混凝土宽度;sh为箍筋间距。
2.2 锈蚀钢筋的本构关系
实际工程中的锈蚀钢筋,当其锈蚀率ηs<80%时,本构关系可按式(18)进行确定[17]:
(18)
式中:σs和εs分别为锈蚀钢筋的应力和应变;Es0为未锈蚀钢筋的弹性模量;fyc,fuc分别为锈蚀钢筋的屈服强度和极限强度,按式(19)确定;εsyc,εshc和εsuc分别为锈蚀钢筋的屈服应变、强化应变和极限应变,按式(20)确定。
(19-1)
(19-2)
(20-1)
(20-2)
εsuc=e-2.501ηsεsu0
(20-3)
式中:fy0,fu0分别为未锈蚀钢筋的屈服强度和极限强度;εsh0,εsu0分别为未锈蚀钢筋的强化应变和极限应变;ηs,cr为钢筋屈服平台消失时的临界锈蚀率,带肋钢筋取20%,光圆钢筋取10%。
3 基于PDEM的结构时变易损性分析
时变易损性表征既有建筑结构在不同服役时期遭遇可能强度地震作用时,结构达到或超越各级性能水准的概率。可表示为:
FR(a,t)=Pf[PL|SA=a,T=t]
(21)
式中:FR(a,t)为结构的时变易损性;Pf为失效概率;PL为结构的性能水平;SA为地震动强度指标,SA=a;T为结构服役期,T=t。
显然,结构响应θ(SA,T)达到或超过目标性能水准θc的概率可表示为:
Pf[SA,T]=Pr[θc≤θ(SA,T)]
(22)
通过以上分析可知,划分合理可信的目标性能水准和较为精细化求解结构在不同地震动强度和不同服役年限条件下的结构响应是时变易损性分析的基础,以下分别就这两方面进行讨论。
3.1 概率抗震能力分析
《建筑抗震设计规范》(GB 50011—2010)蕴含丰富的基于性能抗震设计思想,其目标性能的选定依托于对性能水平的合理划分。针对RC框架结构,可采用结构层间位移角来定义结构的性能水平,将RC框架结构不同破坏程度对应的最大层间位移角限值列于表1。在此指出,为了便于问题的考虑,本文将各目标破坏状态限值视为确定量进行考虑。

破坏等级与最大层间位移角限值的关系 表1
3.2 基于PDEM的概率地震需求分析
传统的易损性分析方法通常假定概率地震需求参数服从对数正态分布,是基于经验的一种近似分析方法。区别于传统方法,基于概率守恒原理提出的概率密度演化理论[11,18]可以准确求取结构动力响应的概率密度函数及其演化过程,为结构的概率地震需求分析提供了新思路。
假设结构反应需求参数Z(t)为所考察的状态量,对于某一物理解答存在、唯一且连续依赖于初始条件的概率保守系统(Z(t),Ψ),其中Ψ=(Ψ1,Ψ2,…,Ψs)为随机参数向量,s为随机变量的个数,其联合概率密度函数为PZΨ(z,ψ,t),根据概率守恒原理的随机事件描述,则有:
(23)
式中:D/Dt(·)为全导数;Ωt×ΩΨ为初始状态空间在t时刻对应的解区域,对其经过一系列的数学推导,即求得广义概率密度演化方程。
(24)

设初始条件为:
pZΨ(z,ψ,t0)=δ(z-z0)pΨ(ψ)
(25)
式中:pΨ(ψ)为Ψ的联合概率密度函数;δ(·)为Dirac函数;z0为确定性初始值。
进而,采用TVD格式的有限差分法可求得Z(t)的时变概率密度函数:
(26)
式中ΩΨ为Ψ的分布空间。
显然,所求的时变概率密度函数pZ(z,t)即反映了给定地震动强度与结构响应之间的概率分布关系。
3.3 概率密度演化方程求解的TVD格式
为方便讨论,取式(24)中的任一偏微分方程,记为:
(27)
针对形如式(27)的一维偏微分方程,采用有限差分法求解是行之有效的思路之一[19],且目前已发展了单边差分格式、Lax-Wendroff格式和TVD格式三种求解格式。其中,单边差分格式精度较低,耗散效应明显;Lax-Wendroff格式不能保证结果的非负性,色散效应突出;基于上述两种基本格式,并施加适当形式的通量限制器可求得具有总变差不增的TVD格式为:
(28)

(29)
式中:φ0(r)=max[0,min(2r,1),min(r,2)];

3.4 基本求解流程
目前,国内外已发展了多种结构易损性分析方法[20]。为了较为精细地考虑既有建筑结构的抗震性能,本文给出了采用贝叶斯方法进行材料参数更新,并基于概率密度演化理论研究信息更新结构的时变易损性分析方法,具体步骤包括如下。
(1)材料性能参数的贝叶斯更新:1)选取合理的材料物理性能经时变化模型作为先验预测信息;2)实测不同服役龄期建筑材料的实时物理性能;3)采用贝叶斯方法对先验模型进行信息更新,获得更符合实际情况的材料性能衰退模型。
(2)随机非线性力学模型的建立:1)建立不同服役龄期条件下结构的非线性力学模型;2)选取一系列满足场地条件的不同震级、不同断层距的地震动时程记录;3)分析结构参数、外部激励存在的随机性,确定随机变量的个数,进而采用数论选点法进行离散代表点的选取和赋得概率的计算。
(3)时变易损性分析:1)采用TVD格式的有限差分法求解广义概率密度演化方程,获得不同服役龄期、不同地震动强度作用下结构需求参数的概率密度分布函数;2)定义结构的破坏等级及相应的量化指标;3)计算不同服役龄期、不同强度地震作用下结构响应超过不同破坏等级限值的条件概率,进而绘制以地震动参数为变量的时变易损性曲线(面)。
4 算例分析
4.1 RC框架结构设计
本文以7层带内廊式对称三跨钢筋混凝土框架结构办公楼为例。结构设计使用年限为50年,建筑抗震设防类别为丙类;抗震设防烈度为8度(0.2g),Ⅱ类场地,设计地震分组第二组;地面粗糙度类别C类,基本风压0.3kN/m2。
框架结构平面布置如图2所示。结构底层层高3.9m,其余层层高3.3m。柱截面尺寸为0.55m×0.55m,梁截面尺寸为0.50m×0.20m,板厚为100mm。梁板柱混凝土强度等级均为C30。梁柱主筋采用HRB400级钢筋,梁柱箍筋、板采用HRB335级钢筋。梁柱混凝土保护层厚度20mm。填充墙为190mm厚的混凝土空心砌块,活荷载标准值按《建筑结构荷载规范》(GB 50009—2012)规定取值。

图2 框架结构平面布置图
采用YJK软件进行荷载组合、内力分析和截面配筋等初步设计工作。其中,结构的柱配筋见图3。

图3 结构的柱配筋示意图
4.2 混凝土经时强度更新的贝叶斯方法
文献[13]采用回弹法和钻芯法实测一般大气环境中不同服役年限民用建筑物的混凝土抗压强度。由于钻芯法更加准确,本文选取基于此检测得到的服役混凝土相对强度样本,如表2所示。当已知混凝土的立方体抗压强度标准值时,乘以相应的相对强度即得到混凝土时变强度标准值。

实测服役混凝土相对强度样本值 表2
将式(6),(7)视为先验预测模型,并通过式(8)建立混凝土经时抗压强度平均值和标准值的换算关系。图4为先验混凝土经时相对强度标准值的预测模型和实测样本值的对比。显然,采用牛荻涛模型[12]预测的混凝土经时强度标准值高于实测样本值,即该预测模型不能很好地预测混凝土经时强度的真实情况。若直接采用该模型进行结构非线性响应分析,预测结果将比真实情况更大,不利于对实际服役结构进行检修决策和优化加固设计等作业。

图4 先验混凝土经时强度预测值与试验值对比
根据贝叶斯方法,将表2中的实测数据样本值视为似然函数,并用其将先验预测模型进行多次修正,得到信息更新后混凝土经时强度的预测值,如图5所示。分析可知:贝叶斯方法可有效实现先验分布和实测数据的综合。一方面,更新后的模型曲线与先验预测曲线的发展趋势存在相似的变化规律,即贝叶斯方法继承了对先验分布理性规律的认识;另一方面,贝叶斯模型曲线与先验分布曲线存在一定的偏移,经过若干次贝叶斯更新即可使预测结果改善,使更新值更加接近实测样本值,即贝叶斯方法能充分考虑结构的实际服役情况。
将混凝土的经时抗压强度fcu(t)视为满足正态分布的随机变量,为了充分考虑材料的实际服役情况,采用贝叶斯方法对其均值进行参数更新(图5);而将钢筋的时变锈蚀深度视为确定性变量。故本文考察的7层RC框架结构中,将每一层混凝土的时变强度视为一个随机变量,共包含7个随机变量。表3列出了服役龄期条件下材料参数的基本时变信息。钢筋和混凝土采用第2节定义的经时材料本构关系模型。
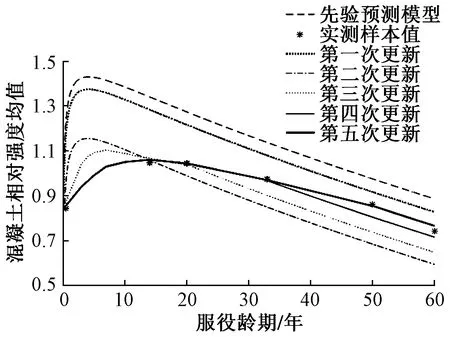
图5 混凝土经时相对强度均值的贝叶斯更新

不同服役龄期下的材料性能 表3
4.3 地震波的选取
地震波的合理选取直接影响结构易损性的分析效果。本文基于PEER地震动数据库,取场地剪切波速Vs,30为260~510m/s,对应中国的Ⅱ类场地[21]。选取的20条地震动记录均匀分布于以下5个地震动条带中[22]:1)SMSR(小震级、短距离):5.5≤M≤6.5,15km≤R≤30km;2)SMLR(小震级、长距离):5.5≤M≤6.5,30km≤R≤50km;3)LMSR(大震级、短距离):6.5≤M≤7.5,15km≤R≤30km;4)LMLR(大震级、长距离):6.5≤M≤7.5,30km≤R≤50km;5)NEAR(近场地震):6.5≤M≤7.5,0km≤R≤15km。其中M为震级,R为断层距,SA1为结构第一自振周期对应的加速度反应谱值。所选的地震波信息见表4。

地震动记录 表4
4.4 时变易损性分析

基于最大层间位移角的概率密度分布函数求得结构在不同服役年限、不同地震动水平、不同性能等级作用下的失效概率,采用分段三次Hermite函数拟合得到服役结构在不同服役龄期条件下地震易损性曲线如图6所示。为了更加直观地反映服役期对结构失效概率的影响,进而拟合得到三维时变易损性曲面如图7所示。

图7 时变易损性曲面
从图6可知,随着结构破坏程度的增加,结构易损性曲线在不同服役龄期之间的差异越大。如:当选用结构最大层间位移角为1/550时(完好),易损性曲线在不同服役龄期之间差异很小;而选用结构最大层间位移角为1/60时(不严重破坏),易损性曲线在不同服役龄期之间差异性较大。即当处于不同服役龄期的既有建筑结构遭遇“小震”作用时,其易损性曲线不会存在过大的偏差;而当其遭遇“大震”作用时,材料的实时力学性能很大程度上决定了结构的安全性。另一方面,结合表3可知,结构服役龄期分别为14年和20年时,钢筋均未发生锈蚀,而混凝土强度均值处于相当水平;而结构服役龄期分别为1年和50年时,50年混凝土的相对强度略大于1年时的相对强度,且1年时钢筋未发生锈蚀,而50年时钢筋则发生了程度不大的锈蚀。故而,在本文考察的6个服役龄期内,结构服役1年和50年、14年和20年生成的地震易损性曲线是大致一致的,即结构抗震性能相似。

图6 不同服役龄期条件的地震易损性曲线
综合分析图6和图7的结构时变易损性变化规律,可以发现:结构在服役初期,由于混凝土徐变、硬化等因素的影响,其强度处于增强的过程,在同一地面运动加速度作用下,其抗震性能随着服役龄期的增加而提高。结构服役龄期达10年左右,混凝土强度发展到较为稳定的阶段,并在今后10~20年之间处于平稳过程,该时期结构的抗震性能最好。结构服役龄期达25~30年时,混凝土强度开始降低,且钢筋开始锈蚀,其抗震性能开始呈现衰减的趋势。结构服役龄期为50~60年时(超过结构设计使用年限),混凝土强度呈现较为明显的降低趋势,且钢筋锈蚀仍持续发展,结构的抗震性能亦有一定程度的降低。
此外,可以注意到,传统的易损性分析方法通常假定结构地震需求参数服从对数正态分布,所得的分析结果只是经验近似值。而采用概率密度演化理论可直接分析求得地震需求参数的真实分布模式,其计算结果相较于传统方法应更加可靠。限于篇幅,图8仅给出了结构在服役龄期1年时分别采用本文选用方法与传统分析方法所得的地震易损性曲线。显然,当地震作用较小时,两种分析方法的计算结果差异不大;而当地震作用较大时,选用本文方法所得的失效概率略大于传统方法。即当地震作用较小时,可选用传统方法进行结构抗震性能分析,而当地震作用较大时,传统分析方法所求得的计算结果偏于不安全。

图8 服役龄期1年时地震易损性计算结果对比
5 结论
本文考虑材料性能的时变规律对结构抗震性能的影响,采用实测数据进行材料信息更新,对一考虑随机参数的7层RC框架结构进行时变易损性分析,结论如下:
(1)贝叶斯方法可有效实现先验分布和实测数据的综合,经过更新的贝叶斯数据既可保持已有理性认识的变化规律,又能更加接近实际服役情况。
(2)RC框架结构的抗震性能与材料的经时性能有关,前期抗震性能随着服役龄期的增加而提高,之后一段时期内保持在较为稳定的阶段,当服役龄期达到30年前后,由于材料性能的退化,结构的抗震性能随服役龄期的增加呈现降低的趋势。
(3)结构的时变易损性曲线在不同服役期是不一致的,且与划分的性能水平有关。随着结构破坏等级的增加,结构的易损性曲线在不同服役年限之间存在的差异越大。
(4)当地震作用较小时,采用本文方法与传统方法求得的结构失效概率差异不大;而当地震作用较大时,本文方法所得的结构失效概率略大于传统方法。
利用本文所提方法,可以求得满足实际概率分布的服役结构时变易损性,研究成果对既有建筑结构的检修决策和优化加固提供参考,具有良好的工程实用性。
