某锥形穹顶半刚接单层网壳分析与设计

何小辉，温四清，王 新，董卫国

(中信建筑设计研究总院有限公司， 武汉 430000)

0 引言

《空间网格结构技术规程》(JGJ 7—2010)[1]规定：单层网壳应采用刚接节点，以保证壳体几何不变，有效传递膜内力和弯曲内力。然而，实际节点是介于刚接和铰接之间的半刚接[2]。国内不少学者针对半刚接网壳开展了理论和试验研究[3-6]，但半刚接网壳在实际工程中应用较少。目前，半刚接网壳的设计尚缺乏规范依据，工程实施困难。以某图书馆的锥形穹顶单层网壳为研究对象，采用钢管相贯焊接节点。首先分析其受力变形性能和屈曲特性；接着对比研究不同截面方案和节点假定对构件承载力、屈曲特性和极限承载力的影响；最后采用多尺度有限元分析方法，真实反映节点性能对整体结构性能的影响，其分析结果可作为半刚接网壳的设计依据。

1 结构布置和有限元建模

穹顶结构由内环结构和外环结构构成，内外环跨径分别为26.4m和29.4m。内外环结构均为上下钢筋混凝土环梁与16根立柱形成的环形框架，内环结构通过单边悬挑梁支撑于外环结构上，外环结构则直接支撑于屋面大跨度预应力转换梁及悬挑梁上，外环结构的支撑刚度不均衡。锥形穹顶顶盖为16道径向主杆和环杆组成的肋环型单层网壳结构，穹顶矢高约3.7m，跨径为26.4m，矢跨比约1/7.1；环杆间距为1.1m，兼作为轻质陶瓦屋面系统的主檩。径向主杆与内环立柱间为铰接连接。16道径向主杆汇交中心采用截面为φ1 600×20的圆管相接，径向杆与环杆之间为直接相贯焊连接，均假定为刚接。图1为锥形穹顶结构剖面，图2为支撑穹顶的屋面层结构平面。表1给出了穹顶结构构件截面尺寸，钢构件材质均为Q345B；其中钢构件为矩形管，其余构件均为矩形混凝土截面。

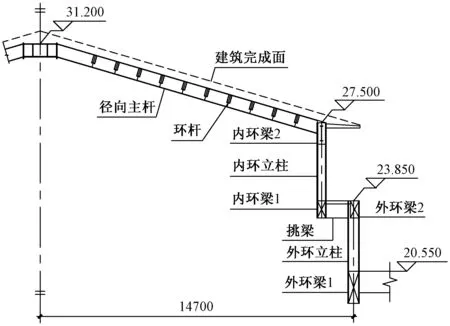
图1 锥形穹顶结构剖面

图2 支撑穹顶的屋面层结构平面

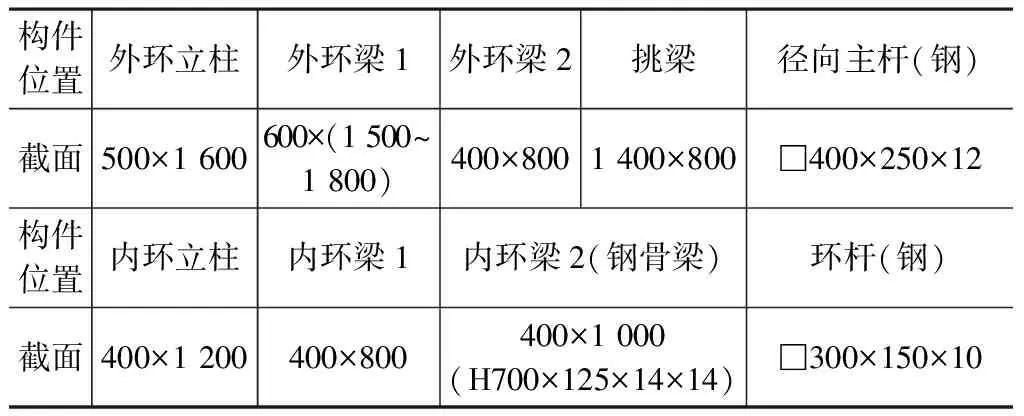
穹顶结构构件截面/mm表1

图3为结构整体计算模型，图4为穹顶结构独立计算模型，假定外环立柱下端固接，采用MIDAS进行计算分析。混凝土结构部分采用YJK进行计算和设计，本文从略。穹顶顶盖的钢构件按压弯或拉弯构件进行强度和稳定验算。径向主杆的计算长度系数μy=1.0，μz=0.1(构件几何长度L=13.75m，取径向主杆的斜长)，考虑了径向主杆汇交点的相互支撑作用和环杆的面外支撑作用。环杆的计算长度系数μy=1.6，μz=1.0(构件几何长度L=0.86～4.75m，取相邻主杆间的节间长度)。μy为绕与锥壳面法线垂直主轴的计算长度系数，μz为绕与锥壳面法线平行主轴的计算长度系数。

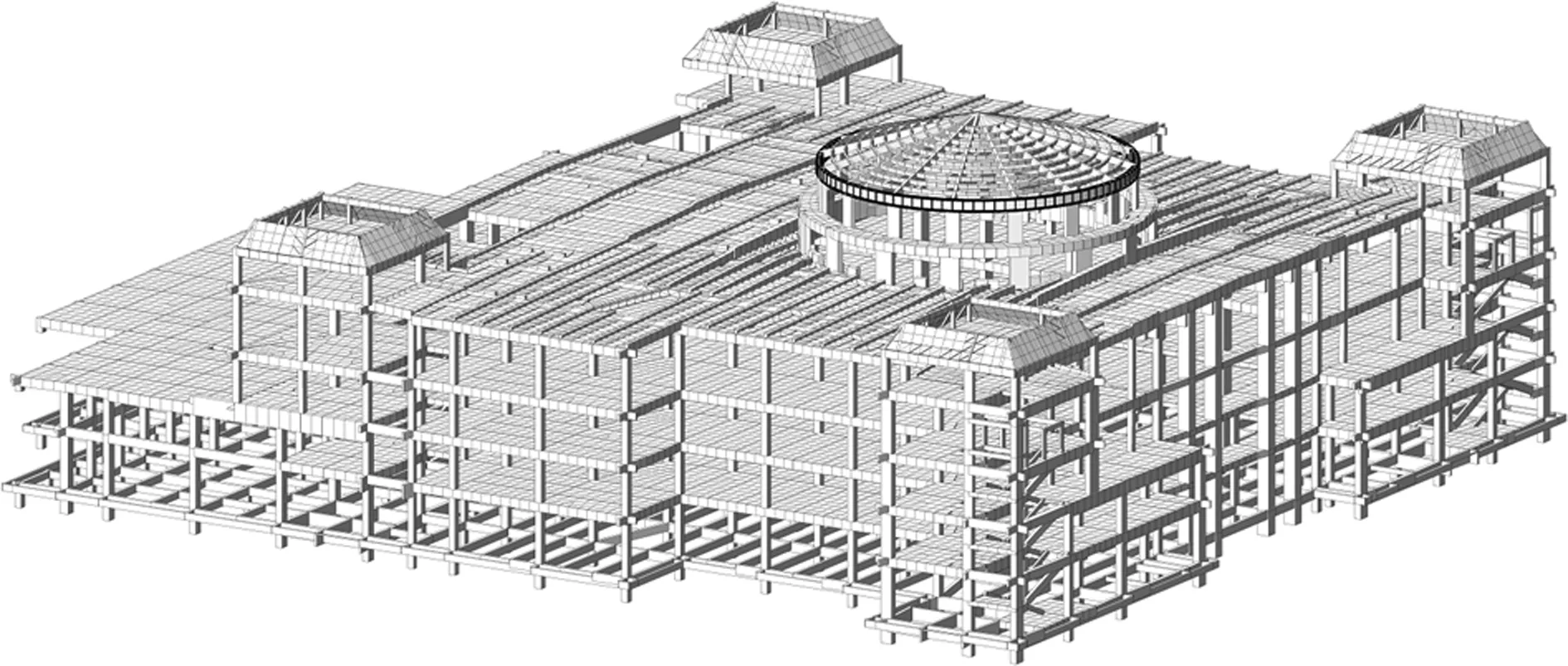
图3 结构整体计算模型(MIDAS)

图4 穹顶结构独立计算模型

2 穹顶结构的受力变形性能及屈曲特性

图5为标准荷载组合下穹顶的变形云图。从图中可以发现：1)整体模型的穹顶变形不均匀，南北两端的穹顶外缘变形较小，而东西两端的穹顶外缘变形较大，但最大变形出现在南侧1/4点处；2)穹顶结构独立计算模型的变形呈轴对称模式，最大变形位于锥面腰点处；3)穹顶的混凝土环梁的水平变形较小，环箍作用较强。

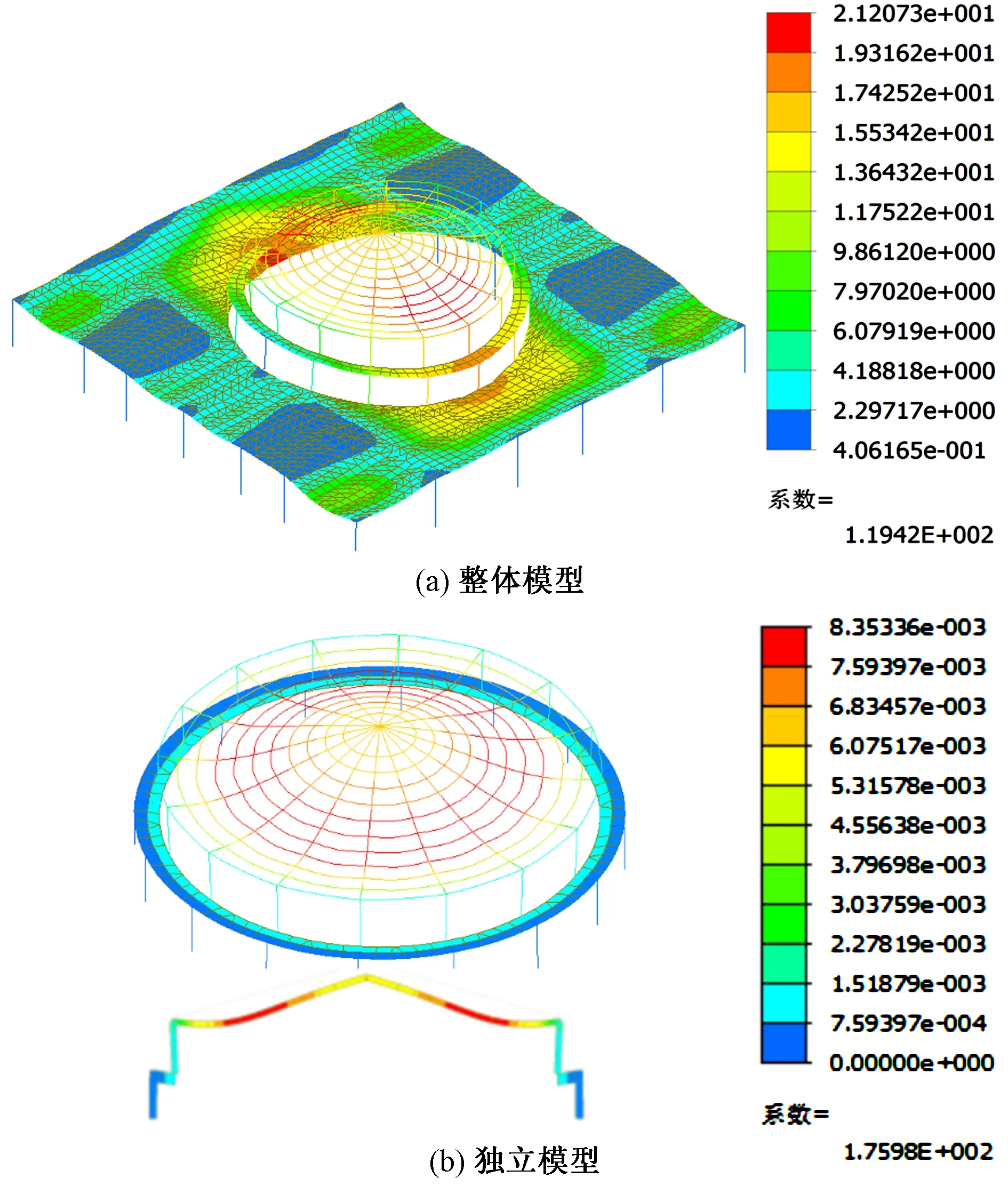
图5 穹顶变形云图/mm

图6为标准荷载组合下穹顶径向主杆的内力图。穹顶结构独立模型的16道径向主杆受力是完全相同的，而整体模型的下部支撑刚度不均衡，南北两端直接落在框架柱上，东西两端直接落在大跨度预应力梁上，支撑部位的竖向变形差将导致穹顶受力不均匀，且南北向的径向主杆与东西向的径向主杆具有不同的受力特点。穹顶结构的独立模型的径向主杆为压弯构件，轴力和弯矩均沿轴向变化，靠近两端支座的构件内力较大，而中心汇交点处的构件内力较小。整体模型的南北向径向主杆为压弯构件，靠近支座的轴力相当于穹顶结构独立模型的2倍，且中心汇交点处的构件轴力也大于穹顶结构独立模型的径向主杆。整体模型的东西向径向主杆则为拉弯构件，中心汇交点处的构件轴拉力最大，其弯矩分布与南北向主杆相似。另外，支座部位钢骨环梁为拉弯构件，整体模型中靠近南北端的构件轴拉力最大(约1 200kN)，相当于穹顶结构独立模型环梁的2倍。

图6 穹顶径向主杆内力图

对穹顶进行了特征值屈曲分析。作用荷载为：1.0恒载+1.0活载。图7为整体模型中穹顶结构的第1阶屈曲模态，屈曲系数λ=12.6，穹顶结构具有较好的整体稳定性能。从图7中可看出，钢穹顶发生整体反对称屈曲变形，南侧1/4穹顶下凹，北侧1/4穹顶上凸，中心汇交点为屈曲反弯点。对穹顶独立模型进行了特征值屈曲分析，前2阶屈曲模态与整体计算模型一致，表现为穹顶南北向凹凸或东西向凹凸，但屈曲系数λ=21.3，稳定性能明显提高。因此，穹顶下部支撑结构的刚度大小和分布均匀性将显著影响穹顶的整体稳定性能。

图7 穹顶第1阶屈曲模态(λ=12.6)

综合上述受力变形分析和屈曲模态分析，可将中心汇交点视作径向杆的支撑点，在未发生整体失稳前，径向主杆之间互为支撑。因此，径向主杆的计算长度可取为中心汇交点至外缘脚点间的距离。

3 杆件截面对穹顶性能的影响

结构构件截面直接影响结构刚度和承载力，也影响结构设计的经济合理性。为此从结构构件承载力、特征值屈曲性能、整体稳定极限承载力比和挠度等方面对比3种截面方案，具体截面方案见表2。由表2可知，方案A的用钢量相当于方案B的1.59倍，而方案C的用钢量相当于方案B的0.65倍。

构件截面方案 /mm 表2

表3为3种方案的分析结果。表中一阶挠度为一阶弹性分析结果，3个数据分别对应中心汇交点、腰部和脚点3个位置的竖向位移。屈曲系数λ均为特征值屈曲分析所得最低阶屈曲荷载与标准组合荷载的比值。一阶承载力比σ1为一阶弹性分析与设计所得径向主杆的最大验算承载力比。二阶承载力比σ2为二阶P-Δ弹性分析与设计[2]所得径向主杆的最大验算承载力比，计算长度系数同一阶弹性分析与设计方法。按第1阶屈曲模态考虑整体初始几何缺陷，缺陷最大值取为26 400/300≈88mm。采用弧长法进行考虑几何非线性的迭代计算。采用《空间网格结构技术规程》(JGJ 7—2010)[1]规定的考虑几何非线性的全过程分析，所得稳定极限承载力比ηu为极限承载力与标准组合荷载的比值。图8为部分关键节点(中点、南侧1/4点处、北侧1/4点处)的荷载-位移全过程曲线，其中图例后缀带“s”为独立模型。稳定极限承载力比ηu取北侧1/4点处曲线反向拐点对应的荷载系数η1和南侧1/4点处曲线按ECCS(欧洲钢结构协会)[7]取10%初始切线斜率确定的屈服荷载系数η2的较小值。

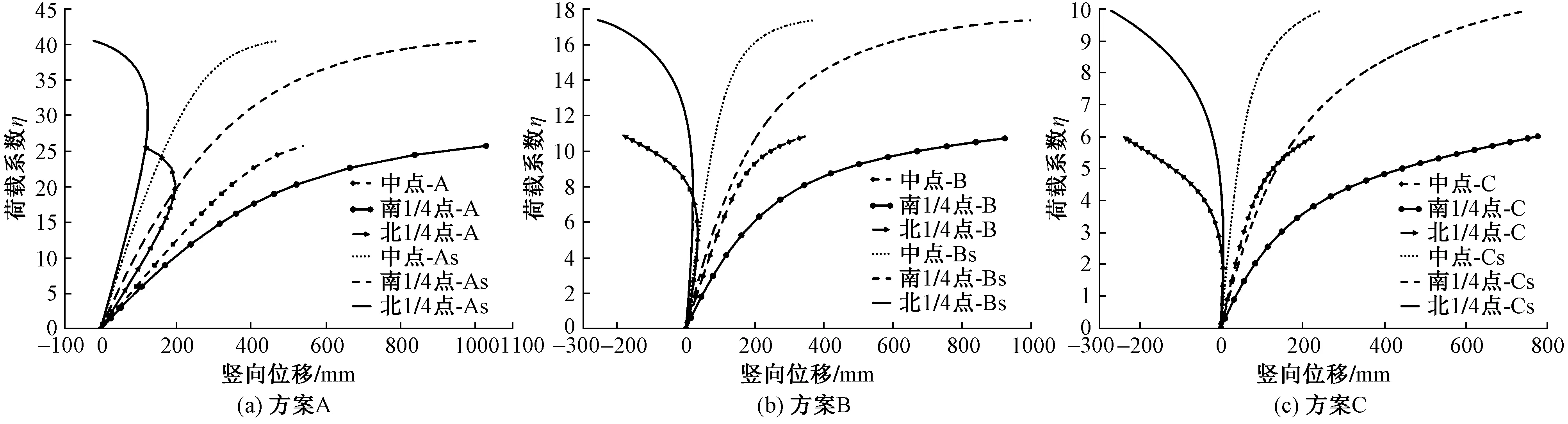
图8 穹顶关键节点的荷载-位移全过程曲线

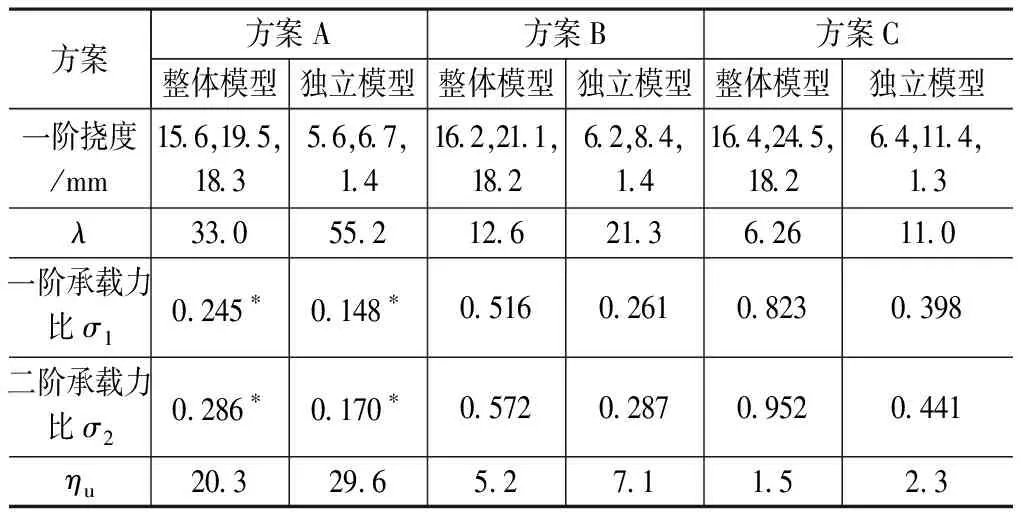
3种截面方案的计算结果对比表3

由表3的结果可知：1)穹顶的最大挠度均出现在腰点部位；2)独立模型的屈曲系数λ均远大于整体模型，不同方案之间的屈曲系数λ变化远大于挠度变化，结构整体稳定性能与构件截面刚度为非线性关系；3)独立模型的承载力比σ1，σ2均明显小于整体模型，比值σ2/σ1=1.1～1.17，即二阶P-Δ弹性分析结果较一阶弹性结果增大了10%～17%；4)不同方案之间的稳定极限承载力比ηu的变化幅度要大于一阶或二阶的承载力比和屈曲系数λ的变化；5)对于方案C，虽然承载力比σ1，σ2均小于1.0，但稳定极限承载力比ηu<4.2，不满足《空间网格结构技术规程》(JGJ 7—2010)[1]的要求。方案C的分析结果表明，空间结构的整体稳定性能仍需进行全过程分析复核，二阶P-Δ弹性分析所得承载力比小于1.0并不能确保结构的整体稳定性能。

从图8中可以发现，南侧1/4点处的变形大于中点，且增长较快；北侧1/4点处的变形则小于中点，且当荷载达到一定数值时出现位移反向，与第1阶屈曲模态的北侧上凸变形趋势一致。整体模型的刚度和承载力明显小于独立模型。方案C的北侧1/4点处的向下挠度很小，荷载作用下很快产生反向、上拱位移。基于结构刚度、承载力和整体稳定性分析结果，发现方案B具有可靠的安全性和较好的经济性。

4 节点假定对穹顶性能的影响

计算模型中的节点假定应与实际节点构造一致，构造复杂的重要节点应通过精细有限元分析确定其承载力[2]。本节考察了不同节点模拟假定对穹顶整体受力性能的影响。表4为模型编号及节点连接假定，表5为计算结果对比。图9为最低阶屈曲模态图，模型编号带“s”为独立模型。

从表4,5以及图9对比分析可以发现：1)中心汇交节点刚度对结构整体稳定性能和构件承载力比的影响较小，仅当环杆与径向主杆全部铰接时，中心汇交节点刚接会明显提高结构屈曲系数λ；2)环杆与径向主杆的节点刚度对结构整体稳定性能和构件承载力比的影响较大，节点铰接将明显降低结构整体性能；3)模型B2和B3的屈曲模态表现为相邻径向主杆交替凹凸起伏，且整体模型与独立模型的屈曲系数λ比较接近，比值σ2/σ1大幅增加，二阶效应增大，这明显不同于模型B和B1，表明环杆铰接导致穹顶结构的空间协同工作性能丧失或严重弱化；4)模型B4的分析结果表明，仅部分环杆与径向主杆刚接，结构便具有较好整体稳定性能，模型B4的屈曲模态与模型B和B1相似。

不同节点模拟假定模型 表4

图9 不同节点假定模型的最低阶屈曲模态

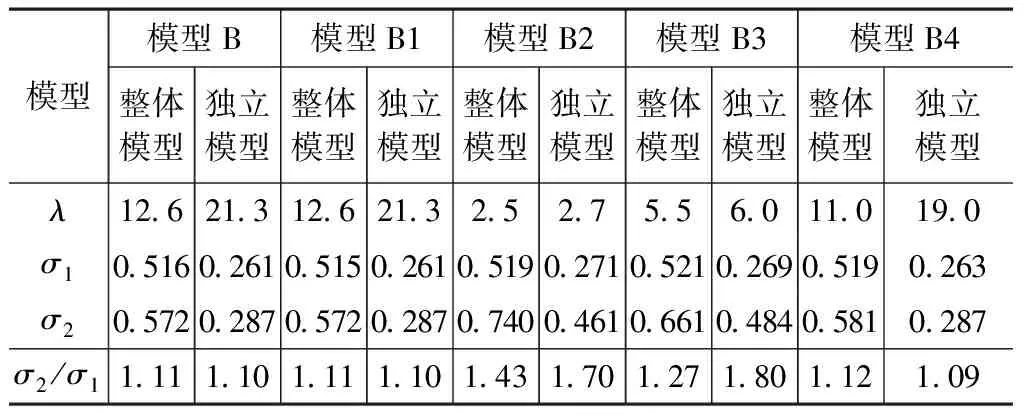
不同节点假定模型的计算结果对比 表5

5 多尺度模型真实模拟分析

钢管相贯焊接节点通常为半刚性节点，介于刚接和铰接之间。为了更加真实地模拟实际节点构造，本节开展了多尺度锥形穹顶有限元分析，可以反映实际节点刚度对结构整体性能的影响，可以考察节点细部的应力应变发展和评估节点承载能力。

采用MIDAS Gen的空间梁单元建立整体结构模型，采用MIDAS FEA有限元软件建立节点精细有限元模型，并导入MIDAS Gen整体计算模型。图10为中心汇交点和环杆与径向主杆的相贯节点，均采用板壳单元建模，单元尺度30mm。图11为多尺度结构有限元模型，在节点区以梁单元的端节点为主节点、以壳单元端截面的节点为从节点，建立6个自由度DOF全耦合约束关系的刚性面连接，实现梁单元与精细壳单元节点的变形协调和内力传递。本节分析模型编号为模型BF和BFs，分别为多尺度整体结构模型和独立模型。

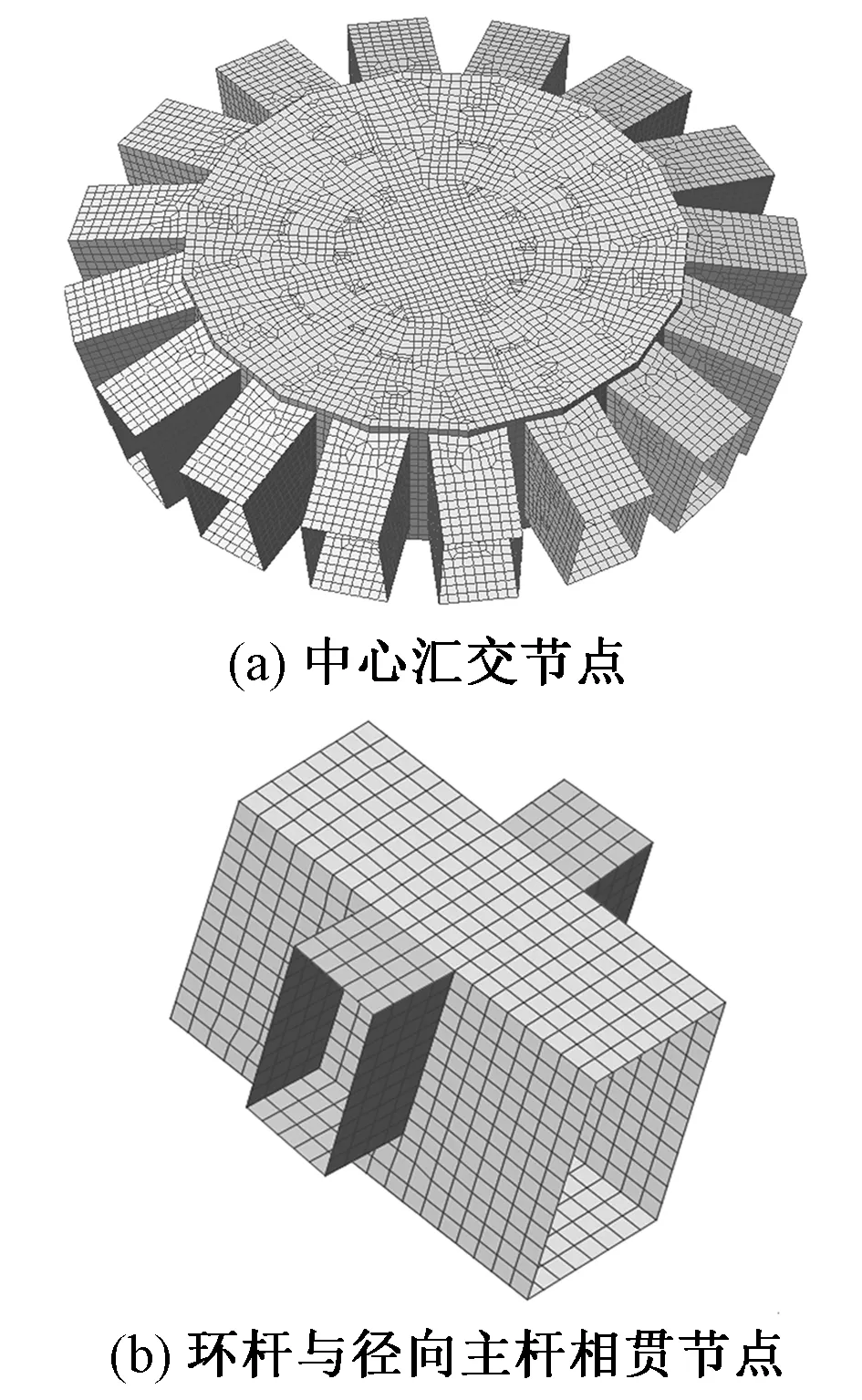
图10 节点精细有限元模型

图11 多尺度结构有限元模型

图12为模型BFs在荷载标准组合下的挠度云图，变形模式与模型Bs一致，梁单元与壳单元界面连接处不存在变形突变，整体结构变形协调。荷载标准组合下，模型BFs的穹顶最大竖向变形为10.7mm，大于模型Bs的8.4mm，小于模型B2s和B3s的11.0mm；模型BF的穹顶最大竖向变形为23.6mm，大于模型B的21.1mm，小于模型B2的25.0mm和模型B3的24.2mm。由此可见，真实模拟节点性能的多尺度模型的刚度介于节点刚接和铰接之间。经分析发现，相贯节点变形主要表现为弦杆壁板的凹凸变形，反映了节点轴向刚度和弯曲刚度的综合影响[8]。模型B2s和B3s的铰接低估了节点的抗弯刚度，且未能考虑节点的轴向刚度(或柔度)。

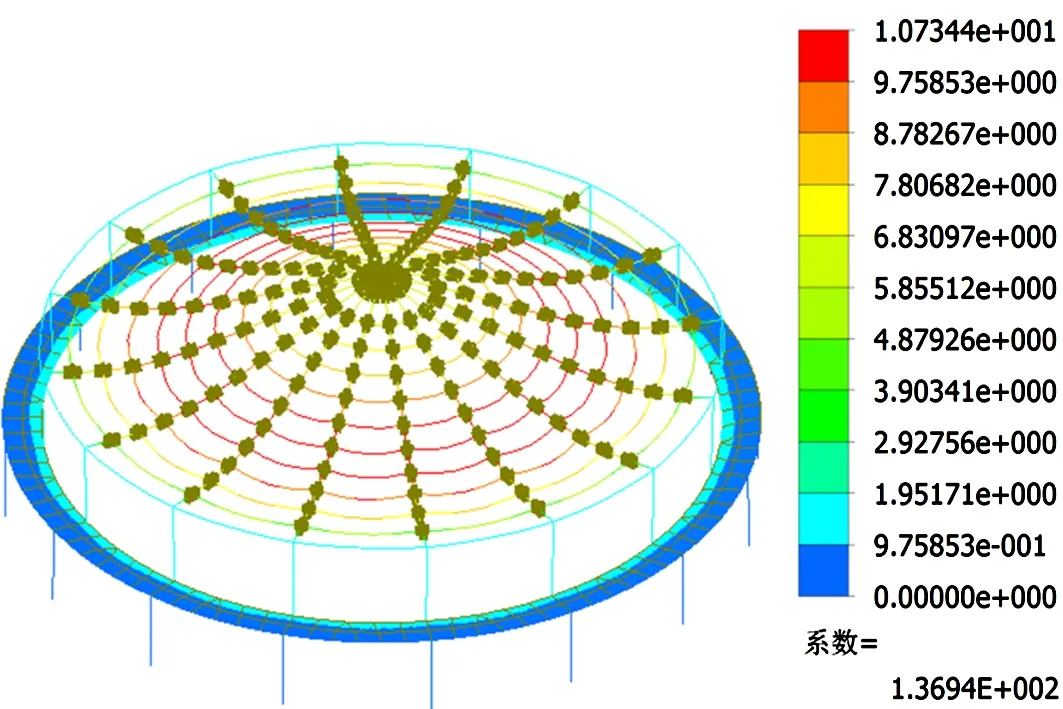
图12 模型BFs在荷载标准组合下挠度云图/mm

图13为多尺度模型的特征值屈曲分析结果。可以发现，多尺度模型BF(BFs)的最低阶屈曲模态与刚接模型B(Bs)的一致，均体现为穹顶的南北向凹凸变形，其屈曲系数λ比刚接模型稍有降低，但远大于铰接模型B2(B2s)和B3(B3s)。由此可见，该穹顶采用的相贯节点具有一定的抗弯刚度，能保证穹顶整体性和空间协同工作性能，不会出现铰接模型所表现的相邻径向主杆交替凹凸起伏的屈曲形式，具有较好的整体稳定性能。

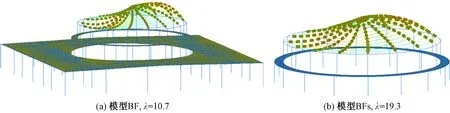
图13 多尺度模型最低阶屈曲模态

图14为多尺度模型考虑几何非线性的穹顶关键节点的荷载-位移全过程曲线及与刚接模型的对比。经对比可以发现，多尺度模型的结果曲线与刚接模型相似，但刚度和极限承载力均有所降低。分析可得多尺度模型BF的稳定极限承载力比ηu=4.38>4.2，可满足规范要求。图15给出了荷载系数2.0时模型BF的节点von Mises应力云图。可以发现，相贯节点的壁板发生局部凹凸变形，中心汇交点和环杆与径向主杆相贯节点均处于弹性受力状态，最大应力分别为229MPa和297MPa，小于Q345钢的屈服强度。因此，该穹顶的相贯焊接节点可以满足承载极限状态下的承载力要求。

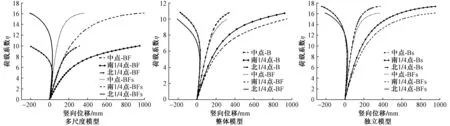
图14 多尺度模型中穹顶关键节点的荷载-位移全过程曲线

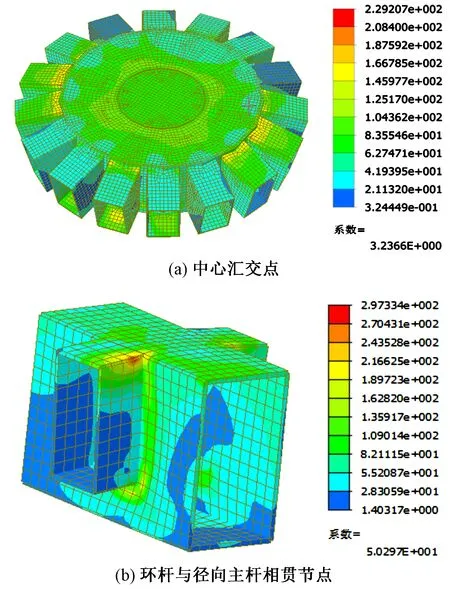
图15 节点von Mises应力/MPa(η=2.0)

6 结论与展望

(1)采用肋环型网格的锥形穹顶单层网壳具有较好的空间协同变形性能，整体失稳模态呈“S”凹凸双波屈曲模式，中心汇交点为屈曲反弯点。

(2)采用钢管非加劲相贯焊连接的单层网壳为典型的半刚接网壳，合理的杆件截面设计可使其整体稳定性能接近于节点刚接模型。

(3)节点铰接会改变单层网壳的屈曲形态，使结构整体协同性能严重弱化或丧失。

(4)多尺度有限元分析是判别节点刚度和承载力的有效分析方法，可真实反映节点性能对整体结构性能的影响。

(5)采用二阶P-Δ弹性分析所得承载力比小于1.0并不能确保结构的整体稳定性能。空间网格结构的整体稳定性能仍需进行全过程分析复核。

钢管非加劲相贯焊连接构造简单，施工方便，外观美观。若在主管内设置内隔板或壁板贴焊补强板以使节点满足刚接要求，则会极大地增加加工制作和焊接工作量。本工程采用的钢管非加劲半刚接单层网壳，既能满足承载力和稳定性要求，又能简化施工、降低造价，其研究成果可为相关工程设计和科研人员提供参考。