预应力方桩水上沉桩定位控制及计算解析

石正伟，蒋永辉

（中交上航（福建）交通建设工程有限公司，福建厦门 361000）

1 工程概况

1.1 概述

工程所在地霞浦县海岛乡西洋岛，地处霞浦县东南海域，距霞浦县城约20 nm，面积约7.9 km2。本项目码头位于北澳港区东防波堤内侧，与护岸通过栈桥连接。

1.2 布置形式

码头总长度142.49 m，分4 个结构段，单个结构段长35.6 m，宽18 m，每个结构段均为4 跨，设5 榀排架，排架间距7.7 m，两端悬臂长均为2.40 m，共计20 个排架。码头共有600 mm×600 mm 预应力方桩117 根（含备桩2 根），桩长为20～60 m；其中直桩47 根，斜桩68 根，斜桩包括1:4 及1:5 两种比例，相对码头平面横纵轴线的扭角包括15°、17°及20°三种。

图1 码头平面布置示意图

1.3 施工条件

1）潮位

港池内泥面平均标高-0.5 m，设计最高潮位6.66 m，设计最低潮位0.66 m，水深在1.16～7.16 m；打桩船吃水深度为2.5 m，运桩船吃水深度为4 m，潮位2.0 m 以上时方可满足打桩船作业要求。

2）地质条件

根据勘察孔揭露的地质资料，地基土主要可分为5 个岩土层，分别为淤泥、粉质粘土、全风化花岗岩、强风化花岗岩以及中风化花岗岩。每层岩土层呈较大坡度向下延伸，且施工过程中伴随着夹层，地质情况较复杂。

2 主要施工方法与难点

2.1 施工方法

本工程预应力方桩采用“合力桩3”船进行施打，由20 排架至1 排架呈梯形由F 轴至A 轴进行施工。在有效的作业时间内，为保障施工质量，加快施工进度，根据设计图纸每根桩的参数，立桩入龙口前应提前架设调整好陆上测量仪器，减少校核时间，提高每日施打方桩数量，以尽快形成排架进行上部横梁混凝土浇筑。

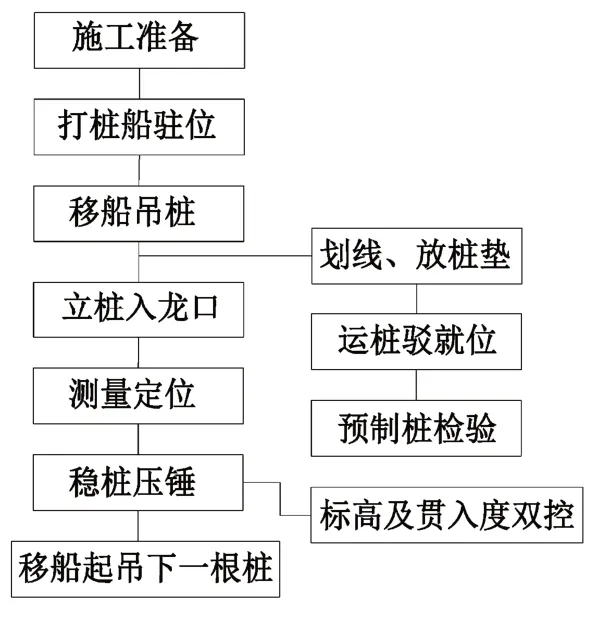
图2 沉桩施工工艺流程

2.2 施工难点

本工程预应力方桩水上沉桩施工位于北澳80 HP 码头，施工中伴随着赶潮水作业、地质条件复杂两大施工难点，每日有效作业时间短、插桩后定位精度偏差大，为保障施工质量，加快施工进度，一方面要提前布设测量仪器并保证零失误，另一方面根据陆上测量校核结果加强与船上人员沟通交流，不断调整方桩的位置方向，在保证沉桩精度符合设计要求的前提下，提高每日施打方桩数量，为后续上部横梁施工打下基础。

为提高方桩沉桩精度，减少因偏位过大而影响后续施工进度，方桩沉桩控制采用船载GPS 定位及陆上测量校核的双控保障机制。陆上测量采用一台经纬仪加一台全站仪，由于每根方桩的施打位置不一样，每次均需调整测量仪器至合适位置。综合现场实际情况，抛开测量仪器的架设时间，对于斜桩来讲，在全站仪后方交会完成后，需要根据交会形成的坐标高程推算斜桩该高程的平面坐标。为减少测量人员现场工作计算时间，降低计算出错率，有效提高现场沉桩的精准定位及施工速度，通过了解沉桩定位控制方法及解析计算过程，并最终形成一套简易快速的条件判定公式变得尤为重要。

3 定位控制方法

在确保平面扭角正确的前提下，任意两条相交线可确定该桩的平面位置，即通过架设两台仪器观看桩身任意一已知点A（Xa，Ya，Za）便可估算出桩的偏移方向及偏移量。

通过设计图可知该桩设计标高处的平面坐标。将直桩沿垂直方向投影，该面不受高程影响，即可直接得出桩身任意高程处平面坐标；反之，斜桩随着高程不断变化，投影面也在随着变化，需通过系列计算方可得出桩身任意高程处平面坐标。

3.1 直桩定位控制

已知该桩设计标高，选择该面上已知点A（Xa，Ya，Za），沿桩身做两条延长线，不难发现，此延长线上的点均为已知点。

选择该延长线上2个已知点输入RTK进行直线放样，在陆上合适位置处架设仪器并通过观测已知点位置调整观测方向，保持仪器及观测方向在放样直线上，此时观测不受高程影响，任意上下旋转目镜均可作为桩身的偏位校核。

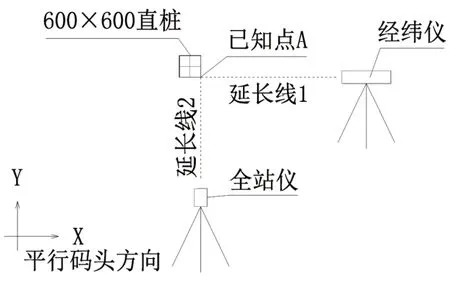
图3 直桩定位控制

3.2 斜桩定位控制

已知该桩设计标高，取桩身已知点A（Xa，Ya，Za），沿桩斜度方向做A 点延长线1，不难发现，延长线1上任意两点作为已知点输入RTK进行直线放样时，在陆上合适位置处架设仪器并通过观测已知点位置调整观测方向，保持仪器及观测方向在放样直线上，此时观测不受高程影响，任意上下旋转目镜均可作为桩身的偏位校核。

在观测另一个方向即延长线2（非斜度方向），该观测点受高程影响。此时选择合适位置处架设好全站仪，通过后方交会形成一个已知点坐标C（Xc，Yc，Zc），调整保持全站仪目镜水平（即垂直角为0°）。此时C 点与B 点高程相等，即可通过该高程推算桩身任意一点B（Xb，Yb，Zb），为易于观测偏移情况，可选择角点进行观测。将B 点坐标输入已架设调整完毕的全站仪中进行放样测量，此时只需水平转动全站仪，待仪表盘dHA 即目标与待放样点的水平角差值为0 时，全站仪十字丝中心对准点即为B 点。

图4 斜桩定位控制

3.3 计算方法

直桩2 个方向观测均不受高程影响，斜桩只沿斜度方向观测不受高程影响，另一个方向需通过计算得出未知点B 坐标后方可进行观测，以本工程为例，相关计算过程为：由设计图纸可知，该桩设计标高任一点A（Xa，Ya，Za)，随着高度变化，求桩身任意高程一点B（Xb，Yb，Zb）。

由于本工程拟建高桩码头平行和垂直码头方向（即XY 坐标系）与设计测量控制网（即NE 坐标系）并非完全重合，存在一定夹角，由于斜桩有相对于码头的平面扭角，为确保计算精准，先将其转换于设计测量控制网中，相关参数为：β=2°3′32″=2.059°，γ=α-Z·90°，δ=γ-β。α 为以码头X轴为起点逆时针旋转的平面扭角；β 为码头XY 坐标系与NE 坐标系的夹角；γ 为不影响后续计算而设定的一个角度，大于0°且小于90°；Z 为整数，-1,0,1,2,....；δ 为以E 轴为起点逆时针旋转的平面扭角。

图5 平面扭角转换

1）以桩中心点为0 点，当α 位于第一、三象限时，对应于图 6 中编号③，|△X|=S·cosδ，|△Y|=S·sinδ，即|△X|=|Zb－Za|/i·cos（α－β－Z·90°），|△Y|=|Zb－Za|/i·sin（α－β－Z·90°）。

图6 计算方法

2）以桩中心点为0 点，当α 位于第二、四象限时，对应于图 6 中编号④，|△X|=S·sinδ，|△Y|=S·cosδ，即|△X|=|Zb－Za|/i·sin（α－β－Z·90°），|△Y|=|Zb－Za|/i·cos（α－β－Z·90°）。

其中：S=|Zb－Za|/i；Za 为已知点A 点高程；Zb 为通过全站仪后方交会形成的未知点B 点高程；S 为投影长度；i 为桩身斜度；可得Xb=Xa+△X，Yb=Ya+△Y，即可求出未知点B（Xb，Yb，Zb）。

3.4 正负条件判定

通过上述计算公式，可知△X 与△Y 可正可负，为提高测量控制进展效率，在计算完成△X 与△Y的绝对值后，根据平面扭角，可确定该扭角位于第几象限，比较设计已知点A 高程Za 与全站仪交会形成的已知点C 高程Zc 的差值，即可快速得到△X与△Y 的正负情况，代入推导公式可得到未知点B点的坐标，将该点输入全站仪，旋转到位后观测该方向的偏移情况。

表1 正负判定表

为方便记忆正负情况，设定设计标高中心处0点至桩尖方向为正方向，至桩顶方向为负方向，如图7，不难发现，当未知点高程大于已知点高程时，未知点位于负方向上，以α 位于第1 象限为例，此时未知点位于第3 象限内，即△X 为负、△Y 为负；当未知点高程小于已知点高程时，此时未知点位于第1 象限内，即△X 为正、△Y 为正。

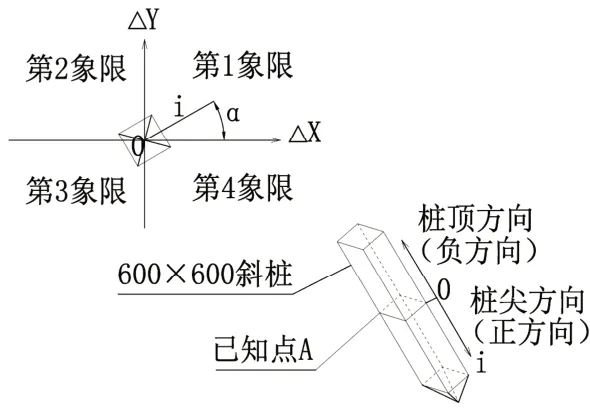
图7 正负判定

3.5 成果总结与现场运用

1）成果总结

综上所述，通过对直桩、斜桩定位控制方法的了解并解析计算过程，最终形成一套简易快速的条件判定公式（见表2），将成果表运用于现场实际沉桩定位控制，减少测量人员现场工作及计算时间，降低计算出错率，并有效提高现场沉桩精准定位及施工速度。

表2 成果表

2）现场实例计算

取斜桩7-C 为计算实例，已知相对于码头的平面扭角α=253°，

桩身斜度i=4:1，桩设计标高1.5 m，取桩身一已知点A（505357.3137，2934711.2688，1.5），假设全站仪后方交会后形成的坐标C 的高程Zc=7.5 m，即待求点B 点高程Zb=7.5 m。已知以上参数，求桩身B 点坐标（Xb，Yb，Zb）。

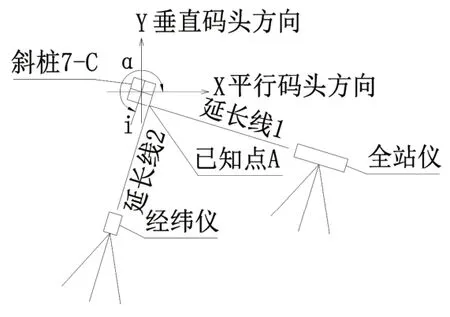
图8 斜桩7-C 计算

以桩中心点为0 点，此时α 位于三象限，又Zc＞Za，根据表2，可得△X＞0，△Y＞0；此时

即求得桩身待观测点 B（505357.8035，2934712.6866，7.5）。

4 结语

在受潮水、地质等因素影响下，每日有效作业时间短、插桩后定位精度偏差大，为保证沉桩施工质量进度，提高每日施打方桩数量，在对每根桩的陆上测量校核时，我们需要做到快速准确无失误，由于设计提供的坐标是在设计标高条件下的桩中心点坐标，而中心点仪器无法观测到，由此需将设计坐标转换为角点坐标方便观测，因此需要使用文中提出的方法来实现。

在后方交会完成后可通过调整仪高拟定统一的2～3 个观测标高，将本文成果表运用于现场实际，提前计算每根斜桩的角点坐标，并形成坐标一览表，方便放样时随时调出使用。通过运用本文提出的方法及成果，有效降低无规律计算导致的出错率和对沉桩施工质量进度的影响，极大地保障施工的流畅性，提高测量控制工作及现场沉桩施工质量及效率。