水平地震作用下全直桩码头底梁作用影响分析

汪 雨，孙克俐

（天津大学港口海岸及近海工程系，天津 300350）

引言

全直桩梁板式码头具有透空性好、对河流泄洪影响较小、施工速度较快、工程造价较低等优点，在内河码头建设中得到广泛的应用。然而，该结构上的水平力全部由直桩承担，而直桩抵抗水平力的能力相对较弱；在较大水平力的作用下，结构侧向位移可能超过容许值。因此，针对这一系列特点，在该结构基础上增设底梁形成一种新型结构，可有效提高码头结构的整体性及水平承载能力。

近年来，就该结构的静动力性能已开展了相关研究。在静力性能方面，任启江[1]等对比分析了水平撞击力作用下有无底梁及有无靠船梁全直桩码头单横向排架的受力变形特性；卢陈[2]针对某有底梁全直桩码头进行了物理模型试验，通过相似理论推导和配比试验确定合适的模型材料，通过分级加载的方式，研究不同大小水平力作用下结构侧移和桩身弯矩的变化规律。在动力性能方面，刘晓平[3]等对比分析了有无底梁全直桩结构前三阶的振型特点，发现有底梁结构的自振振幅更小、固有频率更大，结构的整体刚度有所提升，但未对结构的动力性能进行深入探讨。

底梁式全直桩码头结构在我国主要应用于长江中上游水位差较大的地区，而这些地区也是地震频发区，但目前关于该种结构抗震性能及其中底梁作用影响的研究相对较少。本文在保持码头材料体积基本相同的情况下，分别对全直桩单层梁结构和双层梁结构进行地震反应谱分析，研究底梁对全直桩码头地震响应特性的影响，为工程实践中该结构的抗震设计提供参考。

1 模型建立

1.1 模型尺寸

本文选取某全直桩码头的一个结构段（3 跨4榀排架）作为研究对象，分别建立单层梁和双层梁全直桩码头结构模型，如图1 和图2 所示。模型整体坐标为笛卡尔坐标系，x 轴平行于码头前沿线，y轴垂直于码头面向上为正，z 轴垂直于码头前沿线由陆侧指向水侧。码头面顶高程5.0 m，前沿设计底高程-10.0 m，桩底标高为-31.0 m。码头结构段长度为26.6 m，横向排架间距8.2 m，各横向排架中直桩间距6.6 m；桩基为直径1.2 m、厚度17 mm 的钢管桩；面板厚度0.3 m。单层梁结构模型中，横梁截面尺寸为1.0 m×1.5 m，纵梁截面尺寸为0.8 m×1.4 m。双层梁结构模型中，底梁位于顶梁下方9 m 处；为保持材料用量与单层梁结构基本相同，顶横梁截面尺寸缩减为0.8 m×1.2 m，顶纵梁截面尺寸缩减为0.6 m×1.1 m；底横梁截面尺寸为0.5 m×1.0 m，底纵梁截面尺寸为0.5 m×0.9 m。

图1 单层梁全直桩码头有限元模型

图2 双层梁全直桩码头有限元模型

1.2 材料参数

本文采用振型分解反应谱法计算两种结构在水平地震作用下的动力响应。考虑到反应谱法中只有线性行为是有效的，码头中钢筋混凝土结构和钢管桩均采用线弹性本构模型，构件材料属性见表1。

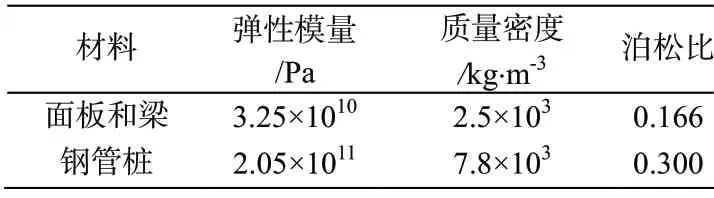
表1 结构材料参数

1.3 计算单元及边界条件

采用壳单元SHELL43 模拟面板，采用梁单元BEAM188 单元模拟纵横梁和桩基，通过定义截面偏移模拟梁板间的实际相对位置。采用质量单元MASS21 模拟码头面上的堆载附加质量（30 kN/m2）。采用垂直于桩轴向的弹簧单元COMBIN14 模拟桩侧土对桩的约束作用，根据《港口工程桩基规范》[4]，按地基抗力系数随深度增长的线弹性地基法—m 法进行模拟。

码头结构各构件之间通过共节点实现整体的刚性连接；考虑到桩基为嵌岩桩，故将桩底部设置为固结。

1.4 地震反应谱的选取

本码头所在区域地震设防烈度为7 度，场地复杂程度等级为Ⅱ级。结构阻尼比为0.05，水平向地震系数0.1，采用《水运工程抗震设计规范》[5]中的β谱曲线进行水平地震响应分析，反应谱特征周期为0.35 s。

2 底梁作用影响分析

2.1 底梁对结构自振特性的影响

单层梁和双层梁全直桩码头结构前10 阶固有频率随模态阶数的变化曲线如图3 所示。

图3 两种结构固有频率变化曲线

由图3 可知，单层梁和双层梁全直桩码头结构的固有频率变化趋势基本相似，随阶数递增均呈分段集中分布。两种结构的固有频率在前三阶模态的变化幅度均较小，在第三阶与第四阶模态间均发生明显跃升，而后随着模态阶数的增加逐步增大。但双层梁结构的固有频率明显大于单层梁结构，随着阶数的递增，两种结构固有频率的差值越来越大。而结构的固有频率一般与其刚度成正比，可见布设底梁可以显著提高全直桩码头结构的整体刚度。

2.2 底梁对结构位移响应的影响

沿码头横向分别对单层梁和双层梁全直桩码头结构进行水平地震动激励，并按SRSS 法进行效应组合，得到两种结构位移响应如图4 所示。

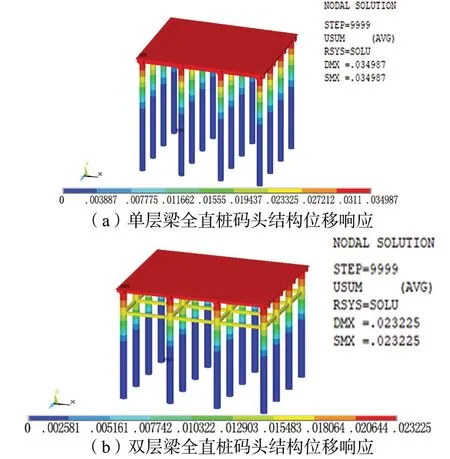
图4 水平地震作用下两种结构的位移响应

由图4 可知，在相同烈度的水平地震作用下，双层梁结构最大位移为23.2 mm，相比于单层梁结构的最大位移（35.0 mm）减小了约33 %。两种结构的最大位移均发生在最左侧排架近海侧桩基顶部，将该桩命名为1 号桩。两种结构中1 号桩侧向位移沿桩身变化规律如图5 所示。

图5 两种结构桩基位移对比

由图5 可知，相同地震荷载作用下，单层梁和双层梁全直桩码头结构桩侧向位移沿桩深的变化规律基本相似，从桩底到桩顶位移均呈逐渐增大的趋势，并在桩顶处达到最大值。但相比于单层梁结构，双层梁结构桩位移的增大趋势在底梁以上部分明显减缓；而桩基的侧向位移一般与其刚性系数有关：刚性系数越大，侧向位移越小[6]。因此，布设底梁可以增大全直桩码头桩基顶部的法向位移和转角位移刚性系数，进而提高上部结构的抗侧刚度，有效减小结构的侧向位移。

2.3 底梁对桩基内力的影响

在相同烈度的水平地震作用下，单层梁和双层梁全直桩码头结构1 号桩剪力对比见图6。

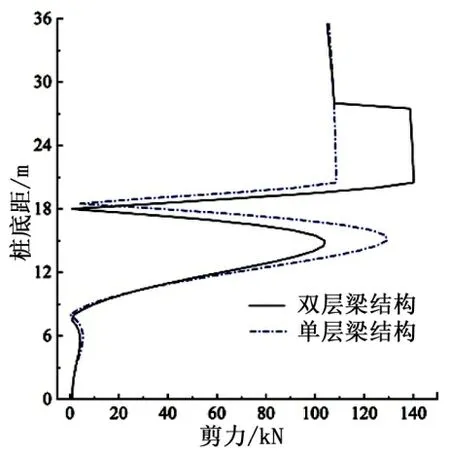
图6 两种结构桩基剪力对比

由图6 可知，两种结构的桩身剪力值在桩顶至底梁上方这一段基本相近；但在底梁下方到泥面这一段，双层梁结构的桩身剪力值由于在底梁连接处发生突变而大于单层梁结构；在泥面下方，双层梁结构的的桩身剪力值则明显小于单层梁结构。

在相同烈度的水平地震作用下，单层梁和双层梁全直桩码头结构中1 号桩弯矩对比见图7。

图7 两种结构桩基弯矩对比

由图7 可知，两种结构桩身弯矩均在桩基顶部与泥面附近出现峰值点，其中，双层梁结构的桩顶弯矩值相比于单层梁结构减小了约40 %，泥面下弯矩峰值减小了约20 %。与单层梁结构不同的是，双层梁结构桩身弯矩在底梁与桩基连接处附近发生局部突变，出现了一个与桩顶弯矩值大小相近的峰值点。

分析表明：双层梁全直桩码头结构中，底梁与顶梁共同传递水平地震力，一方面使得较大的地震力转变成了较小的分散力作用在桩基上，限制了桩端的剪切变形，使得桩基受力更为均匀，泥面下桩弯矩和剪力均减小；另一方面水平力分散到更低的位置进行传递，减小了结构柔度，提高了结构刚度，桩顶弯矩减小。另外，布设底梁会导致桩基与底梁连接处出现剪力突变及弯矩峰值，在结构设计中需要重点关注，保证该处具有足够的承载能力。

2.4 底梁对横梁轴力的影响

由分析可知，双层梁结构中，底横梁主要起到和顶横梁共同传递水平力的作用。因此，下面取1号桩上部横梁为研究对象，就增设底梁对于顶横梁轴力的具体影响进行分析。单层梁和双层梁全直桩码头结构顶横梁轴力分布如图8 所示。

图8 两种结构顶横梁轴力对比

由图8 可知，在相同烈度的水平地震作用下，单层梁和双层梁结构顶横梁轴力的变化规律基本相似，由于桩的抗弯作用，两者的轴力值在桩后均呈急剧减少的趋势。相比于单层梁结构，双层梁结构顶横梁两端的轴力值明显减小，而中部的轴力值则有所增大，总体轴力峰值减小了约20.8 %，改善了单层梁结构横梁两端轴力明显大于中间的问题。可见增设底梁后，可以有效减小顶横梁轴力，使其分布更加均匀，进而对码头上部结构受力有利。

3 结语

本文从结构位移、桩基内力、横梁内力三个方面，对单层梁和双层梁全直桩码头结构进行水平地震作用下的对比分析，得出以下结论：

1）在码头材料用量基本相同的情况下，选择增设底梁的双层梁结构，可以提高结构的整体刚度，增大结构的自振频率，有效减小结构侧向位移，有利于码头的安全使用。

2）增设底梁后，桩顶弯矩值明显减小，有利于桩顶与横梁连接接头处理；但桩基与底梁连接处会出现弯矩峰值及剪力突变，在设计中需重点关注该处桩的承载情况。

3）相比于单层梁结构，双层梁全直桩码头结构的桩基及顶横梁内力分布更为均匀，有利于充分发挥构件强度，进而提高结构的抗震能力。