一类时滞SIR和SIS传染病组合模型行波解存在性分析
2021-08-25付其飞李庶民
付其飞, 李庶民
(昆明理工大学 理学院, 云南 昆明 650500)
传染病一直是危害人类健康的重要因素之一,随着现代科学技术的进步,许多流行病都得到了控制,但还有一些流行病没有得到有效控制,依旧影响着人们的生活。有些流行病具有一定的潜伏期,例如新冠病毒肺炎,因此,对于具有潜伏期流行病的研究具有重要的意义[1-2]。为了更好地了解各种疾病的传播速度和方式,对传染病的行波解存在性和动力行为的讨论成了一个热门的研究方向。例如,Wang等[3]考虑了Kermack-McKendrick扩散模型的行波解存在性问题,Li等[4]研究了非局部扩散的传染病模型。文献[5]研究了一类复杂金融网络风险传染模型,本文将其引入到传染病模型中,研究传染病模型行波解的存在性,并考虑了因病死亡率、疾病潜伏期和空间的扩散[6-9]。
1 模型与假设
本文在文献[5]的基础上考虑如下的一类具有时滞的非局部扩散传染病系统:
(1)


系统(1)的初始条件为S(x,t)=ρ1(x,t),I(x,t)=ρ2(x,t),R(x,t)=ρ3(x,t),t∈[-τ,0]。
2 行波解的存在性
(2)
令N=S+I+R,则系统(1)变为:
(3)
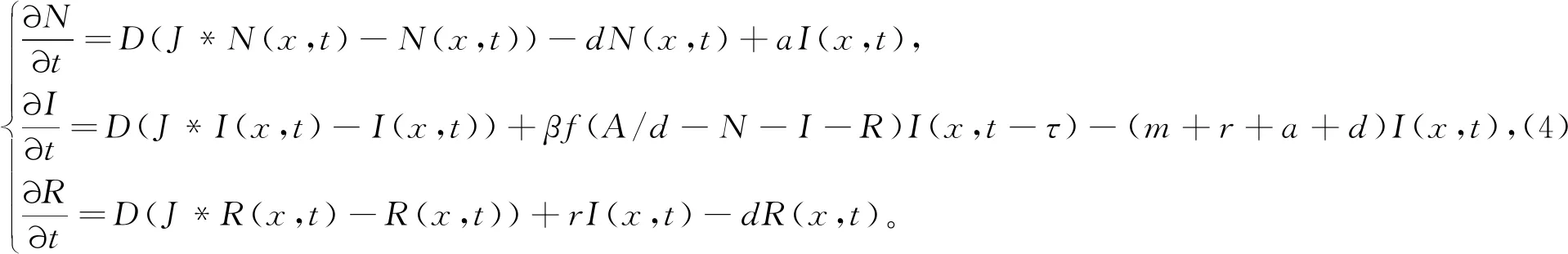
如果R0>1,系统(4)有两个稳定点(0,0,0)和(k1,k2,k3),其中k1=A/d-S*-I*-R*,k2=I*,k3=R*。系统(4)的行波解形式为(N(x,t),I(x,t),R(x,t))=(φ(t),φ(t),ψ(t)),其中t=x+ct。
令fc1=aφ(t)-dφ(t),fc2=βf(A/d-φ(t)-φ(t)-ψ(t))φ(t-cτ)-(r+m+d+a)φ(t),fc3=rφ(t)-dψ(t)。则系统(4)为
(5)
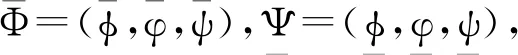
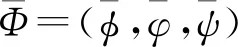
令C[0,M](R,R3)={Φ(t)=(φ,φ,ψ),t∈C(R,R3),0≤Φ(t)≤M,t∈R},当Mi≥ki(i=1,2,3)时,满足
下面寻找系统(5)的行波解。

(A2)存在3个连续的正数Li(i=1,2,3),有|fci(φ1,φ1,ψ1)-fci(φ2,φ2,ψ2)|≤Li‖Φ(t)-Ψ(t)‖,Φ(t)=(φ1,φ1,ψ1)(t),Ψ(t)=(φ2,φ2,ψ2)(t)。因为(0,0,0)≤(φj(t),φj(t),ψj(t))≤(M1,M2,M3),j=1,2,t∈[-τ,0],并且Mi≥ki,所以它是正连续的。
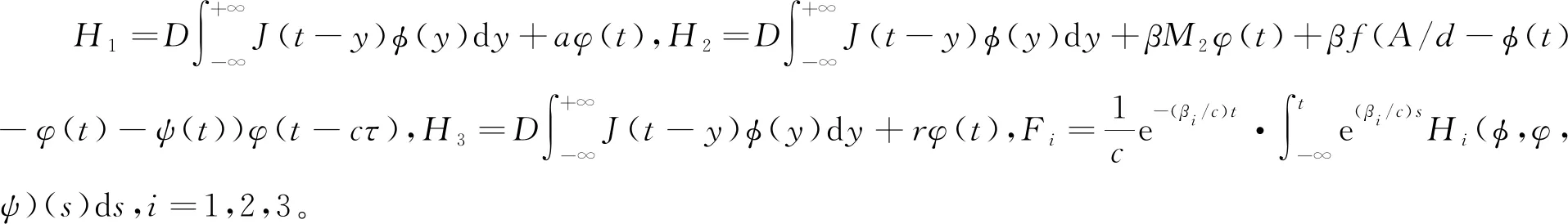
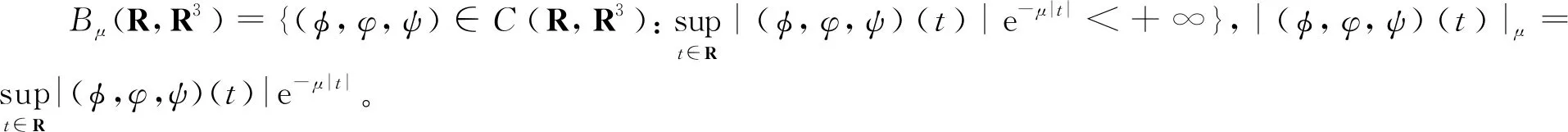
H1(φ,φ,ψ)(t)≥0,H1(φ2,φ2,ψ2)(t)≤H1(φ1,φ1,ψ1)(t),
H2(φ1,φ1,ψ1)(t)≤H2(φ1,φ1,ψ2)(t),H2(φ1,φ2,ψ1)(t)≤H2(φ1,φ1,ψ1)(t),
H2(φ2,φ2,ψ2)(t)≤H2(φ2,φ1,ψ1)(t),H3(φ2,φ2,ψ2)(t)≤H3(φ1,φ1,ψ1)(t),
H3(φ,φ,ψ)(t)≥0,F1(φ2,φ2,ψ2)(t)≤F1(φ1,φ1,ψ1)(t),
F2(φ1,φ1,ψ1)(t)≤F2(φ2,φ1,ψ1)(t),F2(φ1,φ1,ψ1)(t)≤F2(φ1,φ1,ψ2)(t),
F2(φ1,φ2,ψ1)(t)≤F2(φ1,φ1,ψ1)(t),F3(φ2,φ2,ψ2)(t)≤F3(φ1,φ1,ψ1)(t)。
对任意的t∈R,0≤φ2(t)≤φ1(t)≤M1,0≤φ2(t)≤φ1(t)≤M2,0≤ψ2(t)≤ψ1(t)≤M3。通过证明可得以下结论:
引理1[10]假设有(A2)成立,则有F=(F1,F2,F3),在|·|μ范数意义下连续。

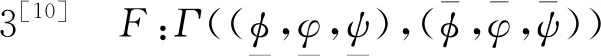
为了构造适当的上下解,分析下面的函数:
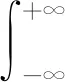
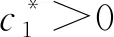
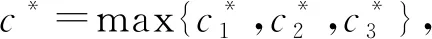
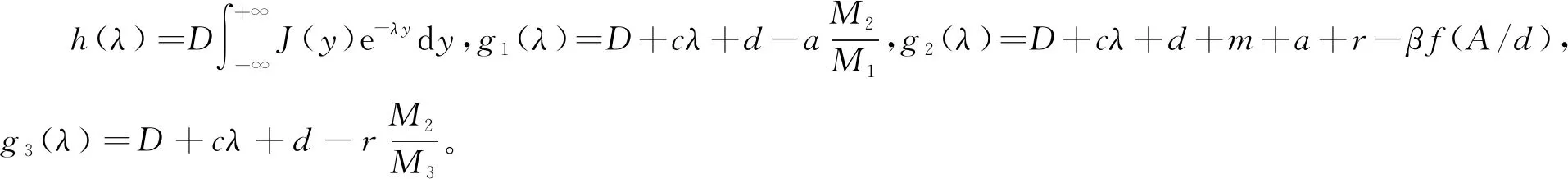
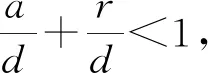
a(k2+ε3)-d(k1+ε1)<0,
βf(A/d-k1+ε2-k2-ε3-k3+ε6) r(k2+ε3)-d(k3+ε5)<0, d(k1-ε2)-a(k2-ε4)<0, r+m+d+a<βf(A/d-k1-ε1-k2+ε4-k3-ε5), d(k3-ε6)-r(k2-ε4)<0, 证明定义 证明定义 本文研究了一类具有非局部扩散的时滞传染病模型,通过构造一对上下解和运用Schauder不动点定理,研究了连接无病平衡点E0(A/d,0,0)和地方平衡点E*=(S*,I*,R*)行波解的存在性。而文献[5]只是研究了系统的稳定性,并没有研究系统的行波解,且没有考虑潜伏期和空间传播对系统的影响。现在研究描述潜伏期的非局部扩散项和时间延迟对波速c*的影响。根据系统(3)的第二个方程,可以得到 cI′(ξ)=D[J*I(ξ)-I(ξ)]+βf(A/d)I(ξ-cτ)-(r+m+a)I(ξ), 通过计算可得 可以看出,对于非局部扩散速率D,波速c*是单调增加的,对于时间延迟τ,波速c*是单调递减的。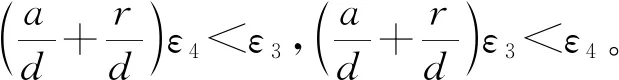
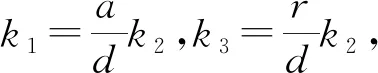

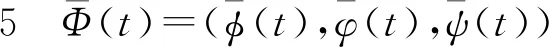

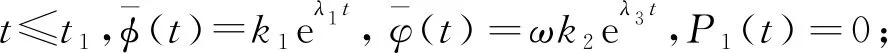
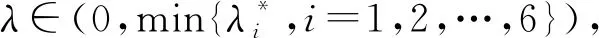
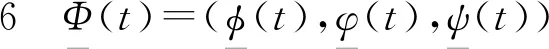
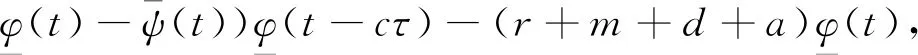
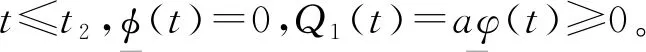
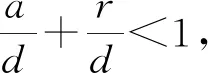
3 结论

