深埋隧道侧穿采空区施工安全距离及能量演化机制

孙飞跃，刘希亮，郭佳奇， 石晓燕， 武文龙， 朱斌忠

(1.河南理工大学 土木工程学院， 河南 焦作 454000； 2.军事科学院国防工程研究院，河南 洛阳 471023)

1 研究背景

近年来，我国经济和科技创新水平大幅提升，使得穿越采空区的山区隧道工程蓬勃发展，诸如毗邻采空区的公路隧道、铁路隧道不断大量涌现，因采空区失稳坍塌导致隧道与采空区之间围岩发生的动力地质灾害，已严重造成施工机械设备的损毁和一线人员的伤亡，并产生了巨大的经济损失[1-6]。因而，隧道与采空区之间的安全距离关系到隧道顺利施工和后期的运营安全，亦成为隧道穿越采空区不良地质段时亟需解决的重大技术难题。

在采空区地段修建隧道所面临的安全稳定性问题受到国内外工程设计、施工和管理人员的高度重视，目前，国内外科研工作者和工程研究人员从力学特征、数值模拟和基础试验方面针对隧道与采空区之间的安全距离开展了大量研究，并就采空区段隧道施工力学特征做了大量的研究工作，取得了卓有成效的研究成果。从20世纪80年代开始，Jonce等[7]、Wang[8]基于经验理论和井下现场调研对采空区、岩溶等引发的地下空洞灾害机理进行了深入研究。Sargand 等[9]、Drumm等[10]系统地研究分析了高速公路下伏采空区对路基变形失稳机理。到20世纪90年代，Soliman等[11]、El-allhas等[12]、Fu等[13]研究了采动覆岩产生离层裂缝的力学条件及离层裂缝的位置。近年来，杨斌[14]深入分析了采空区段隧道施工力学行为，为隧道设计施工提供了科学依据；蒋德武[15]基于围岩屈服强度对采空区段隧道围岩稳定性进行了探究，并对围岩进行了影响分区；童立元等[16]探讨了隧道与下伏采空区间的相互作用机制。在试验研究方面，也取得了重要进展，如：喻洪平等[17]通过井下试验与变形实测数据对隧道侧穿采空区沉降规律进行了分析；胡永占[18]采用InSAR技术对采空区铁路隧道病害成因进行了研究，为隧道病害整治提供了地质参考依据；王飞等[19]以室内试验为研究手段，提出了隧道在采空区影响下的改造方案。随着计算机技术的快速发展，数值模拟方法已成为岩土工程研究和设计的一种主流方法。如：张志沛等[20]运用FLAC3D数值分析软件，分析研究了隧道穿越倾斜采空区的施工力学动态变化特征；崔路允[21]基于强度折减法，利用MIDAS-GTS有限元软件对深埋隧道穿越复杂采空区的施工安全稳定性进行了深入分析；罗春雨[22]以华蓥山隧道工程为依托对隧道侧穿采空区的安全距离进行了研究。

上述研究成果主要聚焦于采空区失稳坍陷对隧道施工力学行为、变形失稳机理和围岩稳定性的影响等问题，但隧道穿越采空区不良地质段时，隧道与采空区间的安全距离是影响隧道稳定和施工运营安全的关键因素，并在一定程度上决定了隧道走线、埋深等设计要求。为了进一步保障采空区段隧道施工安全，以及采空区对隧道施工影响的最小化，有必要对深埋隧道侧穿采空区的施工安全距离及能量演化机制进行研究。鉴于此，本文对有限差分软件FLAC3D进行二次开发，并基于动力数值分析，结合实际工程案例，研究深埋隧道在不同安全距离下的围岩变形特性、应力分布特征以及能量演化机制与动态响应，并且进行了现场数据实测。本研究成果在该领域具有十分重要的工程应用价值并可为类似工程提供参考依据。

2 工程概况

某隧道右洞全长约8 168 m、最大埋深611 m，左洞全长约8 151 m、最大埋深584 m，按双向四车道80 km/h高速公路标准设计，采用分离式双洞布置。在隧道右线K106+280 m～K106+358 m处共有3处采空区，隧址区域岩性以泥岩、泥灰岩、砂质泥岩为主。采空区段围岩稳定性较差，在隧道进口段背斜西翼穿越水巴岩煤矿南端，在出口段背斜东翼穿越田坝煤矿的南端，采空区局部地段顶、底板泥岩厚度较大，岩体裂隙发育，采掘破坏较严重；隧道拱顶处易产生坍塌和不均匀沉降。

3 侧穿采空区深埋隧道施工安全距离数值计算

3.1 建立数值分析模型

(1)数值模型及边界条件。在采用FLAC3D进行求解动力学问题时，为了保证模拟结果的真实可靠，能够真实反映围岩的受力情况，依据圣维南原理和隧洞开挖的影响范围，同时充分考虑采空区地段隧道围岩水文地质条件，以及消除模拟计算所产生的边界效应，建立的计算模型横向长度为100 m、竖向高度为60 m、纵向宽度为50 m。以往研究表明，当地下存在空洞或者采空区时，上覆岩层垮落在工作面两端的岩层上，出现悬挑梁的破坏形式；在竖直方向，由两端逐渐向中部靠拢(断裂带与裂隙带交汇处)形成一个类似圆形的压力拱，在模拟时将采空区简化为圆形空洞，走向与隧道平行，位于隧道右侧，半径为3 m、长度为18 m，数值计算模型见图1、隧道断面尺寸见图2。

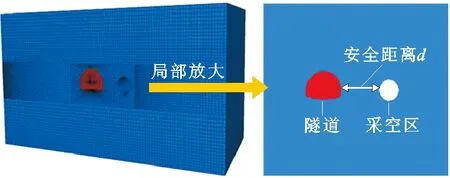
图1 数值计算模型示意图

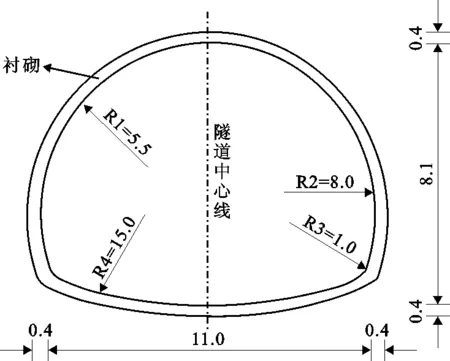
图2 隧道断面尺寸(单位：m)

在动力计算时，为了使系统的动能量快速吸收从而达到收敛，阻尼采用Rayleigh damping、最小临界阻尼比取0.25、最小中心频率取550 Hz；该计算模型的上边界为应力约束边界条件，施加19.62 MPa(现场实测)垂直载荷，计算模型的下边界、前后和左右边界均为位移约束边界条件，模型外围边界设定为静态边界，以减小或消除模拟计算所产生的弹性波反射。

(2)爆破荷载作用形式。由于岩体爆破是一个瞬时产生的复杂过程，爆炸机理及影响因素极其复杂，使爆炸过程的细节很难定量确定。在数值分析中爆破荷载常假定为一个三角形冲击波[23-24]，三角形函数爆炸荷载历程曲线表达式如公式(1)。通过对FLAC3D软件进行二次开发，采用FISH编写程序语言来进行爆破荷载的施加。

(1)

式中:P(t)为任一时刻的爆破荷载压力值,MPa；P0为爆破荷载峰值，MPa；tr为爆破荷载上升至峰值的时间,s；td为爆炸荷载的正压作用的时间,s。

(3)本构模型及力学参数。在数值计算中，本构模型的选取要与工程材料力学特性有很高的契合度，故而模型本构关系采用Mohr-Coulomb屈服准则[25]。围岩与支护结构的力学参数依据该隧区的地质勘察资料及设计资料中的实际物理力学参数选取，如表1所示。

表1 材料的物理力学参数

本模拟对岩石岩性作出假设：岩石为均质、各向同性的连续体，符合Mohr-Coulomb强度准则，材料参数满足Mohr-Coulomb本构模型关系。

3.2 数值分析方案与监测点布置

在数值分析中，隧道与采空区间的安全距离分别取0.25D、0.50D、0.75D、1.00D、1.25D、1.50D(D为隧道跨度，取整数为12 m)，如表2所示。监测点的布置见图3。

表2 数值试验方案

图3 数值分析隧道监测点布置

4 模拟结果分析

4.1 围岩位移场演化过程

各工况隧洞拱顶、拱底、边墙以及围岩的位移变化的数值模拟结果见图4～7。对图4～7进行分析可知：

(1)隧道拱顶、拱底与两侧边墙位移曲线(图4、5)显示，围岩变形量随着隧道与采空区间的安全距离的增大而减小，其变化幅度较为平缓；在隧道拱顶和拱底处，工况6的最大变形量分别为10和9 mm，工况1的最大变形量分别为15和14 mm；在隧道左、右边墙处，隧道围岩两侧边墙位移曲线大致呈对称分布，随着至隧道中心距离的增加围岩两侧边墙的位移变形量逐渐减小，距隧道中心距离越近围岩变形越大，表明隧道洞口受爆炸冲击响应最明显。

图4 各工况隧道拱顶和拱底位移变化曲线

(2)竖向位移等值线云图(图6)显示，竖向位移的峰值主要集中在隧道拱顶和拱底处，拱顶变形量为负代表下沉，拱底变形量为正代表隆起。在隧道较为靠近采空区时(工况1～3)，围岩变形受采空区影响最为显著，变形范围和增加幅度明显大于其他工况，且有明显的不对称变形倾向，并表现出向采空区一侧扩大的趋势；工况4～6中围岩变形范围与变形幅度较为平缓，受采空区的影响可以忽略。故对于隧道围岩竖向位移，安全距离为1D(即12 m)以内的采空区会加大隧道围岩的沉降程度和范围，给隧道建设带来不利的影响。

图5 各工况隧道两侧边墙位移变化曲线

图6 各工况竖向位移等值线云图

(3)水平位移等值线云图(图7)显示，隧道两侧受围岩挤压作用均向隧道内部发生移动，且两侧变形大致对称，并呈蝴蝶状分布。在隧道较为靠近采空区时(工况1～3)，因采空区的存在劣化了围岩性质，围岩的侧向约束能力有所降低，致使隧道右侧的水平位移明显大于其他工况，向内变形程度较大。在距离采空区最近的工况1中，隧道右侧边墙的位移反而比距离较远的工况2和3小，表明采空区左侧因隧道爆破开挖扰动而产生较大的向内变形，在距离过近时，其变形通过隧道与采空区间的岩柱传递到隧道右侧，导致隧道右侧向右变形趋势增强，在数值上表现为隧道右侧的一部分向左变形的值被抵消。此时采空区空腔的变形已严重影响了隧道施工，对隧道结构最为不利。故对于隧道围岩水平位移，安全距离为1D(即12 m)以内的采空区会产生明显的不利影响，对隧道右拱腰尤为明显；安全距离为0.67D(即8 m)以内的采空区对隧道的影响较大，导致隧道与采空区之间的围岩发生局部畸变(图8)。

图7 各工况水平位移等值线云图

隧道结构变形畸变区示意图如图8所示。为更好地探究隧道结构在采空区影响下所产生的不对称变形(畸变)，现提取出工况2的隧道结构变形及位移矢量(放大系数为140)，如图9所示。

图8 隧道结构变形畸变区示意 图9 工况2隧道围岩位移矢量分布

采空区与隧道之间是相互影响的，隧道右侧与采空区左侧均产生了较大侧向位移，即隧道净空和采空区空腔变形收敛，中间岩柱两侧受拉，受力环境十分恶劣，围岩较为松动。为进一步研究该处隧道的变形情况，绘制出各工况下4个监测点的位移变化曲线，见图10。由图10可知，工况1和2在采空区分布区域均有明显向采空区一侧发生正向位移突变，这是由于隧道爆破开挖后形成临空面，围岩自稳能力降低，整体强度下降，导致采空区左侧向内变形速率增加；在工况3和4中，由于隧道与采空区距离不远，采空区空腔导致的位移增加幅度较为缓和，但此时采空区对隧道结构的影响仍不可忽视；在工况5和6中，由于隧道与采空区距离较远，监测点的位移变化不明显，此时采空区对隧道结构的影响可忽略不计。

图10 各工况4个监测点的位移变化曲线

综上所述，工况1～2中采空区对隧道影响十分严重，并会导致隧道发生局部畸变；工况3～4中采空区对隧道影响较小，但其位移增幅效应仍不可忽视；工况5～6中可认为采空区对隧道已无影响。

4.2 围岩应力场演化过程

各工况隧洞拱顶、拱底、边墙以及围岩的应力变化的数值模拟结果见图11～14。对图11～14进行分析可知：

(1)隧道拱顶、拱底与两侧边墙应力曲线(图11、12)显示，工况1的拱顶、拱底应力值明显大于其他工况，随着安全距离的加大，应力值迅速减小，其中工况1～3的减小速率最大，在拱顶处从8.4 MPa减小至7.3 MPa、在拱底处从8.6 MPa减小至7.6 MPa，受距离影响明显；工况4～6的拱顶、拱底应力值变化幅度极小，此时可认为采空区对隧道的影响可忽略不计。隧道围岩左右两侧的应力曲线大致呈对称分布，两侧水平应力对隧道影响较大的范围大致距离隧道中线左右两侧12 m处，离隧道中线越远处变化越不明显，并且逐渐趋近于围岩的原岩应力。

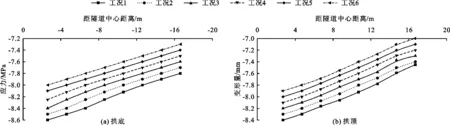
图11 各工况隧道拱顶、拱底应力变化曲线

(2)竖向应力等值线云图(图13)显示，应力值为负表明隧道处于受压状态；隧道受爆破开挖的影响，其周围围岩应力将进行重新调整。距隧道中心距离越近，应力变化越明显，随着距离的增加，应力增长速率较为平缓，逐渐趋近于原岩应力；在相同应力水平下隧道拱顶应力影响范围比拱底大，拱顶处发生应力集中现象，在隧道表面处应力释放的范围增大。工况1～3有明显的应力集中现象，主要分布在隧道的拱顶、拱底以及两侧与底板交接处；在工况4～6中随着采空区与隧道右侧距离的增加，应力集中现象逐渐减弱。

图13 各工况竖向应力等值线云图

(3)水平应力等值线云图(图14)显示，由于隧道两侧水平应力的影响区域比顶板和底板多，从而导致隧道两侧水平应力分布呈现不规则形态，整体近似为椭圆状分布。随着隧道与采空区间的安全距离的增加，围岩水平应力等值线云图作用范围增大，从而说明选择最佳的安全距离对洞室开挖有一定的影响。在工况1～6中，虽然随着安全距离的增大，围岩应力有所增大，但增加幅度不大。

图14 各工况水平应力等值线云图

综上所述，从采空区对隧道结构的应力变化水平来看，安全距离为1D(即12 m)以内的采空区会造成隧道右侧出现应力集中现象，同时应力值也会增大，给隧道施工安全带来隐患，在施工设计时应引起重视。

图12 各工况隧道两侧边墙应力变化曲线

4.3 能量演化过程

(1)能量释放规律研究。各工况隧道周边围岩弹性应变能密度分布状态见图15；各工况4个监测点处弹性应变能随时间变化见图16。分析图15～16可知，隧道在爆破开挖以后，洞室周边围岩由三向受力状态转为两向受力状态，在应力集中作用下，隧道围岩向开挖掌子面转移，内部围岩应力场将重新分布，形成二次应力场。围岩弹性应变能随安全距离的增加而增大，但增长幅度较小；工况1～3在洞室拱顶、拱底、边墙及边角处弹性应变能最大，导致掌子面前方聚积较多的弹性能，若这些能量迅速释放，岩体将产生爆裂、松脱、剥离、弹射、抛掷等破坏现象的动力失稳地质灾害。随着安全距离的增加，工况4～6中掌子面前方聚积的弹性能较少。

图15 各工况隧道周边围岩弹性应变能密度分布状态

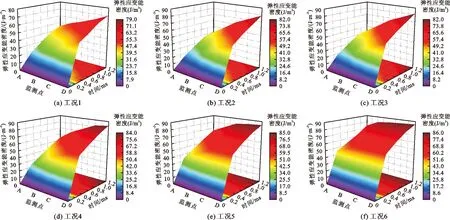
图16 各工况4个监测点处弹性应变能密度随时间的变化

(2)能量转化规律研究。为了探讨爆破荷载作用下围岩能量转化与应力比(应力水平上限值σmax与峰值应力σp之比)变化的相关性，拟合出了不同安全距离下隧道围岩累积水平能量与应力比的关系曲线，如图17所示。由图17分析可知，不同安全距离下，累积水平能量与应力比的曲线变化趋势大致相同。在工况1～6中，同应力水平下，应力比随着安全距离的增大而降低，相应的累积水平总能量和弹性应变能减少，但耗散能随着安全距离的增大先减少后增加；同应力比下，累积总能量和弹性应变能随着安全距离的增加而增大，增加幅度较高；随着应力比的增加，累积水平总能量、弹性应变能和耗散能呈现出下凹型增长趋势。

图17 各工况隧道围岩累积水平能量与应力比的关系曲线

(3)能量分配规律研究。为了便于形象展示隧道与采空区在不同安全距离下的能量分配，绘制出弹性应变能比例n(累积水平弹性应变能与累积水平总能量之比)、耗散能比例m(累积水平耗散能与累积水平总能量之比)和耗散能比例系数e(累积水平耗散能与累积水平弹性应变能之比)与应力比的关系曲线，如图18所示。

由图18可知，不同工况下，n、m、e的曲线变化趋势均一致。随着安全距离的增加，n首先逐渐增加而后趋于稳定趋势，直至爆破开挖后应力水平曲线骤降，曲线大致呈倒U型分布；m、e首先降低而后也趋于稳定，最后曲线瞬间升高，大致呈U型分布。n、m、e不仅可直接反映围岩在各应力水平下的能量分配比例，而且还能间接反映隧道围岩内部损伤程度和能量转化机制。

图18 各工况隧道围岩弹性应变能比例、耗散能比例及耗散能比例系数与应力比的关系曲线

由图18可知：

(1)工况1～2中，n、m减少幅度最大，e增加幅度最大。

(2)工况3～4中，应力比分别为0.38～0.57、0.61～0.82时，n、m、e处于较为稳定趋势。

(3)工况5～6中，随着安全距离的增加，n、m、e曲线变化与其他工况相比增长幅度较为平缓。

总之，工况1～2达到能量弱化阶段的应力比速率较低而达到强化阶段的应力比速率较高。

5 工程应用分析

在隧道施工中，采空区与隧道之间的合理安全距离在一定程度上决定了隧道走线、埋深、长度等设计因素，鉴于围岩水文地质条件和施工环境的复杂性以及后期运营安全，需对现场施工进行跟踪监测，并进一步根据反馈数据进行及时调整，以提高隧道施工运营安全。在前节数值试验结果的基础上，选取工况4(安全距离为1D)K106+318 m处的测点进行爆破监测，使得采空区与隧道之间的振动速度控制在国家安全标准范围以内，从而避免采空区失稳坍塌，使施工顺利安全进行。现场测点位置布置见图3，A、B、C、D 4个测点X、Y、Z3个方向振速实测结果如图19所示。

一次爆破振动测试能同时采集空间上3个方位的振动速度分量。时程图谱中，X、Y、Z3个通道采集的速度时程曲线，分别对应了水平切向(与边墙相切且沿隧道线路走向方向)、竖直方向(与边墙相切且垂直于地面的方向)和水平径向(与边墙垂直的方向)这3个方向。

分析时程图谱可知：

(1)爆破振动总时长约为1 s，3个方向上的振动速度时程曲线均有7个明显波段，且3个方向上各波段的出现时间和结束时间大致相同。

(2)测点最大爆破振动速度一般发生在掏槽爆破时(图中峰值发生在第1次掏槽爆破时)。因此，若隧道需要进行控制爆破振动，则重点要放在掏槽孔减震上。

(3)测点合振振动速度的峰值为12.59 cm/s，小于国家《爆破安全规程》(GB 6722—2014)[26]中规定的交通隧道爆破安全允许振动速度，即质点振动速度不得超过12～15 cm/s。这表明在当前爆破设计下，安全距离为1D时采空区对隧道的稳定性影响有限，隧道侧穿采空区地段施工整体上稳定且符合安全需求。

图19 4个测点X、Y、Z 3个方向的振速实测曲线

6 结 论

本文针对隧道侧穿采空区所面临的工程问题，通过FISH语言编程对FLAC3D数值模拟软件进行二次开发，并结合工程现场实测对深埋隧道侧穿采空区施工安全距离及能量演化机制进行研究，得到了如下结论：

(1)围岩位移场演化规律表明，工况1～2中采空区对隧道影响十分严重，并会导致隧道发生局部畸变；工况3～4中采空区对隧道影响较小，但其位移增幅效应仍不可忽视；工况5～6中可认为采空区对隧道的影响可忽略不计。

(2)围岩应力场演化规律表明，工况1～3有明显的应力集中现象，主要分布在隧道的拱顶、拱底以及两侧与底板交接处；工况4～6中随着采空区与隧道右侧距离的增加，应力集中现象逐渐减弱。

(3)能量演化规律表明，工况1～2中，n、m减小幅度最大，e增加幅度最大；工况3～4中，应力比分别为0.38～0.57、0.61～0.82时，n、m、e处于较为稳定趋势；工况5～6中，随着安全距离的增加，n、m、e曲线变化与其他工况相比增长幅度较为平缓。累积应力水平能量和应力比之间的曲线可分为加速、均速和减速3个阶段，3个阶段的能量演化亦能较好地反映围岩内部损伤破坏机制。

(4)结合工程现场振速实测曲线，振动速度的峰值分别为14.26和12.59 cm/s，小于国家《爆破安全规程》(GB 6722—2014)中规定的交通隧道爆破安全允许振动速度，即质点振动速度不得超过12～15 cm/s。这表明在当前爆破设计下，安全距离为1D时采空区对隧道的稳定性影响有限，隧道侧穿采空区地段施工整体上稳定且符合安全需求。

(5)综合考虑以上各种因素得出隧道侧穿采空区的安全距离规律，采空区距隧道0.5D(6 m)以内时，采空区对隧道结构有重大影响，隧道结构处于危险区；采空区距隧道0.5D～1D(6～12 m)之间时，采空区对隧道结构的影响不可忽略，隧道结构处于影响区；采空区距隧道大于1D时，采空区对隧道结构的影响可忽略不计，隧道结构处于安全区。