输电线路故障测距方法研究

彭丹阳 何艺萌 李丁 张铭飞 白苏赫

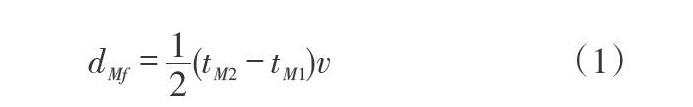
摘 要：随着信号处理技术的不断发展，行波法在输电线路故障测距方面取得了较大进步。本文综合现有行波测距法，分析不同行波故障定位方法的优缺点并进行比较。结果表明：多端行波测距方法误差远小于单端、双端行波测距法，双端行波测距法误差小于单端行波测距法。

关键词：故障定位;行波法;单端行波测距;双端行波测距;多端行波测距

中图分类号：TM755文献标识码：A文章编号：1003-5168（2021）10-0027-03

Research on Fault Location Method of Transmission Line

—Taking Traveling Wave Ranging Method as an Example

PENG Danyang HE Yimeng LI Ding ZHANG Mingfei BAI Suhe

（North China University of Water Resources and Electric Power，Zhengzhou Henan 450000）

Abstract： With the continuous development of signal processing technology， traveling wave method has made great progress in fault location of transmission lines. In this paper， the advantages and disadvantages of different traveling wave fault location methods were analyzed and compared. The results show that the error of multi terminal traveling wave ranging method is far less than that of single terminal and double terminal traveling wave ranging method， and the error of double terminal traveling wave ranging method is less than that of single terminal traveling wave ranging method.

Keywords： fault location;traveling wave method;single terminal traveling wave location;double terminal traveling wave location;multi terminal traveling wave location

输电线路承担着电力传输的重任，其可靠性决定着整个电网的安全运行。当某段线路突发故障后，迅速且精准地进行故障定位，进而尽快消除故障，是保障输电线路稳定运行的重中之重。当前，输电线路故障点检测方法主要包括单端行波测距法、双端行波测距法和多端行波测距法[1-6]。这三种方法无论是在设备成本上还是基本原理上都存在显著差异。

1 行波测距方法与原理

1.1 单端行波测距

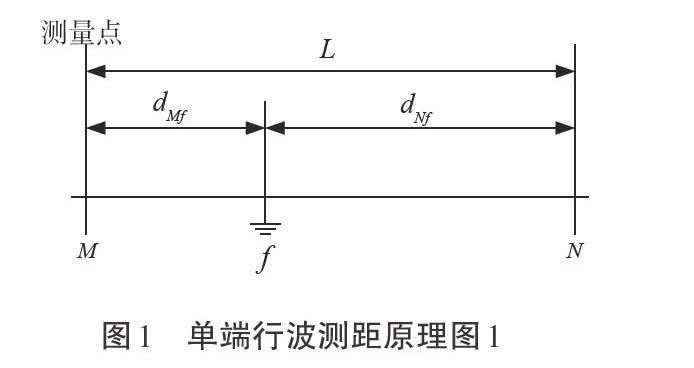
1.1.1 单端行波测距原理。①故障发生距离小于线路总长的一半。当输电线路上的故障距离小于线路总长度的一半时，所测得的第二个行波的波头应是来自故障点的反射波。单端行波测距原理图如图1所示，故障距离[dMf]的计算公式如式（1）所示。

[dMf=12（tM2-tM1）v]                          （1）

式中：[v]表示行波传播速度，m/s;[tM1]表示故障行波到达点M的时间，s;[tM2]表示经故障点反射波到点M的时间，s。

②故障发生距离大于总线路长度的一半。故障发生位置超过线路总长度的一半时，第二个故障行波的波头是对侧母线的反射。单端行波测距原理如图2所示，故障距离[dMf]的计算公式如式（2）所示。

[dMf=L-12（tM2-tM1）v]                        （2）

1.1.2 單端行波测距的特点。单端行波测距法，成本相对较低，无须依赖定位系统和数据通信等设备即可完成检测分析[7]，并且具有较好的实时性。但其缺点也是显而易见的，计算前需要先判断故障的发生位置与线路总长度的关系。

1.2 双端行波测距

1.2.1 双端行波测距原理。双端行波故障测距是通过行波的传播速度、故障初始行波到达线路两端测量点的时间差和输电线路的长度来确定故障点。双端行波测距原理如图3所示，故障距离[dMf]和[ dNf]的计算公式如式（3）和式（4）所示。

[dMf=12tM-tNv+L]                      （3）

[ dNf=12tN-tMv+L  ]                    （4）

式（3）和式（4）中：[v]表示行波传播速度，m/s;[tM]表示N故障行波到达点M的时间，s;[tN]表示故障行波到达点的时间，s。

1.2.2 双端行波测距特点分析。双端行波测距法避免了单端行波测距法中存在的难点，通过线路两端的装置，得到行波到达测量点的时间，并达到较高定位精度[8]。但双端法的成本相对偏高，涉及两端数据通信等[9]。

1.3 多端行波测距

1.3.1 多端行波测距原理。多端行波测距原理如图4所示。故障行波到达测量端（简称测量点1、测量点2、测量点3）的时间分别为[tM]、[tQ]、[tN]。

故障距离[dMf]可表示为：假设在线路[LNQ]和[LMQ]上的行波传播速度为[vNQ≈ vMQ= v]，则得出的计算公式如式（5）所示：

[tN-t0v=dNf′tQ-t0v=dQf′            （tM-t0）v=LMQ′+dQf′   dNf′+dQf′=LQN′]                     （5）

式中：[LMQ′]、[LQN′]表示故障行波传播所经过的路径，m;[dNf′]、[dQf′]为故障点分别与测量点1以及测量点2的物理长度，m;[tM]、[tQ]、[tN]为故障行波到达测量点1、测点2、测点3的时间，s。

在线路杆塔挡距和弧垂相近的情况下，均可认为是现场线路长度数据放大一定系数[ε]后的数值，即计算公式如式（6）所示：

[tN-t0v=εdNftQ-t0v=εdQftM-t0v=εLMQ+εdQfεdNf+εdQf=εLQNdNf=tN-tMLMQ2tM-tQ+L2]                   （6）

式中：[LMQ]、[LQN]为线路杆塔距离之和得到的现场线路长度，m;[dNf]、[dQf]分别为故障点到测量点1以及测量点2的现场线路长度，m。

1.3.2 多端行波测距特点分析。多端行波测距法不用测量行波在不同参数线路上的传播速度。利用该方法计算故障距离，当杆塔距离和弧垂相近时，一定程度上消除了线路弧垂对测距精度的影响。

2 仿真分析

2.1 仿真模型搭建

利用MATLAB中的电力系统工具箱建立线路长度为300 km、电压等级110 kV的双电源供电系统进行仿真分析。故障距离设置为120 km，故障时间为0.024 s发生A相短路接地，故障采样频率为50 000 Hz。电力系统仿真模型如图5所示。

在此输电线下，行波波速[v=2.956  553  97×108] m/s。

2.1.1 单端行波测距仿真。对模型进行仿真分析，首先，得到首端测量点的故障电流行波波形;其次，对所得波形进行相模变换;再次，进行db5小波分析以及模极大值分析。波形到达时间为0.024 48 s以及经故障点反射后到达母线的时间为0.025 34 s。两行波波头时间差值为0.000 86 s，根据公式（1）可得故障点距离127.131 km，误差大小为2.38%。

2.1.2 双端行波测距仿真。行波到达首端母线时间与单端行波测距中的时间一致，因此，只需对故障行波到达对侧母线时间进行分析。

行波到达首端母线时间为0.024 48 s，故障行波到达对端母线时间点即为原始信号首次波形突变点。根据模极大值分析可知，到达对侧母线的时间为0.024 7 s。首端与对端母线时间差值为0.000 22 s，根据公式（3）可得故障距离为117.478 km，误差大小为0.840%。

2.1.3 多端行波测距仿真。行波到達两端母线时间与单端、双端一致，对故障行波到达中间测量点进行分析。故障行波到达首端时间0.024 48 s，故障行波到达测量点2的时间点中原始信号首次突变点，对应时间点0.024 12 s和故障行波到达对侧母线时间点0.024 7 s。根据公式（6）计算可得故障距离为121.552 km，误差大小为0.517%。

2.2 仿真结果分析

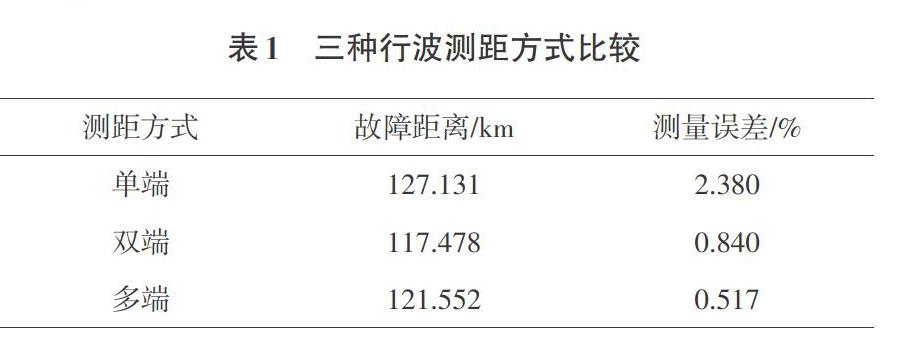
通过分别对单端、双端以及多端行波测距进行仿真模拟，得出多端行波测距精确度要优于单端行波测距精度以及双端行波测距精度，而单端行波测距精度要略低于双端行波测距精度。表1为多种行波测距方式误差比较。

3 结语

经过本文的比较分析可知，多端行波测距在故障定位中具有更好的精度，而单端行波测距精度要略低于双端行波测距精度。现有的测距算法各有其优缺点，都有需要进一步解决的技术问题。

参考文献：

[1]徐丙垠. 现代行波测距技术及其应用[J].电力系统自动化，2001（23）：62-65.

[2]刘万超，陈平，孙佳佳，等.基于数学形态学的输电线路单端行波故障测距研究[J].电网与清洁能源，2009（4）：29-33.

[3]覃剑，葛维春，邱金辉，等.输电线路单端行波测距法和双端行波测距法的对比[J].电力系统自动化，2006（6）：92-95.

[4]张峰，梁军，张利，等.基于三端行波测量数据的输电线路故障测距新方法[J].电力系统自动化，2008（8）：69-72.

[5]朱永利，范新桥，尹金良.基于三点电流测量的输电线路行波故障定位新方法[J].电工技术学报，2012（3）：260-268.

[6]艾颖梅，陈剑云，何军娜，等.基于三端法的HHT行波故障测距研究[J].电测与仪表，2015（21）：11-16.

[7]崔惠伟，杨锋，张意，等.单端行波法应用于输电线路故障测距的研究[J].江西电力，2007（6）：1-3.

[8]全玉生，张煜，邱庆春，等.基于GPS的双端故障定位新算法[J].电网技术，2004（6）：63-66.

[9]吴欣荣，罗承沐，苏进喜，等.基于单端电气量的故障定位算法研究[J].中国电力，2000（6）：48-50.