基于模型预测的阻尼与车身高度协同控制

于文浩, 周 蓥

(江苏大学 汽车与交通工程学院， 江苏 镇江 212013)

空气悬架具有变刚度、低振动频率等优点，能够提升车辆的行驶平顺性、操纵稳定性和道路友好性.同时空气悬架独有的便捷车身高度调节也能够极大缓解在不同工况下车辆操纵稳定性和乘坐舒适性的矛盾.随着悬架技术的不断发展，空气悬架系统中的可控结构也逐渐增多，除车身高度控制外，可调阻尼减振器也逐渐被更多的空气悬架系统所采纳.

对于可调阻尼减振器，目前国内外研究的控制方法众多，如天棚、地棚、混合天地棚、LQR(linear qua-dratic regulator)控制、滑模控制和模糊控制等[1-3].而对于车身高度控制，国内外研究[1-4]已经从经典控制领域，如PID(proportional integral derivative)控制、积分分离的PID控制等向多模式切换控制、混杂控制、滑模控制及神经网络PID自适应控制等现代控制领域发展.现有研究表明[2-5]不论是可调阻尼减振器或车身高度调节皆可通过相应的控制独立提升悬架性能，以满足各自所面对的性能需求.

随着空气悬架上各可控结构控制研究逐渐成熟，如何充分协调阻尼与车身高度控制，在相互协同的基础上达到整体性能的更优，逐渐成为国内外的研究热点.在诸多协同控制研究中，汪少华等[4]提出基于车身高度切换优先的车身高度和阻尼多模式切换控制，并仿真验证模式切换控制系统的有效性.CHEN Y. K.等[5]根据车速和路面不平度确定车身高度，从阻尼与空气弹簧刚度相匹配的角度出发，协同车身高度与阻尼.赵景波等[6]提出一种主动悬架系统高度与阻尼集成控制方法，并通过试验验证了不同车身高度和不同阻尼形式的组合对车辆性能的影响.可见当前的车身高度与阻尼的协同大多停留在不同车身高度下阻尼的切换与匹配阶段，尚未进行较深入的探索[7].

针对车身高度与阻尼协同控制方面研究的不足，笔者基于模型预测控制理论，以整车综合评价指标为成本函数，当前状态下车身高度与可调阻尼减振器所能生成的悬架力为约束设计模型预测控制器，通过将模型预测问题转化为最优二次型问题求解当前状态下整车最优悬架力.根据当前状态下悬架动行程的导数求解理论所需的阻尼系数，并限幅至实际可控阻尼系数范围作为最终阻尼系数，并依此计算最终的阻尼力.以最优悬架力和阻尼力差值作为车身高度所应生成的弹簧力，利用现有的线性化充、放气模型，求解各充、放气电磁阀开关时长，并通过仿真与实车试验验证所提的协同控制策略的有效性.

1 空气悬架整车动力学建模

根据悬架研究需求，将整车模型适当简化为7个自由度：4个车轮簧下质量的垂向振动以及簧上质量的侧倾、俯仰和垂向振动.根据前期研究，经试验验证简化后的整车模型示意如图1所示,mb为簧上质量；Zb为簧上质量质心位置处的垂向位移；Fi、Fsi、Fdi和fdi分别为车辆i位置处的悬架力、空气弹簧力、阻尼力和悬架动行程，i分别为前左(fl)、前右(fr)、后左(rl)、后右(rr)车轮；fdi为悬架的动行程；Ir和θ分别为簧上质量绕x轴的侧倾转动惯量和簧上质量侧倾角；Ip和φ分别为簧上质量绕y轴的俯仰转动惯量和簧上质量俯仰角；lf和lr分别为前、后轴到质心的距离；Bf和Br分别为前、后轴车轮的左右轮距；mti为车辆四轮位置处的簧下质量；Zti为各簧下质量的垂向位移；Kt为车轮的垂向刚度；qi为四轮位置处的路面垂向激励;Sei为各空气弹簧的有效面积.

图1 自由度整车模型示意图

根据车辆动力学，该7自由度整车模型[8]为

(1)

(2)

上述模型中，悬架力Fi由空气弹簧及阻尼器生成，其中空气弹簧具有显著的非线性特性，这使得控制器的设计更加复杂，同时运算效率大大降低.为满足悬架控制的高实时性要求，将空气弹簧模型线性化，利用线性控制方法来解决阻尼与车身高度的协同控制问题.根据文献[9]，当车身高度电磁阀关闭时，整车线性状态空间方程可写作

(3)

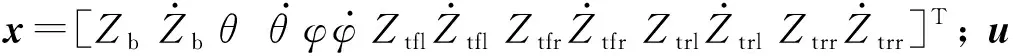
当车身高度调节电磁阀打开时，根据文献[10]，因车身高度引起的空气弹簧内气压变化，可写为

(4)

2 模型预测控制器设计与仿真

2.1 成本与约束

W=CdWx[k]+DduWu[k]+DdωWω[k]，

(5)

式中：CdW∈R12×14、DduW∈R12×4、DdωW∈R12×4为状态矩阵；k为采样周期.

除上述控制目标外，实现目标的控制成本常常也被纳入考量以限制系统的能量消耗.因此整个MPC控制器的成本函数可写为

uT[i]RWu[i]),

(6)

式中：n为预测时域；P为终端状态权重矩阵，对于本系统，其终端状态x[n] 设置为零向量，因此矩阵P项可忽略；

(7)

RW=ρuI4,

(8)

式中：ρu为控制量u的权重系数.

将式(5)代入式(6)并化简，可得到MPC控制器成本函数的标准形式：

uT[i]Ru[i]+2xT[i]Nu[i]}，

(9)

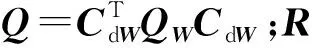
在实际系统中，空气悬架系统可产生的悬架力存在一定限制，因此还应在MPC控制器设计中将此限制以约束的形式考虑进去，保证求解的最优控制量在悬架能力范围内.

本研究设计的MPC控制器的控制量u为悬架力，而最终的悬架力F将由可调阻尼减振器产生的可调节阻尼力FD和车身高度控制改变的空气弹簧力FH组成，即

F=FD+FH，

(10)

其中各部件产生的力都存在一定的约束.

对于单个可调阻尼减振器而言，其阻尼力Fdamper与簧上、簧下质量的相对速度有关,即

(11)

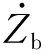
若c∈[c1，c2]，c1、c2分别为阻尼器可调节的最小、最大阻尼系数.则对于整个可调阻尼减振器而言，阻尼力Fdamper的约束为

(12)

若将系统的阻尼看作不可控部分c1和可控部分[0，c2-c1]的组合，则对整车而言，各可调阻尼减振器可控部分阻尼力FD的约束为

(13)

车身高度控制是通过管路对空气弹簧进行充放气操作达成的，在车身高度控制过程中，由于高压罐相对于充入空气弹簧的气体而言体积较大，因此常把高压罐气压认为是固定值以简化计算，同时空气弹簧放气时下游大气压也作为固定值.则离散后的车身高度系统对空气弹簧充放气时的质量流率可表示为

(14)

则车身高度调节引起的各空气弹簧力的变化范围为

ΔpHdi[k]S0i≤FHi≤ΔpHci[k]S0i,

(15)

式中： ΔpHdi[k]、ΔpHci[k]分别为在k时刻因充气和放气引起的第i个空气弹簧气压变化值；S0i为第i个空气弹簧的初始有效面积.

与阻尼约束不同的是，车身高度部分的约束与系统状态量间的逻辑关系无关而只与状态量的值有关.联合上述两者约束，则整车控制量u的约束可表示为两者的交集.

上述优化问题可以转化为QP(quadratic program)问题并可采用积极集法和内点法等最典型的方法求解，通常直接通过MATLAB求解.

2.2 阻尼与车高的动作求解

上节已构建MPC控制器，通过求解成本函数的最小值获得当前整车状态下最优悬架力.但对应到空气悬架系统中，悬架力的可控部分则是由可调阻尼减振器和车身高度控制系统共同作用的结果，而该2个可控结构的具体动作并未通过MPC求解，本节将根据MPC协同控制器输出最优悬架力，确定阻尼器及充放气电磁阀的具体动作.

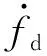
(16)

由于阻尼减振器的阻尼系数可调节部分实际范围为[0，c2-c1]，则实际阻尼器的最优阻尼系数c*与阻尼力FD为

(17)

(18)

此时需要车身高度控制系统利用空气弹簧提供FH=F-FD的悬架力.若当前空气弹簧内气压为p，则车身高度需改变空气弹簧内气压幅值为

(19)

当充气或放气电磁阀开启时，可利用式(4)求得此时各充放气管路内的气体质量流率.考虑到现今SMC的SX10型号电磁阀开闭频率已高达1.2 kHz，因此以采样周期THs=0.001 s对式(4)进行离散化，获得各电磁阀开启0.001 s后各空气弹簧的气体质量与气压变化，有

(20)

(21)

考虑到MPC控制器采样间隔为0.01 s，因此每隔0.01 s控制器就会生成新的最优悬架力，所以根据式(21)计算后，ti限幅至满足ti∈[0, 0.01]s.

2.3 MPC控制器仿真效果分析

为验证控制及算法有效性，在C级路面以车速72 km·h-1为行驶工况进行仿真.路面激励与MPC控制器输出的最优悬架力如图2所示，其中t为时间.

图2 路面激励与MPC控制器输出的最优悬架力

根据当前车辆状态，结合图2最优悬架力和2.2节中阻尼与车高的动作求解方法，可计算出可调阻尼减振器和车高控制器所应产生的悬架力.

仿真前1 s的可调阻尼减振器、车身高度控制器的表现分别如图3、4所示.

图3 可调阻尼减振器表现

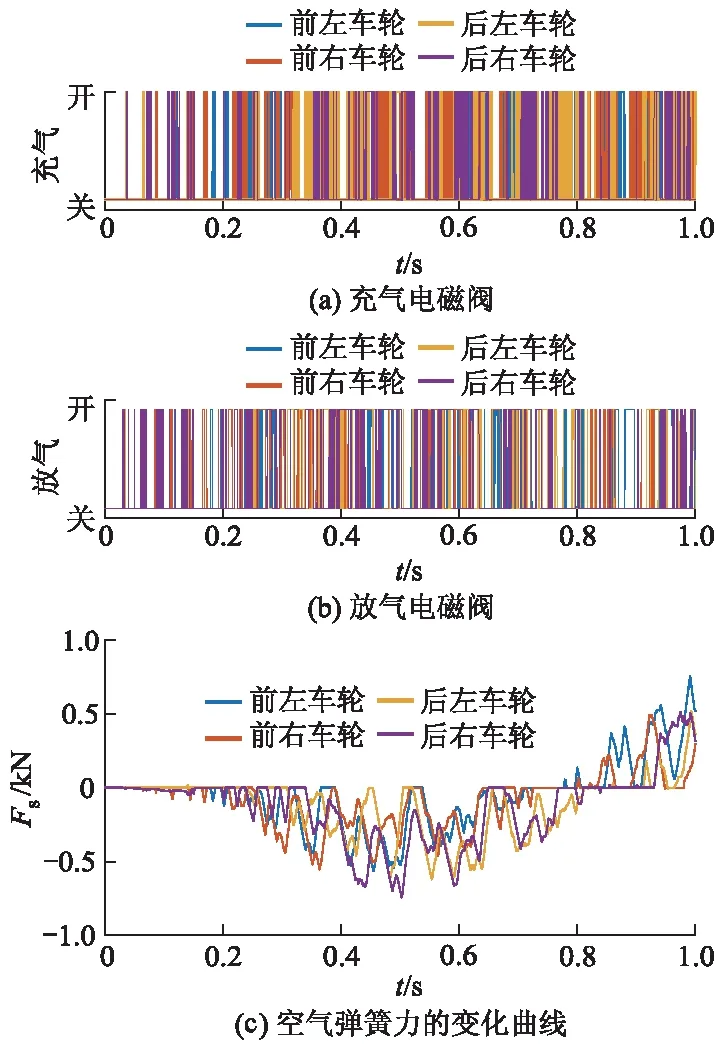
图4 车身高度控制器表现

阻尼器仅能产生正比于悬架动行程导数的力，在悬架动行程导数为0时，阻尼器产生的力为0，因此，阻尼力时常跌落至0(见图3).对车身高度控制器而言，在各采样时刻，通过电磁阀的开闭为空气弹簧充放气，利用空气弹簧配合阻尼器生成所需最优悬架力.从图2-4可明显看出阻尼与车身高度控制系统的配合关系，表明所提控制策略切实可行.

在确定控制策略的可行性后，再次通过仿真分析对比在空气悬架系统中采用协同控制与非协同控制时的性能差异.在空气悬架系统非协同控制中，可调阻尼减振器采用经典的天棚控制策略，4个阻尼器根据其位置处的簧上、簧下质量速度独立运行；车高调节控制器采用PID-PWM控制策略，同时设置其目标为保持车身高度为0.在车速分别为36、72、108 km·h-1时，协同控制与非协同控制的性能对比如图5-7所示.其中：RMS1为簧上质量加速度均方根值；RMS2为轮胎动载荷均方根值；η为降低率.

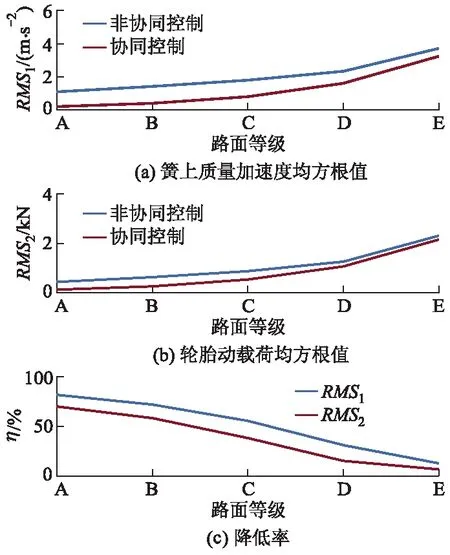
图5 车速为36 km·h-1时2种控制的性能对比

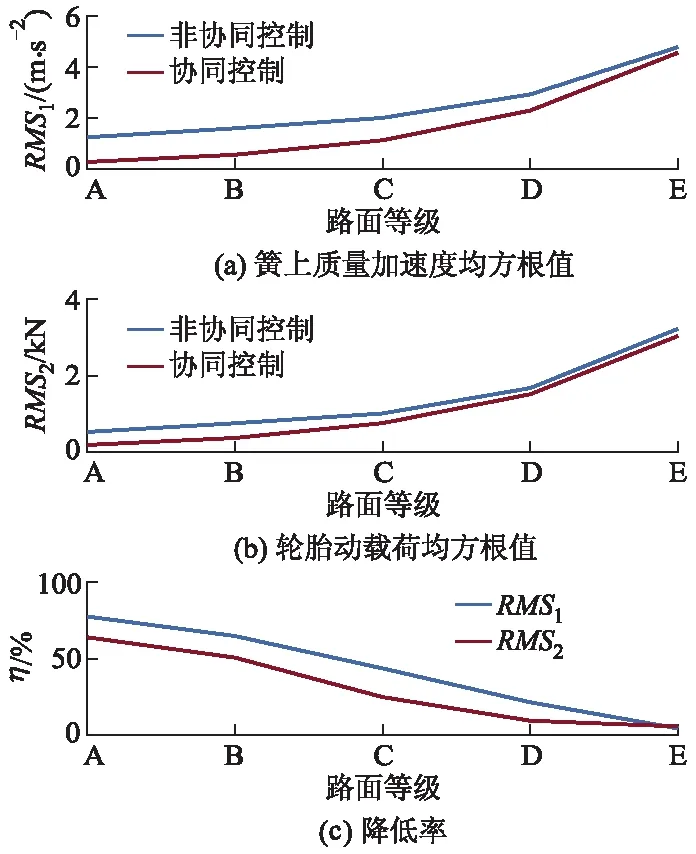
图6 车速为72 km·h-1时2种控制的性能对比

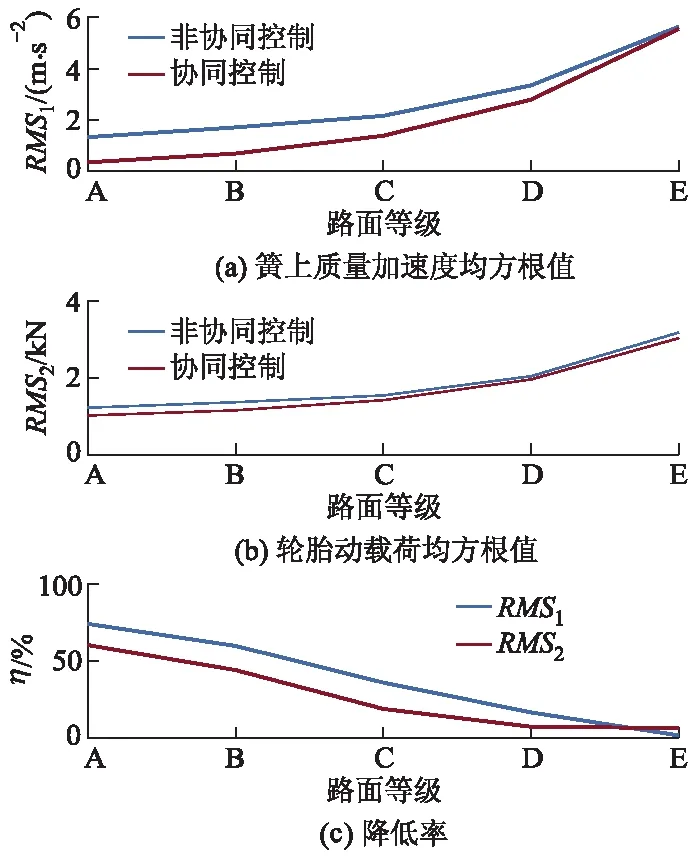
图7 车速为108 km·h-1时2种控制的性能对比

从图5-7可以看出：在3种车速和不同路面等级下，协同控制相比于非协同控制的2个评价指标均得到了明显的改善，但降低率随着路面等级的增大而逐渐减小，这是由于路面等级增加时，路面激励更加剧烈，而阻尼与车身高度控制系统所能提供的悬架力的范围不变，从而限制了悬架性能提升.

3 实车试验结果与分析

一般整车可直接测量的量有各位置的加速度、悬架动行程及簧上质量质心在车厢地板投影位置处的三轴加速度和三轴角速度，其中只需要部分可测量即可进行整车的状态变量估计.由于整车状态量的观测估计在试验中具有不可替代的作用，针对悬架控制的7自由度整车观测器设计已有较多的研究，本研究以卡尔曼观测器来获得整车的状态量[11].

基于整车观测器，以南京金龙客车制造有限公司生产的NJL6706BEV型22座中型客车为试验样车(图8)，对控制策略进行验证.

图8 试验样车

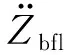
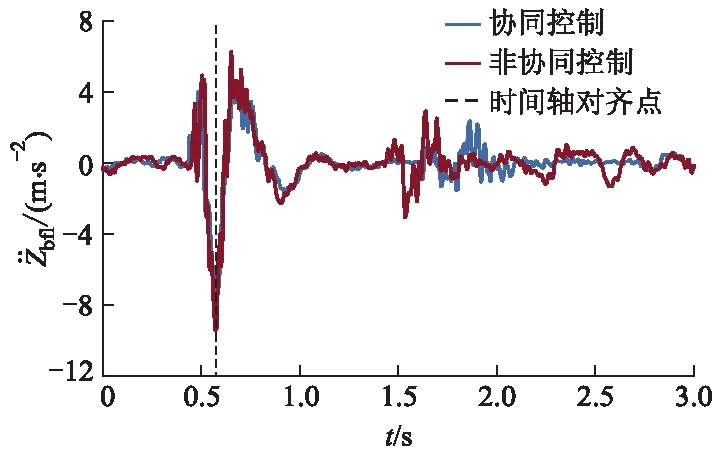
图9 前左簧上质量加速度的变化曲线

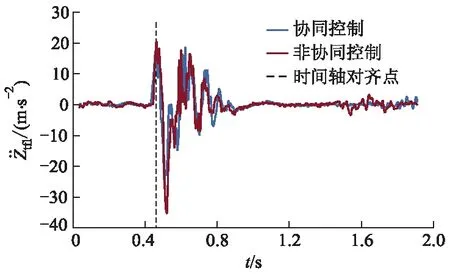
图10 前左簧下质量加速度的变化曲线

从图9可以看出：在有减速带的工况下，采用协同控制策略时，簧上质量加速度峰值范围为[-7.11，4.69] m·s-2，而采用非协同控制策略时，车辆簧上质量加速度峰值范围为[-9.44，6.26]m·s-2，相比于非协同控制策略，采用协同控制策略可在有较大路面激励时缩小25%的簧上质量加速度峰值.

从图10可以看出：在有减速带的工况下，采用协同控制策略时，簧下质量加速度峰值范围为[-26.05，18.98] m·s-2，而采用非协同控制策略时，车辆簧下质量加速度峰值范围为[-35.29，20.39]m·s-2，相比于非协同控制，采用协同控制策略后，簧下质量加速度峰值缩小了19%.

车辆在转弯工况下簧上质量侧倾角的变化曲线如图11所示，在转弯工况下，采用协同控制能较好地抑制簧上质量侧倾角；采用协同控制策略时，簧上质量侧倾角峰值范围为[-6.75°，-0.05°]；采用非协同控制策略时，簧上质量侧倾角峰值范围为[-8.04°，0.06°]；与非协同控制相比，协同控制在转弯时降低了17%的簧上质量侧倾角峰值.

4 结 论

对于空气悬架系统中可调阻尼减振器与车身高度控制系统的协同控制问题，基于模型预测控制理论，构建模型预测控制器求解当前状态下的最优悬架力，并求解阻尼器与车身高度控制系统生成该最优悬架力的具体动作，以此达到阻尼器与车身高度控制系统的协同.

协同控制仿真结果表明：在低速、中速和高速3种车速下，相比于非协同控制，采用协同控制后，整车簧上质量加速度均方根值和轮胎动载荷均方根值指标上得到了显著改善.簧上质量加速度均方根值的降低率为4%～61%，轮胎动载荷均方根值的降低率为6%～56%.而在车速20 km·h-1的有减速带和转弯工况下的实车试验结果表明：所提的协同控制策略与非协同控制相比，在路面存在较大阶跃激励时可降低25%的车辆簧上质量加速度和19%的簧下质量加速度峰值；而在转弯工况下，可降低17%的车身侧倾角峰值.仿真与实车试验2方面皆表明了所提协同控制策略的有效性.

所提的协同控制策略解决了传统协同控制中各可控结构间的性能耦合问题，避免陷入对各可控结构参数反复寻优的困境，具有一定的理论与实用价值，后期建议可考虑更多的可控结构间的协同，进一步挖掘空气悬架系统性能.