纵荡与升沉耦合激励下晃荡波特性及响应规律研究
2021-08-24刘飞飞邹寅劼刘名名李登松朱红钧
金 鑫,刘飞飞,邹寅劼,任 律,刘名名,6,李登松,朱红钧
(1.成都理工大学 能源学院,成都 610059; 2.河海大学 海岸灾害及防护教育部重点实验室,南京 210098;3.天津大学 水利工程仿真与安全国家重点实验室,天津 300072;4.淄博市公用事业服务中心,淄博 255000;5.水电水利规划设计总院,北京 100120; 6.大连理工大学 海岸和近海工程国家重点实验室,大连 116024; 7.四川农业大学 水利水电学院,雅安 625014;8.西南石油大学 油气藏地质及开发工程国家重点实验室,成都 610500)
经济的发展离不开能源的支撑,随着陆上油气资源的日益枯竭,各国均加大海洋油气资源的开采和勘察力度。船载运输具有成本低的优点,目前被广泛采用,流体晃荡问题也不可避免,同时也是海洋工程中的热点问题。在一些极端海况下,船载流体在多自由度海浪作用下极易不稳定,形成的剧烈晃荡波极有可能破坏液舱的结构甚至引起运输船的倾覆,因此亟需对流体晃荡问题深入研究。
早期研究以势流理论为基础,对单自由度纵荡、升沉、纵荡与升沉耦合激励下的流体晃荡问题进行分析(Faltinsen[1];Benjamin和Ursell[2];Hill[3];Frandsen[4]),用于预测晃荡波高及频谱特性。Faltinsen等[5]证实高阶模态对晃荡波的非线性波浪特性具有重要影响。Frandsen和Peng[6]试验地研究单独纵荡或升沉激励下的流体晃荡问题,发现充液深度对波浪的非线性响应具有重要贡献。卫志军等[7]对超大型储船内的流体晃荡进行实验研究,针对晃荡荷载进行系统的分析。Xue和Lin[8]和Xue等[9]对多种激励形式下的晃荡波进行分析并讨论内部结构对共振波的影响机制。
随着计算机硬件的发展,数值模拟逐步流行。早期的数值模型以Euler方程为基础,相关学者对二维和三维问题进行系统的研究,数值方法包括边界元法、有限差分法、光滑粒子流体动力学法、移动粒子半隐式法等(Nakayama和Washizu[10];Okamoto和Kawahara[11];Cho等[12];Gingold和Monaghan[13];Yang等[14];Wu等[15];田昀艳[16])。由于势流模型无法真实反映完整的流体运动规律,Navier-Stokes模型逐步发展起来,研究人员对强非线性和完全非线性晃荡问题进行数值模拟研究,对晃荡波高与激励频率的响应关系进行细致分析,讨论激励频率、激励振幅、充液深度对晃荡波高与荷载的影响规律(Ramaswamy[17];孙江龙和叶恒奎[18];Shao等[19];Luo等[20-21])。
Frandsen[4]推导出纵荡与升沉耦合激励下流体晃荡问题的解析解,发现耦合激励频率的线性组合满足一定条件时,波高会出现指数型增长。Ning等[22]开发了一套基于边界元算法的数值模型证实Frandsen[4]的结论。Sriram等[23]通过有限元模型分析耦合激励下的流体晃荡问题,得到流体晃荡响应的频谱特性。相关研究证实共振波有激发的趋势,但长时间的试验或数值模拟结果很少被研究,共振波的具体形式或频率组合规律的研究相对较少。本文将着重分析耦合激励下共振波及其非线性特性,同时也将对耦合共振激励的频率组合规律开展研究工作。
1 线性晃荡理论
考虑长度为L、水深为h的二维棱柱形封闭充液箱在水平x方向(纵荡)和垂直y方向(升沉)激励下的受迫运动,箱体运动轨迹分别为
X=X(t)=ahcos(ωht)
Z=Z(t)=avcos(ωvt)
(1)
式中:ah和av分别为水平与垂向的激励振幅(m),ωh和ωv分别代表水平与垂向的激励频率,rad/s。
假设流体是无粘、不可压,则流体是有势φ,其速度势φ与波高ζ可以表示为
(2)
式中:kn=(2n+1)π/L。
经过数学推导可得(具体过程参考Frandsen[4])
(3)
因此,得到纵荡与升沉耦合激励下流体晃荡的一般形式
(4)

求解上述非齐次方程,叠加不同模态下的波高,即可得到纵荡与升沉耦合激励下晃荡问题的理论波高。如果只考虑升沉激励,不考虑纵荡的影响,可得到齐次Mathieu方程,即为单独升沉激励晃荡问题。当该方程的解呈现出指数型增长,即升沉参数位于不稳定区,其他情况下流体的运动强度微弱,属于稳定区内的流体晃荡。根据Frandsen[4],第一与第二不稳定区分别位于ω1/ωn= 0.5与ω1/ωn= 1.0的附近。
2 数值模型与验证
2.1 流体运动控制方程
本文采用不可压缩流体运动控制方程为Navier-Stokes方程组,可表示为
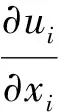
(5)
(6)
式中:i和j为自由指标(i,j= 1, 2, 3),分别代表x,y,z三个方向上的分量;ui为流体速度分量;ρ为流体密度;p为压强;gi为i方向的重力加速度分量;fi为i方向的箱体运动加速度分量。由于本文只考虑纵荡和升沉运动,因此流体运动控制方程中fi可写为
(7)
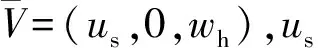
2.2 数值模型验证
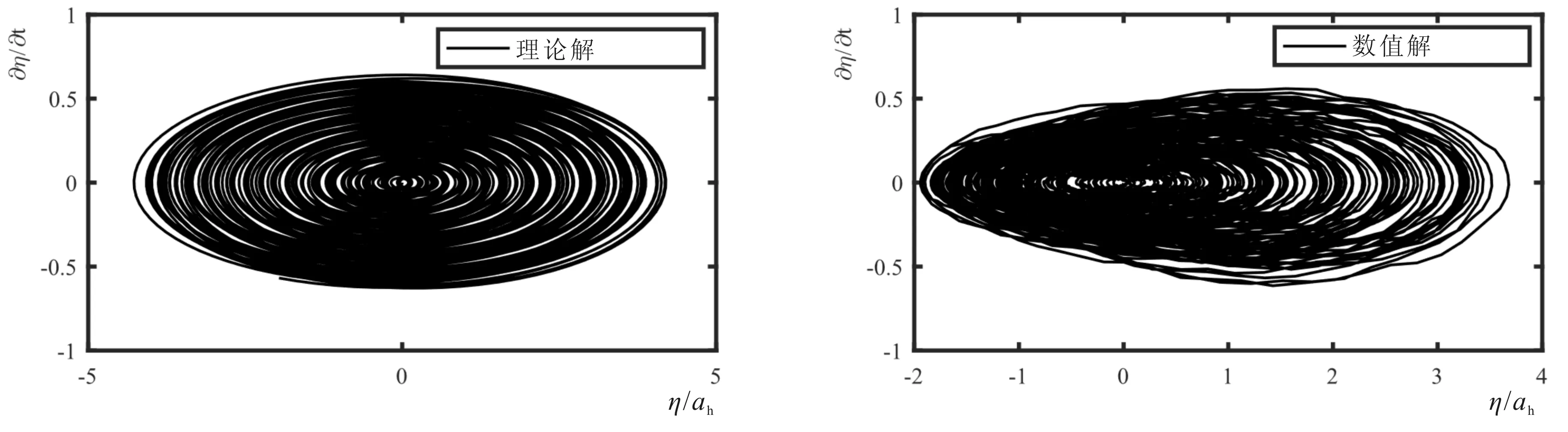
Frandsen[4]利用有限差分数值模型研究纵荡与升沉耦合激励下的晃荡问题。箱体长度L=1.0 m,水深h=0.5 m,一阶自然频率ω1=5.316 6 rad/s。纵荡与升沉均按余弦形式做周期往复运动,参数分别为:ah= 0.000 506 m,ωh= 0.98ω1,av= 0.272 4 m和ωh= 0.8ω1。二维计算域采用400×1×240的均匀网格系统,最小网格为0.002 5 m。图 1给出左边壁自由液面高程的时间历程的理论解、文献数据与本模型结果的比较关系及相应的波高相位图。从图1-a中可以发现:本模型与Frandsen的数值解[4]吻合良好,二者与理论解在无量纲时间t×ω1= 52之后偏差逐步增大,主要由于理论解忽略波浪的非线性。考虑到纵荡激励接近一阶自振频率,一阶模态共振波被激发。理论解与本模型结果的波高相位图分别如图1-b和图1-c所示,可以发现,理论解呈现出对称螺旋状的增长,而本模型考虑流体运动的非线性,表现出明显的不对称性。
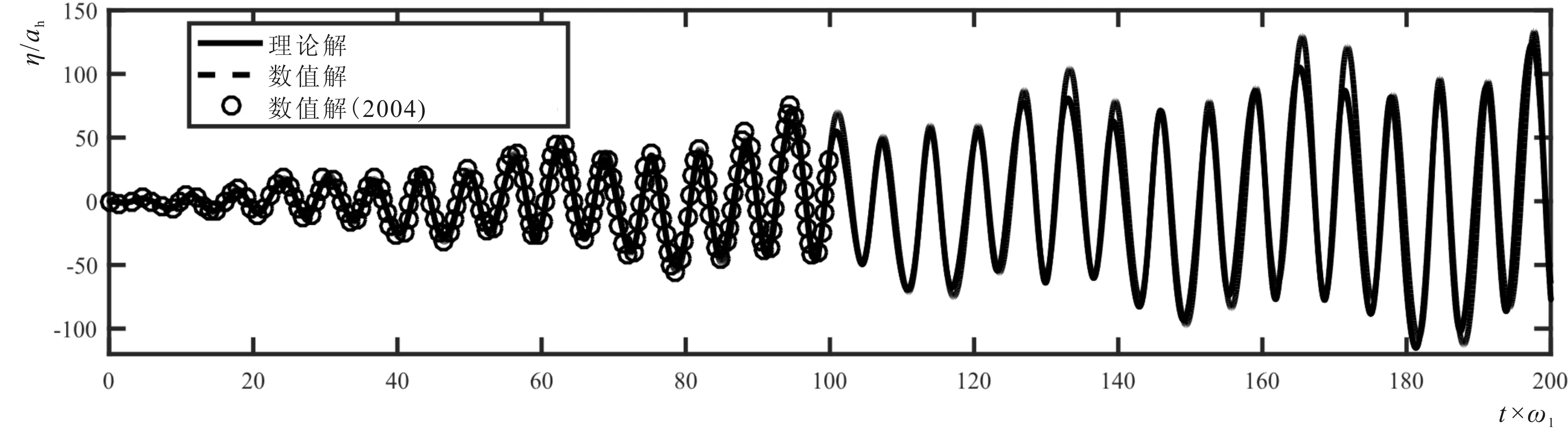
1-a 时程曲线对比

1-b 理论解轨迹1-c 数值解轨迹注:ah = 0.000 506 m,ωh = 0.98 ω1, av = 0.272 4 m,ωh = 0.8 ω1。图1 纵荡与升沉耦合激励下箱体左边壁自由面高程的时间历程曲线及相应的波高相位图Fig.1 Time series of free surface displacements at the left wall and corresponding wave-phase diagrams under coupled surge and heave excitations
3 计算结果与分析
在实际情况中,运输液舱在单独纵荡或升沉激励作用下的情况较少,一般以耦合激励为主。本文主要讨论纵荡与升沉耦合激励下的流体晃荡问题,分为三类,Case 1和Case 2:纵荡激励频率低于一阶自然频率且升沉处于稳定区;Case 3:纵荡激励频率高于一阶自然频率且升沉处于稳定区;Case 4:纵荡激励频率远离一阶自然频率,升沉参数处于第一不稳定区。相关参数总结如表1。鉴于Case 4必然会激发共振晃荡波,下面重点讨论Case 1~Case 3,在此基础上将讨论耦合激励晃荡自由面高程与激励频率间的响应关系。箱体尺寸为:长度L= 0.5 m,水深h= 0.3 m,一阶自然频率ω1= 7.672 rad/s。
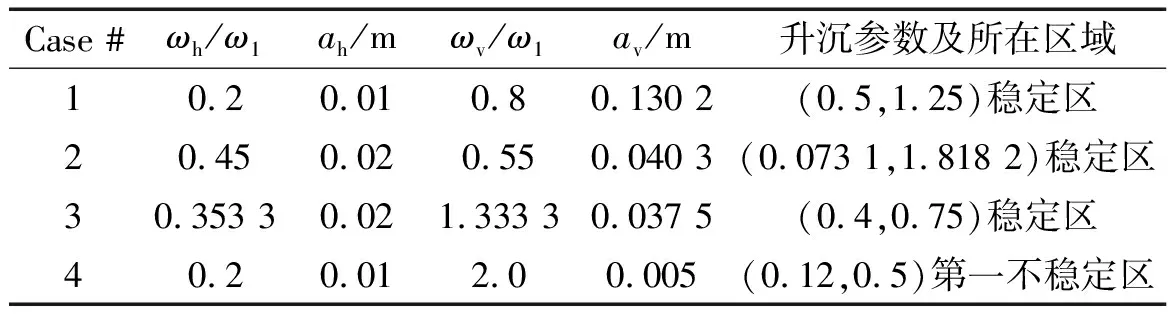
表1 纵荡与升沉耦合激励参数Tab.1 Excitation parameters for coupled surge and heave sloshing
3.1 频率和值为ω1
Case 1和Case 2的纵荡频率偏离一阶自然频率,均属于非共振激励;升沉激励参数位于稳定区,二者均无法单独激发明显的波浪运动。激励频率的和值ωh+ωv等于一阶自然频率ω1,属于共振频率。Case 1左边壁处自由面高程的时间历程曲线及相应的波高相位图如图2所示。尽管有指数增长的趋势,由于纵荡频率远低于共振频率且激励振幅较小,共振特性不明显。理论与数值结果均呈现出增长包络线,如图 2-a所示,这与单独纵荡激励晃荡较为接近;随着波高的逐步增大,数值解逐步表现出非对称性,如波高相位图如图 2-c所示。
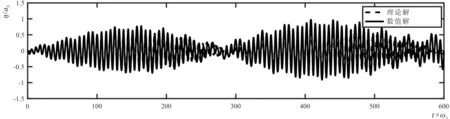
2-a 时程曲线对比

2-b 理论解轨迹2-c 数值解轨迹注:ah=0.02 m,ωh=0.2 ω1, av=0.130 2 m,ωv=0.8 ω1。图2 Case 1左边壁自由面高程的时间历程曲线及相应的波高相位图Fig.2 Time series of free surface displacements at the left wall of Case 1 and corresponding wave-phase diagrams under coupled surge and heave excitations
经过长时间模拟Case 2,得到左边壁处自由面高程的时间历程曲线及相应的波高相位图,如图 3所示。可以发现,由于非线性的影响,波高不会无限增长,且包络周期明显减小。共振特征十分明显,这与单独纵荡或稳定升沉激励下的晃荡有着显著不同。Case 2与Case 1比较而言,纵荡频率逐步靠近共振频率(一阶自然频率),且纵荡加速度逐步增大,波高增长明显,且能达到纵荡振幅的3.5倍,接近7.0 cm,非线性逐步占据主导,因此理论解与数值解在无量纲时间t×ω1= 250之后的偏差逐步增大,数值解的不对称性十分明显,如图3-c的波高相位图所示,而理论解的波高相位图(图3-b)始终呈现出对称性。不同时刻自由液面波形如图 4所示,可以发现,明显的共振晃荡波被激发,最大波高总出现在箱体壁面,波长接近箱体长度的2倍,明显的一阶共振波形。
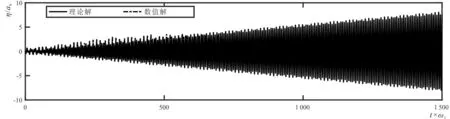
3-a 时程曲线对比
3-b 理论解轨迹3-c 数值解轨迹注:ah = 0.02 m,ωh = 0.45 ω1, av = 0.040 3 m,ωv = 0.55 ω1。图3 Case 2左边壁自由面高程的时间历程曲线及相应的波高相位图Fig.3 Time series of free surface displacements at the left wall of Case 2 and corresponding wave-phase diagrams under coupled surge and heave excitations
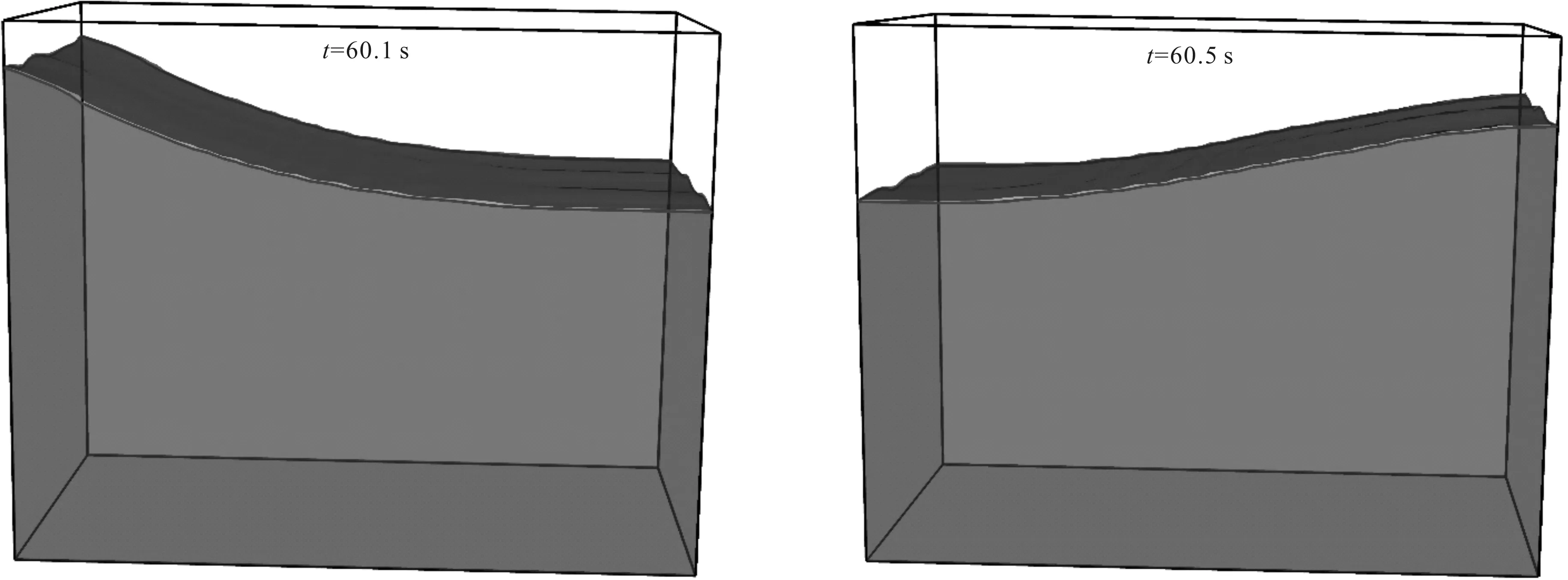
图4 Case 2自由面波形图Fig.4 Free surface snapshots of Case 2
3.2 频率差值为ω1
激励频率差值ωv-ωh等于一阶自然频率ω1的Case 3也进行了数值模拟研究,相应左边壁处自由面高程的时间历程曲线及相应的波高相位图如图 5所示。与Case 2比较,Case 3的纵荡频率较低,纵荡振幅一致,尽管升沉激励均处于稳定区,但Case 3的波高较Case 2大,表明差值组合较和值组合的工况更容易激发共振波形。同样地,由于非线性的影响,数值波高与线性解在波高较大时差异明显,呈现出非对称的形状且大于理论解,如图 5所示;非线性特性也可以从自由面高程相位图(图 5-c)发现。不同时刻自由液面波形如图6所示,可以发现,明显的一阶模态的共振晃荡波被激发,与Case 2类似,波长接近箱体长度的2倍。

5-a 时程曲线对比

5-b 理论解轨迹5-c 数值解轨迹注:ah = 0.02 m,ωh = 0.353 3 ω1, av = 0.037 5 m,ωv = 1.333 3 ω1。图5 Case 3左边壁自由面高程的时间历程曲线及相应的波高相位图Fig.5 Time series of free surface displacements at the left wall of Case 3 and corresponding wave-phase diagrams under coupled surge and heave excitations
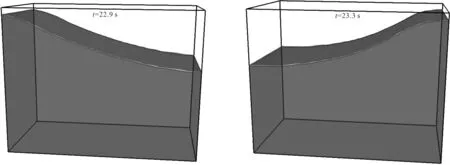
图6 Case 3自由面波形图Fig.6 Free surface snapshots of Case 3
从Case 1~Case 3的模拟结果可以发现,即使单自由度的稳定区升沉激励或纵荡非共振激励不能激发出连续增长的共振形态,当耦合激励满足一定条件时,即:它们的差值或和值等于自然频率时,也能激发共振晃荡波。
3.3 扫频响应
上述研究表明:当纵荡和升沉激励均处于非共振时,耦合激励下的晃荡在某些组合下也会出现共振特性,下面将对纵荡和升沉耦合激励下的流体晃荡响应进行系统的分析。在保证纵荡和升沉激励加速度恒定的情况下,系统地改变纵荡和升沉激励频率,考察波高η随频率的响应过程,即:扫频分析,分为两种工况:第一种,纵荡激励非共振,系统地改变升沉激励参数;第二种,升沉激励处于稳定区,系统地改变纵荡激励参数。
3.3.1 纵荡扫频响应
升沉运动在数值模型中设置为av=0.130 2 m,ωv= 0.8ω1,属于稳定区的升沉晃荡。保持升沉参数不变,系统地改变纵荡激励频率,相应的角频率为0.383 6 rad/s到17.645 6 rad/s,对应[0.05ω1, 2.3ω1]。保持纵荡加速度不变,即:ahωh2/g=0.01 g的情况下,水平激励频率从0.05ω1系统地增大2.25ω1,对应纵荡激励振幅为[0.666 7 m, 0.000 3 m]。理论解的频率间隔为0.01ω1,数值解的频率间隔为0.05ω1。图7给出自由面高程-纵荡激励频率的响应曲的理论解与数值模拟结果的对比关系。可以发现,当激励频率线性组合偏离自然频率时,理论解和数值结果较为吻合,当频率线性组合接近自然频率时,数值结果和解析解存在一定的差异,主要是由于共振诱发的非线性引起的。图7中各峰值对应频率分别为0.18ω1、0.625ω1、1.0ω1、1.45ω1、1.75ω1和2.25ω1,其中:0.18ω1和升沉频率的和值接近一阶自然频率ω1;0.625ω1和升沉频率的和值接近第二阶自然频率ω2;一阶自然频率ω1,其自由面高程最大;1.45ω1接近第二阶自然频率ω2;1.75ω1接近第三阶自然频率接近ω3;2.25ω1和升沉激励频率的差值接近第二阶自然频率ω2。结果表明:当二者频率和值或差值接近自然频率时,自由面高程明显高于低于该值的区域,单独纵荡激励接近自然频率时,也会激发共振波。

图7 稳定区升沉激励与扫频纵荡下左边壁自由面高程-纵荡激励频率相应曲线Fig.7 Free surface displacement vs. surge frequency for the sweeping surge test with stable surge frequency
3.3.2 升沉扫频响应
纵荡参数固定不变,设置为:ah= 0.005 m,ωh= 0.5ω1。保持升沉加速度不变,即:avωv2/g=0.25g,升沉频率从0.05ω1到 2.3ω1系统地改变,对应激励振幅从16.666 8 m递减到0.007 9 m。理论解的频率间隔为0.01ω1,数值解的频率间隔为0.05ω1。图8给出左边壁自由面高程-升沉激励频率的响应曲线结果,同时也标出升沉激励所在不稳定区的分布。鉴于线性理论解在不稳定区会指数型增长,无量纲自由面高程非常大,不便于结果对比,因此在图中单独列出比较完整的解析响应(图8),其中虚线覆盖区表示自由面高程迅速增长的区域。可以发现在第一不稳定区自由面高程明显大于其他工况,同时也可以看出,横坐标为0.5、1.0、1.5、1.75、2和2.25时,晃荡的波高明显大于偏离该频率的工况。对于横坐标为0.5工况,它和纵荡激励频率的和等于一阶自然频率ω1;横坐标为1.0即是一阶自然频率ω1,同时也处于第二不稳定区;横坐标为1.5时,它和纵荡激励频率的差值等于一阶自然频率ω1;横坐标为1.75时,纵荡激励频率接近第三阶自然频率ω3;横坐标为2.0时,处于第一不稳定区,对应的波高最大;横坐标为2.25时,它和升沉激励频率的差值接近第三阶自然频率ω3。
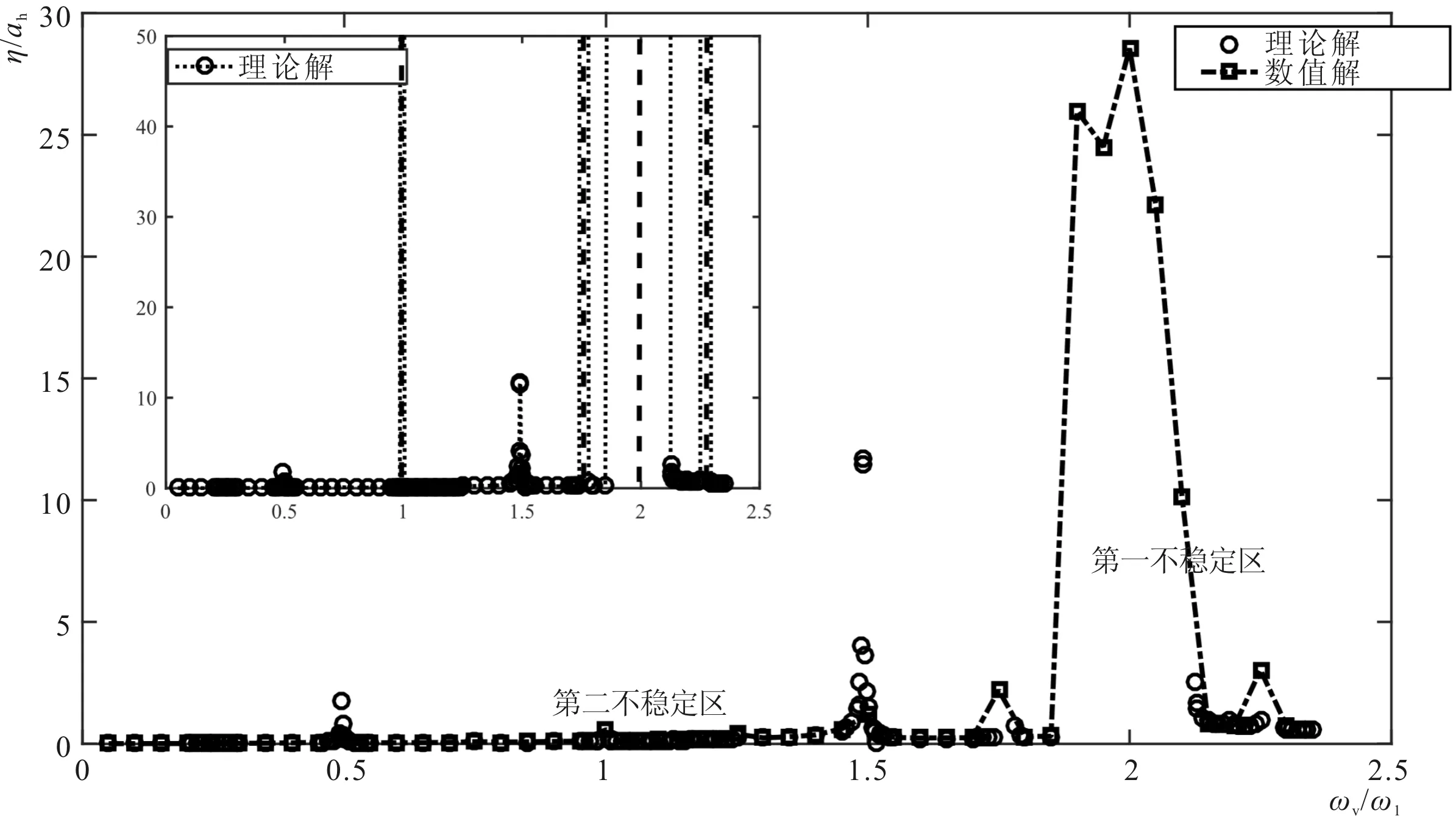
图8 非共振纵荡激励与扫频升沉下左边壁自由面高程-升沉激励频率相应曲线Fig.8 Free surface displacement vs. heave frequency for the sweeping heave test with off-resonant surge frequency
4 结论
本文通过有限差分法求解不可压缩Navier-Stokes方程,建立纵荡与升沉激励下流体晃荡的三维数值模型,数值模拟结果与理论解、文献中的数据比较分析,证明本模型在模拟耦合激励下晃荡问题的准确性。在此基础上,通过系统的数值模拟研究,得出如下结论:
(1)耦合激励频率的差值或和值接近自然频率时,共振晃荡波可以被激发。
(2)升沉处于稳定区的耦合晃荡以纵荡激励晃荡为主,当二者激励频率和值或差值接近各阶自然频率时,会诱发共振;单独纵荡激励接近自然频率时,也会激发共振晃荡波。
(3)非共振纵荡的耦合激励晃荡以升沉激励晃荡为主,尤其是升沉位于不稳定区的工况。
