双筒环隙旋转Couette流的流动特性分析
2021-08-24凌乃阳
路 昕 凌乃阳 盛 誉
(核工业理化工程研究院,天津300180)
同心的两个圆柱面之间的流动常被称为旋转Couette流动。同心圆筒环隙内的流动特性研究最早可以追溯到1880年,Margules[1]提出的同心圆筒黏度计的设想。在1888年,Couette[2]设计出了相对旋转同心圆筒装置来测量流体的黏度,并发表了有关黏度计的研究论文,这也是旋转Couette流得名的原因,后来类似的同心圆筒黏度计被称为Couette黏度计。
旋转Couette流除可以应用于流体黏度测量外,还广泛应用于电机转子、旋转的滑动轴承、数控机床的传动装置、汽车的旋转叶片等机械领域,该流动形式的研究对改善相关装置的机械、物理性能和提升机械装置寿命以及可靠性具有重要意义。
为探索双筒环隙的旋转Couette流的流动特性,分别通过理论推导和数值模拟开展了双筒环隙流场各物理量的分析,为实际的工程应用提供理论支持。
1 理论推导流动特性分析
1.1 物理模型
双筒环隙的物理模型如图1所示。模型由两个同轴旋转的圆柱面组成。其中,内、外筒的半径分别为R1和R2,m;内、外筒的旋转速度分别为V1和V2,m/s;环隙内筒壁面的压强为P1,Pa;环隙外筒壁面的压强为P2,Pa。
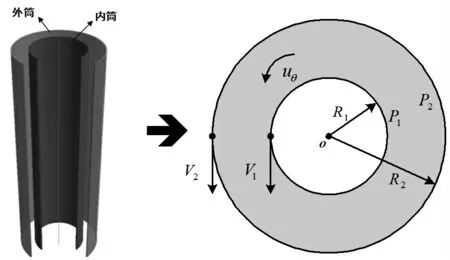
图1 物理模型
1.2 基本假设
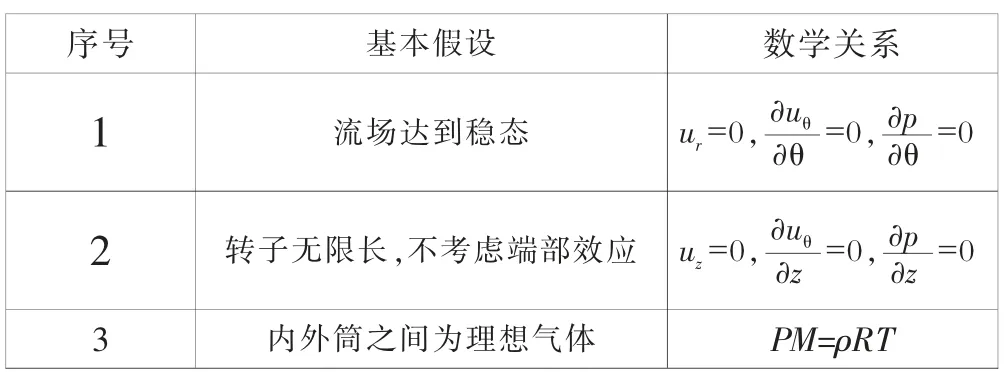
表1 基本假设
1.3 控制方程
根据以上推论得到的数学关系,得到该物理模型的控制方程

根据物理模型中的物理量,可得以下边界条件:
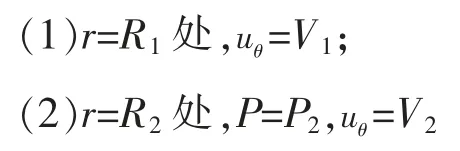
1.4 理论结果
1.4.1 角向速度分布

双筒环隙内的流动属于典型的旋转Couette流,其角向速度的径向分布呈“线性+双曲”的分布形式。
1.4.2 径向压力分布
根据方程1、方程2和方程4,可进行压强的解析推导。带入边界条件,那么压强的表达式为:
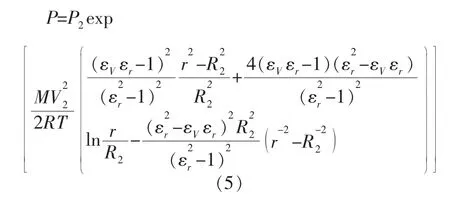
2 流动特性的数值模拟
采用CFD软件的Fluent对双筒环隙的旋转Couette流的流动特性进行数值模拟,对流场的速度和压力等参数进行对比与分析。
2.1 计算方法
采用Fluent基于密度的隐式求解器进行层流的数值模拟,采用AUSM格式对矢通量进行分裂,黏性项和对流项采用二阶中心差分格式离散。
2.2 计算模型及条件
计算模型选取双筒环隙的二维轴对称模型,内外筒的半径比εR=0.7,内外筒的线速度比εv=2.0。
边界条件设置:内、外筒壁面设置为旋转的壁面条件,上、下壁面设置为周期性边界,壁面温度为300 K均温。
2.3 计算结果
以下选取环隙中轴面分析转速及压强沿径向的分布,并与公式(4)和公式(5)的理论解进行对比,对比结果如图2和图3所示。线速度沿径向逐渐减小,压力沿径向逐渐增大。两者的数值模拟结果均与公式推导的理论值吻合,验证了线速度及压力分布公式的正确性。
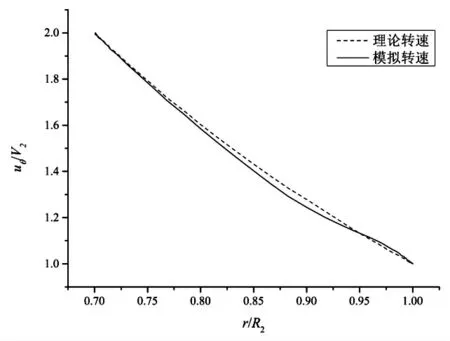
图2 转速分布对比
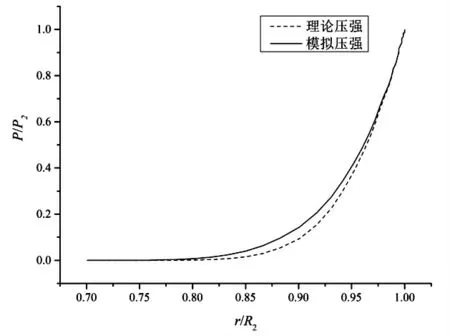
图3 压强分布对比
3 结论
本文通过理论推导和数值模拟两种手段分析了双筒环隙旋转Couette流的流动特性,得到了以下结论:
(1)双筒环隙的速度和压强等分布与内、外筒的结构尺寸和转速有关,角向速度的径向分布呈“线性+双曲”的分布形式。
(2)CFD数值仿真与理论推导的流动特性结果基本吻合。
