面向轨迹数据发布的优化抑制差分隐私保护研究
2021-08-24白雨靓李晓会陈潮阳王亚君
白雨靓,李晓会,陈潮阳,王亚君
(辽宁工业大学 电子与信息工程学院,辽宁 锦州 121001)
1 概 述
定位技术的逐步发展和智能设备的全球普及使大量移动对象的轨迹信息被持有和分享,形成了庞大的轨迹数据集,这其中所包含的信息,推动了轨迹数据分析和挖掘技术的进步,使其成为大数据安全领域的一个热点课题[1-4].研究人员通过对轨迹数据的分析和探索,从中获取大量有价值的信息用于移动对象的隐私保护研究.在数据发布过程中,不恰当的数据处理很可能会造成用户的隐私泄露,攻击者可以根据已掌握的背景知识对移动对象的个人信息进行推断,从而获得被攻击者的经济状况、家庭住址等隐私信息[5-7].但如果对轨迹数据集处理过甚,也会导致对象信息的大量损失,降低发布数据的可用性和完整性,造成信息资源的浪费[8,9].所以降低移动对象隐私泄露风险的同时提高待处理轨迹数据的可用性是一个值得深入研究的课题.
现阶段,国内外在轨迹数据隐私保护领域已取得了一些研究成果.例如,Mohammed[10]等利用一种匿名算法来实现了LKC隐私模型使其适用于RFID数据,首先识别出轨迹数据集中的最小违反序列集,然后通过贪心法对违反序列进行全局抑制,达到尽可能减少最大频繁序列损失的目的,但全局抑制的方法需要将大量数据删除,没有有效提高数据可用性.Chen[11]等人通过(K,C)L隐私模型及算法提出了局部抑制的概念.该算法首先确定轨迹数据集中不满足(K,C)L隐私模型要求的所有序列;然后在保证数据高效可用性的前提下,通过局部抑制将轨迹数据集简化.Ghasemzadeh[12]等人通过对LKC-隐私模型中C=1的情况进行研究,通过全局抑制来实现对轨迹数据的隐私保护;Komishani[13]等人提出一种泛化敏感信息的隐私保护算法,该算法通过对敏感信息属性建立分类树来实现对高维轨迹数据集的抑制,但由于不确定攻击者所掌握背景知识的长度,所以需要抑制大量数据,降低了数据挖掘价值.由此,为了提高轨迹数据发布过程中用户信息的安全性,降低由于全局抑制带来的数据损失率,本文提出了一种面向轨迹数据发布的优化抑制差分隐私保护算法.通过对大量轨迹数据集的分析结果表明,相比于其他算法,该算法在保证用户隐私信息不被泄露的同时有效降低了数据损失率,提高了数据可用性.
2 相关定义
本节主要阐述一些基本定义及相关概念,包括轨迹、违反序列、频繁序列、分类树等.
2.1 轨迹
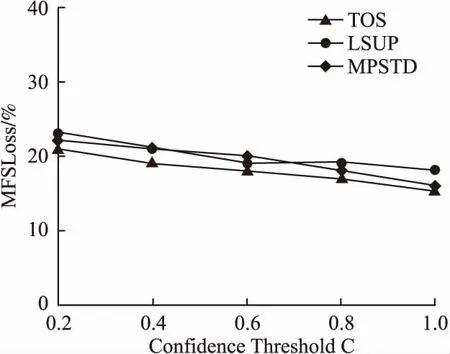
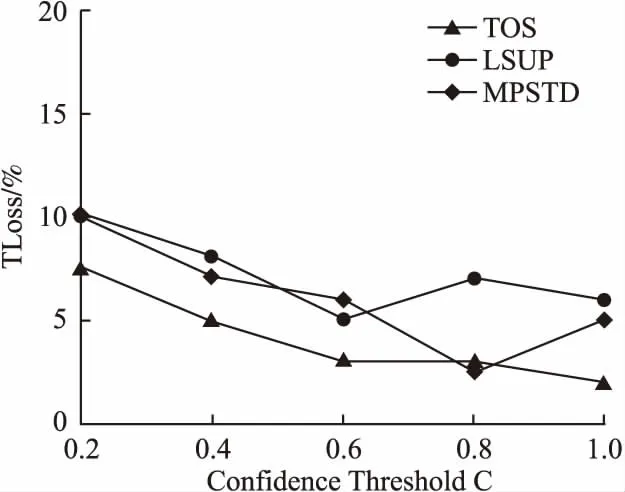
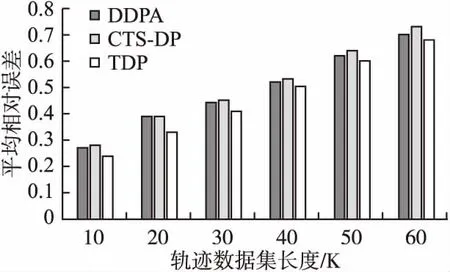
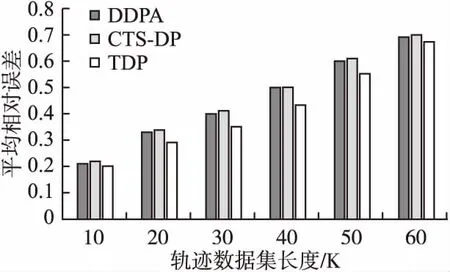
定义 1.(轨迹)[14]轨迹是空间中移动对象所产生的时间和位置的有序组合,可表示为tr=(oi;((x1,y1,t1),(x2,y2,t2),…,(xn,yn,tn))).其中:oi为用户标识符;((x1,y1,t1),(x2,y2,t2),…,(xn,yn,tn))为轨迹序列,t1 定义 2.(轨迹数据集)轨迹数据集T是一系列轨迹数据的集合,表示为:T=(tr1,tr2,…,trn),其中n表示T中包含的轨迹条数,也可用|T|表示,即|T|=n. 若轨迹数据集中的某个敏感属性和某些位置点共同频繁出现在同一序列中,攻击者不用确认移动对象的具体轨迹,也可以通过对其他拥有部分相同序列对象的分析,推断出被攻击者的敏感属性,例如表1是一个包含移动对象敏感属性的简单轨迹数据集T. 表1 轨迹数据集T 从表1可知,轨迹数据集T中,包含e2、e3两个位置点的序列有tr3、tr5、tr7这3条,其中tr3、tr5两条轨迹所对应的敏感属性均为SARS.因此,假设被攻击对象为A,当攻击者掌握A曾经到过e2、e3两个位置点这一背景知识时,其可推断出用户A患有SARS的概率为2/3=66.7%. 定义 3.(LKC-privacy)[15]L是攻击者掌握的最大轨迹长度值,T是所有用户的轨迹数据集,S是数据集T中的敏感属性值,若T满足LKC-隐私当且仅当T中任意子序列P在|P| 1)|T(p)|≥K,T(p)是轨迹中包含p的用户. 2)Conf(s|T(P)≤C,Conf(s|T(p))=|T(P∪s)|/|T(P)|,其中0≤C≤1,s∈S,C是匿名集的置信度阈值,可以根据需求灵活地调整匿名的程度. 定义 4.(违反序列)假定轨迹序列集上的序列p长度|p|满足0<|p|≤L,若序列p不满足LKC-privacy定义中的任一条件,则称p为违反序列. 定义 5.(最小违反序列)给定违反序列p,若序列p为最小违反序列(记为MVS(Minimal Violating Sequence)),当且仅当序列p的任一子序列均不为违反序列. 定义 6.(频繁序列)给定阈值E>0和轨迹数据集T中的任一子序列p,若|T(p)|≥E,则称p为频繁序列,其中|T(p)|为序列p在T中出现的次数. 定义 7.(最大频繁序列)给定频繁序列p,当且仅当p的父序列都不是频繁序列,则称序列p为最大频繁序列,记为MFS(Maximal Frequent Sequence). 定义 8.(分类树)[16]根据轨迹数据集T建立分类树,将数据集中敏感信息逐一添加到分类树的叶子节点中,叶子节点自底向上泛化成为分类树的节点,所有叶子节点的集合即为分类树的根节点,对于所有分支,划分后选择相同分支的所有实例都属于同一类.图1为根据表1数据建立的简单分类树. 图1 表1中敏感属性的简单数据分类树 差分隐私保护技术通过向数据中添加噪声技术来实现数据失真,降低数据敏感度的同时保持数据属性不变,在数据集中更改任一条数据信息,算法输出结果保持不变,所以即使攻击者掌握了除一条记录外的所有敏感数据,这一条记录中的敏感信息仍然不会被泄露. 定义 9.(差分隐私)[17]给定一个随机算法Q,Rang(Q)代表其值域,若算法Q对于任意两个邻近数据集T1和T2的输出结果O(O∈Rang(Q))均满足不等式(1),则Q满足ε-差分隐私. Pr[Q(T1)=O]≤exp(ε)·Pr[Q(T2)=O] (1) 其中,ε表示隐私预算,Pr[Q(Ti)=O]表示算法的概率,其由算法Q决定.(本文采用的差分隐私保护噪音机制为拉普拉斯噪音机制) 定义 10.(全局敏感度)输入一个轨迹数据集T,对于任一函数f:T→Rd其全局敏感度可表示为: (2) 其中,R代表映射的实数阈,d代表f:T→Rd的查询维度,‖f(T1)-f(T2)‖1表示f(T1)和f(T2)之间的1-阶范数距离. 定理 1.(拉普拉斯机制)对于任一函数f:T→Rd,给定随机算法A,则使A满足ε-差分隐私,当且仅当算法A满足等式(3). A(T)=f(T)+〈Lap1(Δf/ε),Lap2(Δf/ε),…,Lapi(Δf/ε)〉 (3) 其中,Lapi(Δf/ε)(1≤i≤d)是相互独立的拉普拉斯变量,噪音通常由拉普拉斯分布产生,噪音量大小与Δf成正比,与ε成反比. 本文提出一种面向轨迹数据发布的优化抑制差分隐私保护算法,主要包括两个部分: 1)将需要进行全局抑制的序列进行局部抑制的操作,根据位置点的抑制优先级得分决定抑制顺序,计算其可能产生的最小违反序列,并将其从轨迹数据集中舍弃; 2)建立分类树,引进差分隐私保护方法实现对轨迹数据保护操作. 面向轨迹数据发布的优化抑制差分隐私保护算法框架图如图2所示. 图2 算法框架图 第1部分(TOS):计算新产生的最小违反序列(NewMVS),具体过程如下:首先找出轨迹数据集中的MVS集合,根据给定的频繁阈值E,找出最大频繁序列集,然后构建MFS树,根据点p的抑制优先级[18]得分Score(p)来决定抑制的顺序: (4) 其中Eliminate(p)代表抑制点p可以消除的MVS数目,Loss(p)代表抑制点p带来的有用性损失.算法伪代码如下: 输入:原始轨迹数据集T、敌手掌握的轨迹长度上限L、匿名数K、置信度阈值C、敏感值合集S、最小违反序列合集MVS 输出:更新最小违反序列集(NewMVS) 1.X<-Find all MFSs from T; 2.Y<-Based an MFS tree based on the data in X; 3.For each m in MVS; 4.P<-Suppress the point p in m; 5.V<-Single violation sequence point and the violation sequence point of P; 6.Remove the points belong to V from P except p; 7.Generate a new sequence by P; 8.Loop the above operation from 3 to 7; 9.Build the score sheet by Score(p)=Eliminate(p)/Loss(p); 10.Choose the highest point; 11.If Partial inhibition; 12.Delete the highest p; 13.Update MFS; 14.Else 15.Restrain all instance; 16.Delete the MFS including p; 17.Update score sheet; 18.Return NewMVS; 第2部分(TDP):利用轨迹数据集经LKC隐私模型处理过的数据迭代构建分类树,并利用Laplace噪声机制对敏感信息进行保护[17].首先初始化数据集T,在轨迹数据集选出两组频繁序列构造一棵分类树.其思想为:挑选出每条轨迹记录中任意两个位置点出现次数最多所对应的轨迹序列作为第一组,然后在包含这个位置点的所有序列中挑出次数最小的序列,将这个序列所在的轨迹中最频繁的位置点当做第二组,以此类推,将所有轨迹都迭代挑选进分类树中,就构造好了一棵分类树T-tree(0).鉴于轨迹数据集的不断更新,所以要不断向分类树中添加新的记录,我们需要一个给定的隐私预算ε,每增加新数据集ΔTi时,ΔTi中所有记录都会被添加到T-tree(i-1)的根节点继而递归到不相交的子集中,若某些记录被添加到T-tree(i-1)的叶子节点,则需要重新分配该节点的隐私预算后才能继续分割该节点;若某些记录被添加到T-tree(i-1)的非叶子节点中,就根据T-tree(i-1)的分类方法处理这些记录;如果某些记录为空,则对下一条记录做上述步骤,直到所有节点都分配完成,形成新的分类树T-tree(i),并向分类树的叶子节点中添加拉普拉斯噪声.算法伪代码如下: 输入:轨迹数据集T,增新数据集ΔTi,隐私预算ε 输出:噪声数据集H 19.Initializes the trajectory data set T; 20.Construct matrices A based on data sets; 21.Find the sequence with the most number of occurrences of any two items in A,regard asMmax[i,j]; 22.B1=Mmax[i,j]; 23.Mmin[a,b]←the smallest set of sequences in the rows of i and j; 24.Mmax[c,d]←the largest set of sequences in the rows of a and b; 25.B2=Mmax[c,d]; 26.Repeat the above steps forB1andB2; 27.For each Δ Ti; 28.Z←all trajectory from Δ Ti; 29.Ifz→cut=the root node ofT-tree(0); 31.Put Z to the root node ofT-tree(i-1); 32.For eachzi∈ Z; 33.Ifziis leaf node; 34.Separate the node,changeε; 37.Ifziis not a leaf node; 38.Assignziaccording to the classification ofT-tree(i-1); 39.Else Ifzi=null; 40.Repeat steps 33-36; 41.ReturnT-tree(i); 42.Add Laplace to A; 43.Return H; 3.3.1 算法的第1部分(TOS) 给定原始轨迹数据集T,首先识别其中的最小违反序列集MVS,然后根据最大频繁序列集,构建MFS树,再由点p的抑制优先级得分Score(p)来决定抑制的顺序,更新最小违反序列集,时间复杂度为O(|x|L|T|),|x|为轨迹数据的维数,|T|为轨迹数据集中的轨迹条数;本算法通过更新最小违反序列对局部抑制进行优化,有效解决了全局抑制导致数据可用性降低的问题,同时通过局部抑制提高了轨迹数据安全性. 3.3.2 算法的第2部分(TDP) 本实验在Python环境下运行,由Myeclipse集成开发软件进行算法实现,实验硬件环境:处理器为Intel(R)Core(TM)i7-5500U CPU 2.40GH、RAM为8.0G、Lnuix操作系统,本文采用包含18670条真实用户轨迹的开源数据集进行实验验证[19],该数据集由微软亚洲研究院的Geolife项目提供,在轨迹数据隐私保护相关研究中广泛应用. 4.2.1 算法的第1部分(TOS) 本文中数据损失是衡量轨迹数据可用性的重要参考,本文从频繁序列(MFS)和轨迹序列两方面进行衡量[20]: 1)MFS数据损失MFSLoss,取决于原始轨迹数据集中的MFS数和经过局部抑制处理后数据集中剩余的MFS数: (5) 其中M(T)为原始轨迹数据集中的MFS数,M(T°)为经过局部抑制处理后的数据集中的MFS数. 2)轨迹序列损失TLoss,取决于原始轨迹数据集中的序列数以及经过数据处理后的序列数: (6) 其中L(T)为原始轨迹数据集中的轨迹条数,L(T°)为经过局部抑制处理后的数据集中的轨迹条数. 4.2.2 算法的第2部分(TDP) 本算法利用计数查询[17]计算数据的平均相对误差作为衡量数据损失的标准,利用计数查询R: (7) 4.3.1 算法的第1部分(TOS)结果 为了验证本文算法的有效性,将本文中的TOS算法与文献[21]以及文献[22]中的LSUP、MPSTD算法进行实验结果比对.算法中的匿名个数K、置信度阈值C均会对实验结果产生不同程度的影响,所以本实验在不同的K值(3种算法C值、L值相同)、C值(3种算法K值、L值相同)下对3种算法实验结果进行了比较: 1)不同K值对数据损失的影响 由图3、图4中的实验结果可知,当匿名数K值递增,MFS损失率和序列损失率也在随之增加,其原理在于最小违反序列集(MVS)的数目与K值成正比例关系,K值的增加导致需要被抑制的序列数增加,加大了数据损失率.相比于其他两种算法,本文中的TOS算法在数据处理过程中根据抑制优先得分优化了更新最小违反序列集的过程,合理的利用了局部抑制的优势,具有更低的MFS损失率和序列损失率. 图3 不同K值对MFS损失率的影响 图4 不同K值对序列损失率的影响 2)C值不同对数据损失的影响 由图5、图6的实验结果可知,当置信度阈值C的值递增,MFS损失率和序列损失率逐渐减小.C值的增加会减少需要抑制的最小违反序列(MVS)数,从而导致MFS损失率和序列损失率都在逐步下降.综合图3-图6数据结果,在数据处理过程中,不论是C值还是K值的递增,本文提出的TOS 算法的数据处理结果均在一定程度上优于其他两种算法,因为TOS算法是根据抑制点得分优先级来决定抑制顺序,可以更合理的更新最小违反序列集,有效降低由于抑制数据导致的数据损失. 图5 不同C值对MFS损失率的影响 图6 不同C值对序列损失率的影响 4.3.2 算法的第2部分(TDP)结果 为了验证本文算法的安全性,将文献[23]以及文献[24]中的CTS-DP、DDPA算法与本文TDP算法进行实验结果对比.实验结果表明随着轨迹数据集长度的增加,数据的平均相对误差也逐渐增加,但在隐私预算值越大的条件下,两种实验中数据的平均相对误差均在降低.从实验结果可知,相比于其他两种算法,本文中TDP算法的轨迹数据分类树是在通过局部抑制处理后的数据基础上建立的,避免了由于添加过多拉普拉斯噪声而导致的数据失真,更有效降低了平均相对误差,提高了轨迹隐私数据的可用性与安全性. 图7 ε=0.5时,数据集长度对平均相对误差的影响 图8 ε=1时,数据集长度对平均相对误差的影响 本文提出了一种面向轨迹数据发布的优化抑制差分隐私保护算法,在轨迹数据的发布过程中,通过更新最小违反序列对数据进行合理局部抑制,代替全局抑制的处理,降低了全局抑制造成的多数据损失,提高了轨迹数据的可用性,同时根据处理过后的轨迹数据集中的敏感信息建立分类树,有效减少拉普拉斯噪声添加,降低数据失真,相比于其他算法,本文提出的算法有效降低了MFS损失率和序列损失率,减小了平均相对误差,降低隐私泄露风险的同时提高了待发布数据的可用性.未来将继续对如何进一步提高待发布数据的可用性进行研究.
2.2 序列
2.3 分类树
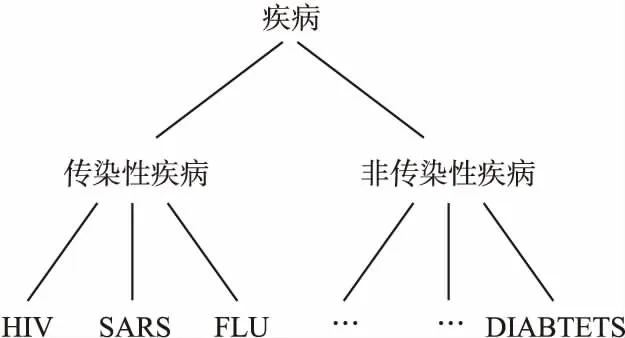
2.4 差分隐私
3 算法的基本思想
3.1 设计思路
3.2 算法描述
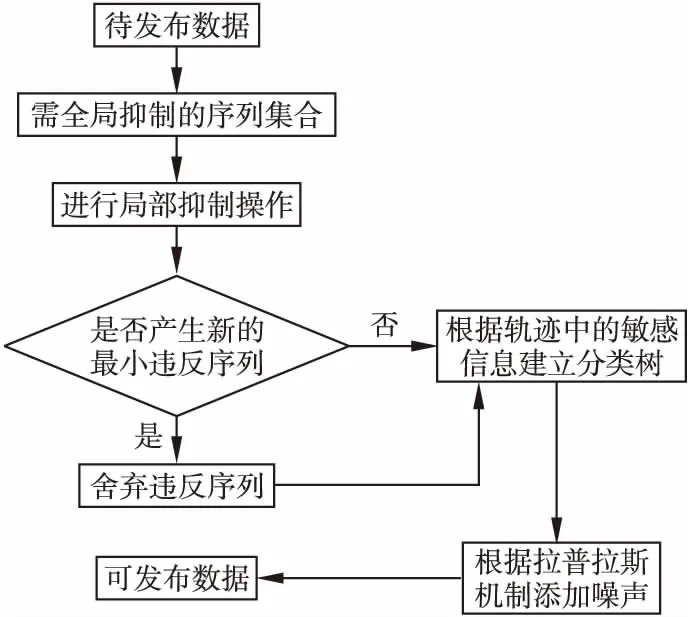
3.3 算法分析

4 实验分析
4.1 实验环境与数据集
4.2 衡量标准

4.3 实验结果
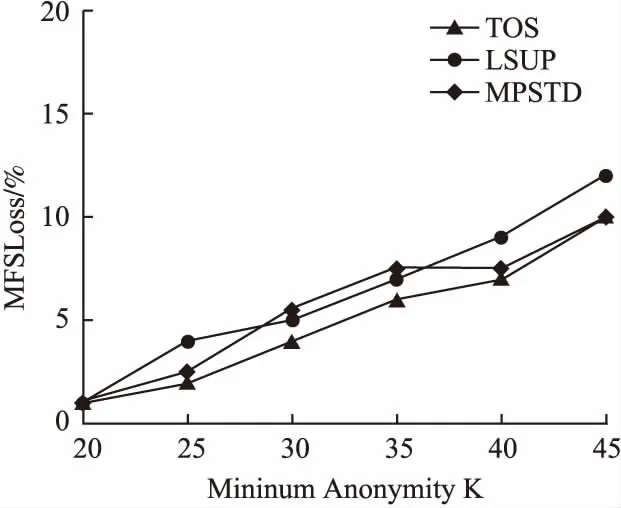
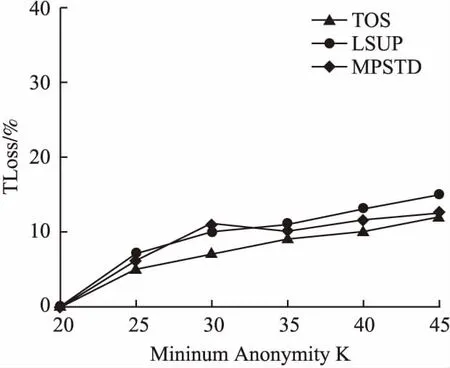
5 结束语
