兼容异构数据的稳定评估模型

曹玉红，赵 乙，陈佳桦

1(中国电子学会 科技评价中心，北京 100036) 2(清华大学 计算机科学与技术系，北京 100084) 3(北京大学 软件与微电子学院，北京 102600)

1 引 言

排序是生产和生活中用来对事物的价值或者重要程度进行评估的重要手段，并且具有显著的现实意义.比如，对于有序的集体而言，可以迅速从中选择出符合要求的个体，提高人们制定最优决策的效率.此外，排序操作在具有重要社会意义的同时，也是计算机系统中数据操作的基础.

1.1 社会意义

在社会生活中，优秀人才的推荐、项目优劣的整体评估、各类报奖评优活动的决策，都是建立在排序的基础上.合理公平的排序对于国家的优秀人才选拔、项目资金的合理分配、评奖评优的公平公正具有重要意义，是维护社会稳定、激励人们进步、促进国家未来发展的重要基石.

在大型评价活动中，为了对各个项目进行客观公正的评价，首先需要制定合理的评价指标，其次需要专业客观的评价专家和严谨的评价算法[1].在日常生活中，笔试和面试是两种常用的评价方法.笔试评价对受试者的评估流程相对固定和客观.然而，面试评价可能因为评价专家的个人经历以及专业背景的不同而掺杂专家的主观情感.特别地，为了缓解参与评价的项目众多而评价专家的人数和时间有限的矛盾，在实际生活中常常采用平行分组评价的方法.此类场景类似于研究生入学面试、毕业答辩、公务员面试等场景，并且具备本质上的相似性.对于这些场景，分组导致的组与组之间专家和项目水平的差异、以及同组内专家对评价标准的理解差异加重了面试过程中的不公平现象.

1.2 计算机系统中的意义

除了社会意义外，排序对于检索系统、推荐系统等计算机系统同样具有重要意义.概括来讲，计算机系统中的许多实际应用也可被视为一个分组评价排序问题.具体地，企业之间需要建立自己的检索系统，但是由于各个企业对数据隐私的重视使各个企业之间的数据形成了数据孤岛，在此基础上构建的基于联邦学习的排序算法[2]可以被抽象为一个分组评价排序问题.在联合检索系统中，将多个子系统检索结果列表合并成一个列表[3]，同样需要解决如何进行综合排序的问题.除此之外，计算机系统中的排序应用还有数据挖掘中对实体解析的记录对进行排序[4]，个性化推荐系统中对反馈数据进行排序[5]，程序设计中的归并排序，等等.排序作为计算机操作数据的基础，研究如何更加合理地排序对于提升用户的使用体验，进而提高应用系统的商业价值具有重要意义.

1.3 相关工作

本文以排序的社会应用为背景，重点研究如何提高分组评价排序中的公平性.比如，一些研究人员利用多目标优化方法研究了如何更加合理、更加科学地对面试中的老师和学生进行分组[6].随着深度学习等学习类算法的发展，一些研究人员利用循环神经网络和注意力机制对面试者的人格特征进行学习[7]，以准确预测面试者的总体得分.针对面试者感受到的不公平，一些研究人员提出使用机器人作为中间代理人来提高面试者的公平感知[8].

本文基于网页重要性评估的PageRank算法和HITS算法中用到的反复改进原理，设计了一种可以兼容异构数据的稳定评估模型.本文的主要工作如下：

1)建立了处理分组评价排序问题的稳定评估模型，该模型可以兼容处理分组带来的异构数据；

2)分析了分组带来的组内偏差和组间偏差，并在模型中建立相关步骤消除组内、组间偏差；

3)通过专家权重和项目得分互评，以项目得分作为中介，实现专家对专家之间的权重评价；

4)建立完整实验对模型的有效性进行了验证.

2 背景知识

本小节将介绍异构数据的基本概念以及在本文中的具体概念.同时，本小节以网页重要性评估为例，简要介绍反复改进原理以及相关算法.

2.1 异构数据

异构数据指的是一个整体数据中部分个体数据包含不同的数据特性.根据导致数据差异的原因不同，异构数据可以按照不同层次进行划分.比如，在计算机体系结构层次的异构中，数据由于存储的物理来源不同而产生异构特性.在存储的逻辑模型层次的异构中，数据分别在不同的业务逻辑中存储和维护，导致含义相同的数据在表现形式方面存在异构特性.在异型信息系统中使用不同信息描述方法及信息域划分标准，导致对同一实体的描述信息在语义表述和逻辑结构方面存在异构特性[9].这些层次的异构阻止了各个系统之间的信息交互和资源共享.

本文的异构数据，指的是不同分组之间的专家打分存在整体差异以及由于个人对评价标准理解不能达到高度一致从而导致同组专家评估时产生的差异.除此之外，本文的异构数据也包含不同分组之间项目数和专家数不同时获得的原始评分数据维度存在的微小差异.为了对异构数据进行整体利用，首先需要对数据进行转换，使数据具有相同的表现形式和含义[10].对异构数据转换的核心是指定统一标准.在本文中，统一标准指的是消除分组带来的组间偏差和专家评价标准不一致带来的组内偏差，使各个专家的评价标准尽可能统一.

2.2 反复改进原理

网页重要性评估是搜索引擎关注的基本问题.其中，PageRank算法和HITS算法是基于网页链接分析的两个重要网页排序算法，其思想都是基于反复改进原理.本文设计的模型也是利用反复改进原理，并且对PageRank算法和HITS算法中的部分理念进行了融合.

2.2.1 PageRank算法

PageRank算法是在1998年由Google创始人Lawrence Page和Sergey Brin提出来的基于链接分析的网页排序算法[11].PageRank算法利用网络的拓扑信息，能有效地识别出网络中的重要节点[12].对于网页的重要性，PageRank算法主要从两个维度来判断：某一个网页是否被多次引用，以及某一个网页是否被重要性很高的网页引用[13].在PageRank算法中，通过各个网页之间关联关系来衡量各个网页彼此之间的影响力，通过网络中出链入链的影响力，最终找出对网络具有最大影响程度的关键节点[14].PageRank算法首先会确定每个网页的PageRank值(简称为PR值)，然后根据PR值的大小对网页的重要程度进行排序.若是某个网页X中包含了指向网页Y的链接，则视为网页X对网页Y投了一票.如果有很多网页链接都指向了网页Y，则说明网页Y的重要程度较高.相应地，网页Y的PR值也就比较大.通过多次计算，反复更新网络中每个网页的PR值，最终求得每个网页的稳定PR值.

2.2.2 HITS算法

传统PageRank算法的局限性在于网页将自己的PR值平均分配给了该网页链接链出的节点，这与实际应用中网络节点交换的信息量并非平均分配这一事实不符[12].因此，康奈尔大学学者提出了HITS算法[15]来改进PageRank算法中PR值平均分配给链出节点这一局限性.HITS算法中提出了两个重要概念：“枢纽(Hub)”页面和“权威(Authority)”页面.具体地，Hub值用来衡量网页的出链，Authority值用来衡量网页的入链，两者综合起来对网页的质量进行评估.Authority页面通常会更多地被其他网页引用，而Hub页面则通过许多关键链接引用更多的Authority网页.质量高的Hub页面应该尽可能多地包含Authority页面，质量高的Authority页面则应该拥有尽可能多的与其链接的Hub页面.因此，网页的Hub值和Authority值可以相互评估.一个页面的Authority值是链接至该页面的其他页面Hub值之和；一个页面的Hub值是它链接的页面的Authority值总和[16].Authority值和Hub值利用反复改进原理，在迭代中不断更新、相互优化.

本文提出的稳定评估模型，利用反复改进原理求得专家评估项目分数的稳定权重值.

3 稳定评估模型

本小节将详细介绍本文提出的稳定评估模型，该模型可以处理实际生活和计算机系统中分组评价排序问题.该模型的处理过程可以分为偏离剔除、组间偏差调整、组内偏差调整三个步骤.为了便于描述模型的每个步骤，表1列出了文中常用的符号及其意义，每个符号的具体含义同时取决于符号的下标.

表1 符号说明

在表1中，m是一个组内专家的数量，n是该组内项目的数量.

3.1 偏离剔除

关于偏离剔除，指的是通过计算相关数据，剔除一位专家的打分.根据专家之间的打分对比和专家个人打分的离散程度，本文设计了两种偏离剔除方案.

3.1.1 方案1

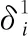
(1)

在得到每一位专家的偏离度之后，利用公式(2)来决定被剔除的专家编号.

(2)

在求出偏差最大的专家编号k之后，剔除专家k对所有项目的打分.

3.1.2 方案2

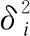
(3)

方案1有利于找到与其他专家意见相差较大的专家进行剔除，进而提高后续处理的公平性.方案2有利于找到评分范围过于离散的专家评分进行剔除，诸如存在恶意打低分或者高分.具体地，在步骤1：偏离剔除中，使用哪种偏离剔除方案可以由使用人员根据具体的使用场景自行决定.

3.2 组间偏差调整

为了消除部分评价小组评价宽松则整体成绩偏高，而部分评价小组评价严格则整体成绩偏低的现象在整体排名中引发的不公平问题，即组间差异，需要对剔除一位专家的打分后的所有分数进行归一化.归一化方法为Min-Max归一化，即公式(4).

(4)

在公式(4)中，min代表对于专家i，该专家所有打分中的最小值，max代表该专家所打分中的最大值.

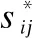
(5)

在公式(5)中，L为指定范围的下界，U为指定范围的上界.下界和上界的具体值可以根据实际的应用场景而定.

3.3 组内偏差调整

关于组内偏差调整，本文提出给每位专家分配一个权重来消除组内各个专家对考核标准的理解和评价标准的不一致而引发的不公平现象.基于PageRank算法和HITS算法中所使用的反复改进原理，本文将某一个专家的评分和其他专家的评分进行比较来验证该专家打分的合理性，进而通过调整专家的权重来提高评分的公平性.在反复改进的过程中，专家的权重改变会影响项目整体分数的变化，进而项目的排名也可能发生变化，项目整体分数变化后再重新计算专家的权重，实现专家和项目分数，专家和专家之间相互评分.

在初始阶段，本文提出的方法设置所有专家的权重为1，即wi=1 (i=1，…，m，i≠k)；而所有项目的总排名均为0，即rj=0 (j=1，…，n).随后，将某一个项目j的归一化分数与专家的权重相乘，得到项目j考虑不同专家权重的权重分数wsj(j=1，…，n)，即公式(6).

(6)

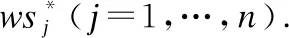
(7)

在利用公式(7)计算得到的[nw1，…，nwm]后，通过Min-Max归一化后得到更新后所有的专家权重[w1，…，wm].每次计算完项目的权重分数后，用权重分数重新对所有项目进行排名.当排名不变的次数达到指定次数时，停止更新专家的权重，得到的最新权重即为每位专家的最终权重值.在本文中，当排名次数连续10次保持不变时，计算出的专家权重值为稳定专家权重值.

计算专家权重值的步骤可以描述为算法1.

算法1.专家权重值计算算法

输入：各位专家对项目的原始分数矩阵：group_value

项目的初始排名：previous_rank

专家的初始权重：W0=[w1，…，wm]

排名保持不变的次数：keep_times

输出：每位专家稳定的权重值：W=[w1，…，wm]

1.公式(6)计算项目的权重分数

2.用权重分数计算项目的新排名new_rank

3.if(new_rank等于previous_rank)

4. keep_times加1

5.else

6. keep_times置为0

7.if(keep_times等于停止次数)

8. return [w1，…，wm]

9.else

10. 公式(7)更新[w1，…，wm]，返回步骤1

通过算法1可以得到每位专家的稳定权重值，将进行组间归一化后的分数与各位专家的权重相乘，可以得到项目的最终得分，从而可以消除组间、组内偏差，进而实现所有项目的整体排名.

3.4 模型整体描述

基于反复改进原理的专家权重与项目分数互评的稳定评估模型的整体流程描述为算法2.

算法2.模型整体流程描述

输入：专家对所有项目的打分

输出：所有项目排名

1.用公式(1)/(3)结合公式(2)计算每组偏离度最大的专家编号k

2.每组剔除编号为k的专家打分

3.使用公式(4)对每个打分进行归一化

4.用公式(5)将归一化的打分映射到[L，U]的范围

5.执行算法1得到每组专家的权重值

6.将步骤5的各个专家权重乘步骤4的分数

7.对步骤6中所有项目分数进行排序

4 实验与结果分析

本文用两组评价数据对提出的模型进行了测试.一共30个项目，分为两组：第1组17个项目，编号为1-17；第2组13个，编号为18-30.每组均有9位评审专家.为了后续叙述方便，本文将简单地使用平均值计算项目最终得分的方法记为AVE(Average)方法，而将本文提出的稳定评估模型记为SEM(Stable Evaluation Model)方法.

4.1 组间偏差调整验证

在平行分组评估中，不同组的专家对项目的评价标准和对评价标准的理解可能存在较大差异.而且，在实际生活中，由于同一个组的专家可以商量和讨论，同一组专家的评价标准将会趋向于一致，不同组专家的评价标准则更大概率存在较大差异.为了验证本文提出的稳定评估模型(SEM)能够减小组间的偏差，图1和图2展示了验证结果.

图1 基于AVE方法的两组得分

在图1中，圆圈对应的纵坐标代表1组项目利用AVE方法计算的最终得分，三角形对应的横坐标代表2组项目利用AVE方法计算的最终得分.灰色虚线是斜率为-1的参照线.将1组和2组对应名次的项目用黑色实线连接后，两组的评价标准越是一致，那么黑色实线的斜率应该越接近于-1.1组项目的AVE分数整体分布在[60，90]之间，2组项目的AVE分数分布在[60，80]之间.通过观察图1可以发现，利用平均值方法计算的最终得分中，1组项目明显高于2组项目，这说明两组专家打分的整体标准不一致，2组专家的评价标准要更加严格.

同理，可以作出利用本文提出的SEM方法得到的1组项目和2组项目的得分图，如图2所示.图2中每个元素代表的含义与图1中的含义相同.通过观察图2可以发现，本文提出的SEM方法得到的1组项目和2组项目的得分整体都分布在[70，100]之间.两组SEM分数对应名次的连线的斜率值更接近于-1，这说明SEM方法能够促进两组项目的评分标准更加一致.

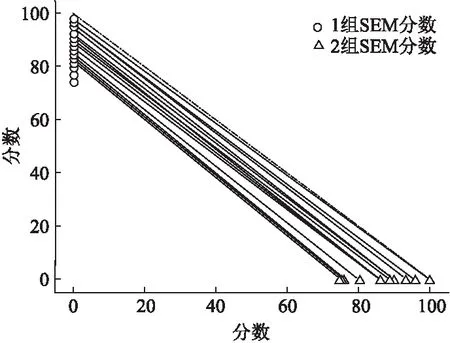
图2 基于SEM方法的两组得分

通过图1和图2对比，可以证实本文提出的SEM方法能够有效地消除不同小组评价标准不同带来的组间偏差.

4.2 组内偏差调整验证

在平行分组评价中，除了组间偏差，还有组内偏差.组内偏差是同一小组内的专家由于专业背景和对评价标准理解不一致所导致.

为了验证本文提出的模型能够有效地消除组内偏差，图3展示了专家评分分布.在图3中，横坐标代表剔除了1位专家后剩下8位专家依次排列的编号，纵坐标代表分数.虚线代表采用AVE方法时每位专家打分的范围，而三角形代表采用AVE方法时每位专家打分的平均值.实线代表采用SEM方法时，每位专家打分的范围，而五边形代表采用SEM方法时每位专家打分的平均值.通过观察图3可以发现，相比于原来的专家打分范围分布差异大，利用本文提出的SEM方法处理项目得分后，各位专家打分的范围分布一致且均匀.通过观察平均值分布可以发现，在打分平均值方面，相比于AVE方法而言，SEM方法所得到的结果整体差异较小，进而证实本文提出的SEM方法能够有效地消除组内各个专家评价标准不一致的问题.

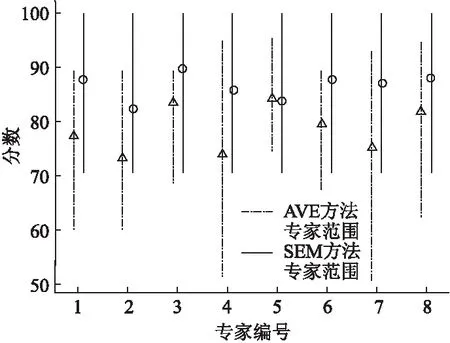
图3 专家评分分布

4.3 剔除一位专家有效性验证

为了验证SEM方法剔除一位专家的操作的必要性，本文作出了剔除一位专家和不剔除一位专家两组项目的整体排序，如图4所示.

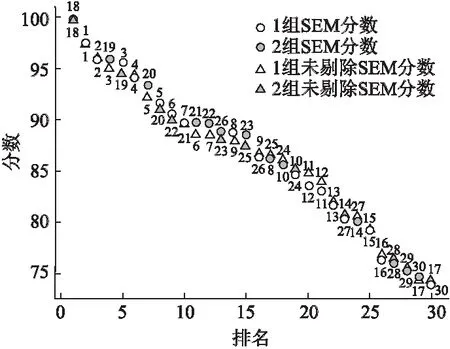
图4 剔除与不剔除一位专家分数散点图

在图4中，横坐标代表排名，纵坐标代表分数，三角形代表未剔除一位专家计算出各个项目分数的排名，圆形代表完整地利用SEM方法计算出各个项目分数的排名.空心图形代表第1组项目，实心图形代表第2组项目.图形旁边的数据代表项目的编号.图形上方的文本代表剔除一位专家得到的项目排名对应的编号，即空心和实心圆形对应的项目编号.图形下方的文本代表未剔除一位专家得到的项目排名对应的编号，即空心和实心三角形对应的项目编号.

通过观察图4可以发现，虽然剔除一位专家与否不会对所有项目的分数分布产生明显影响，但是却会影响一些项目的排名情况.本文将剔除与不剔除一位专家评分对项目排名的影响分为3种情况.情况1：对于所有专家都认可的优秀项目，如18、1、2号项目，剔除与不剔除不会影响项目的排名.情况2：对于个别专家对质量存在微小争议的项目，如19、3号项目，剔除与不剔除会影响项目前后的排名顺序.前两种情况都不能体现出剔除一位专家的必要性.但是对于第3种情况，如因为专家的专业背景与项目知识不同导致的差异、有专家恶意打低分、因私人关系打高分等情况，剔除一位专家能有效避免这些情况所引发的不公平现象，如6号项目.这与现实生活中大型体育赛事评分中需要去掉一个最高分、去掉一个最低分的目的一致.因此，剔除一位专家的打分具有合理性.而且，剔除一位专家有利于排除因专家个人偏好不同和恶意打分行为所引发的不公平现象.

5 总 结

针对平行分组评价中由于专家对打分标准的理解和评价标准不同产生的异构数据，本文提出了一种基于反复改进原理的稳定评估模型.首先，对打分专家的偏差进行计算，从而剔除一位专家的打分.然后，利用Min-Max归一化，消除组间差异.通过反复改进原理，计算出同一组内专家稳定的权重值，以消除组内各位专家的差异.通过不同维度的充分实验，实验结果验证了本文提出的稳定评估模型的有效性，并且证实了本文提出的稳定评估模型有利于消除平行分组评价中的不公平现象.