静电场电荷面密度与曲率关系的Matlab模拟研究

陈曙英，陈 钢，崔宏基

(浙江工业大学应用物理系，浙江 杭州 310023)

1 引言

对于避雷针并不陌生，它主要是利用尖端放电的原理引导雷电放电，再通过接地引线和装置将雷电引入大地，从而达到保护建筑的目的。通过对尖端放电现象的研究，人们发现随着导体表面曲率的增大，该位置的电荷密度也随之升高。在强电场的作用下，导体中比较尖锐的部分则会发生放电现象，这就是尖端放电。

尖端放电原理的应用有很多，如工业烟囱的除尘装置、电子打火装置等[1]。虽然尖端放电现象的应用很广泛，但是大多数电磁类教科书中却很少具体的讨论表面电荷密度与导体曲率之间的关系。通过相关的数值模拟，分析并得到电荷面密度与曲率的关系，可以更好的丰富这些方面的研究。

2 理论分析

在讲电荷面密度与曲率的关系前，必须先了解主曲率和平均曲率的概念。在已知曲面上取一点E，并且曲面在E点的法线为z轴，通过z轴可以得到许多剖切平面，如图1所示，向上为z轴。曲面和每个剖切平面都相交，他们的交线是一条平面曲线，每条平面曲线在E点都有一个曲率半径。不一样的平面曲线在E点的曲率半径一般是不相等的。这些曲率半径中，找出最小和最大的曲率半径，把这两个称之为主曲率半径，分别用R1和R2表示[2]。

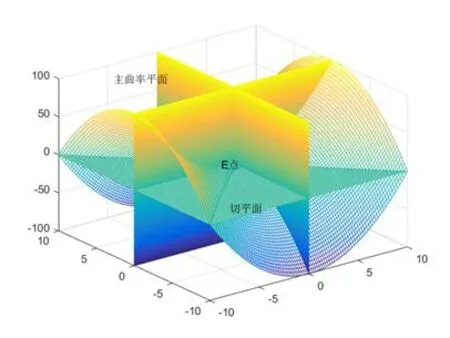
图1 曲率示意图

在众多的曲面论的问题中，起决定性作用一般都不是主曲率本身，而是由它们的平均值和乘积来决定的，即平均曲率和高斯曲率。对于一些简单的曲面，可以直接通过定义求出平均曲率和高斯曲率[3]。如式（1）所示：

H就称为曲面在给定点E 的平均曲率，K就是E 点的总曲率或高斯曲率。

本文主要是利用MATLAB 模拟计算出相关曲面的曲率和其表面的电荷面密度，然后利用数值计算找出曲率与电荷面密度之间的关系。对于曲面，可以选择椭球面、抛物面和双曲面。并且经过相关的公式推导，可以得到三个曲面的曲率和电荷面密度的严格数学关系，其中式（2）为椭球面，式（3）为抛物面，式（4）为双曲面。式（2）中K 为总曲率，Q 为椭球导体的总电荷，a和b代表赤道半径，c为极半径；式（3）中σ0为抛物面顶点（，0，0）处电荷面密度，k为常数；式（4）中a为实长轴，b为实短轴，σ0为双曲面顶点（，0，0）上的电荷面密度，k为常数。

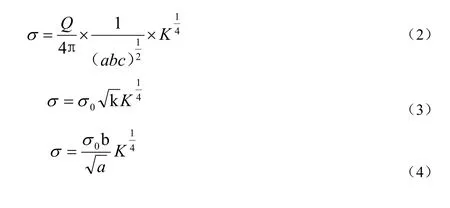
3 计算结果

计算中选择的导体的曲面为椭球面、抛物面和双曲面，并且给定整个导体所带电荷数，然后利用MATLAB中的pdetool 工具模拟出电场的空间分布图。其中椭球导体的电场分布如图2 所示。为了得到电荷面密度与曲率的关系，必须取得导体表面的电荷面密度，但pdetool 工具并不能直接给出电荷面密度的值。由于真空中静电场中导体表面附近的场强满足：

而导体表面附近任一点的E 值已经通过数值模拟计算得到，因此可以直接换算出该点的电荷面密度的值，即，可以在导体表面附近的空间取得若干个点，然后依次得到各个点的电荷面密度。

对于椭球面导体，由于椭圆的长短轴具有特殊性，因此选择点1（0，0.3）和点2（0.5，0）两个点。从图2 中得到E1=5.31，E2=6.75。再根据σ=Eε0，可以得出两点的电荷面密度σ1和σ2。同时，利用数学工具，可以得到两点的K值，分别为K1=1.20，K2=5.56。根据公式（5），E与σ成正比，所以，而。

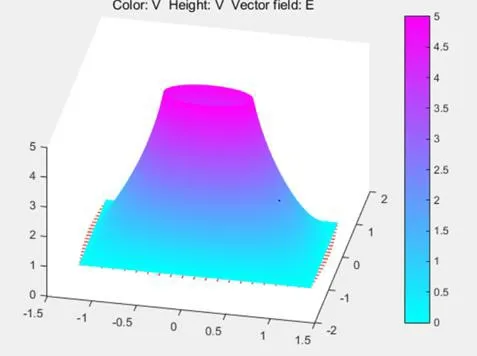
图2 椭球面导体电场分布图

对于椭球面电荷密度与曲率四分之一次方成正比[5]，而数值模拟给出的比值约为0.68，虽然比值之间存在误差，但还是在误差范围之内。对于造成误差的原因主要有以下几种：首先是数值模拟的椭圆不是真正意义上的椭圆，具有棱角；其次有限元计算时空间要进行是三角分割，对计算有一定影响。

对于抛物线，在取点之前需要先确定定义域，然后任取两个坐标点。分别以两个坐标点为中心，得出附近点的具体坐标值和对应的电压值。通过数据的筛选，选择抛物线的顶点坐标（0，0），并且随机取得坐标（0.3，0.09），得出两个点曲率之比为，数值计算得到的两点的电荷面曲率之比为，数值计算和理论分析符合的非常好。

对于双曲线，选择的模型为（y+1)2-x=1，定义域为[-1，1]，得到双曲线模拟坐标三角形分割图，如图2。对于坐标点的选择，选择双曲线下半部分的顶点（0，0）和上半部分的一点（0.30，0.04）。经过计算，得出两点电荷面密度之比为，理论分析给出的曲率的四分之一次方之比为。通过不同坐标点的电荷面密度和曲率的比值，发现公式（5）仍然得到满足。通过椭圆模型、双曲线模型和抛物线模型的建立，证明了在误差允许的范围内，椭圆、抛物线和双曲线表面的电荷密度均与该处曲率的四分之一成正比。

图3

之前的实验中，都是选取若干个点进行比较，虽然最后得出了电荷面密度与曲率的关系，但说服力不足，因此选取整条边来进行证明。通过数据的处理，得出抛物线、双曲线和椭圆的一整条边上的E值和曲率。通过Matlab 中的Cftool 工具，拟合出E值与曲率的关系图如下：

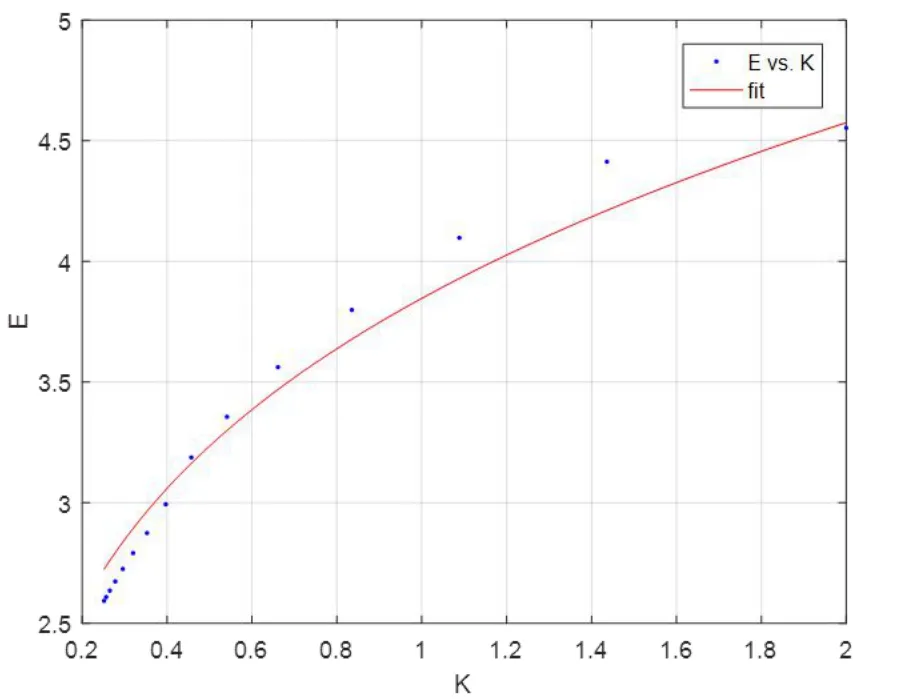
图4 椭圆拟合曲线

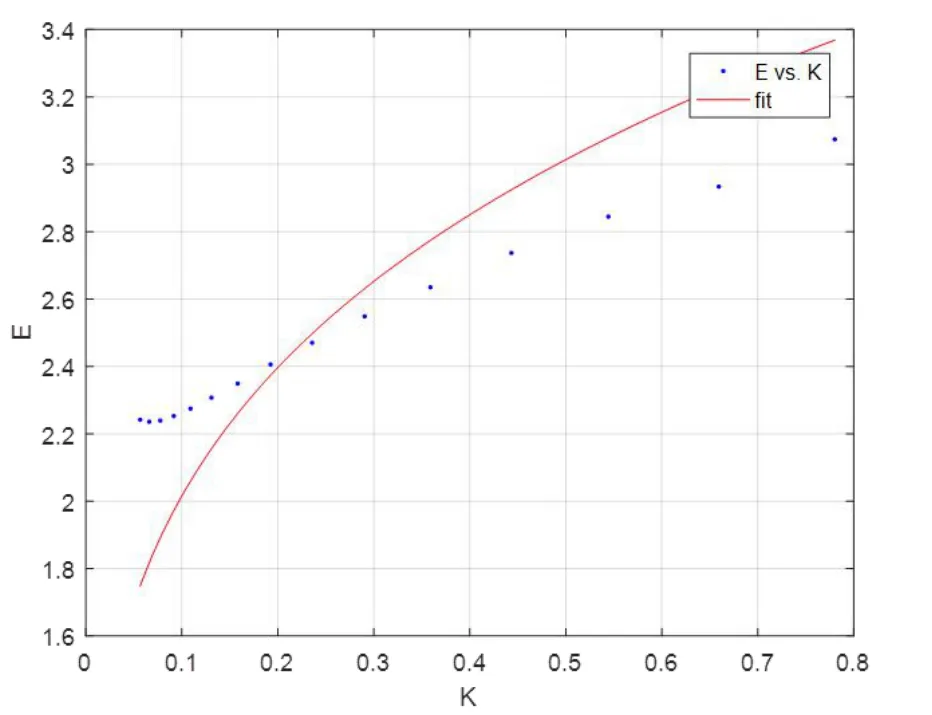
图5 双曲线拟合曲线

图6 抛物线拟合曲线

通过拟合，得出拟合函数为E=a×Kb。其中，关于a和b 的取值，椭圆为a=3.847（3.772，3.923），b=0.25；双曲线为a=3.584（3.373，3.795），b=0.25；抛物线为a=3.754（3.659，3.85），b=0.25。通过拟合曲线可以看出，E和K关系基本满足E与K的四分之一次方成正比，所以可以推导出二次曲面导体表面电荷密度与曲率的四分之一次方成正比这一结论。

4 结论

利用软件模拟出静电感应过程，并从中得出一系列坐标点以及该点的电压值。经过数据的处理和计算，可以得到对应点的电荷面密度及其表面的对应曲率。将任意两点之间的数据进行对比，可以得出电荷面密度与曲率的对应关系。通过本实验的结果，证明了通过软件的模拟是可以更加方便的证明，对于二次曲面，电荷面密度与曲率的四分之一次方成正比。