基于传染病模型的群体活动中恐慌心理蔓延研究*

王瑞祥,张英华 ,秦挺鑫,王晶晶,丁时伟,高玉坤

(1.北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京 100083；2.北京科技大学 矿山避险技术研究中心，北京 100083；3.中国标准化研究院,北京 100191；4.北京城市系统工程研究中心，北京 100035)

0 引言

近年来，各种体育赛事、演唱会等大型聚众活动频繁,人员及环境复杂程度增大，大规模人群管理比较困难。一旦发生火灾等突发事件，容易引发恐慌，造成人群混乱，严重将导致踩踏事故发生。目前，国内外学者对恐慌心理蔓延规律进行研究[1-8]:Kermack等[9]提出SIR传染病模型(Susceptible Infected Recovery,SIR);Zhao[10]采用原始传染病传播模型SIS(Susceptible Infected Susceptible)分析人群情绪感染与传播现象；Hill等[11]基于传统传染病模型提出SISa模型，通过分析发现人群情绪传播与感染规律亦可通过传染病模型进行分析；Liu等[12]提出SOSa-SPSa模型(即SOS与SPS间转换)，通过将情绪分为积极情绪与消极情绪发现，消极情绪更易感染与传播；陈卫明等[13]将人群接触关系因素加入情绪感染模型，对SOSa-SPSa模型进行改进得出，人群在突发事件下自发感染与恢复过程作用大于接触感染过程。

情绪传播规律可通过传染病模型进行研究，验证突发事件中利用传染病机制与模型研究人群情绪感染的可行性。人群恐慌是引发拥挤踩踏事故重要因素，恐慌情绪使人们做出非理性决策，降低自身及整体疏散效率[14]。目前，利用传染病模型与机制对突发事件人群恐慌蔓延规律的研究较少，因此，本文基于群体活动中突发事件，利用传染病模型对恐慌心理蔓延规律以及对突发事件影响展开研究，研究结果可为相关防控措施制定提供理论基础。

1 恐慌心理对密集人群影响

恐慌心理对密集人群影响包括2个方面：

1)恐慌对密集人群心理影响。密集人群心理状态较平常会发生明显变化，恐慌心理蔓延触发密集人群心理特征，同时，人群自我保护与逃避危险意识增强，将产生极端行为心理[15]。紧急情况下，个体间因自身安全受到威胁产生激烈竞争，甚至做出损人利己行为，形势越紧迫，竞争越激烈。

2)恐慌对密集人群行为影响。当人群处于恐慌状态时，行为特点主要表现在7个方面：①明显人群波动现象。②盲目从众现象：从众行为导致人员过度聚集或疏散效率降低[16]。③人群拥挤、推搡现象：人群间相互作用力加剧，甚至能推翻砖墙、弯曲钢筋。④出于求生本能，个体运动速度明显加快。⑤出现“快即是慢”现象[17]。⑥瓶颈处拥挤成拱：拥挤人群数量不断增加，导致拱形结构崩溃，使人员跌倒并引发踩踏事故。⑦跌倒的人员成为人群疏散障碍，降低疏散效率，引发连锁反应和踩踏事故。

2 NPCN恐慌心理蔓延模型建立与改进

2.1 基础NPCN模型建立

本文基于传染病传播模型构建NPCN恐慌心理蔓延模型，如图1(a)所示。NPCN恐慌心理蔓延模型将人群分为3类：N(Normal)正常人群、P(Panic)恐慌人群、C(Cool)冷静人群。正常活动下所有人均处于正常状态，一旦发生突发事件，距离事发地点最近或最先发现事件发生人群，受惊吓首先进入恐慌状态，随恐慌信息传播，恐慌人群数量不断增加；随时间推移，事态逐渐得到控制，恐慌人群恐慌情绪逐渐减弱，并逐渐向冷静人群转化。但冷静人群的冷静状态是暂时性的，受周围恐慌人群影响，冷静人群可能再次变为正常人群，进一步向恐慌人群转化。

图1 恐慌心理蔓延模型

分别用N(t)、P(t)、C(t)表示t时刻密集人群中正常人群、恐慌人群和冷静人群比例，N(t)+P(t)+C(t)=1，总人数为Ntotal。NPCN模型如式(1)所示：

(1)

式中：α表示正常人群向恐慌人群转化概率；β表示恐慌人群向冷静人群转化概率；γ表示冷静人群受周围环境影响再次变为正常人群概率。α、β、γ取值范围均为[0,1]。

2.2 基础NPCN模型改进

突发事件发生后，恐慌心理蔓延将衍生其他事故，加剧事故严重程度。实际情况中，突发事件发生后现场应急治安人员采取相应干预措施稳定秩序，抑制人群恐慌心理蔓延。因此，本文基于基础NPCN模型，增加阻碍因子ω和促进因子ψ2种干预因子，优化模型使结果更符合实际情况。改进后模型微分方程如式(2)所示：

(2)

式中：阻碍因子ω(ω<α，ω<γ，0≤ω≤1)表示降低正常人群向恐慌人群及冷静人群向正常人群转化的概率；促进因子ψ(0≤ψ≤1)表示增加恐慌人群向冷静人群以及正常人群向冷静人群转化的概率。加入干预因子后，NPCN恐慌心理蔓延模型如图1(b)所示。

3 模型实验结果与对比分析

针对基础NPCN模型和改进NPCN模型，利用MATLABODE45函数分别求解，通过改变不同参数进行数值模拟，分析比对2种模型模拟结果。

3.1 基础NPCN模型模拟结果

α、β、γ分别取0.85、0.2、0.4，密集人群中正常人群、恐慌人群和冷静人群比例初始值分别设为N0=0.95，P0=0.05，C0=0，N、P、C动态变化如图2所示。

图2 N、P、C动态变化

由图2可知，突发事件发生后，恐慌人群比例P由初始值5%迅速上升至最大值54.06%，然后平缓下降并最终趋于稳定值50.98%；正常人群比例N由初始值95%迅速下降并最终趋于稳定值23.53%；冷静人群比例C由初始值0逐渐上升并最终趋于稳定值25.49%。为研究模型中各参数对恐慌蔓延影响，采用控制变量法分别改变恐慌率α、冷静率β、冷静损失率γ，且满足条件α>β，模拟不同参数下P的动态变化，如图3所示。

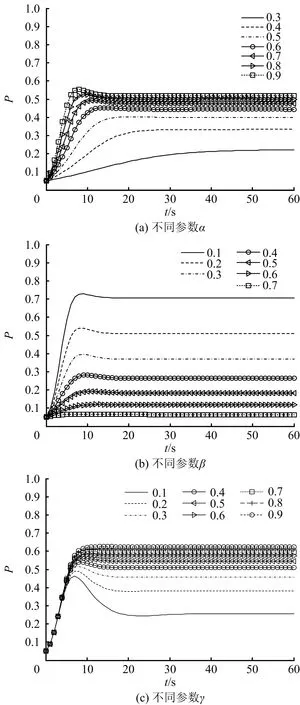
图3 不同参数下P的动态变化

1)由图3(a)可知，恐慌率α越大，系统稳定后恐慌人群比例P越大，人群恐慌程度越激烈；同时，随恐慌率α增大，P随t增速逐渐增大，P达到稳定用时越短；此外，P随恐慌率α增大不断增加，但增速逐渐减小。

2)由图3(b)可知，冷静率β越大，系统稳定后恐慌人群比例P越小，人群恐慌程度趋于缓和；同时，随冷静率β增大，P随t增速逐渐减小；随冷静率β增大，P不断降低，但降幅逐渐减小。

3)由图3(c)可知，无论冷静损失率γ取何值，系统稳定后恐慌人群比例P均迅速增加至峰值，然后下降并最终趋于稳定；γ越大，P越大，人群恐慌程度越激烈；同时，随γ增大，P达到稳定值用时越短。随冷静损失率γ增大，P不断增加，但增速逐渐减小。

3.2 改进NPCN模型模拟结果

改进NPCN模型各参数与基础NPCN模型相同，α=0.85，β=0.2，γ=0.4，阻碍因子ω和促进因子ψ均设为0.1，模拟N、P、C动态变化如图4所示。

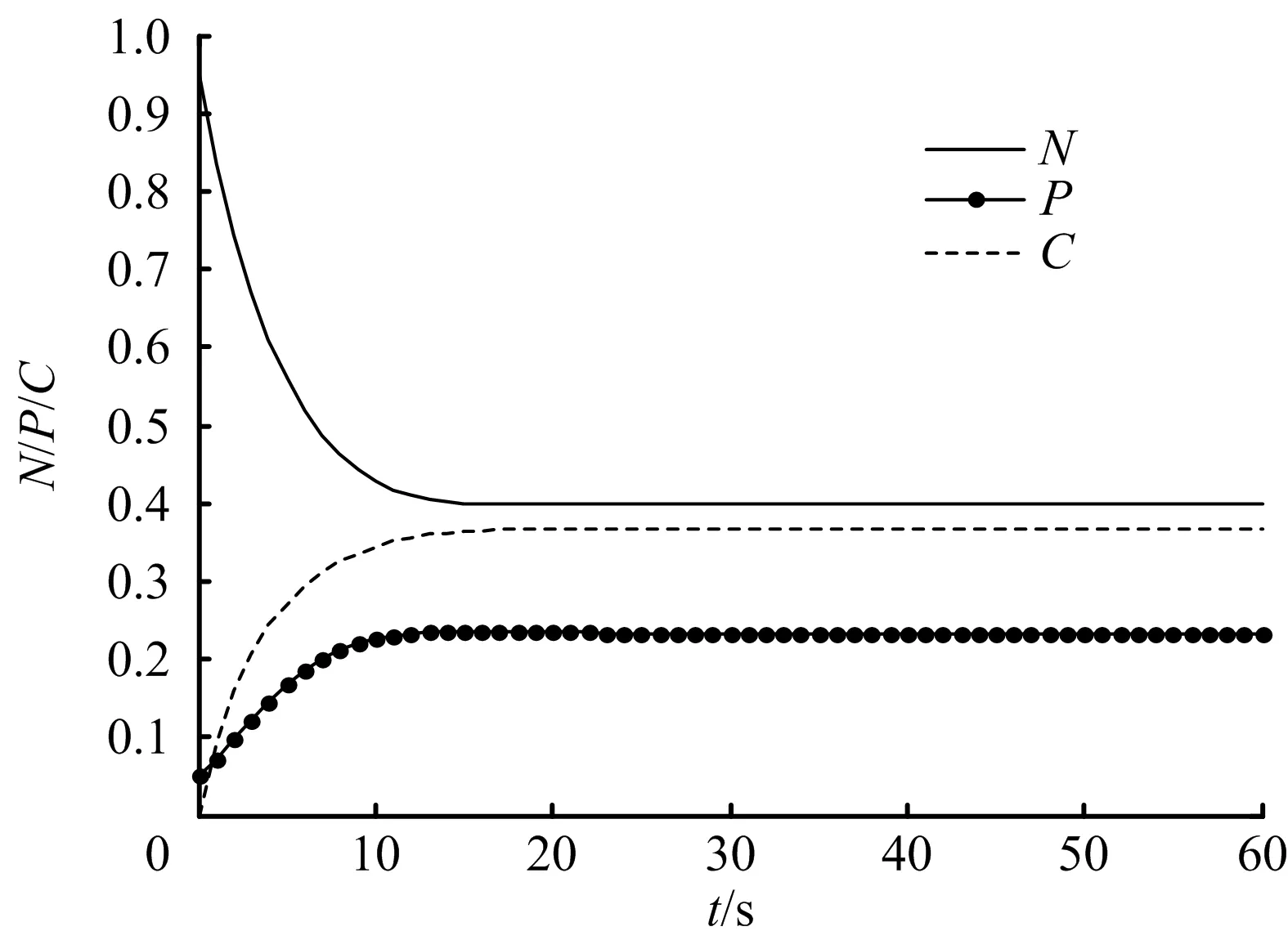
图4 改进模型的N、P、C动态变化

由图4可知，突发事件发生后恐慌人群比例P由初始值5%迅速上升至最大值23.56%，并最终趋于稳定值23.33%；正常人群比例N由初始值95%迅速下降并最终趋于稳定值40.00%；冷静人群比例C由初始值0逐渐上升并最终趋于稳定值36.67%。

对比图2与图4可知，图4中P值明显小于图2中P值，N、C均显著提高，加入干预因子后，图4P上升速度明显低于图2P上升速度，说明阻碍因子和促进因子对恐慌心理蔓延影响较大。一方面阻碍因子降低正常人群向恐慌人群转化概率以及冷静人群失去镇定状态转化为正常人的概率；另一方面促进因子增大恐慌人群向冷静人群转化概率以及正常人群获得理智转化为冷静人群的概率，最终使恐慌人群数量降低，恐慌心理蔓延速度减小，有效抑制恐慌心理蔓延。

分别改变ω和ψ取值，研究阻碍因子ω、促进因子ψ对模型影响。参数以图4各参数为基础设置，干预因子影响下P动态变化如图5所示。

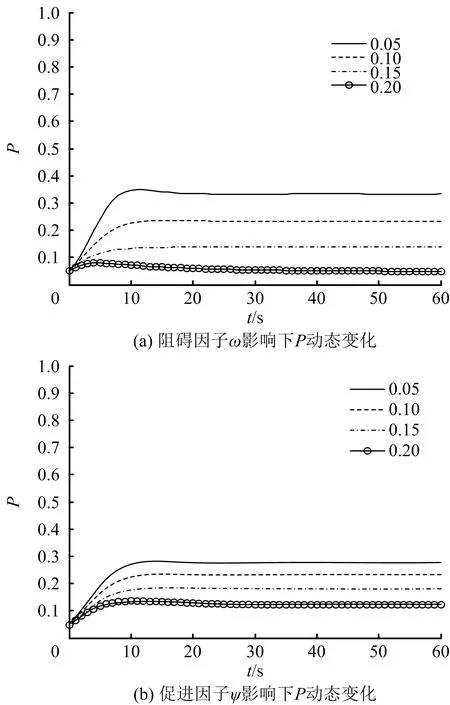
图5 干预因子影响下P动态变化

由图5(a)可知，阻碍因子ω越大，系统稳定后恐慌人群比例P越小，人群恐慌程度越缓和；由图5(b)可知，促进因子ψ对恐慌蔓延影响与阻碍因子ω影响效果类似；随干预因子ω与ψ增大，前者P的降幅大于后者，当ω=ψ= 0.2时，系统稳定后前者P为5%，后者P为12%。因此，相对于促进因子ψ，阻碍因子ω对模型影响更大。

4 结论

1)基础NPCN模型中，恐慌人群比例P随恐慌率α和冷静损失率γ增大而增大，随冷静率β增大而减小。

2)在阻碍因子ω和促进因子ψ作用下，模型稳定后恐慌人群比例P明显低于基础NPCN恐慌心理蔓延模型，说明及时采取干预措施可有效控制恐慌心理蔓延；干预措施越有力，恐慌心理蔓延抑制效果越明显。

3)通过控制变量法可知，相对促进因子ψ，阻碍因子ω对人群恐慌心理蔓延影响更大，且ω越大，抑制现象越明显。