矩阵特征值分解的算法研究与FPGA 实现
2021-08-20黄家俊王建新
黄家俊,王建新
(南京理工大学电子工程与光电技术学院,江苏南京 210094)
阵列信号处理中的一类典型问题是如何从接收到的多路观测数据中解析出被混叠着的原始信号[1]。常用的阵列信号分离算法有波达方向(Direction of Arrival,DOA)估计[2-4]、盲源分离[5]、快速独立成分分析(Fast Independent Component Analysis,FastICA)[6-9]等。这些算法都需要涉及大量的矩阵运算,而矩阵特征值分解就是其中的关键步骤之一。
常规的特征值分解算法主要针对实对称矩阵,如Jacobi 旋转法、QR 迭代法[10],其中Jacobi 法计算简单、精度高,应用更为广泛。传感器阵列观测到的信号经数字正交下变频后变成I/Q 两路的复信号,其协方差矩阵是一个复Hermitian 矩阵,无法直接应用传统的算法。所以需要通过一定的运算先将复Hermitian 矩阵转化为实对称矩阵。
FPGA 硬件相较于DSP 硬件,运行速度快,并行运算能力强,更适合解决阵列信号处理中的矩阵运算。因此,该文研究阵列信号处理中典型的复Hermitian 矩阵特征值分解问题,在FPGA 中实现矩阵转化和特征值分解的运算。
1 矩阵转化
假设由M个天线组成的天线阵列观测到的信号经正交下变频后得到的复观测数据为x(t),如式(1)所示。

其中,N为x(t)的采样长度。显然矩阵Rx是一个M×M阶的复Hermitian 矩阵。
复Hermitian 矩阵向实对称矩阵的转化有两种处理方法。第一种转化方法是将M×M阶的复Hermitian 矩阵转换为2M×2M阶的实对称矩阵[11],首先用实对称矩阵Rr和反对称实矩阵Ri作为实部和虚部来表示矩阵Rx。假设矩阵Rx的特征值σ对应的特征向量实部为u、虚部为v,可以得到下式:
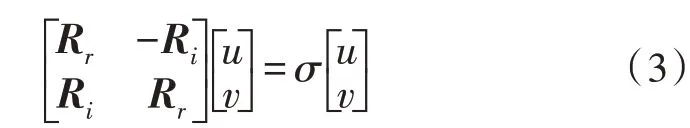
易证式(3)中的分块矩阵是实对称的。综上,M×M阶的复Hermitian 矩阵Rx的特征值分解等价于求解由实矩阵Rr、Ri组成的2M×2M阶分块矩阵的特征值分解。这种转化方法是严格等价的,没有误差。但是这种方法扩大了待求解矩阵的阶数,运算量大。
为了减少运算量,第二种转化方法将M×M阶复Hermitian 矩阵转化为M×M阶的实对称矩阵。定义一个M×M阶分块矩阵U,M为偶数时,结构如下:

定义满足如下等式的复Hermitian 矩阵P为中心对称的复Hermitian 矩阵:

不难证明可以通过下式将矩阵Rx转化为一个中心对称的复Hermitian 矩阵R[2,4]:
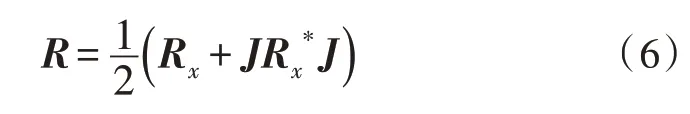
定义一个由矩阵R变换而来的Hermitian矩阵K:

综上,矩阵K是一个实对称矩阵。定义UK为矩阵K的特征向量矩阵,∑K为矩阵K的特征值矩阵,那么矩阵R的特征值分解可以表示为:
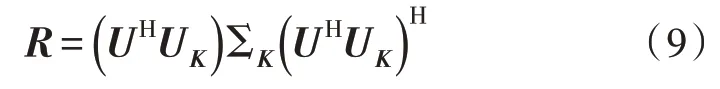
根据式(9)可以得到矩阵R的特征向量矩阵为UHUK,矩阵R的特征值矩阵就是∑K。
如果M为奇数,此时,矩阵U结构类似,矩阵I、J都是阶的,上述证明依旧成立。
综上,可以通过一定的运算将原本的复Hermitian 矩阵Rx先变换为一个中心对称的复Hermitian 矩阵R,再将矩阵R等价变换为一个实对称矩阵K。在求解K的特征值分解后得到R的特征值分解,从而替代Rx的特征值分解。第二种转化方法不扩大原矩阵阶数,计算量相较于第一种方法是大幅度减小的。当然这种转化并不是严格等价的,对于矩阵R和矩阵Rx之间的转化误差,可以证明在所有的复Hermitian中心对称矩阵中,矩阵R是对矩阵Rx在欧式距离(Euclidean Distance)下的最佳估计[12]。
2 Jacobi旋转法
Jacobi 法的基本原理为如果一个方阵是三角矩阵或对角阵,则该方阵主对角线上的元素就是该方阵的特征值。因此可以利用旋转矩阵不断地对实对称矩阵K进行正交相似变换,通过变换将方阵K中所有非主对角线元素都消去,在精度足够高的情况下,最后得到的近似的对角阵就是原矩阵K的特征值矩阵。矩阵K的特征向量矩阵也可以通过类似的运算来求得[13-14]。
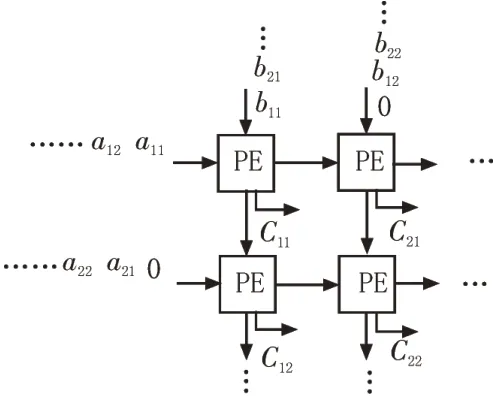
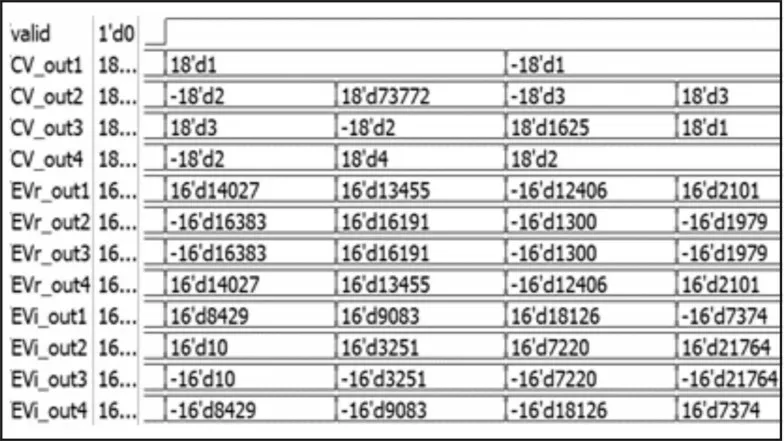
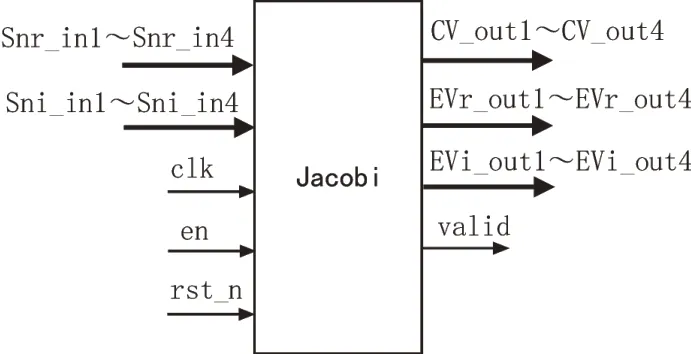
首先基于单位矩阵I定义一个M×M阶旋转矩阵Qij(1 ≤i 易证矩阵Qij是一个正交矩阵,令K0=K,利用旋转矩阵Qij对矩阵K0进行一次正交相似变换,得到矩阵K1: 变换后的矩阵K1仍然是一个实对称矩阵,设矩阵K1中第p行第q列(1 ≤p 1)当p≠i或j且q≠i或j时,变换前后的矩阵元素相等,不发生变化。 2)当p=i,q=j时: 3)当p=i或j,q≠i或j时: 为了提高效率,每次正交相似变化都应该消去矩阵上三角部分中绝对值最大的元素。定义实对称矩阵G的特征值矩阵CV、特征向量矩阵EV,利用Jacobi 旋转法求解矩阵G的特征值分解,一般步骤如下: 1)给矩阵CV和矩阵EV赋初值(矩阵CV初值为矩阵G,矩阵EV初值为单位矩阵I); 2)寻找矩阵CV上三角部分中绝对值最大的元素cvij,将其与允许误差ej进行比较,小于ej进行步骤6),否则进行步骤3); 3)根据元素cvij、cvii、cvjj的值计算旋转角θ; 4)计算旋转角θ的正余弦值,构造旋转矩阵Qij; 5)计算变换后的矩阵CV、矩阵EV,然后进行步骤2): 6)输出矩阵CV和矩阵EV。 Jacobi 旋转法的计算时间取决于两点:一是ej的大小,ej越小表明计算出来的特征值矩阵越接近对角阵,算法误差越小,需要的迭代次数就越多。二是待分解矩阵G的大小,G越大,待消去的元素数量越多,迭代次数也就越多,并且单次迭代时矩阵乘法的运算量也越大。 上一节的算法流程中,Jacobi 法的迭代次数不固定。在FPGA 中迭代次数不固定会导致时延的不确定,因此需要根据待分解矩阵的阶数以及数据的量化精度来固定迭代次数。对于ej而言,在FPGA 中会受到量化精度和计算精度的影响,过小的ej是无法达到的。根据仿真,16 位量化精度时,4 阶方阵需要15 次迭代;24 位量化精度时,6 阶方阵需要25 次迭代。 利用FPGA 实现Jacobi 法求解特征值矩阵时,需要解决两个问题:一是三角函数的计算,二是矩阵乘法的实现。 Jacobi 迭代法中三角函数的计算主要包括两个部分:一是利用反正切arctan 函数计算旋转角θ的值,二是计算旋转角θ的正、余弦值。这两步计算都可以采用ISE 软件中自带的Cordic IP 核来完成,计算精度很高。 Jacobi 法中每次迭代需要进行3 次矩阵乘法运算。虽然可以用式(12)~(17)来直接计算每个元素值,但每次消去的元素位置不固定,导致每个元素的表达式也不固定,不如直接通过矩阵乘法来计算旋转后的矩阵。在FPGA 中,可以采用脉动阵列(Systolic Array)的结构来构造矩阵乘法器[16-17]。脉动阵列由多个相同的处理单元(Processing Elements,PE)按照特定的规则互联而成。 首先对矩阵乘法进行拆分,设m×n阶矩阵C是由m×l阶矩阵A和l×n阶矩阵B相乘得到的: 其中,i=1,2,…,m;j=1,2,…,l。 不难发现每一个PE 需要一个乘法器和一个累加器来完成对应元素的计算。为了使整个运算过程流水线化,输入的数据需要在PE 间“流动”起来,所以每个PE 都要对两路输入数据做一个单位的延时输出来提供给下一级PE 进行运算[18]。综上,矩阵乘法器中PE 的框图如图1 所示。 图1 PE结构图 为了实现m×l阶矩阵A与l×n阶矩阵B相乘,需要m×n个这样的PE 来组成脉动阵列。每一个PE 的输出对应矩阵C中的一个元素,用脉动阵列实现的矩阵乘法器结构如图2 所示。 图2 脉动阵列矩阵乘法器结构图 上图输入数据中的0 表示对输入数据做一个时钟的延迟以匹配上一级PE 的延时输出。如果预先对输入数据流进行控制可以提高PE 的利用率,减少PE 的数量,从而节省乘法器和加法器资源。 在矩阵乘法运算后,要对结果进行截位,截位策略是保证未参与运算的元素值不发生变化。根据仿真结果,特征值矩阵需要提前进行位扩展,以保证矩阵对角线上的特征值不溢出[19]。 以16 位定点数量化后的4 阶复Hermitian 矩阵Rx为例,其实部为: 使用第二种矩阵转化方法后用Jacobi 旋转法求特征值分解,其中Jacobi 法的迭代次数为15 次,Matlab 软件中计算出的特征值矩阵CV如下: 在ISE 软件中编写好程序后,用Modelsim 仿真得到的特征值矩阵CVM和特征向量矩阵EVM,如图3所示。模块端口图如图4 所示。 图3 Modelsim仿真结果图 图4 模块端口图 其中,clk 为输入时钟端口,en 为模块输入使能端口,rst_n 为模块异步清零端口,Snr_in1~Snr_in4 是矩阵Rx实部输入端口,Sni_in1~Sni_in4 是矩阵Rx虚部输入端口,每一个端口输入待求解矩阵的一行数据;valid 端口为输出有效端口,计算结果输出时同步置高,CV_out1~CV_out4 是矩阵CVM的输出端口(特征值矩阵在迭代开始时就已经做了防溢出位扩展),EVr_out1~EVr_out4 是矩阵EVM实部输出端口,EVi_out1~EVi_out4 是矩阵EVM虚部输出端口。整个模块从数据输入到结果输出的延时为1 074 个时钟周期。由于Cordic IP 核的计算存在细小的误差,导致仿真结果与Matlab 定点仿真结果有一定的误差,不过对整体精度影响非常小。‖ ‖∙2表示对矩阵取二范数,Modelsim 仿真结果与Matlab 仿真结果的归一化误差为: 整个模块的资源消耗情况如表1 所示。 表1 FPGA模块资源消耗 该文对矩阵特征值分解算法进行了研究并给出了求解复Hermitian 矩阵的特征值分解的一般方案。该方案利用FPGA 完成复Hermitian 矩阵到实对称矩阵的转化后,再运用Jacobi 旋转法求解转化后的实对称矩阵特征值分解。整个方案具有结构简单、计算精度高、时延小、资源消耗少的特点。





3 Jacobi旋转法的FPGA实现
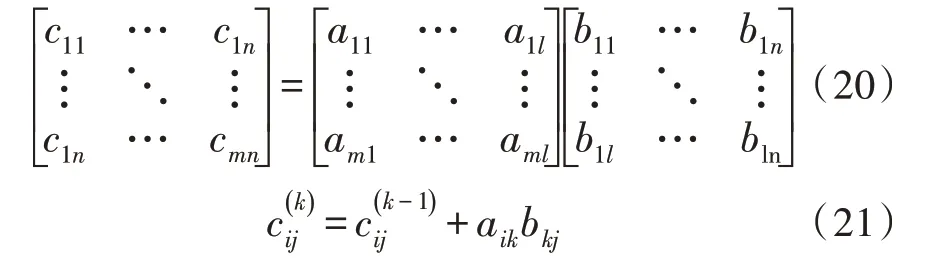

4 仿真结果




5 结束语
