磁悬浮辅助轴承用双层滚珠轴承性能分析
2021-08-20李欣龚高
李欣 龚高
1.广东省高速节能电机系统企业重点实验室 广东珠海 519070 2.珠海格力电器股份有限公司 广东珠海 519070
1 引言
磁悬浮轴承具备无润滑、无磨损、低噪声、低功耗等特点,适合应用于各类家用或商用电器当中[1-3]。在磁悬浮轴承系统中,辅助轴承是不可或缺的组成部件,起到临时支承、应急防护的作用,是整个磁悬浮轴承-转子系统安全可靠运行的基本保证。
由于采用磁悬浮轴承的转子往往高转速运行,一般远超过传统滚珠轴承的极限转速,此时在磁悬浮轴承失效后,辅助轴承将受到严重的冲击,同时转子与轴承之间剧烈摩擦,导致轴承的损坏。因此,提高辅助轴承的极限转速对于提高辅助轴承的可靠性具有重要意义。Prashad H提出了一种双层高精密轴承[4-5],转速将由两层滚动轴承来分配,以此提高轴承的工作转速,南京航空航天大学轴承研究所将其应用为磁悬浮系统的辅助轴承,并开展了相关研究[6-8]。目前对于双层轴承的研究以钢制滚珠轴承为研究对象,但针对高速转子跌落过程中产生的冲击及发热,钢制轴承的可靠性难以满足,仍存在应用限制。混合陶瓷球轴承因其自润滑、耐高温、耐腐蚀等优势[9],具有广阔的应用空间。将双层轴承与混合陶瓷球轴承相结合,并应用于磁悬浮系统辅助轴承,可有效提高辅助轴承的极限转速,进而提高其可靠性,但目前对此方面的研究仍有欠缺,需进一步深入研究。
为研究得到高可靠性的磁悬浮系统辅助轴承形式,本文将分析双层混合陶瓷球轴承的性能,首先以单层混合陶瓷球轴承为对象,分析磁悬浮轴承失电后高速转子跌落至辅助轴承后的轴承转速变化情况,再进一步基于轴承摩擦力矩平衡原理分析双层轴承相较于单层轴承的转速分配情况,并通过仿真对理论分析结果进行验证。本文通过对双层轴承的性能进行分析,验证作为磁悬浮辅助轴承的可靠性,对提高磁悬浮系统可靠性具有重要参考价值。
2 高速转子跌落至辅助轴承的动力学分析
磁悬浮转子系统包括电机组件、磁悬浮轴承及辅助轴承,在转子中心建立x-y-z坐标系,如图1所示,由于转子结构相对对称,因而可取其一半进行简化分析。
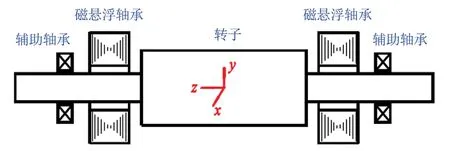
图1 磁悬浮转子结构示意图
当磁悬浮轴承失效时,转子自由落体至辅助轴承上,发生弹跳碰磨,最后带动辅助轴承内圈一起运动。此时,转子中心O(0,0)移动至O'(x,y)处,与轴承内圈之间发生接触,受到法向支持力Fn和切向摩擦力Ft作用,如图2所示。
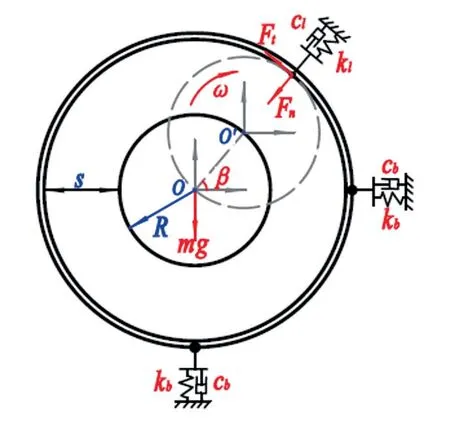
图2 转子运动及受力模型
转子半径为R,则转子与内圈的接触深度δ为:
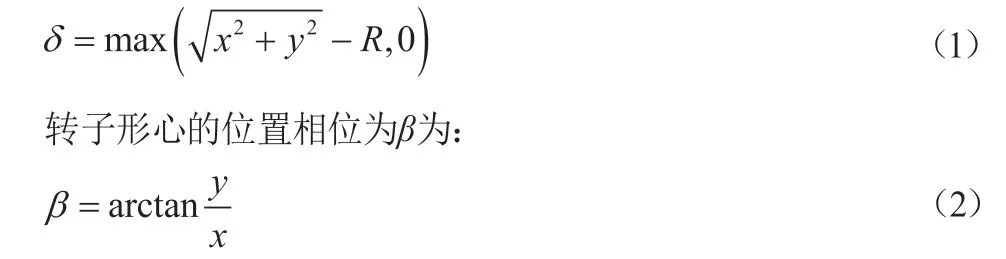
转子质量为mr,绕z轴的转动惯量为Jr,则此时转子动力学方程为:
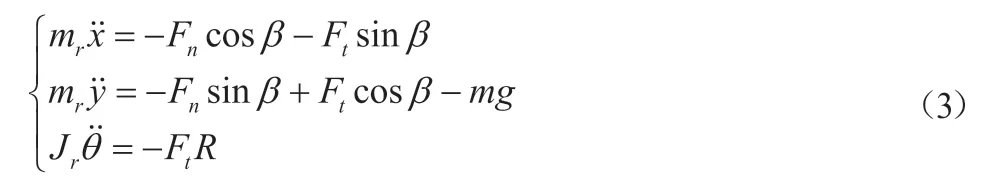
转子与轴承内圈的支持力Fn依Hunt-Crossley模型[10],Kl为转子与内圈的接触刚度,n为指数,对于线接触,取n=10/9,对于点接触,取n=1.5,α为转子与内圈的恢复系数,α=0.08~0.32 s/m。则法向支持力Fn为:

转子与轴承内圈的摩擦力Ft采用库伦摩擦形式,转子与内圈的滑动摩擦系数取为u,则摩擦力Ft为:

求解上述方程,得到转子初始转速250 Hz时跌落后转子及轴承内圈的转速情况如图3所示。
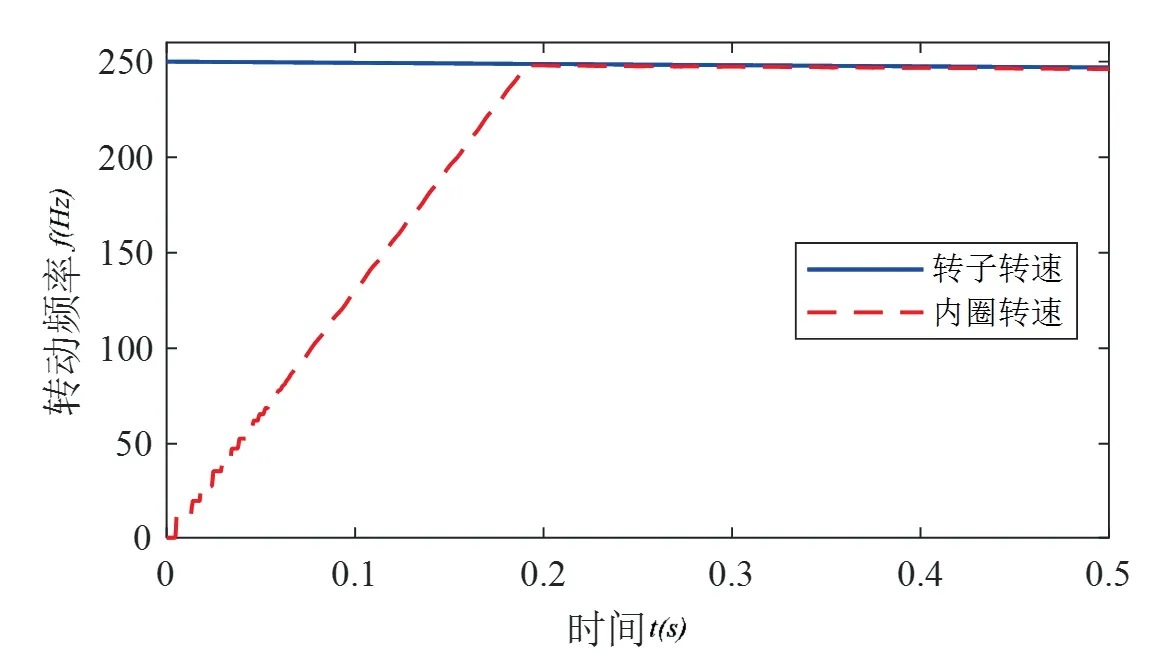
图3 转子及轴承转速-时间曲线
可以看出,跌落初始时内圈在极短时间内升频至与转子转速相同,随后与转子同步降速,且由于转子始终轴承内弹跳,内圈的运动状态较难稳定,始终在转子转频上下波动。
3 双层轴承转速分析
3.1 基于轴承摩擦力矩平衡计算双层轴承转速分配
根据帕姆格林的经验公式,总的摩擦力矩M可表示为[11]:

M0为与载荷无关的摩擦力矩,取Dpw为轴承节径,f0为与轴承种类和润滑有关的系数,η为润滑剂运动粘度,nb为轴承的工作转速,则M0为:
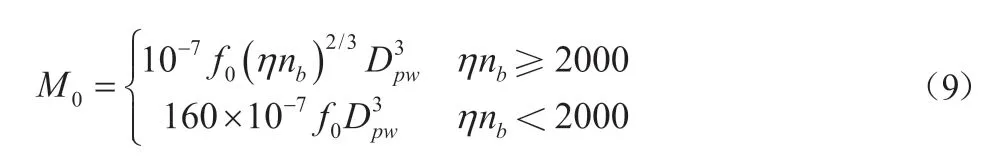
M1为与载荷相关的摩擦力矩,取f1为与轴承种类和载荷有关的系数,P为轴承负荷,则M1为:

基于上述方法,对双层轴承中间套圈受力分析,中间套圈受到内、外层滚动体的摩擦力矩分别为MZ1和MZ2,则得到中间套圈的力矩平衡方程为:

则将式(8)-(10)代入式(11),各参数增加下角标1、2分别对应内、外层轴承,nz为轴承中圈的工作转速,可得高速下双层轴承中圈摩擦力矩平衡方程为:
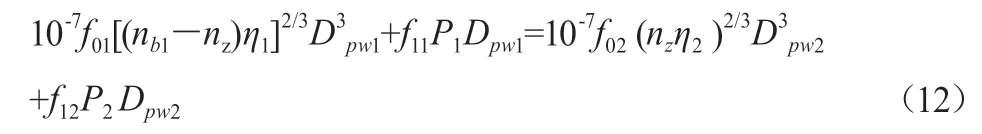
把总的平衡方程(12)作进一步分析:
(1)当润滑剂产生的影响较小,载荷占主导原因时,力矩平衡方程可以表示为:

(2)当载荷较小基本无影响时,润滑剂的影响占主导原因时,力矩平衡方程可以表示为:
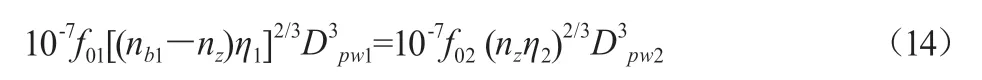
为简化分析,假设参数f0、η相同的情况下,根据式(14)可以得到双层滚动轴承的转速分配比:

根据文献[6]所述力矩M0对转速分配的影响更为突出,因此,在内、外层轴承参数f0、η相同的情况下,可采用式(15)对轴承的转速分配比进行计算,进而得到轴承中圈转速和轴承的极限转速情况。可以看出,此时双层轴承的转速分配比仅与内、外圈轴承的节径比值相关。
3.2 双层滚动轴承转速分配计算
以61812-61817组合双层轴承为研究对象,内、外层轴承基本参数见表1,双层轴承实物如图4所示。

图4 双层轴承结构
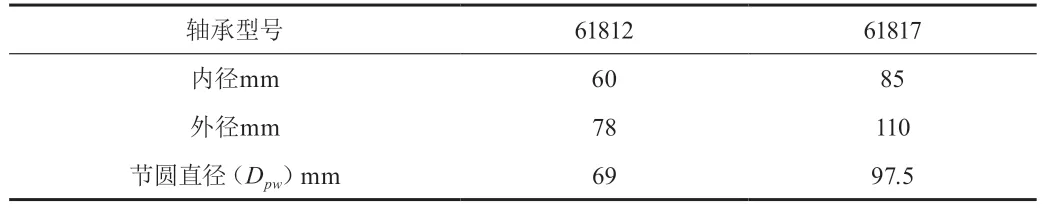
表1 双层轴承基本参数
由于内、外层轴承均采用深沟球轴承形式,且润滑条件相同,因此认为两组方程的参数f0、η相同,根据式(15),将Dpw1=69 mm,Dpw2=97.5 mm代入上式,得到转速分配比Ks为:
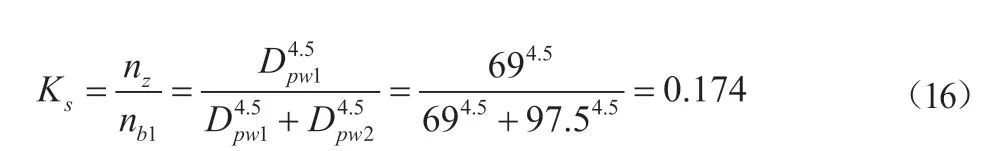
3.3 双层滚动轴承转速分配仿真
利用ADAMS软件对双层轴承的转速分配情况进行仿真,仿真过程主要包括模型建立、仿真设计、仿真运算及结果后处理几部分。
3.3.1 仿真模型建立
根据轴承的实际结构参数,包括各套圈内外径、滚珠直径、滚珠个数、沟曲率、沟底直径、轴承厚度等参数,建立双层轴承仿真模型,如图5所示。
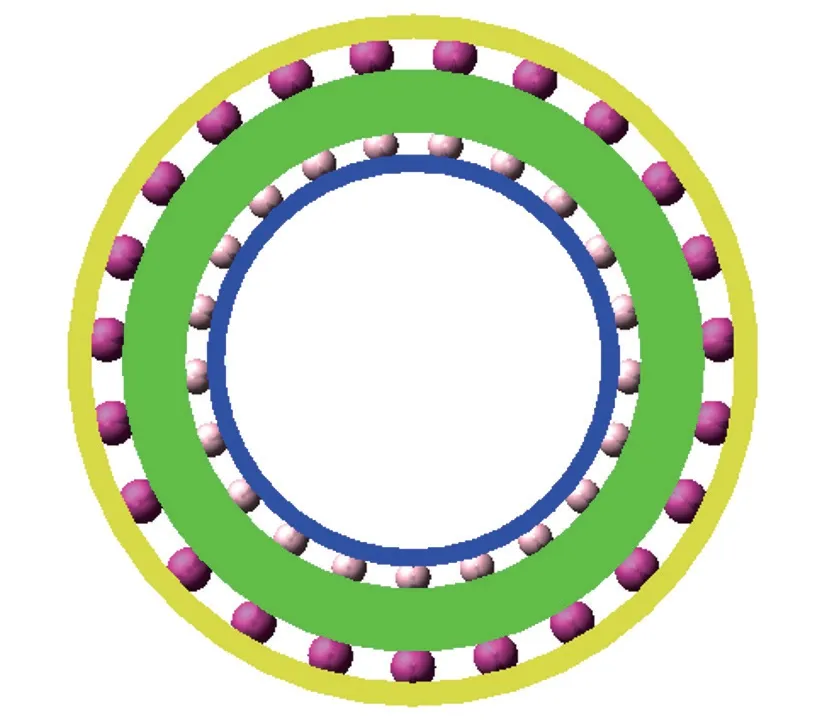
图5 双层轴承仿真模型
3.3.2 仿真设置
(1)材料设置
双层轴承采用混合陶瓷球轴承,套圈材料为轴承钢,滚珠材料为陶瓷Si3N4,按照材料实际参数进行设置。
(2)约束设置
模拟实际辅助轴承工作状态,外圈固定,内圈与转子接触并提供转速,因此设置外圈与大地固定连接。
转子与轴承内圈、滚珠与内外套圈之间设置为接触力。
(3)施加负载
在轴承内圈设置驱动转矩,为内圈转速施加转速。
3.3.3 仿真及结果分析
给定内圈转速为轴承的极限转速8500 r/min,仿真得到轴承内圈、中圈转速如图6所示。
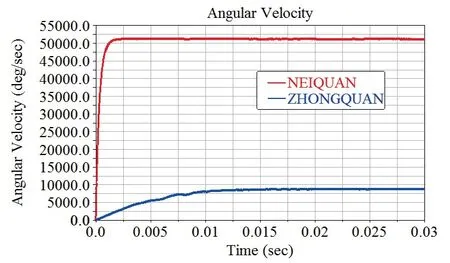
图6 轴承套圈转速(角速度/时间)
轴承内圈在0.002 s达到稳定转速,约51000 deg/s,即8500 r/min。
轴承中圈在0.015 s达到稳定转速,约8760 deg/s,即1460 r/min。
则此时轴承转速分配比为:

转速分配比的仿真结果与理论基本相同,极限转速提高Ks/(1-Ks)=21%。即现有常规混合陶瓷球轴承61812极限转速为8500 r/min,而改进的双层混合陶瓷球轴承61812+61817极限转速可提高21%,达到10285 r/min。
4 双层轴承可靠性试验
搭建磁悬浮辅助轴承抗跌落性能试验装置,如图7所示,对比双层混合陶瓷球轴承与常规混合陶瓷球轴承的可靠性。

图7 磁悬浮辅助轴承抗跌落性能试验装置
首先将电机升频至额定频率,稳定运行后同时切断电机及磁悬浮轴承电源,使高速转子跌落至辅助轴承上,比较辅助轴承可承受的跌落次数,实验结果见表2。

表2 辅助轴承抗跌落次数对比
通过试验可以发现,双层轴承较常规单层轴承抗跌落次数提高1倍以上。因此双层混合陶瓷球轴承通过提高极限转速,可有效地提升其作为辅助轴承的可靠性。
5 结论
常规滚珠轴承极限转速较低,难以满足磁悬浮系统辅助轴承的使用需求。为提高磁悬浮辅助轴承的可靠性,本文提出将采用陶瓷球的双层轴承结构应用于磁悬浮辅助轴承,并通过转子跌落动力学分析和双层轴承转速分析,验证了双层混合陶瓷球轴承在极限转速上的性能提升效果,得到如下结论:
(1)跌落初始时内圈在极短时间内升频至与转子转速相同,随后与转子同步降速;
(2)双层轴承转速分配比与内外层轴承节圆直径比、润滑情况、摩擦系数、负载有关,在无负载且润滑条件完全相同的情况下,转速分配比仅与节圆直径比有关;
(3)利用ADAMS进行双层轴承转速分配仿真可以与理论分析有较好的吻合,针对混合陶瓷球轴承61812,将其替换为双层混合陶瓷球轴承61812+61817,在极限转速附近且无负载情况下可以使极限转速提高21%。
