基于改进LSTM算法的短时交通流量预测
2021-08-20刘铭,鱼昕
刘 铭, 鱼 昕
(长春工业大学 数学与统计学院, 长春 130012)
0 引 言
及时准确的短时交通预测是智能交通系统中交通诱导、 事故检测、 交通分配的前提, 常见的短时交通流量预测方法可以简略分为以下3种: ①基于线性模型的方法。线性模型主要包括: 历史平均模型(historical average, HA)、 卡尔曼滤波模型(Kalman filtering, KF)及求和自回归滑动平均模型(autoreg ressive integrated moving average, ARIMA)。如Emami等将卡尔曼滤波模型应用到短时交通流量预测中[1], Kumar等使用季节性ARIMA模型进行交通流量预测[2], 并且取得了不错的预测结果。但从总体的预测结果来分析, 这类预测方法的大多数理论基础都是线性估计模型, 抗外界干扰能力差, 当交通流变化的随机性和非线性增强后, 模型的预测性能逐渐变差, 并且上述线性模型大多只考虑了交通流本身的规律, 没有考虑其他的因素(例如天气因素)。②基于非线性模型方法。非线性模型主要包括: 非参数回归预测模型、 神经网络预测模型以及支持向量回归预测模型等。如Carl等使用人工神经网络对短时交通流量进行了预测[3], Clark使用非线性回归模型预测短时交通流量[4], 欧阳俊等提出基于多核混合支持向量机(support vector machine, SVM)的预测方法[5]。从预测效果来看, 基于短时交通流非线性的特点, 相比线性方法, 非线性方法理论上更加适用, 它不需要线性方法的模型辨识和参数估计过程, 而是通过对历史数据进行学习推演。但是这种方法也有弊端, 一是由于只是根据历史数据训练, 从数据本身寻找演化规律, 没有涉及交通流的机理; 二是为了能够保证学习的效果和预测精度, 必须有大量的数据作支撑, 数据量越大运算量也越大, 并且这类方法数学计算较为困难。③基于混合模型方法。混合模型算法是指将两种或者两种以上的模型组合应用于短时交通流量的预测, 是目前国内外最流行的短时交通流量预测方法。如林静等将小波分析和贝叶斯估计组合对铁路货运量进行了预测[6], 提高了模型的精度;Ma等将SVM和循环神经网络(recurrent neural network, RNN)相结合进行交通流预测[7]; 杜金彪将K近邻算法 (Knearest neighbor, KNN)和径向基网络(radial basis function, RBF)相结合应用于短时交通流量的预测[8], 都取得了不错的预测效果。虽然混合模型可以将几种模型的优势互补, 相比于单一的预测模型拥有更高的预测精度, 但也增加了预测的计算量和复杂度。
近年来, 随着深度学习的发展, 其已被广泛应用于短时交通流量的预测中。如Koesdwiady等使用深度神经网络(deep neural network, DBN)算法研究了天气因素对于交通流的影响[9], 并以美国实际数据证明了算法的有效性。Zhao等使用单一的LSTM模型对15、 30、 45和60 min后的交通流量进行了预测, 虽然整体效果均优于传统模型, 但在15和30 min后的交通流量预测中精度的提升并不明显, 没有充分提取短时交通流量数据的时空特性[10]。Zhang等提出了一种基于CNN深度学习框架的短期交通流量预测模型[11], 通过卷积学习交通流量的特征, 从而建立预测模型, 并将预测结果与实际交通数据进行比较, 评估了该方法的有效性。
交通流具有不确定性、 周期性、 相关性、 非线性等基本的特征, 这决定了短时交通流预测不是单一的模型或者方法所能够解决或者完成的。上述模型都有自己的优缺点以及使用范围和条件, 因此混合方法在短时交通流预测中更具有优势。为了充分提高短时交通流量预测的准确率, 本文提出了一种基于改进LSTM的短时交通流量预测模型。
1 改进的LSTM模型
1.1 LSTM模型
Hochreiter等首次提出了LSTM算法[12], 它是递归神经网络的一种, 目前已被广泛应用到机器控制、 文本识别、 语音识别等领域。LSTM同其他神经网络一样, 也有相似的链式结构, 如图1所示。
其中,xt代表t时刻的输入,ht代表t时刻的隐藏层的状态,ot代表t时刻的输出,yt代表样本t时刻给出的实际值,lt代表t时刻的损失函数,W代表隐藏层上一个状态到下一个状态的权重,U代表输入层到隐藏层的权重。可知, 随着序列推进,“损失”也不断累积。除上述特点之外, LSTM中神经元之间权值共享, 即图1中的W、U是完全相同的。每个神经元都只与其本身的路线建立权连接, 不会与别的神经元连接, 与其他神经网络的不同之处在于, 它以图2这种特殊的重复结构进行神经元之间的交互。

图1 LSTM递归神经网络链式结构图
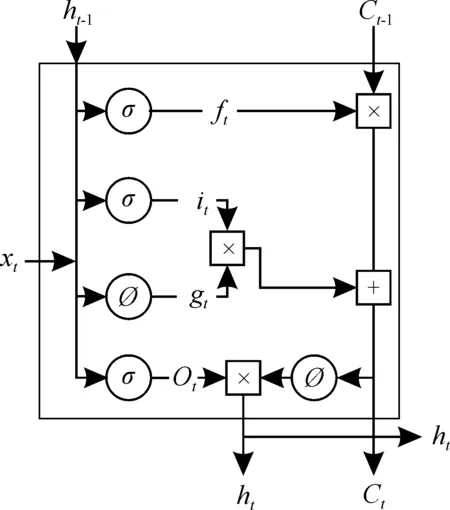
图2 重复模块结构图
通过3部分理解这种特殊方式。第1部分为过滤, 即在LSTM中以一定的概率过滤去除上一层的隐藏细胞状态。
ft=σ(Wf1ht-1+Wf2xt+bf1),
(1)
其中:σ为sigmoid激活函数,Wf1、Wf2为权重矩阵,bf1为偏置矩阵。
第2部分是输入部分, 整个输入部分可分为两个子部分it、gt。
it=σ(Wi1ht-1+Wi2xt+bi1);
(2)
gt=Ø(Wg1ht-1+Wg2xt+bg1)。
(3)
Ct=Ct-1ft+itgt,
(4)
其中,σ为sigmoid激活函数, Ø为tanh激活函数,Wi1、Wi2、Wg1、Wg2为权重矩阵,Bi1、Wg1为偏置矩阵,Ct-1代表t-1时刻的细胞状态。通过Ct更新细胞的状态。
第3部分为输出部分。先用sigmoid函数决定将要输出的细胞内容, 再通过tanh函数更新细胞状态, 两者相乘, 从而实现只输出想要输出的部分。
Ot=σ(Wo1ht-1+Wo2xt+bo1),
(5)
ht=Ottanh(Ct),
(6)
其中,Wo1、Wo2为权重矩阵,bo1为偏置矩阵。
1.2 算术平均滤波(mean-value filter, MVF)
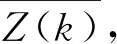
(7)
其实质是把n个采样值相加, 求其平均值, 作为t时刻的值。
1.3 MVF-LSTM模型
对于短时交通流量的预测, 影响因素较多, 例如: 道路交通管制、 车辆限行、 极端天气、 能见度低、 其他突发状况等, 交通流的变化极其复杂, 使得交通流的数据具有极强的噪声。原有的LSTM模型在预测时受交通流数据的极强噪声的干扰极强, 很难保证准确性。现对原有的LSTM模型进行改进, 提出一种MVF-LSTM模型, 其网络结构图如图3所示。

图3 MVF-LSTM模型网络结构图
MVF-LSTM模型在原始的LSTM模型的输入层之前加了算术平均滤波层, 经过算术平均滤波处理后特征加入到原始LSTM模型的输入层当中。即算术平均滤波是一个安插在LSTM输入层之前的计算单元, 能够过滤掉短时交通流量数据存在的噪声, 从而减少噪声数据对模型预测准确度的影响。则式(1)、 (2)、 (3)、 (5)变换为
(8)
(9)
(10)
(11)
2 基于MVF-LSTM模型的短时交通流量预测
2.1 实验设置
采用前文提到的MVF-LSTM模型预测交通流的数量, 所设计的MVF-LSTM网络结构包含算术滤波层、 输入层、 隐藏层和输出层各1个。其中隐藏层有9个神经单元结构。在训练中每次给网络中输入50组数据, 每组的时间步长为6, 整个网络的迭代次数设置为1 800。使用TensorFlow框架完成网络的搭建。在优化网络参数时, 选用动量梯度下降(Momentum)优化网络的参数。
2.1.1 数据来源 采用美国明尼苏达州的明尼阿波利斯和圣保罗之间94号州际公路西行每小时的交通量、 是否节假日、 天气、 气温等信息数据,数据来源于UCI(University of California Irvine)数据库(http: //archive.ics.uci.edu/ml/index.php)。 图4所示为94号州际公路的概况。

图4 94号州际公路的位置
2.1.2 预测结果性能评价性指标 为了对LSTM模型在交通流量预测中的性能进行评价, 本研究采用平均相对误差MAPE和均等系数EC作为评价指标:
(12)
(13)
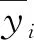
2.2 结果分析
以明尼阿波利斯和明尼苏达州圣保罗之间94号州际公路西行2016—2018年的每小时交通量为数据基础进行仿真实验。数据的时间间隔为1 h。现以仿真数据中的80%作为训练集, 后20%数据作为测试集, 进行模型参数的寻优并进行交通流量的预测, 寻找最佳的参数。
为了验证MVF-LSTM模型的优越性, 本文同时还采用了支持向量回归(SVR)、 门控循环单元(GRU)神经网络、 深度神经网络(DBN)、 卷积神经网络(CNN)、 长短期记忆网络(LSTM)与本文的MVF-LSTM模型进行对比, 结果如图5所示。

图5 各种模型预测结果对比
SVR的预测结果和原始交通流量的误差相对较大, 尤其在峰值点处, 预测趋势会出现滞后的现象。GRU模型的预测结果虽然在预测的趋势上和真实趋势相吻合, 但在峰值和拐点处预测偏差较大。DBN模型和CNN模型虽然相较于SVR和GRU模型的预测结果稍好, 但在峰值处的预测也相对较差。从LSTM模型预测的结果来看, 虽然模型的泛化能力比较好, 但峰值预测的精度上存在一定的偏差。MVF-LSTM模型在原始LSTM模型的输入层加入算术平均滤波后, 滤掉了交通干扰噪声, 预测出的交通流量的趋势和真实趋势吻合度比较高, 在峰值处预测值和真实值也十分贴近。各模型的精度如表1所示。

表1 模型预测性能比较
可见, MVF-LSTM模型的MAPE值比SVR、 GRU、 DBN、 CNN和LSTM模型的都小, 表明MVF-LSTM模型的预测值最贴近真实值, 预测的准确度更好。本文改进后的新方法EC值增大, 说明增加了模型的稳定性, 减少了真实值和预测值的分散程度, 从而获得了更好的预测效果。通过分析比较本文提出的MVF-LSTM模型在短时交通流量的预测中泛化能力更好, 相比于其他模型取得了较高的精度, 较原始的LSTM模型MAPE值提升了6%。
2.3 MVF-LSTM模型参数调优的比较分析
2.3.1 迭代次数对模型准确度的影响 由图6可以看出, 在前1 000~1 500次迭代中,MAPE值迅速下降; 1 500~1 800次,MAPE值缓慢下降, 代表模型的准确率通过迭代次数的增加在缓慢上升; 直到1 800次以后,MAPE值随训练次数增加而增大, 模型的预测误差再次上升。故选取1 800次作为本研究的模型迭代次数。
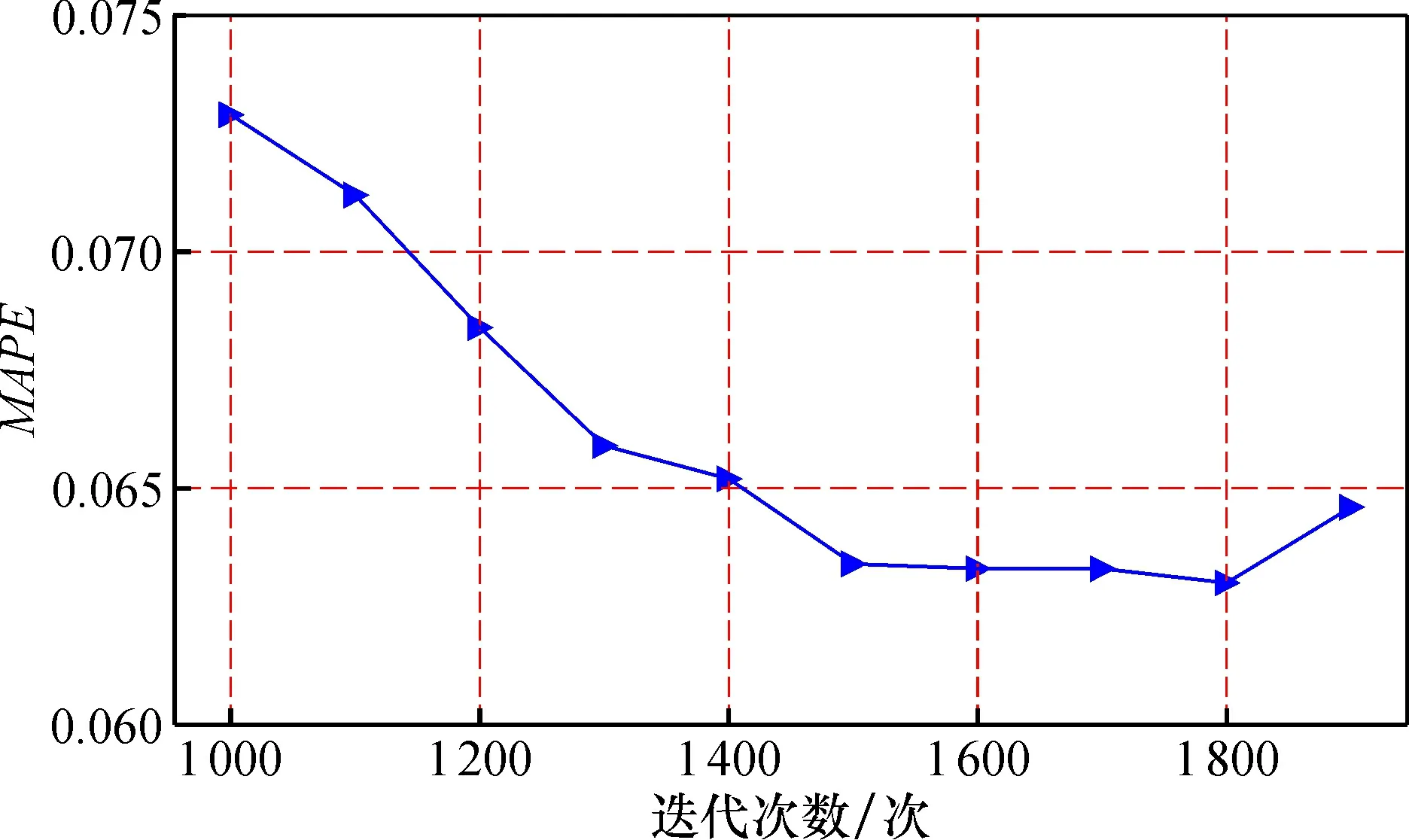
图6 不同迭代次数对模型准确度的影响图
2.3.2 时间步长对模型准确度的影响 从图7可以看出,MAPE值随着时间步长的增加呈现起伏的状况, 当时间步长取6个时,MAPE值最小。

图7 不同的时间步长对模型准确度的影响
3.3.3 隐藏层的神经元的个数对模型准确度的影响 如图8所示, 随着模型隐藏层神经元个数的上升,MAPE值出现了往复震荡的状况。 当隐藏层神经元的个数为9时,MAPE值达到最小, 所以最终MVF-LSTM模型的隐藏层神经元的个数设置为9。

图8 不同隐藏层神经元的数量对模型准确率的影响
3 结 论
本文提出的MVF-LSTM算法是本文短时交通流量预测研究的核心算法。利用算术平均滤波去除交通流量数据中的干扰噪声, 从而增加MVF-LSTM模型输入层的维度, 然后放入MVF-LSTM模型的隐藏层进行模型的训练, 通过模型去学习交通流量的特征, 从而学习到交通流量时间序列的本质特征, 并对交通流量进行了有效的预测。通过预测的评价指标, 与其他常用模型进行了分析比较, 验证了本文提出的MVF-LSTM模型对交通流量的预测精度很高, 并且具有很好的泛化能力, 对短时交通流量数据的预测具备一定的参考价值。但本文算法仍存在一些不足: 该模型虽然去除了交通流数据中的部分噪声, 但去噪效果的优劣主要取决于算术平均滤波层采样值个数的准确选择, 如何选取合适的采样值个数, 有待今后进一步的研究。
