降雨条件下非饱和土边坡渗流-应力耦合分析
2021-08-20吕雨桦梁德贤
吕雨桦, 梁德贤, 王 莹, 黄 翔
(桂林理工大学 地球科学学院, 广西 桂林 541006)
自然环境中边坡土体大多数处于非饱和状态, 非饱和土由于基质吸力的存在, 其抗剪强度较高, 使边坡处于稳定状态。受降雨入渗影响, 非饱和土的体积含水量增加, 力学强度显著降低, 进而导致滑坡的发生, 如千将坪滑坡[1]、 东乡县何坊村滑坡、 陈家湾沟滑坡[2]、 水城县滑坡等, 均揭示了降雨入渗是导致非饱和土边坡失稳的主要因素之一。
针对这一问题, 以往是先分析降雨入渗引起坡体内部渗流场的变化, 再结合极限平衡法或有限单元法来研究边坡稳定性[3-6], 忽略了土-水之间的相互影响。降雨入渗边坡岩土体的实质是渗流作用下渗流场与应力场耦合作用, 双场的影响具有相互性、 可逆性。目前, 双场耦合分析主要分为两大类: 一是间接耦合法, 先将两场分开计算, 通过两场的交叉迭代达到耦合目的[7-8]; 二是直接耦合法, 以渗流场与应力场为未知值建立数学模型, 求得解析解来达到完全耦合目的[9-12]。对于土体而言, 直接耦合法通常是基于Biot固结理论, 该方法无需进行两场的反复迭代, 只需有限单元法求解即可得到全部结果, 具有简单、 直观的特点。同时, 边坡变形过程本质上是其内部渗流场和应力场直接耦合的结果, 因此本文选用直接耦合法分析边坡稳定性问题更具实际意义。
为此, 本文以广西兴业县洛阳滑坡为研究对象, 基于非饱和土流固耦合理论及有限元极限平衡原理, 通过Geo-Studio有限元数值分析软件建立非饱和土边坡数值模型, 对非饱和土边坡渗流场、 应力场、 变形场进行直接耦合分析, 并在此基础上研究非饱和土边坡稳定性演化规律。
1 耦合原理及基本方程
降雨入渗边坡是典型的非饱和流固耦合现象, 其耦合原理: 降雨入渗使得渗流场以渗透力的形式改变原有的应力场, 而应力场的变化则通过体积应变、 孔隙比的变化来改变土体渗透系数, 从而影响土体的渗流场[13]。Geo-Studio软件求解过程是以位移增量和孔隙水压力增量为场变量, 依据初始条件、 边界条件将平衡方程与渗流方程同时求解的过程。
1.1 非饱和土本构方程
根据毕肖普有效应力原理, 非饱和土应变-应力增量形式可表示为[14]
Δσ=DΔε-DmH(ua-uw)+Δua,
(1)
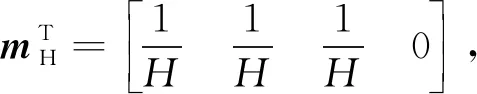
式中: Δσ为应力增量; Δε为应变增量;D为本构矩阵; Δua为孔隙气压力矢量增量;H为与基质吸力(ua-uw)有关的非饱和土模量(ua为孔隙气压力,uw为孔隙水压力)。假设孔隙气压力恒等于大气压力, 上式可表示为
Δσ=DΔε+uwDmH。
(2)
1.2 有限元本构方程
当只有一个点荷载F施加于系统时, 虚功方程为
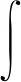
(3)
式中:ε*为虚应变;δ*为虚位移;σ为内应力。
将式(1)代入式(3)进行数值积分, 则有限方程可写为
∑BTDBΔδ+∑BTDmHNΔuw=∑F;
(4)
K=BTDB;Ld=BTDmHN,
式中: Δδ为位移矢量增量; Δuw为孔隙水压力矢量增量;B为应变矩阵;K为刚度矩阵;Ld为耦合矩阵;N为形函数行矢量。化简式(4)可写成
KΔδ+LdΔuw=F。
(5)
1.3 渗流方程
基于达西定律, 通过一个单元体积土体的二维渗流方程为[13]
(6)
式中:kx、ky分别为x和y方向的渗透系数;γw为单位水的容重;θw为体积含水量;t为时间。基于虚功原理, 渗流方程可以表示为孔隙水压力和体积应变的形式, 则得到有限元方程为
(7)
式中:Kf为单元刚度矩阵;MN为质量矩阵;Lf为渗流耦合矩阵;Q为边界节点的渗流。联立平衡方程(5)与渗流方程(7)可得有限元分析的耦合方程, 通过相应的边界条件即可对该耦合方程进行求解。
2 工程概况
洛阳滑坡位于广西兴业县洛阳镇政府后山, 属构造侵蚀—剥蚀丘陵地貌, 自然坡度22°~33°。如图1所示, 滑坡平面形态为“簸箕形”, 主滑方向295°, 滑体平均坡度约35°, 轴线长度150 m。前缘高程105 m, 后缘高程155 m, 相对高差为50 m。滑坡后缘发育多条弧形裂缝如图2a所示, 主缝两侧垂向错距0.3~1.0 m; 坡中部横向张性裂缝发育, 表面局部呈陡坎状, 少量树木歪斜(图2b)。
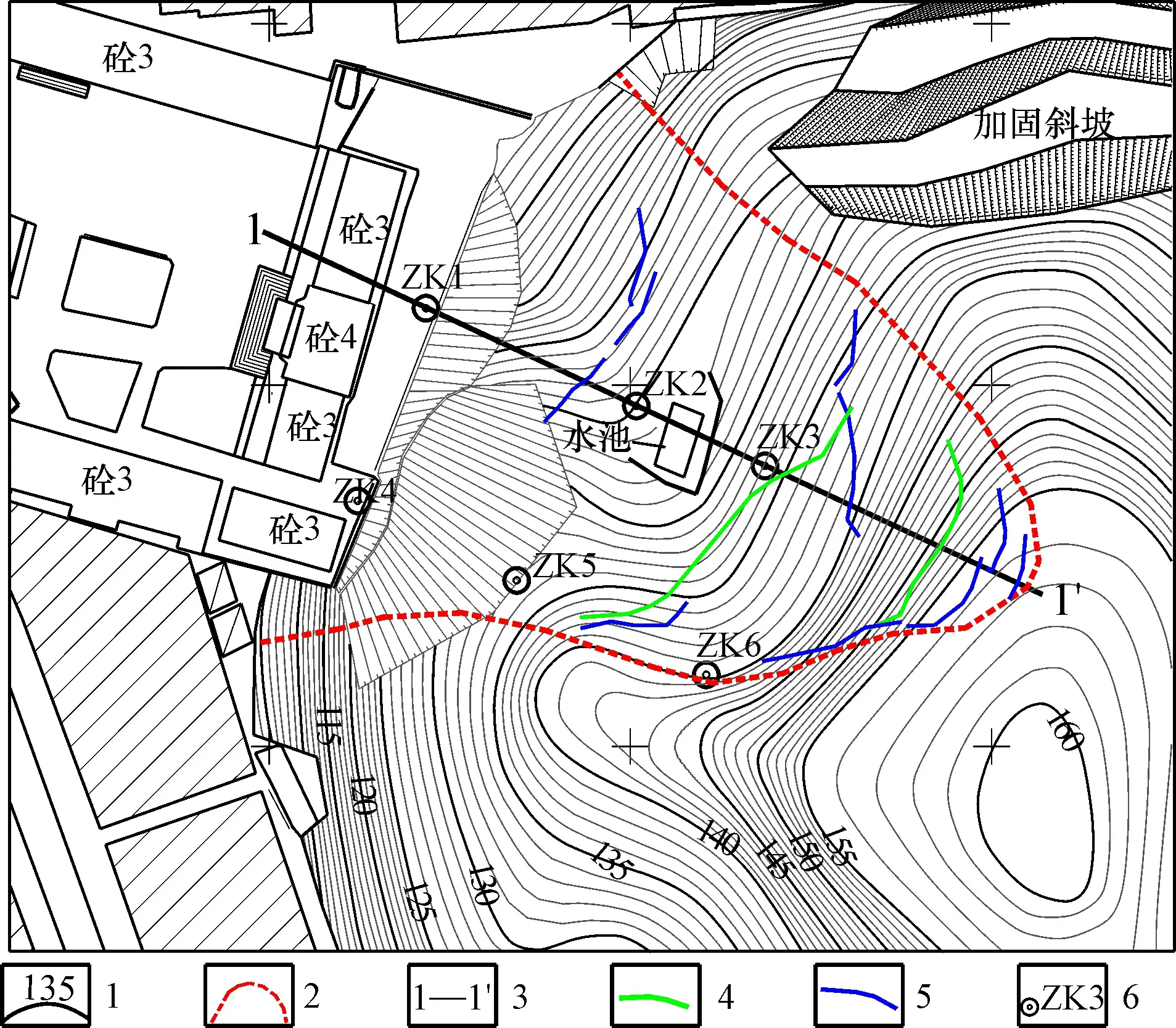
图1 滑坡平面图

图2 滑坡宏观变形迹象
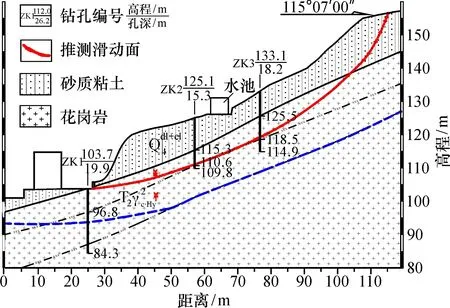
图3 滑坡1—1′剖面图
3 降雨条件下边坡渗流-应力耦合分析
选用Geo-Studio中的SEEP/W、 SIGMA/W、 SLOPE/W三种模块相互结合的方式进行渗流-应力耦合分析。利用SEEP/W模块从土-水特征曲线入手, 建立基质吸力与渗透系数的关系, 计算初始渗流场, 以文件形式保存, 作为SIGMA/W模块初始条件; 选用SIGMA/W模块耦合应力/孔隙水压力选项, 进行两场耦合分析, 得出各时步的渗流场、 应力场及位移场的计算结果; 将节点水头信息、 应力数据导入SLOPE/W模块, 采用有限元法对边坡稳定性进行动态分析。
3.1 模型构建及边界条件
根据滑坡地质原型和工程地质条件, 本文选取1—1′地质剖面建立数值模型。模型分为4层: ① 第四系残坡积层, ② 全风化花岗岩, ③ 强风化花岗岩, ④ 中风化花岗岩。有限元网格模式采用四边形和三角形进行划分, 共计1 022个节点、 966个单元, 如图4所示。初始渗流边界条件: 模型两侧地下水位以上部分及底部边界为零流量边界, 左、 右侧总水头分别为94、 128 m; 浸润线主要沿基岩分布, 坡脚处趋于水平分布。瞬态渗流边界条件: 模型坡面为单位流量边界。位移边界条件: 约束模型两侧的水平位移, 约束模型底部水平和竖向位移。为了更加方便分析降雨过程中边坡失稳的内在规律, 选取特征点A~G进行分析研究。
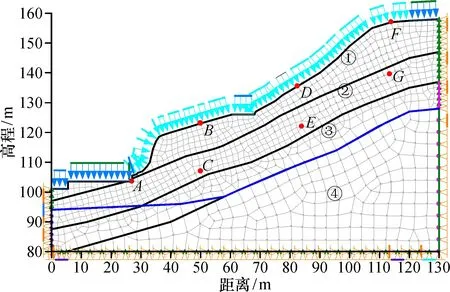
图4 计算模型
3.2 参数选取及模拟方案
模型介质为理想弹塑性材料, 服从莫尔-库伦强度准则, 物理力学性质参数见表1。运用SEEP/W模块自带的样本函数拟合得出各岩土体的土水特征曲线图5; 已知饱和渗透系数及土水特征曲线, 可依据Van Genuchten模型估算渗透系数曲线图6。

图5 土水特征曲线
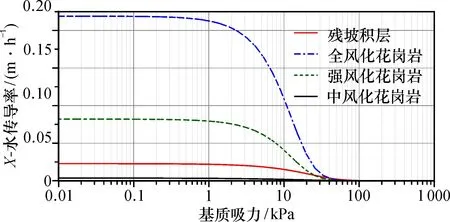
图6 渗透系数曲线

表1 岩土体物理力学参数取值
根据现场降雨状况及当地降雨数据, 模拟大暴雨(150 mm/d)工况下边坡渗流场、 应力场的变化。图7a为降雨强度与时间的关系, 降雨强度先随时间线性增加至最大值, 稳定15 h后线性减小为0, 整个计算时长为72 h, 其中, 降雨时长为45 h, 累计降雨量为187.5 mm。当降雨强度为6.25 mm/h, 设置坡脚水平面、 顶面降雨入渗6.25 mm/h, 坡面降雨入渗强度为6.25cos35°=5.2 mm/h。入渗强度随降雨强度变化而变化, 详见图7b。
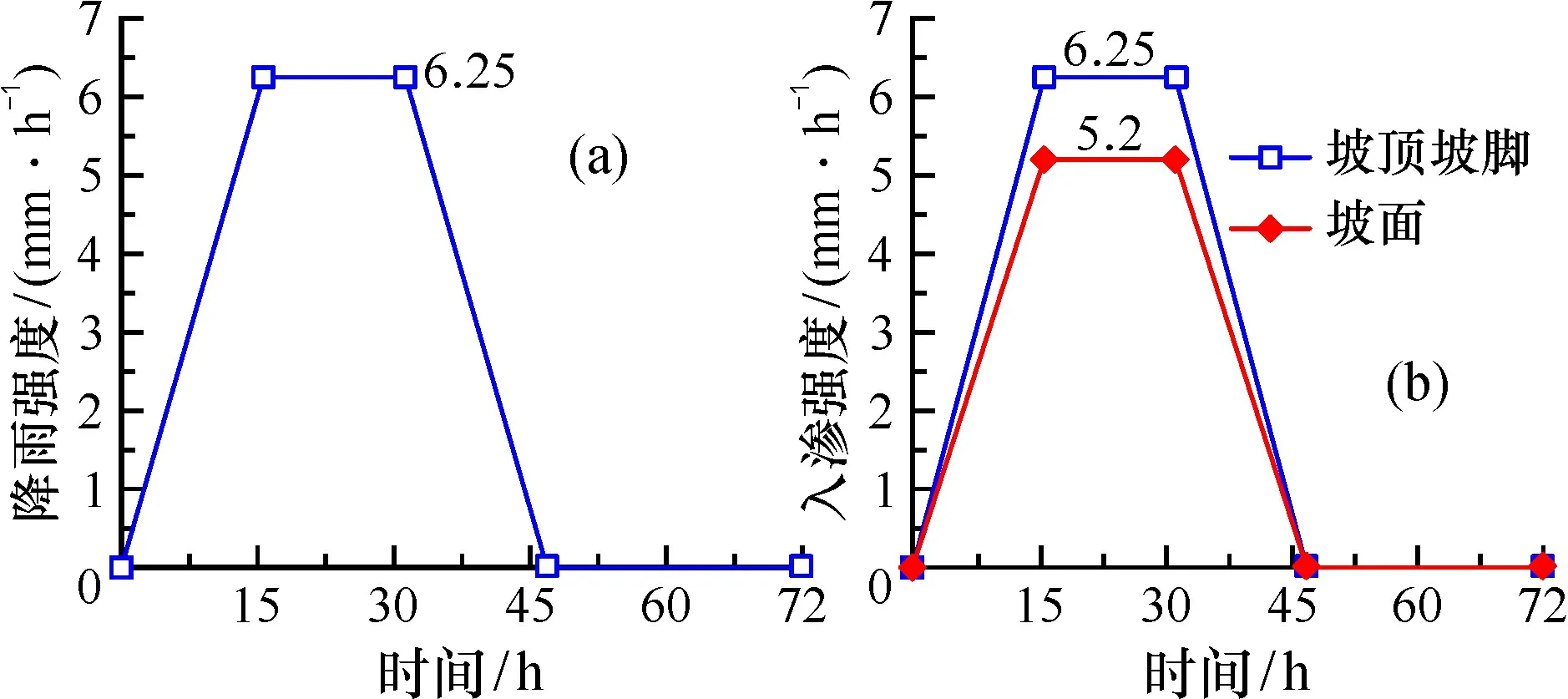
图7 降雨强度与入渗强度随时间变化
3.3 渗流场数值分析
图8为模拟过程中边坡孔隙水压力分布演化。总体上, 浸润线以上的非饱和区, 负孔隙水压力随着高程的增加而增大, 结合土-水特征曲线可知, 负孔隙水压力与体积含水量呈反比关系, 距离浸润线越近负孔隙水压力越小, 反之越大。随着降雨入渗, 非饱和区域不断减小, 饱和区域逐渐增大。在接近坡面位置处等值线密集, 负孔隙水压力持续降低; 坡顶处等值线闭合, 由外到内孔隙水压力等值线呈现高→低→高的现象, 主要是因为边坡表层土体最先对降雨作出响应, 而下部土体还未作出响应所致。降雨未对深处浸润线造成影响。
图9a为特征点A~G孔隙水压力随时间变化曲线。 0~15 h降雨强度持续增长, 坡体表层土体孔隙水压力最先对降雨作出响应, 特征点A、B、D、F孔隙水压力显著增长, 其中点F增幅最大, 且接近饱和状态; 15~30 h降雨强度持稳, 点F孔隙水压力回落, 点A、B、D孔隙水压力线粘合, 增幅放缓, 表明此阶段边坡表层土体中的水分有向坡脚开始迁移的趋势; 30~72 h降雨强度线性减小至降雨停止后, 整体上, 孔隙水压力出现回落减小态势, 减幅较小, 72 h(雨停后27 h)孔隙水压力依然没有完全消散的滞后现象, 如图8d。坡体内部特征点C、E、G孔隙水压力基本不变, 与边坡表层土体反应迅速、 反应剧烈形成鲜明对比。图9b为特征点A~G体积含水量随时间变化曲线, 与孔隙水压力变化具有相似的规律。边坡表层土体体积含水量与降雨强度呈正相关关系, 坡体内部基本不受降雨影响。浅层土体的体积含水量持续增长至30 h达到最大值, 30~72 h发生回弹现象。根据非饱和土力学理论可知, 非饱和土体基质吸力对边坡稳定性产生积极的影响, 而随着降雨的持续进行, 非饱和区体积含水率增加, 导致负孔隙水压力减小, 即基质吸力降低, 基质吸力对土体抗剪强度的贡献随之减少, 影响边坡的稳定性。自然环境中, 非饱和土边坡基质吸力在旱季升高, 雨季降低, 土体强度劣化, 致使滑坡灾害的发生。

图8 非饱和土边坡孔隙水压力分布演化
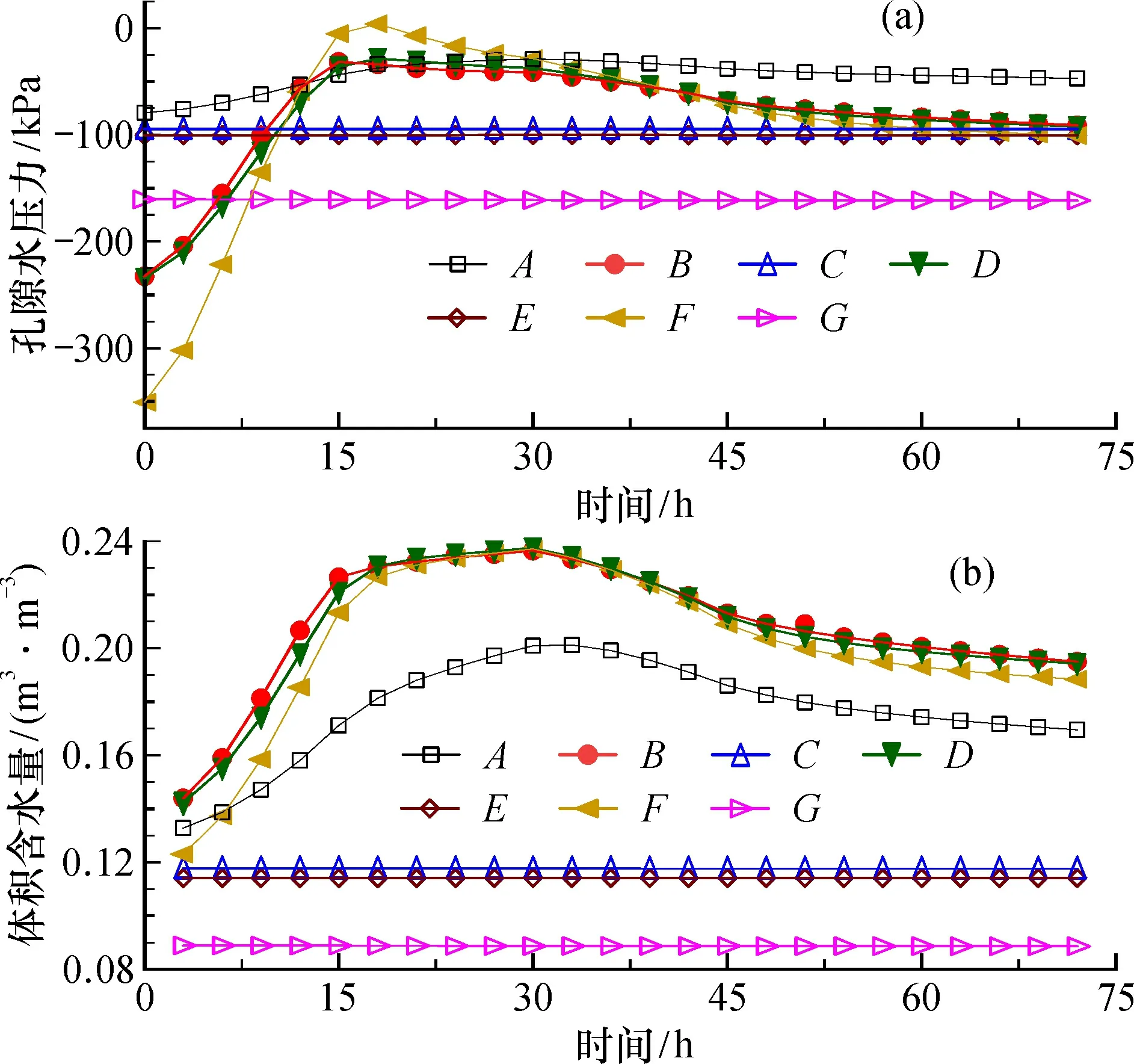
图9 特征点孔隙水压力与体积含水量随时间变化
3.4 应力场数值分析
图10为降雨前、 雨停后3 h最大剪应力等值线。剪应力分布整体上呈从坡面向坡内逐渐增大的趋势。降雨后, 边坡表面土体最大剪应力增大, 且坡脚处剪应力集中区范围增大, 特征点A的剪应力由140 kPa增至160 kPa; 坡面中上部出现新剪应力集中带, 表层土体的剪应力明显提高至140 kPa。应力集中区通常是滑坡发生剪切破坏最有利的部位, 可见坡中上部及坡脚处易发生剪切破坏。

图10 非饱和土边坡最大剪应力等值线演化
渗流场引起孔隙水压力变化, 破坏了其原始应力平衡状态, 引起有效应力变化, 如图11所示。0~30 h降雨强度增大至定值, 坡面点B、D、F的有效应力大幅度降低, 其中坡顶处点F降低幅度最大; 30~72 h降雨强度减小至雨停一段时间内, 坡面处有效应力发生少量回弹。基于Fredlund非饱和土抗剪强度理论, 有效应力减少对非饱和土抗剪强度产生消极影响。

图11 特征点有效应力随时间变化
由于有效应力降低, 边坡表层应力场改变, 产生变形响应, 主要体现为各土单元产生一定的位移, 如图12所示。特征点水平、 竖向位移在降雨作用下均呈增加的态势, 浅层土体位移变化幅度较大。特征点F竖向位移变幅最大, 约是其水平位移的3倍, 主要因为坡顶土体吸水, 在竖直方向发生膨胀, 产生竖向变形; 特征点B的水平位移增长速率最快, 竖向位移仅次于F点, 这是由于坡体前缘较陡, 缺少临空面方向的约束, 易产生水平位移, 导致小规模的土体滑塌; 特征点A仅发生水平位移, 降雨导致边坡土体的自重增大, 继而滑动力增大, 该滑动力传递于边坡下部对坡脚处产生挤压作用, 向边坡临空面产生水平变形, 可见坡脚处在降雨作用下易出现滑动失稳现象。

图12 特征点位移随时间变化
图13为72 h位移等值线, 位移分布由坡内向坡外逐渐增大。降雨大量入渗主要发生在浅层土体, 体积含水量增大, 浅层土体基质吸力、 有效应力降低, 应力场的变化引起浅层土体相对深层土体更大的变形。位移量持续变化使得坡体处于持续运动的状态, 当位移达到一定值, 坡体发生严重的变形破坏。前缘土体缺少水平方向的约束力最先破坏, 之后临空面上部土体因失去下部土体的支撑而导致滑塌失稳, 出现更大规模的滑坡灾害。结合现场调查, 滑坡后缘处有多条拉张裂缝, 坡面局部呈陡坎状, 判断此次滑坡为牵引式滑坡。

图13 72 h X-Y位移等值线
3.5 边坡稳定性演化分析
有限元极限平衡法是将边坡有限元应力分析结果与极限平衡法相结合进行边坡稳定性分析的方法。该方法避免了传统极限平衡法中的许多假设, 既能考虑边坡岩土体变形对稳定性的影响, 又能给出明确的稳定系数及破坏面。本文选取该方法对边坡进行稳定性演化分析, 其原理是以有限元计算的应力分布结果为基础, 通过应力张量变换, 求出指定滑动面上的应力分布, 结合极限平衡法计算公式, 求解出该滑动面的稳定系数[15]。
选取SLOPE/W模块SIGMA/W应力分析类型, SIGMA/W模块计算出的应力值、 孔隙水压力值为模拟基础, 对滑坡稳定系数变化及危险滑移面的位置进行探讨。边坡稳定系数随时间变化的关系曲线如图14所示, 降雨期间(0~45 h), 稳定系数随降雨强度增大而缓慢降低; 降雨强度维持最大值至减小为零的阶段(15~45 h), 稳定系数呈迅速衰减的态势; 降雨停止后(45~72 h), 稳定系数继续下降一定幅度再回升, 源于降雨入渗具有滞后性, 随着时间的推移, 孔隙水压力逐渐消散, 基质吸力上升增强土体的抗剪强度, 致使稳定系数回弹。边坡稳定系数最小值为0.997出现于54 h, 此时危险滑移面的位置如图15。结合图3所示实际滑移面的位置, 与通过数值模拟计算所得危险滑移面位置非常接近, 且与现场调查中滑坡后缘下错位置、 前缘剪出口位置基本一致, 符合边坡在大暴雨工况下发生失稳的实际情况。因此, 本文运用Geo-Studio有限元数值分析软件对滑坡进行数值模拟, 并基于此分析其稳定性是可靠的。

图14 边坡稳定系数与时间的关系

图15 54 h危险滑移面位置图
4 结 论
(1)降雨入渗过程中边坡的渗流场、 应力场、 位移场变化规律: 孔隙水压力与体积含水量受降雨入渗的影响在浅表层土体发生剧烈变化, 与降雨强度呈正相关关系, 且降雨停止后的一段时间内仍能保持, 表现出一定的滞后性; 边坡表面土体最大剪应力增大, 坡脚处剪应力集中区范围扩大; 水平、 竖向位移在降雨作用下均呈逐渐增加的态势, 浅层土体位移变化幅度较大, 坡顶处竖向位移最大, 坡脚处水平位移为主。
(2)实际中, 大多数的边坡处于非饱和状态, 降雨入渗过程本质是边坡从上到下由非饱和状态转变为局部饱和状态的渐变过程, 对于非饱和区, 体积含水量的增加造成基质吸力、 有效应力下降, 弱化土体抗剪强度, 对边坡的稳定性产生不利影响。
(3)采用有限元极限平衡法研究降雨作用下边坡的稳定性, 稳定系数随着降雨持时的增大而减小, 最小稳定系数出现在雨停后一段时间, 计算所得滑移面位置和实际情况接近, 说明本文采用Geo-Studio有限元数值分析软件对滑坡进行数值模拟研究结论可靠, 可为非饱和土边坡的变形与稳定分析提供一定的参考与借鉴。
