简化线热源对ATRT计算土体导热系数的影响——数值模拟研究

刘 浩,顾 凯,张 博,魏 壮,罗 淇,施 斌,苏晶文

(1.南京大学地球科学与工程学院,江苏 南京 210023;2.中国地质调查局南京地质调查中心,江苏 南京 210016)

地热能是一种全天候的零排放可再生能源,受到了研究者的广泛关注[1-4]。浅层地热能的开发对我国非传统冬季采暖区供暖意义重大[5-6]。地源热泵是利用浅层地热能的主要方式[7],通过流体在钻孔换热器(Borehole Heat Exchanger, BHE)内的循环实现热量交换,使得地表建筑物可以达到“冬暖夏凉”效果。导热系数作为表征土体热量传递的重要热物理参数,直接影响地源热泵系统的设计成本。

热响应测试(Thermal Response Test, TRT)是原位评估土体导热系数的主要方法(图1)。一定温度的流体从换热管进口端注入,在管内循环的同时向四周土体散热,并记录换热管出口流体的温度,根据线热源理论计算得到周围土体的导热系数。这种方法通常获得地层的平均导热系数,不能获得导热系数随深度的变化[7]。为了获取不同地层的导热系数,学者们在TRT的基础上提出了基于分布式测温技术(Distributed Temperature Sensing, DTS)的分布式热响应测试方法(Distributed Thermal Response Test, DTRT)(图1)[8-9]。然而,以循环水为热源的TRT和DTRT测试时间相对较长(现行规范推荐测试时间不少于48 h[10])、成本较高。为了提高测试效率,有学者提出以加热电阻为热源的热响应测试方法,如主动加热光纤热响应测试(Actively Heated Fiber Optics Based Thermal Response Test, ATRT)[11]。ATRT利用铜网内加热光缆代替循环流体进行加热,内加热光缆中铜网为热源,通电后产生热量,被铜网包裹的光纤为测温传感器,线热源和测温传感器高度集成在一起。现场试验结果表明,ATRT可以有效降低导热系数测试成本,提高测试效率[11]。

图1 TRT和DTRT示意图Fig. 1 Schematic for the TRT and DTRT

目前,在ATRT以及其它复合光缆热响应测试中,加热光缆的布设方式主要有两种:一是将内加热光缆通过轧带或胶带与换热管固定在一起[11-13](图2(a)),另一种是将内加热光缆布设在硬管两侧[14](图2(b))。目前,作者所在研究团队在江苏常州热响应试验场地实施了图2(c)、图2(d)方式的热响应测试。在计算土体导热系数时均需要将不同布设方式的内加热光缆简化为线热源[10],不同布设方式对热响应测试的影响主要体现在内加热光缆间距的差异。大量研究已经证明了在TRT和DTRT中将BHE简化为线热源进行导热系数计算的可行性[15-18],但由于内加热光缆半径远小于换热管,其在钻孔内的状态相对于钻孔本身来说存在不确定性,简单地采用TRT研究中将整个钻孔作为线热源的方法可能会对导热系数计算造成较大的误差,因此,ATRT作为一种新型的热响应试验方法,如何将钻孔中U型布设的内加热光缆简化为线热源需要进一步量化研究。

图2 基于主动加热光缆的热响应测试中光缆布设方式示意图Fig. 2 Schematic diagram for different test setups for the actively heated fiber optics based thermal response test

数值模拟方法是地热能研究中广泛使用的有效方法[19],通过数值方法进行热响应测试模拟,具有精度不受限制、不同位置温度获取成本低以及试验条件可以快速改变等诸多优势。LUO J等[20]利用数值模拟方法探究了地下水对换热管换热性能的影响;WAGNER V等[16]利用数值方法研究了U型换热管间距、不均匀初始温度分布和地下水引起的热弥散等因素对TRT结果的影响;ARANZABA N等[21]利用数值方法模拟不同条件下TRT,结果与现场试验数据具有很高的一致性。数值模拟方法在热响应测试研究的有效应用,为现场试验提供了有益的参考。

本文利用有限元数值模拟软件ComsolMultiphysics构建二维多孔介质传热模型,基于常见的热响应测试钻孔结构,建立不同内加热光缆间距模型和理想线热源模型,通过分析热响应测试中温度变化规律以及对比导热系数计算结果差异,探究简化线热源进行导热系数计算的可行性以及内加热光缆间距对测试结果的影响。

1 理论与方法

1.1 线热源理论

INGERSOLL L R[22]最早用线热源理论来解决地埋管换热器中的传热问题,将BHE简化成一个具有恒定加热功率的无限长线热源,而周围地层的传热过程简化为一维轴对称瞬态热传导问题进行计算,即相当于在均匀、各向同性的无限介质中有一根长径比非常大的热源(假设为一根线),忽略垂向的传热,忽略热源与待测介质间的接触热阻,周围土体的温度时空变化由以下方程描述。

(1)

式中:T(r,t)是周围土体距离热源中心r位置处t时刻的温度,℃;T0是土体初始温度,℃;q是线热源单位长度的加热功率,W/m;λ是土体的导热系数,W·m-1·K-1;α是土体的热扩散系数,m2·s-1。

如果加热时间足够长,则在土体中任意一点的温升与时间的对数之间近似线性关系,斜率与土体的导热系数有关,公式(1)简化为

ΔT=T-T0≈klnt+C,

(2)

(3)

式中:ΔT是温升,℃;k是T-lnt关系曲线的斜率;C为常数。

根据公式(3),计算得到的导热系数为

(4)

基于公式(4),即可根据热源处的温升随对数时间变化曲线的斜率dT/(dlnt)计算得到周围土体的导热系数。

1.2 数值模型

利用ComsolMultiphsics数值模拟软件建立二维数值模型,选用多孔介质传热物理场,满足公式(5)、公式(6)。需要指出的是,基于线热源的计算通常忽略不同深度上未稳定的温度差异引起的垂向传热过程,故二维数值模型可以满足研究需要,并具有较高的计算效率(图3)。基于热响应试验钻孔常见的结构,构建的数值模型主要由钻孔和待测土体组成,钻孔包括回填料和内加热光缆。数值模型直径2 000 mm,钻孔直径120 mm,内加热光缆简化为加热电阻和光缆护套两部分,加热电阻直径为4 mm,光缆护套厚度为1 mm。

(a)双热源模型用以模拟实际中的U型内加热光缆; (b)单热源模型用以模拟理想的线热源图3 数值模型示意图Fig. 3 Schematic diagram for the numerical model

为了探讨内加热光缆间距对热响应测试的影响,设置了两类光缆布设方式:①用中心对称位置的两个热源模拟U型内加热光缆(图3(a));为了研究加热光缆不同间距对计算结果的影响,在数值模型中设置U型布设内加热光缆中心间距分别为6 mm(光缆并在一起)、10 mm、20 mm、30 mm、40 mm、50 mm、60 mm、70 mm、80 mm的9个双热源模型(图4);②模型中心只有一个热源,用于模拟理想线热源(图3(b))。

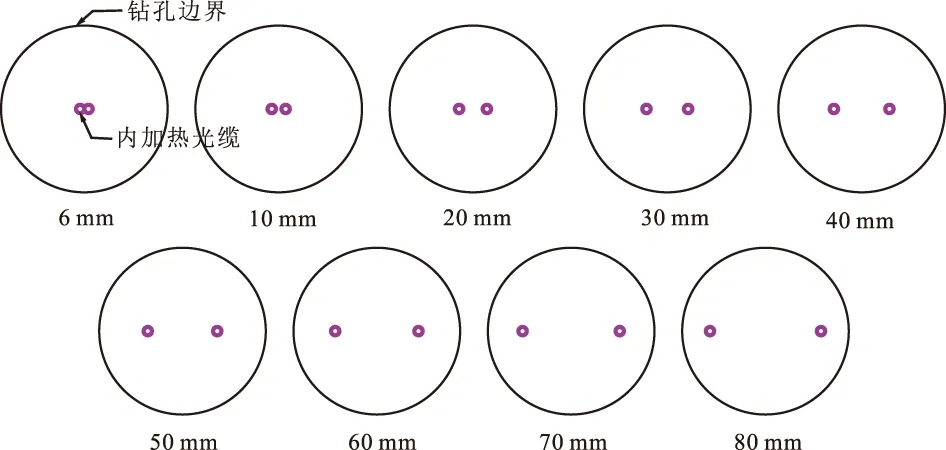
图4 不同间距的U型光缆位置示意图Fig. 4 Schematic diagram for the position of U-shaped optical cables with different spacing

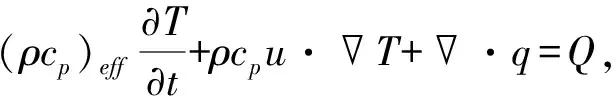
(5)

q=-keffT,

(6)

式中:T是多孔介质(包括固体和流体)的平均温度,K;ρ是流体密度,kg·m-3;cp是恒压下的流体热容,J·kg-1·K-1;(ρcp)eff是恒压下的有效体积热容;Keff是有效导热系数,W·m-1·K-1;u是流体流速,m·s-1;Q是热源单位体积的加热功率,W·m-3。当流速u为0时,公式(5)就简化为热传导问题。

数值模型各部分材料参数根据实际材料的典型值进行取值(表1),其中回填料采用饱和石英砂的热物性参数。假设内加热光缆、回填料和周围土体之间热量已平衡,初始温度一致,设置为20 ℃。为了保证向钻孔和土体内注入的总热量一致,U型内加热光缆中单个热源的加热功率为10 W/m,而理想线热源加热功率为20 W/m,加热持续时间均为30 000 s。在双热源模型中由于两个热源中心对称,温升相同,所以选择其中一根热源中心的温升数据作为测试结果,符合实际实验中由光缆中心的光纤测温的形式。

表1 材料参数表

2 结果与讨论

2.1 热响应测试过程

不同内加热光缆间距的双热源模型和理想线热源模型中实施的热响应测试结果如图5所示。热响应曲线与公式(1)、(2)描述的规律一致,随着加热时间的延长,温升与时间的对数逐渐趋于线性关系,即温升速率在早期较大,随着时间增加,温升速率逐渐降低。进一步的,选取理想线热源模型和内加热光缆间距80 mm模型中热响应测试过程曲线如图6所示。通过改变回填料的导热系数(λg)和土体的导热系数(λs),在两类模型中分别实施三组热响应测试。图6(a)为理想线热源条件下不同热响应测试的结果,图中实线为三个数值模型温升和时间对数之间的关系曲线,虚线为温升随时间对数变化的曲线斜率和时间对数的关系曲线。根据虚线间的相互关系,可以将热响应过程分为3个阶段:阶段Ⅰ是内加热光缆影响阶段,范围为开始加热到斜率曲线第一次相互分开(大约10 s时),该阶段由于主要受到内加热光缆护套的低导热系数的影响使得温升在时间对数上的导数快速增大至接近峰值,各曲线相互重合,说明还未受到回填料和土体的影响;阶段Ⅱ是回填料影响阶段,范围为阶段Ⅰ结束到斜率曲线第二次相互分开(大约1 100 s),该阶段由于所设置的回填料的导热系数不同而使得曲线相互分开,回填料导热系数低的数值模型温升随时间对数的导数相对较大,但总体保持着相似的曲线变化形式,该阶段不同土体的模型的导数曲线还未分开,此时还未受到土体的影响;阶段Ⅲ是土体影响阶段,范围是Ⅱ阶段结束到加热终止,该阶段斜率曲线(λg=2.6 W·m-1·K-1,λs=2.0 W·m-1·K-1)逐渐上升接近斜率曲线(λg=2.0 W·m-1·K-1,λs=2.0 W·m-1·K-1),体现土体对热响应测试过程逐渐起主导作用。

图5 不同数值模型得到的热响应曲线Fig. 5 Thermal response curves obtained from different numerical models

(a).理想线热源模型;(b).双热源模型(内加热光缆间距80 mm)图6 热响应测试过程Fig. 6 Illustration of thermal response test process

从内加热光缆间距80 mm模型中实施的三次热响应测试结果(图6(b))来看,热响应测试过程同样可以和理想线热源模型一样分成3个阶段。不同的是其温升在时间对数下的导数值明显低于理想线热源模型的导数值,且Ⅱ阶段的结束位置要早于线性模型(大约400 s),体现热源向土体传热效率的提高,但是U型的布设方式使得土体和回填料导热系数一致的模型的斜率曲线在Ⅲ阶段也在不断上升,需要较长的时间达到稳定值,反映测试效率的降低。

基于建立的数值模型,对比了理想线热源模型和所有间距的U型布设内加热光缆模型下热响应测试过程分析曲线(图7)。对比内加热光缆间距80 mm的模型和理想线热源模型所得到的斜率曲线可知,在加热开始的阶段(<400 s)理想线热源模型中温升随时间对数的导数大致为内加热光缆间距80 mm模型的两倍,这是因为在加热开始阶段内受到低导热系数护套的影响,热量在光缆内积蓄,需要一段时间使得光缆升到一定的温度向外稳定传热,之后可以将光缆看作一根线热源,在加热前期U型布设的内加热光缆之间还没有显著的相互影响,都近似于一根加热功率为10 W/m的线热源单独与周围回填料以及土体作用,而理想线热源模型中加热功率为20 W/m,由于温升随对数时间变化的曲线斜率与加热功率q成正比,所以理想线热源模型得到的温升斜率大致为内加热光缆U型布设模型的两倍。随着加热时间的延长,U型布设的内加热光缆之间相互影响,其对应温升斜率逐渐接近于理想线热源模型。

缩减内加热光缆的间距,内加热光缆之间的热量传递距离变短,会在更短的加热时间内开始相互影响。因此在相同时间内加热光缆位置积聚的热量越多,表现在相同的加热时间下,内加热光缆间距越小,温升值越高。图7中可以看到随着内加热光缆间距的缩小,其温升斜率曲线越快地偏离内加热光缆间距80 mm模型的斜率曲线,并趋近理想线热源模型的结果。

图7 热响应测试过程温升曲线对比(U型布设内加热光缆模型和理想线热源模型)Fig. 7 Comparison of the temperature rise curves during hydrothermal response testing (U-shaped optical cable model internally heated vs. ideal line heat source model)

2.2 导热系数计算误差

基于2.1节中对不同间距内加热光缆条件下的热响应测试过程分析,简化U型布设的内加热光缆为线热源,将温升斜率值带入方程式(4)计算得到导热系数值随时间变化的结果如图8所示。U型布设的内加热光缆在加热初期近似于两根单独的线热源,温升反映单个热源所测得的回填料以及土体的真实性质,由于计算时带入的加热功率是U型布设的内加热光缆的总功率,故而增大了导热系数计算值,导热系数-时间曲线在加热初期出现一个峰值。内加热光缆间距越大,U型布设模型中两个热源相互影响作用得越慢,峰值出现的越晚,峰值越大。在内加热光缆之间开始相互影响后,U型布设的内加热光缆逐渐等效成加热功率为两倍输入功率的理想线热源,导热系数从峰值开始下降。随着加热时间的增加,导热系数收敛于土体预设导热系数值,且随着内加热光缆间距的减小,收敛于土体预设导热系数的速度越快。当加热时间较长时(>26 000 s),无论是线热源模型还是各种间距双热源模型都能得到较高精度的测试结果(与土体预设导热系数值相比误差<10%)。

图8 导热系数随对数时间变化图Fig. 8 Calculated thermal conductivity over logarithmic time

不同内加热光缆间距条件下一定加热时间的导热系数计算结果如图9所示,当间距不断增大时,不同加热时间所计算得到的导热系数值均随之增大,导热系数的计算误差与内加热光缆间距呈正相关。在加热480 min时,内加热光缆间距对于导热系数计算结果的影响不再明显。导热系数计算误差等于10%对应的加热时间定义为建议加热时间,绘制内加热光缆间距对应的建议加热时间结果如图10所示。随着内加热光缆间距的增大,建议加热时间增加,且增加速率逐渐增大,反映出测试效率的加速降低。因此,在单根内加热光缆未出现的情况下,原位应用ATRT评价地层导热系数时应尽量减小内加热光缆的间距,内加热光缆并在一起的布设方式在理论上有着更高的测试效率。

图9 导热系数计算值随间距变化图(假设理想线热源模型间距为0 mm)Fig. 9 The calculated value of thermal conductivity under different heating time varies with spacing (Assuming that the spacing of the ideal line source is 0 mm)

图10 不同间距下的建议加热时间(假设理想线热源模型间距为0 mm)Fig. 10 Suggested heating time under different spacing (Assuming that the spacing of the ideal line source is 0 mm)

3 结论

将布设在钻孔中的内加热光缆简化为线热源是实施ATRT获取地层导热系数的重要前提,基于ComsolMultiphysics有限元数值模拟软件研究了U型光缆间距对热响应测试的影响。用于研究的双热源模型中光缆间距分别设为6 mm(光缆并在一起)、10 mm、20 mm、30 mm、40 mm、50 mm、60 mm、70 mm、80 mm,此外建立了理想线热源模型。在数值模型中实施热响应测试得到不同条件下温升曲线,通过不同条件下温升曲线以及导热系数计算结果的对比,得到了以下结论。

(1)根据加热后内加热光缆的温度变化,ATRT的加热过程可以分为3个阶段,分别是光缆影响阶段、回填料影响阶段和土体影响阶段。U型布设光缆会增加土体影响阶段达到稳定时的加热时间,不利于提高ATRT计算导热系数的效率。

(2)U型光缆在加热初期主要表现为两根线热源进行单独加热,光缆之间的相互影响可以忽略不计。两根线热源开始相互影响的时间长短和光缆间距呈正比,即光缆间距越大,在更长的加热时间下,两根内加热光缆之间才开始相互影响。导热系数在时间上表现为加热初期出现一个明显大于土体的导热系数峰值。

(3)随着加热时间的增加,U型光缆布设条件下温升速率逐渐接近理想线热源温升速率,U型光缆逐渐可以简化为线热源,计算所得的导热系数也逐渐收敛于土体预设导热系数。缩小内加热光缆间距,可以加速上述过程。

(4)在一定的加热时间条件下,缩小U型光缆间距可以降低导热系数计算的误差。内加热光缆间距的增大使得建议加热时间随之增加,且增加速率逐渐变大。在U型布设内加热光缆条件下,内加热光缆并在一起的方式具有最高的测试效率。