汉简《算数书》“少广术”求最小公倍数法

2021-08-20周序林张显成何均洪

西南民族大学学报（自然科学版） 2021年4期

周序林，张显成，何均洪

(1.西南民族大学中国语言文学学院，四川成都610041；2.西南大学汉语言文献研究所，重庆北碚400715；3.中国民用航空飞行学院大飞机学院，四川广汉618307)

1 问题的提出

《九章算术》有“少广”章.(唐)李籍认为:“广少，纵多，截纵之多，益广之少，故曰少广.”[1](唐)李淳风认为:“一亩之田，广一步，长二百四十步.今欲截取其纵少，以益其广，故曰少广.”[2]可见，“少广”指在田面积1亩不变的情况下，田宽在1步的基础上有少量增长时求田的长度.《九章算术》“少广”章有关例题的田宽可表示为步(n＝2，3，…，12).“少广”算题需要对田宽诸分数进行通分.《九章算术》“合分术”本有“母相乘”的通分方法[2].(唐)李淳风指出这种通分法的缺点是“列数尤多”“算数至繁”，因此特制少广术“从省约”[2].《九章算术》“少广术”求田宽诸分母公倍数的方法是:

置全步及分母子，以最下分母徧乘诸分子及全步，各以其母除其子，置之于左；命通分者，又以分母徧乘诸分子及已通者，皆通而同之.[2]

此法只要遵循“能除则除，能约则约”的原则，就能算得诸分母的最小公倍数.

出土汉简《算数书》简164―165也载有“少广术”[3]，我们依据竹简红外线图版将该术简文整理如下(简体行文，均用通用字，简文符号略):“投少广之术曰:先置广，即曰，下有若干步，以一为若干，以半为若干，以三分为若干，积分以尽所投分，同之以为法.即藉置田二百四十步，亦以一为若干以为积步，除，积步如法得纵一步，不盈步者，以法命其分.”

学界普遍认为，《算数书》“少广术”没有求最小公倍数的算法[4－8].我们认为，这是对《算数书》“少广术”的误解，造成这种误解的主要原因是对术文(尤其是“积分以尽所投分”)理解有误[3，5，9－12]和对《算数书》的文献性质认识不足.我们认为《算数书》“少广术”有求最小公倍数的算法，讲述这一算法的术文是:“先置广，即曰，下有若干步，以一为若干，以半为若干，以三分为若干，积分以尽所投分.”下文将对此算法进行分析.

2 《算数书》“少广术”新解

现将《算数书》和《九章算术》“少广术”求最小公倍数算法的术文分解并对比如表1，观察二者是否存在对应关系.

表1 《九章算术》与《算数书》“少广术”最小公倍数算法术文对比Table 1 Comparison between the methods for finding LCM in the Jiuzhang suanshu and the Suanshu shu

图1 设置田广Fig.1 Putting down the width of a field on the counting board

步骤2:以最下分母为例演示如何化分数为整数，分以下三个步骤进行.

其中，步骤2(a)中“最下分母”指位于筹算板最下面的那个分母n，“以最下分母徧乘诸分子及全步”指用n分别乘以田广步中的全步1和每一个分数的分子，如图2右列.简文“下有若干步”指位于筹算板最下面的步数(即步)；简文“以一为若干，以半为若干，以三分为若干”中的“一”“半”“三分”为不完全例举，其后还有若干个分数，直至；古算表达方式“以a为若干”指“某数乘以a得若干”；整句简文指用n分别乘以田广步中每一个数，如图2右列.显然，《九章算术》相较《算数书》而言，表达方式更加概括、抽象.

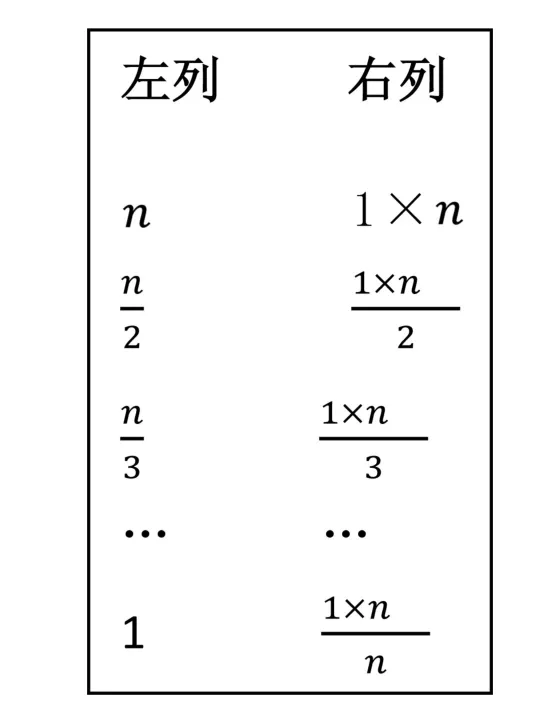
图2 最下分母n乘全步及诸分子Fig.2 Multiplying the width by the denominator at the bottom of the counting board

步骤2(b)中“各以其母除其子”指步骤2(a)中最下分母n与田广诸分子的乘积除以各自的分母(如图2左列)，即:只要贯彻“能除则除”“能约则约”的原则，就可以确保最终算得最小公倍数.《算数书》没有表达“能除则除”“能约则约”的术文.《算数书》在“少广术”后面有9个“少广”例题[9]，演算这些例题时发现，图2右列的运算中存在“可除”“可约”的可能，现将其次数、分布状况和所得公倍数统计如表2.

表2 《算数书》“少广”例题中“可除”“可约”次数及所得公倍数Table 2 The number of times of dividing and fraction－simplifying when finding LCM in the 9 Shaoguang problems in the Suanshu shu

这9个例题共有45次“可除”和7次“可约”，各例题所得公倍数均为最小公倍数.可见，《算数书》“少广”算题在分母乘全步和诸分子的过程中，都遵循了“可除则除”“可约则约”的原则，从而算得了诸分母的最小公倍数.此外，《算数书》还将“少广术”求最小公倍数法应用于非“少广”类算题，如“径分”“石率”“贾盐”“米出钱”算题[9]，这时同样严格遵循了“可除则除”“可约则约”的原则.相反，《九章算术》没有严格遵循这一原则，例如，1＋＝6，12)的最小公倍数应该分别是60和27，720，但《九章算术》“少广”第5和第11例题分别算得120和83，160[2].为什么这两个例题没有遵循此原则尚待进一步研究.

步骤2(c)“置之于左”指把步骤2(a)、2(b)所得之数设置在左侧，如图2左列.《算数书》无此表达，但不影响计算结果.

步骤3:如何把其余分数化为整数.《九章算术》术文“命通分者，又以分母徧乘诸分子及已通者，皆通而同之”讲述如何把其余分数转化为整数，方法是:逐次以分母乘整数和各分子，直至所有分数化为整数为止[13].我们认为，《算数书》术文“积分以尽所投分”讲述了相同方法.理解这条术文的关键是“积分”的含义.刘徽在《九章算术·方田》“径分术”中讲如何将带分数化为假分数时论及“分母乘全……散全则为积分[2]”，白尚恕(1983)认为刘徽称“分母乘全”为“积分”[13].“积分”指带分数的分母乘以带分数的整数，可引申指由这种乘法运算所得的乘积.就“少广术”田广(1＋中分数构成的特殊性而言，“分母”在“乘全”的同时还需要乘诸分数，因此《算数书》“少广术”中的“积分”指分母乘以整数以及诸分子.可见，《算数书》术文“积分”与《九章算术》术文“又以分母徧乘诸分子及已通者”含义相同.此外，《算数书》术文“尽”意为“化尽”，“投”意为“计算”，“所投分”指所需要计算的分数，即田广(1＋ 12步中的).因此“以尽所投分”意为:以把中所有分数化为整数，这与《九章算术》术文“皆通而同之”表达的意思相同.

综上，《算数书》“少广术”术文“先置广，即曰，下有若干步，以一为若干，以半为若干，以三分为若干，积分以尽所投分”除两处省略外(见表1)，其余均与《九章算术》“少广术”相关术文呈对应关系，其内容可概括为:在筹算板上设置田广)步，然后以最下分母n为例演示如何把分数转化为整数，最后讲述如何化其余分数为整数.术文省略但严格遵循了“可除则除”“可约则约”的原则.

3 “可除则除”“可约则约”原则省略的原因

“少广术”只要坚持“可除则除”“可约则约”的原则，就可以求得最小公倍数.《算数书》严格地遵循了这一原则，但为什么这一原则在术文中没有出现呢?这与《算数书》的文献性质有关.邹大海(2001)认为《算数书》的性质是一本“不大成系统的撮编之书”[4].因此《算数书》的语言表达还不够规范统一，常有省略与简省，其情形有三.第一是上文出现过的简文，如果在相同语境中再次出现，则往往省略.如“狐皮”算题简36―37“狐出十二七十二分十一，狸出八〔七十二〕分卌九，犬出四〔七十二〕分十二”[10]，其中〔七十二〕就是承上省略的简文.第二是程序化的表达法往往采用简省形式，如《算数书》描述做除法的程序，完整的表达如“妇织”算题简56“……以为法，……以为实，如法而一尺，不盈尺者，以法命分”[10]，往往简省为如“传马”算题简53“以……为法，以……为实”[10]，甚至简省为如“程竹”算题简70、71“以……为法”[10]，因为在古人看来，只要看到“以为法”就知道需要做除法运算了，故采用简省的表达而不需费尽笔墨完整地表达整个程序.《算数书》中这种简省的形式，正如邹大海(2001)所言:“一些简省的表述说明《算数书》是在罗列一些已有的方法、算题或利用已有的方法解决应用问题:换句话说，《算数书》中这些部分的方法是早已有之的.”[4]三是常识性知识的省略，如圆周率取值为3和“方五斜七”，这些知识在古人看来是常识，因此在《算数书》中没有必要交代，而是直接运用.这类省略对于现代的读者来说比较隐晦，需要从算题的数据中寻找蛛丝马迹.

根据以上三种省略，结合前文对“少广术”的分析，我们可以得出三个结论.一是“少广”例题都承术文省略了最小公倍数的计算过程而直接使用最小公倍数进行通分.如例题((n＝4)省略了计算最小公倍数12的过程，而直接使用最小公倍数12进行通分.二是“少广术”是“早已有之”的算法.不仅如此，它还为人们熟悉并广泛运用(见上文).正因为“少广术”是“早已有之”、为人熟悉并广泛运用的算法，它才能以简省的形式出现(即省略“可除则除”“可约则约”).三是所省略的“可除则除”“可约则约”是常识性知识，以至于在用“少广术”求最小公倍数的计算过程中，不需要明言这一原则，古人都会一贯地、严格地执行.