I/Q不平衡的分析与补偿的研究

余骁禹

(西南民族大学计算机科学与工程学院，四川 成都610041)

1 绪论

通信系统中，在这个电子信息系统使用越发频繁的年代，屡见不鲜.在通信系统中大量使用的数字射频芯片，几乎都是利用了I/Q信号.I/Q信号，是电子电路中最常见的射频信号[1]，其中I(In－phase)表示同相，Q(Quadrature)表示正交，既与I信号相位差90°.

从模拟信号时代进入数字信号时代以后，单一信号或信号组集合，在某一时间点只有一个信号频率.这使得使用数字域进行I/Q两路正交调制和正交解调的I/Q系统使用更加频发.然而，在实际的通信系统中，由于模块设计，器件选取，电路布局等各种误差[2]，都会造成I/Q信道的不平衡.

理想的I/Q信号，为只有相位正交，幅度和其他属性均相等的两列信号.但由于本振信号的误差，本振泄露，输入信号本身的误差等原因，往往会导致幅度不相等，相位不正交，直流分量干扰[3].

本文将这些干扰源，转换为数学模型，结合矩阵模型[4]，先进行时域上的信号矫正并仿真，并不断调整模型参数，达到合理的模型后，进行实测数据的验证，并将得到的数据进行频域转换，并进行傅里叶变换，根据结果验证和修正模型.

2 数学模型

2.1 基础模型

图1，是一路信号转成两路I/Q信号的基础模型[5].其中图2是零差式结构产生I/Q信号的由本振产生的过程[6].从图中我们不难看出，I/Q信号的产生，是在I/Q调制(Modulation)或I/Q解调(demodulator)的过程[7]，在信号划分时，是通过一路信号y(t)经过本地振荡器(Local Oscillator)经过相乘运算，从而得到I(t)，Q(t)两路信号，由于这里采用零差式结构，共享一个本振，而该本振本身产生两路正交的信号，这使得本振产生的两路信号和y(t)信号混合时，就出现了两路信号I(t)和Q(t).

图1 基础模型Fig.1 Base Model

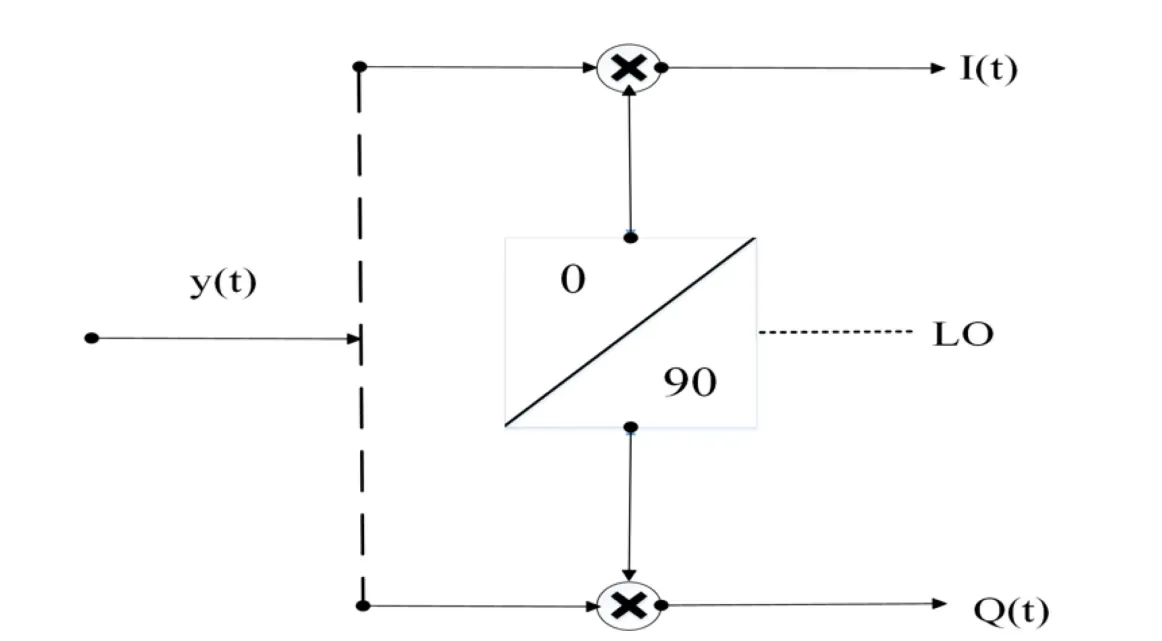
图2 I/Q信号产生过程Fig.2 I/Q Signal Generation Process

在理想情况下，只要能使得本振[8]能产生两路幅度相等的正交信号，那经过本振后产生的两路信号，也会是理想的幅度相同，相位正交的两路信号，可得到标准信号公式

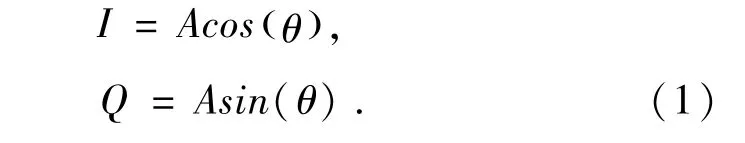
其中I，Q分别为混合后产生的I信号和Q信号，A为增益幅度.由于这里的I信号和Q信号，为标准正交信号，这里使用cosθ()和s i n(θ)来表示.

2.2 误差模型

在实际做信号处理的时候，往往不可能直接使用公式(1)，因为误差的存在，会导致I/Q不平衡的产生.在产生I/Q信号的过程中，这种I/Q不平衡主要表现在幅度不平衡，相位不平衡，以及直流分量的产生.

幅度不平衡即为I/Q两路信号的幅度值不相等，也称增益不平衡，相位不平衡即为I/Q两路信号的相位差，不为90°.这两者主要是在系统在正交过程中上下变频的时候产生的[9]，属于不可避免的误差.

而直流分量的产生主要是由于直流信号的注入产生了偏磁现象[10]，也就是直流信号的注入对附近信号的影响所产生的，属于不可避免的误差.

将标准信号公式(1)叠加上误差，可以得到修正公式(2):

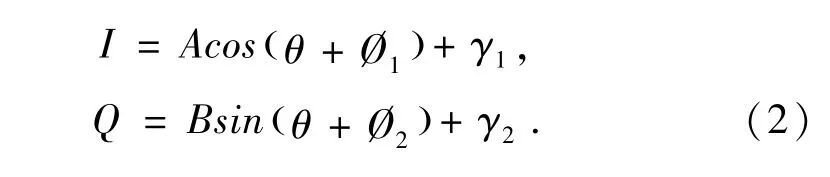
其中I，Q分别为混合后产生的I信号和Q信号，A为I信号产生增益幅度，B为Q信号产生的增益幅度；Ø1为I信号产生的相位偏移，Ø2未Q信号产生的相位偏移；γ1为I信号产生的直流偏量，γ2为Q信号产生的直流偏量.

由于我们的理想输出(矫正后的输出)信号依然满足公式1，所以理想输出信号I′，Q′与实际输出信号I，Q之间，必然存在着线性关系，即公式(3):

其中S为理想输出信号I'，Q'矩阵和实际输出信I，Q与直流偏量差值的矩阵的关系矩阵.

在该模型中，由于采用了标准正余弦信号，在采样点足够多的情况下，直流偏量，可以简化成均值，即为公式(4):

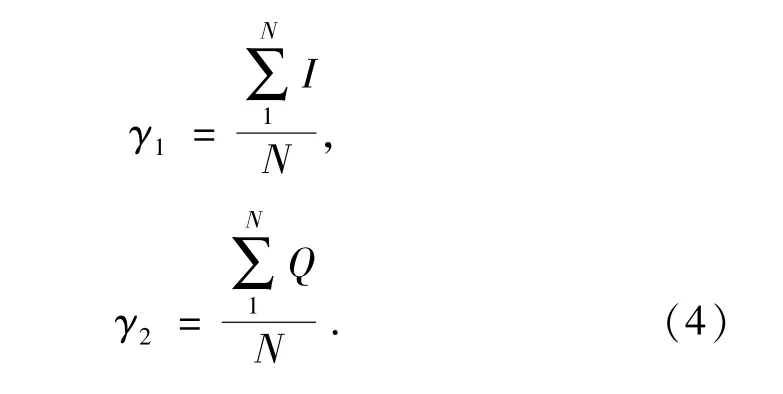
这样，就把误差模型变成了求解关系矩阵S，换言之，只要求出了关系矩阵S的数学模型，即可知道I/Q信号的补偿量.

2.3 简化模型

由于理想输出信号I'，Q'与实际输出I，Q，四个信号都为独立的一维矩阵，不难知道，关系矩阵S可用2X2的矩阵表示.即为公式(5):

针对这样的矩阵，求解困难，但可以利用I'，Q'之间的隐藏关系，幅度相等且正交，将I与Q两路独立的信号，转换为相关信号求解，即将某一路信号的误差，叠加在另一路信号上，如图3是叠加系统图，图4是叠加模型图[11]:

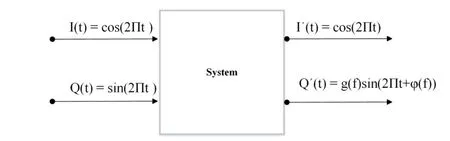
图3 叠加系统图Fig.3 Overlay System Diagram

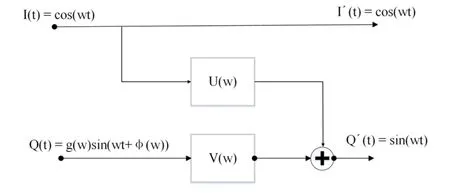
图4 叠加模型图Fig.4 Overlay Model Diagram

通过误差转移，我们将得到新的替换公式(6):

该替换公式以I为基准信号，将误差叠加在Q上，反之亦可.

将上式带回公式(3)，可得如下推导，公式(7)

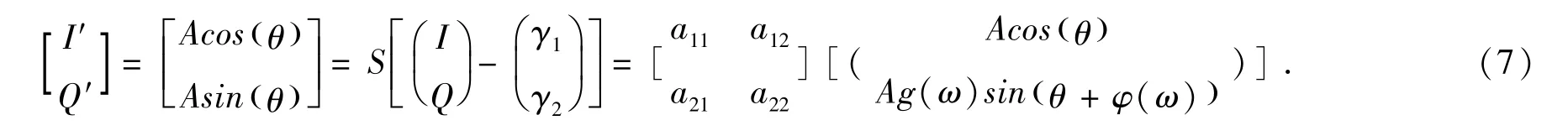
有三角函数特性可得公式(8):

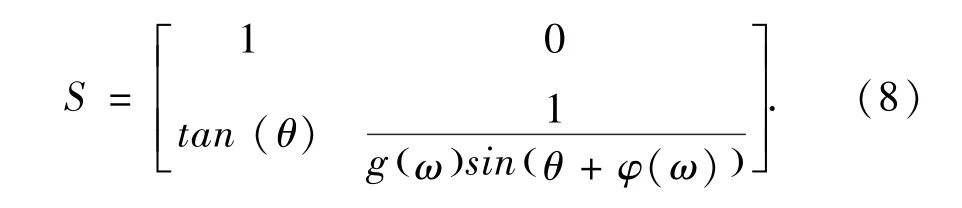
即得到了用相位误差和幅度误差表示的相关矩阵S.

2.4 指数模型

由于理想输出I′，Q′幅度相等，且正交，即可利用其指数特性，如公式(9):

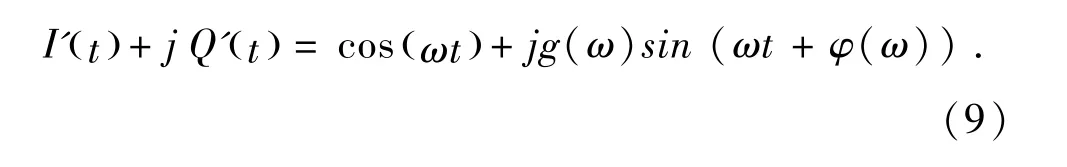
利用指数函数的特性公式(10):

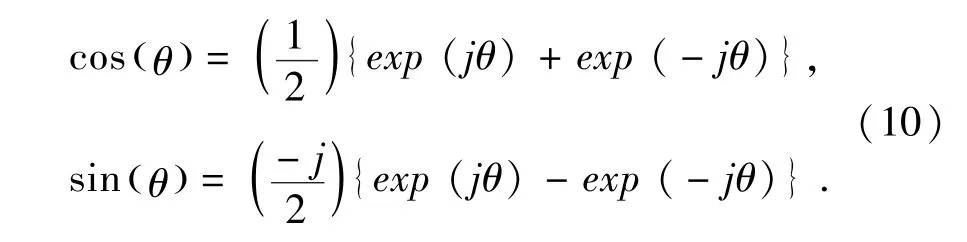
可将公式(9)替换为公式(11):

这样，就将公式转换成了实部和虚部.利用特性当A Toneω{ }无限趋近于1且A IMAGEω{ }无限趋近于0时，有gω( )无限趋近于1且φω( )无限趋近于0.

而在频域中，最大的误差镜像，可用一种常规的镜像抑制表示[12]，公式(12):

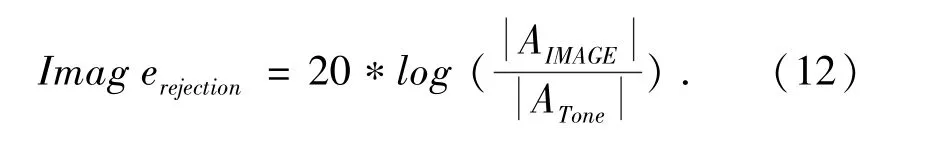
针对单频系统，可以使用特定值ω0来进行传统的不均衡补偿发，更新图4模型，图5是特定值简化模型.

图5 特定值简化模型Fig.5 Simplified Model Based on Specific Value

结合频域特性，可计算出ω0处的α，β，公式(13):

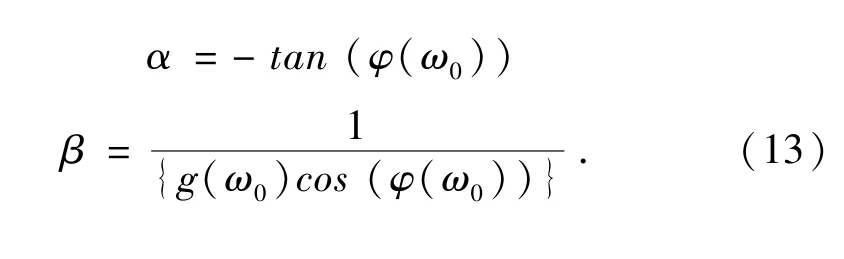
3 实验验证

3.1 基础模型时域仿真

在进行实测数据矫正之前，先对采用的模型，进行基础的时域模型[13]观测，这里对基础模型中的所有参量，A，γ1，γ2，gω( )，φ(ω)都进行随机值处理，选取一个周期[0～2π]，两百个基本点作为信号源进行数据仿真.可得到如下结果，如图6，7，基础模型时域仿真.

图6 I信号基础模型时域仿真Fig.6 Time Domain Simulation of Base Model for Signal I

图7 Q信号基础模型时域防针Fig.7 Time Domain Simulation of Base Model for Signal Q

该仿真采用I信号为基准信号，将误差叠加到Q路信号.

从仿真结果不难看出，I路信号的矫正结果，基本和理想输出重叠，这是因为采用I信号为基准信号，但Q信号只在实际输出信号上，有略微的矫正，效果较差.

3.2 修正模型时域仿真

重复试验后，发现依旧有这样的结果，经过反复测试，以及与实际数据的对比，发现Q信号矫正能力较弱的主要原因，在于误差信号的随机值选取，并未限定范围，而实际的误差偏差值，远远小于基础模型中产生的随机值，甚至在随机基础模型中，可能存在幅度波动大于本身幅度值的情况，所以根据出现了Q信号矫正能力较弱的现象.

针对该现象，对模型进行修正，根据实测数据和经验值，对基础模型的系数进行如下限定.

幅度A:[0.8～1.2]，γ1，γ2:[0.1～0.2]，gω( ):[0.9～1.1]，φ(ω):[－2.5～2.5].

进行误差范围限定修正后，再次进行数据仿真，可得到如下结果，如图8，9，修正模型时域仿真.

图8 I信号修正模型时域仿真Fig.8 Time Domain Simulation of Revised Model for Signal I

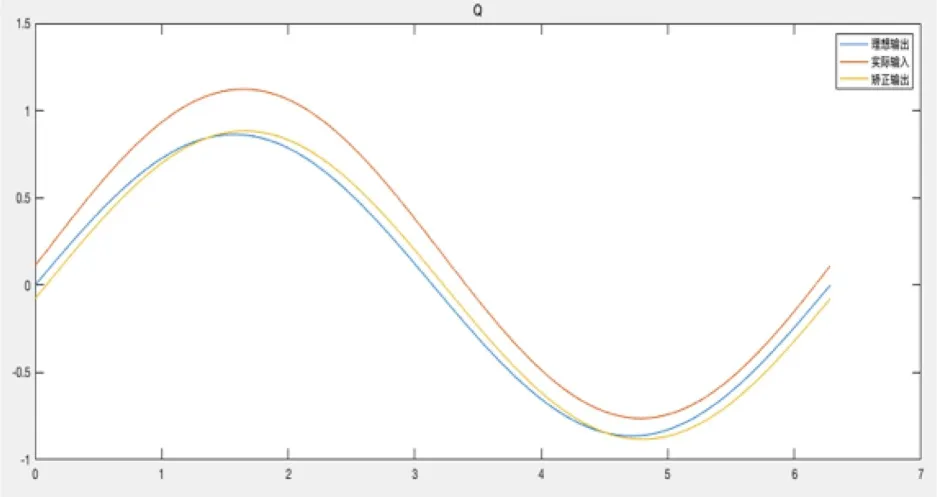
图9 Q信号修正模型时域仿真Fig.9 Time Domain Simulation of Revised Model for Signal Q

该仿真采用I信号为基准信号，将误差叠加到Q路信号.

从仿真结果可以看出，I信号的矫正结果，基本和理想输出重叠，Q信号的输出信号已在实际输出信号上有了极大的矫正，贴近理想输出信号.

通过修正模型的时域仿真，可以证明在时域情况，该补偿方法修正能力较强.

3.3 实测数据频域仿真

时域模型验证了该补偿方法可行后，下一步需要进行基于实测数据的测量，这里选用了频率从1010MHz到1500MHz，各50组I，Q信号，共计100路信号，其中每一路信号采样10240个点.部分实测数据如下表:表1，表2.

表1 I路信号实测数据样例表Table 1 Sample of Actual Data for Signal I

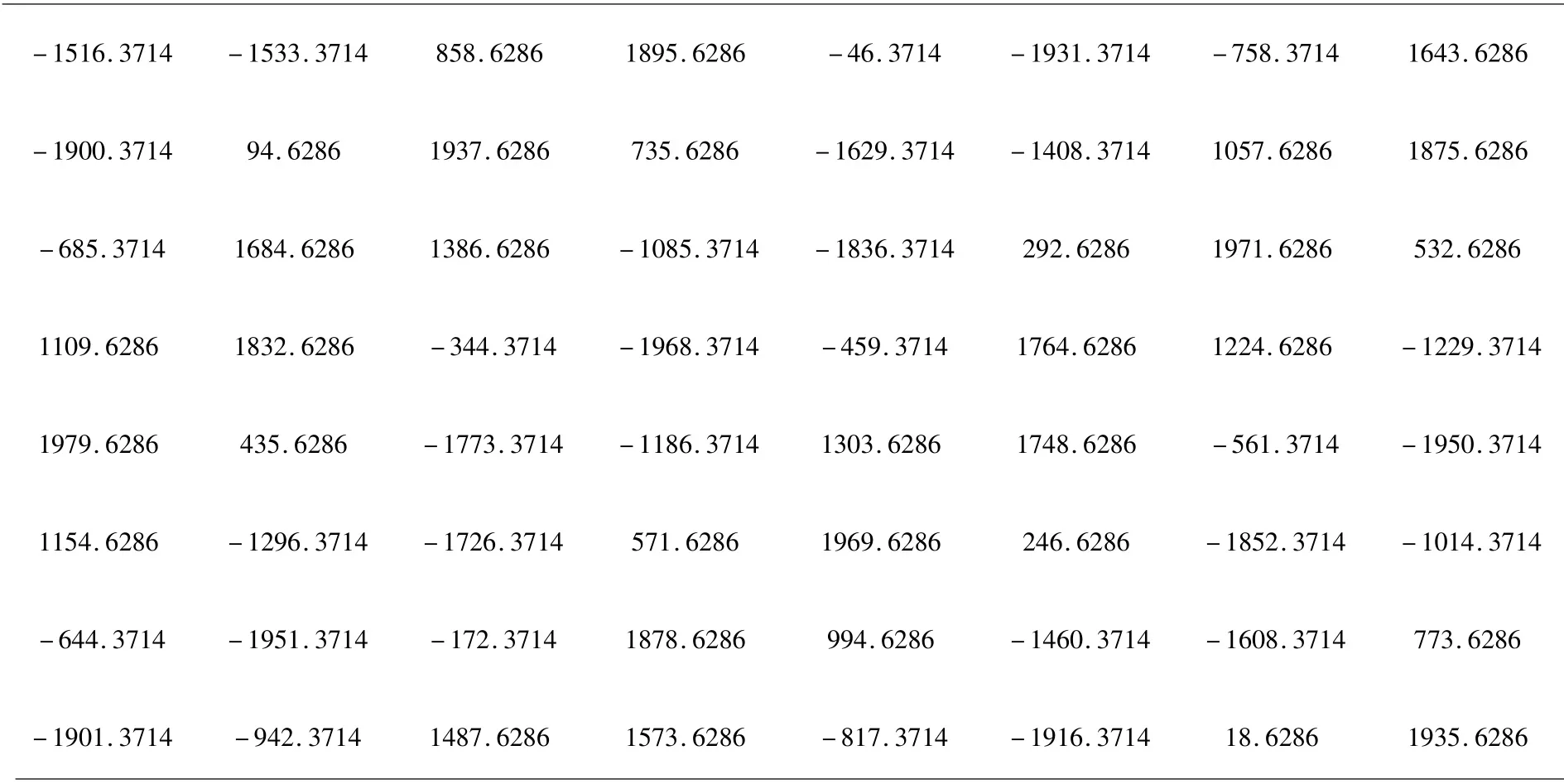
表2 Q路信号实测数据样例表Table 2 Sample of Actual Data for Signal Q

该表显示的为采样率为1190MHz的随机64个点的I路信号与Q路信号的采样结果，该表的数据沿纵向排列.

根据实测数据，进行时域仿真如下，如图10，11，实测数据时域仿真.

图10 原始输入信号实测数据时域仿真Fig.10 Time Domain Simulation of Actual Data for Original Signal

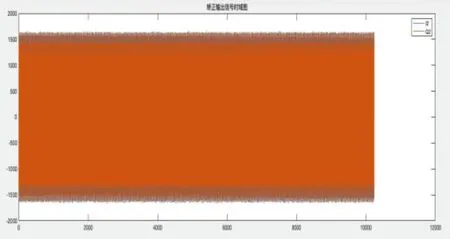
图11 矫正输出信号实测数据时域仿真Fig.11 Time Domain Simulation of Actual Data for Revised Signal

在图中我们很难观测到数据是否矫正，这是因为每组数据的采样点高达10240个，如此庞大的采样点叠加在时域信号中，导致结果不明，针对庞大的采样点，将采样结果进行傅里叶变换，进行频域显示，如图12，13所示，实测数据频域仿真.

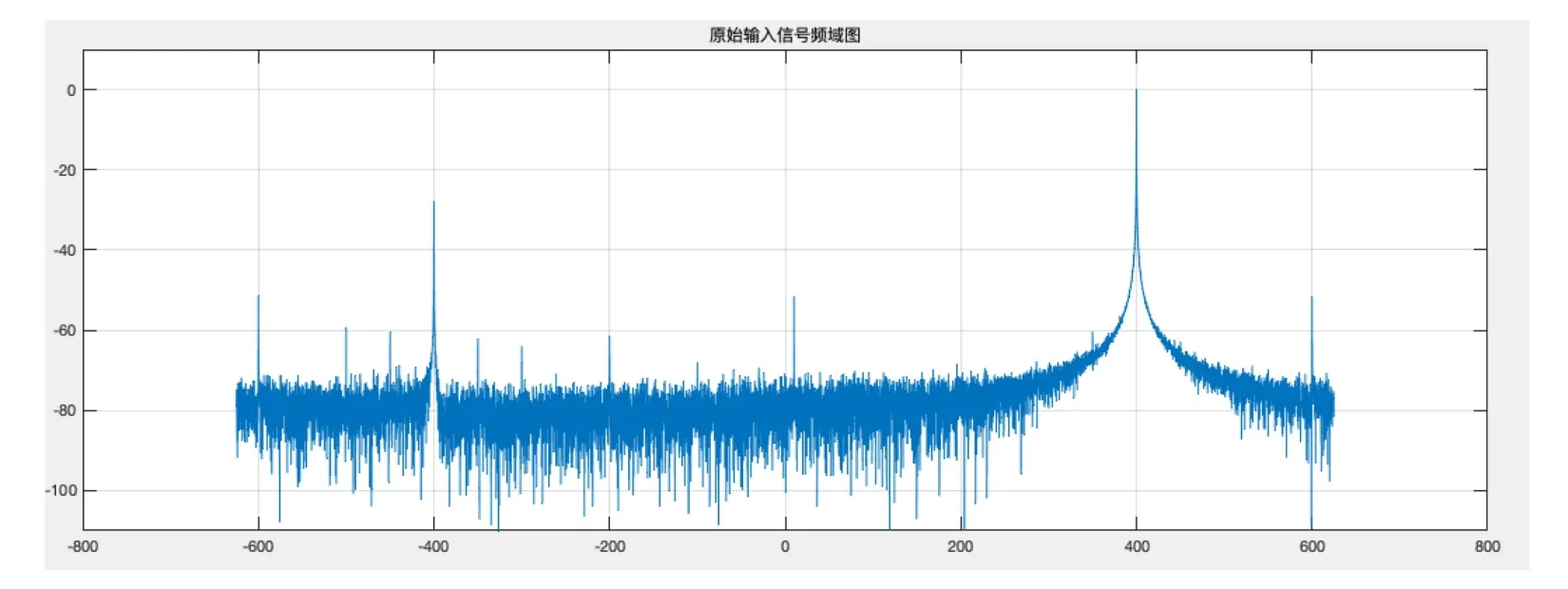
图12 原始信号频域仿真Fig.12 Frequency Domain Simulation of Actual Data for Original Signal

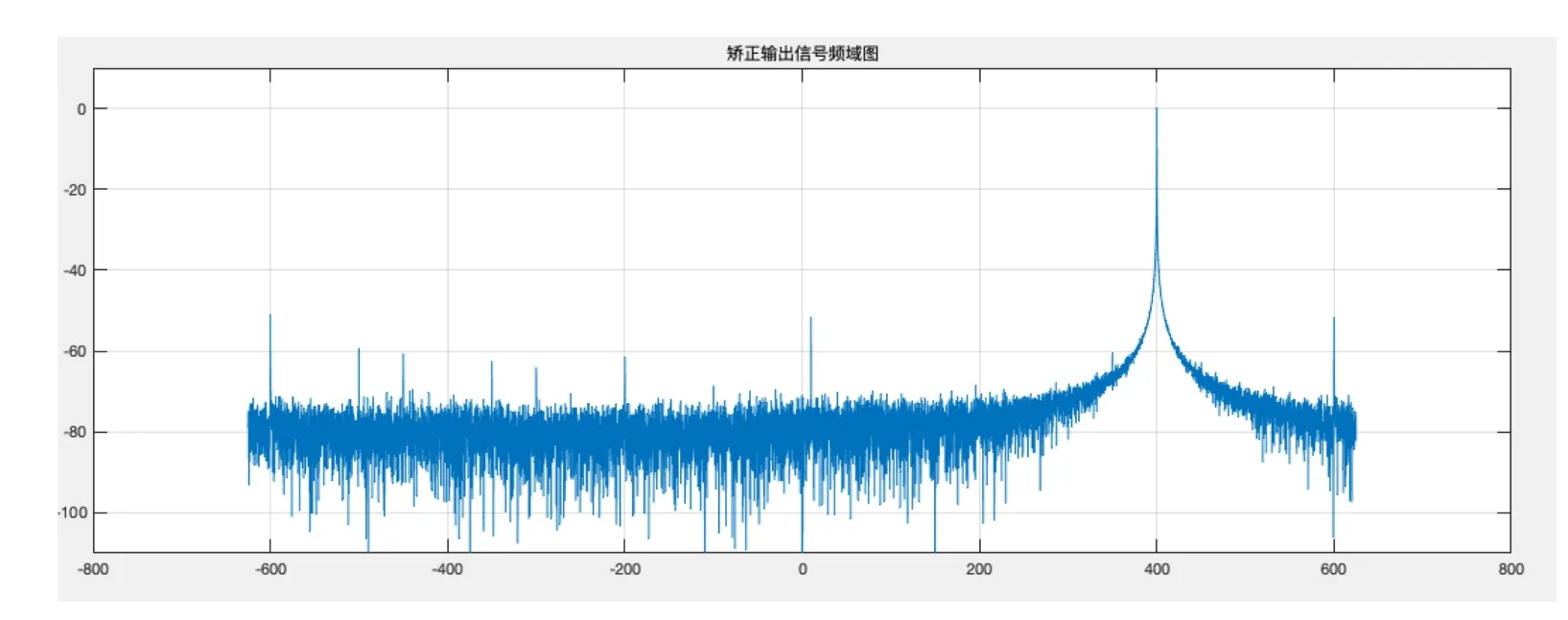
图13 矫正信号频域仿真Fig.13 Frequency Domain Simulation of Actual Data for Revised Signal

图中采用了ffshift[14]，将原始的频域图像，进行了向0频搬移的运算，以方便观测.

从观测结果可知，修正后的频域图，不但去掉了镜像，对其他毛刺也有一定能力的修正，经过多组实测数据的验证，均证明该补偿方法修正能力可行.

4 结论

本文针对I/Q不平衡进行了分析与补偿的研究，从原理出发，建立初始模型，修正模型，简化模型.针对一般集成电路运算复杂度不如上位机，但要求运算速度性能严格的现象，研究并验证了基于矩阵模型的I/Q补偿与矫正模型.并进行了预估模型的时域仿真，以及实测数据的频域仿真.时域仿真模型证明了该模型可以有效的对少量发生信号进行有效的矫正，频率仿真模型证明了对大量实测数据实验，可以有效的消除镜像，可以有效的对I/Q不平衡进行补偿，稳定通信系统的性能.

除了本文提到的分析方法外，I/Q不平衡补偿还可以使用大量的频域变换[15]，从而利用奇偶特性，共轭对称性，希尔伯特变换等特性，更加高效，稳定的获取补偿模型，在通过极限方法，简化模型，从而得到高效的修正矩阵，这也将成为以后研究补偿特性的一个重点方向.