基于X12－ARIMA和LSTM组合模型的城市蔬菜价格波动规律及预测

曹新悦，贺春林，崔梦天

(1.西南民族大学计算机系统国家民委重点实验室，四川 成都610041；2.西华师范大学计算机学院，四川 南充637009)

蔬菜价格的波动牵连生产者和消费者，关乎社会民生问题[1].农产品价格预测属于经济预测范畴，目前已有的经济预测方法有几百种，主要分为定性和定量两类[2]，定量方法成为预测者的首选，定性预测法大多作为定量研究的补充方法.定性预测主要依靠自身的经验去对未来事物的发展趋势进行描述，预测成本低，但缺乏严谨的科学数据支撑，比如:个人主观、德尔菲法等.定量预测要求大量的经济数据，并发现数据变量之间的相互关系，以此来建立相应的数学统计模型，使用模型进行预测，其预测方法可分为传统预测和智能预测[2].传统预测常用的有时间序列法、ARIMA模型等；智能预测常用的有人工神经网络、GM模型等.传统预测法在处理线性数据方面能力较强，但是在突发影响因素的情况下模型预测不理想.例如滕永平使用X12季节调整法和ARIMA模型深度研究未来一段时间我国玉米价格变化情况[3]，结果表明短期预测精度较高，受随机因素影响对中长期预测较差.智能预测法虽然具有较强的非线性数据挖掘能力，但是处理小样本数据是极容易产生过拟合、泛化能力弱等现象.彭红星等比较LSTM、BP、ARIMA三种模型对蔬菜价格短期预测比较，结果表明短期预测ARIMA模型精度最高，但是性能不如其它两者稳定[4]；Yoo TaeWoong，Oh IlSeok[5]提出了季节性长短期记忆神经网络模型(SLSTM)对农产品的销售量进行时间序列预测，研究发现该模型性能和预测精度都明显优于传统ARIMA和标准LSTM.Luyao Wang[6]等在研究农产品价格预测方法的进展和未来发展趋势中表明，季节调整可用于研究农产品价格季节性预测任务，在未来研究发展中使用混合优化算法成为提高农产品预测性能的主流.

因此，本文以成都市市场大宗蔬菜莴笋为例进行研究分析，本文建立X12－ARIMA－LSTM组合模型，其中使用X12季节调整算法剔除蔬菜价格季节性特征，用经典的ARIMA模型揭示季节调整后蔬菜价格时间序列变动的线性规律，最后用具有时间序列特性的神经网络LSTM对经过ARIMA预测的残差序列进行预测，挖掘蔬菜价格序列的非线性变化规律，组合模型的预测值等于这两部分的预测值的和[7].

1 Census X12和H－P滤波对蔬菜价格数据分解

1.1 模型概述

本文研究的对象蔬菜价格数据属于经济时间序列的范畴，对其分解主要包括季节调整和趋势分解，使用方法为Census X12和H－P滤波分析法.

使用Census X12[8]对经济时间序列数据进行研究，提取出趋势循环序列，去除季节性和不规则要素，能够达到客观分析出随着时间的发展经济指标的序列数据的发展趋势和波动特征，并依据分析的结果判断出经济时间数据的上涨和下跌波动是否受其它因素的影响，还是单纯的受季节性的变化导致.

H－P滤波[9]是将季节调整后的趋势循环周期序列分解，则:

其中:Y T t是趋势成分；Y C t波动成分.

1.2 数据来源

以成都市大宗蔬菜月度平均市场批发价格作为研究对象，数据来源于中国四川省蔬菜价格数据网成都分区，中心批发市场和龙泉聚合市场.选取的时间范围从2014年1月到2019年12月.这六年的数据作为研究数据，对实验中的缺失数据使用线性填值法填充符合实际的需求.

1.3 蔬菜价格波动特征

为明确成都市莴笋价格波动规律，深入挖掘成都市市场莴笋价格整体发展变化趋势和推动价格起伏波动的原因.借助Eviews 8.0平台，采用X12模型和H－P滤波算法，对成都市莴笋批发价格进行定量分析，实验分析结果如下:

1.3.1 价格整体上涨缓慢，年内波动幅度大

图1是经过季节调整后的莴笋价格时间序列图，用此处的X_SA表示.从图中可以看出2014～2019年，成都市大宗蔬菜产品莴笋整体的价格呈上涨趋势，但是上涨的幅度较小，但是年内价格幅度波动很大，甚至最大年内幅度差有接近四倍.据调研推动蔬菜价格总体呈上涨趋势的主要原因有:第一，农业生产成本增加(包括农业从事人员工资的上涨)，2014年到2019年农业生产资料价格指数增加了6.9%；第二，近几年国家大力发展西部地区，成都市经济持续扩展，最近6年来成都市居民价格消费指数(上年＝100)分别是101.3%、101.1%、102.2%、102%、101.4%、103.1%，这必然推动蔬菜价格呈上涨的趋势.

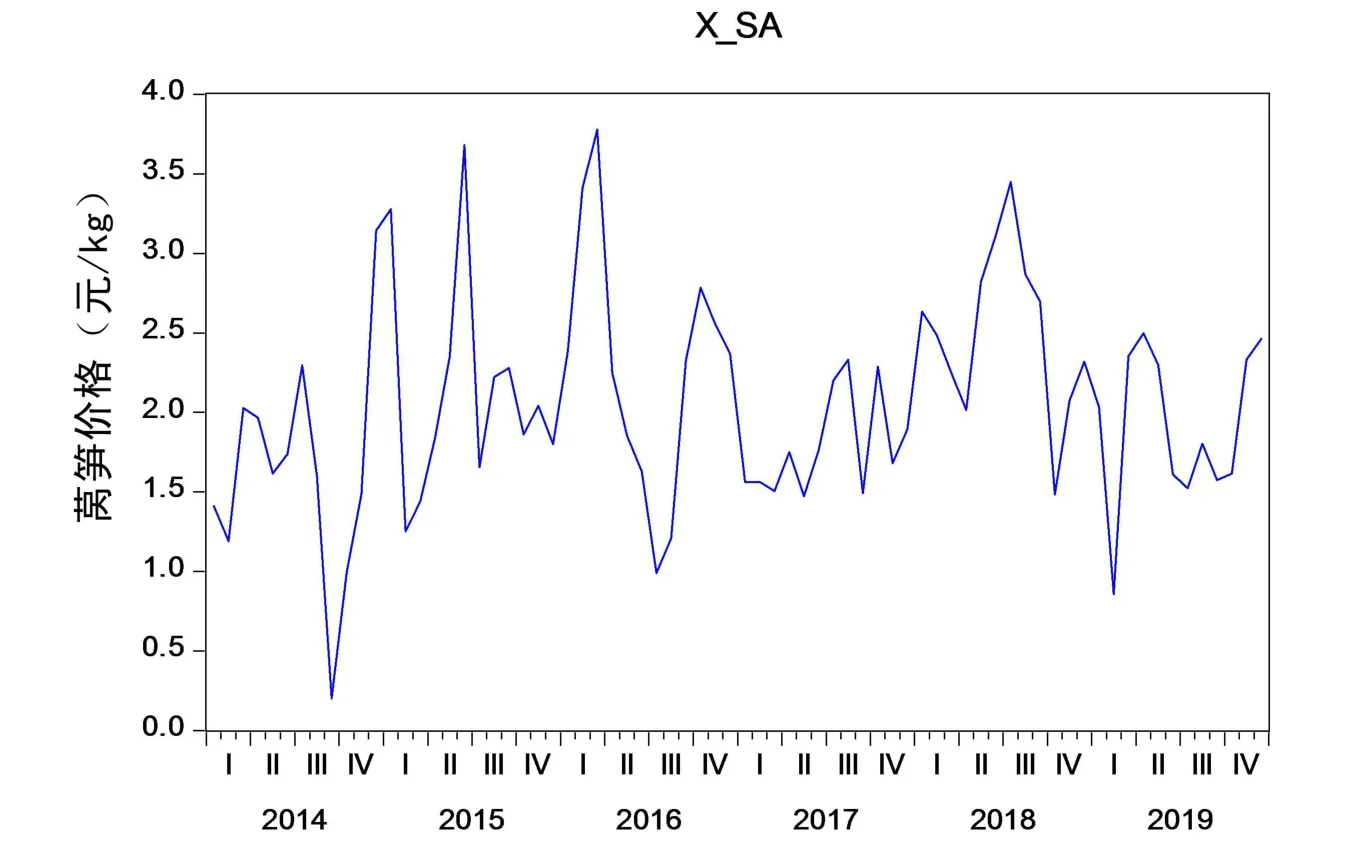
图1 莴笋价格季节调整Fig.1 Seasonal adjustment of lettuce price

1.3.2 具有明显季节波动特征

从图2中可知成都市的莴笋价格具有明显的季节波动性，年度间季节波动较为平稳，未出现扩大或缩小的趋势.从图中可以看到每年有两次峰值，分别是春节所在的2月和学生暑假对应的8月到9月，大量的国内外游客来到这个城市，蔬菜的需求自然会随之上升，价格也会达到顶峰.一次低谷是由于5月份左右是莴笋成熟的季节，大量蔬菜上市，会产生蔬菜最低价.12月份造成价格低谷的原因是外地菜的冲击以及本地其它蔬菜品种上市多造成市场莴笋价格急剧下降.

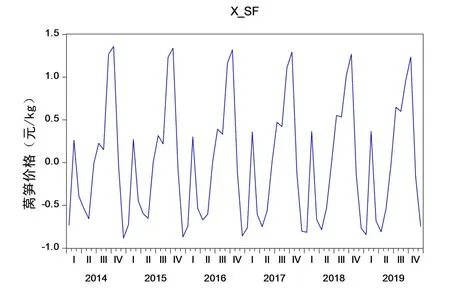
图2 莴笋价格季节性波动Fig.2 Seasonal fluctuation of lettuce price

1.3.3 受自然灾害等随机因素影响大

从图3季节调整后的莴笋价格X_IR波动序列可知，2014～2016年成都市市场莴笋价格波动频繁，且上下跨幅很大，2017～2019年波动幅度相对较小，据统计调研，对于成都市蔬菜来说，受随机因素冲击波动大的时期都与气象、疫情、自然灾害等突发事件有关，因为这些因素直接关乎蔬菜的上市量，牵连着市场蔬菜供需平衡问题.例如2014年该省经历了泥石流、洪涝等自然灾害，全年自然灾害率达到最近几年最高值，该年蔬菜上市量骤降.

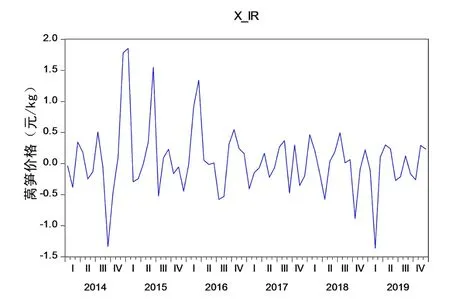
图3 莴笋价格不规则变化Fig.3 The price of lettuce changes irregularly

1.3.4 价格波动具有周期循环性

剔除了不规则因子和季节因子后，将循环趋势序列使用H－P滤波分析法分解为趋势项(T)和循环项(C).莴笋价格具有长期线性上涨的趋势(图4所示)，上涨的趋势较为缓慢，同时可以明显看到莴笋价格变化具有周期性，2014年1月至2019年12月之间有两个周期(见表1)，波长大致为两年半，具有两涨两跌(一大涨一小涨)的特点.

表1 莴笋价格波动周期Table 1 lettuce price fluctuation cycle

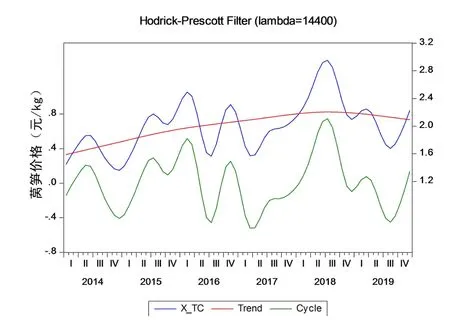
图4 莴笋价格趋势循环变化Fig.4 Cyclic change of lettuce price trend

2 蔬菜价格预测

2.1 X12－ARIMA和LSTM组合预测思想

在短期时间序列预测模型中，计量统计方法X12－ARIMA[10]是非常经典的一种，具有较高的预测精度，但是它有一个很大的缺点，只适用于解决线性问题，当需要处理的问题不是完全线性关系时，将会出现较大偏差.LSTM[11－13]神经网络能够实现对时序性、非线性数据进行长期记忆循环网络功能研究，但是面对小样本数据易出现泛化能力弱，过拟合等现象，对数据集的要求比较高，模型结构复杂[14－15].本文研究的成都市市场莴笋月平均价格数据是小样本集，受不规则冲击影响大，具有季节性、非平稳等特征，采用单一模型预测误差大，使用两者组合模型，达到优势互补的效果.

2.2 X12－ARIMA模型建立与预测

2.2.1 X12－ARIMA建模的步骤

首先，使用X12季节调整模型对成都市莴笋价格原始序列Y(t)进行分解，得到序列数据Y(t_sa)，然后ARIMA对Y(t_sa)建模.建模的关键步骤有:分析序列的ADF值、确定p、d、q的值、估计AR和MA的相关系数、检验白噪声序列是否存在相关性、完成预测模型[16].

2.2.2 序列平稳性检验

成都市莴笋价格时间序列为Y(t)，经X12季节调整后的价格序列为Y(t_sa)，使用ADF检验法对Y(t_sa)进行单位根检验，进一步判断其平稳性，如下表2所示，季节调整后的莴笋价格序列在百分之一、百分之五、百分之十的条件下都是平稳的，因此，无需对季节调整后成都市莴笋价格序列进行差分处理，可以直接作为输入数据进行ARIMA(p，d，q)模型建模，d＝0.

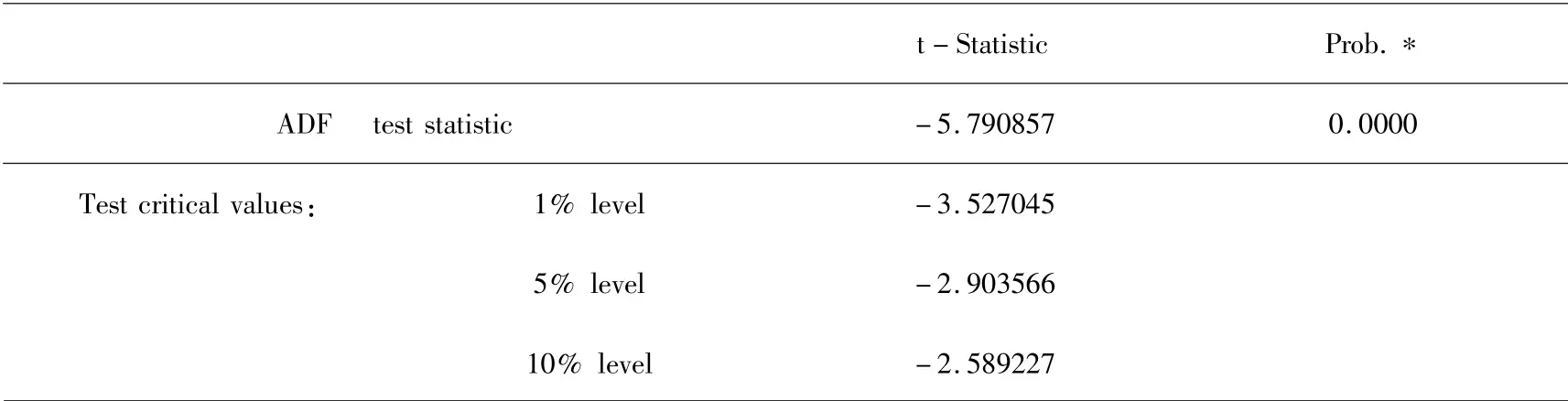
表2 季节调整后的ADF检验Table 2 ADF test after seasonal adjustment

2.2.3 ARIMA模型的建立

建立ARIMA(p，d，q)模型需要确定三个参数，由上面ADF检验可知，序列平稳d＝0，偏自相关系数p和自相关系数q确定根据实验的自相关系数图结果以及参考赤池信息准则(AIC)较小为优准则进行确定[8]，使用检验统计量D.W.对残差序列进行检验.如下表3所示实验结果数据可知，自相关滞后一阶、偏自相关滞后二阶，AIC准则取值最小，残差序列检验统计量D.W.接近2，说明创建的模型拟合度最高、性能最优.

由表3的实验参数数据，可写出X12－ARIMA(其中p＝1，d＝0，q＝2)的预测模型公式:

表3 检验结果Table 3 Test results

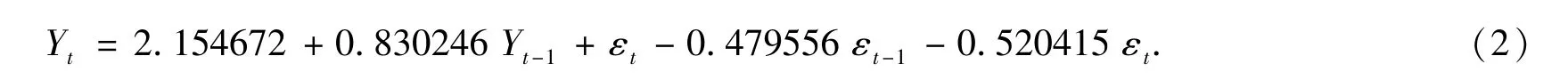
该模型对成都市市场莴笋价格拟合及预测如图 5所示(莴笋价格:元/kg).

图5 X12－ARIMA莴笋价格拟合图Fig.5 Price fitting diagram of X12－ARIMA lettuce

2.3 LSTM模型建立与预测

2.3.1 数据集处理

将收集的成都市市场莴笋月平均价格按日期排好序，训练集和测试集的选取按照蔬菜价格时间序列数据2:1的要求分配.

2.3.2 训练模型及参数设置

采用karas库构建模型，由于实验数据集较小，经过不断的实验调参，最终确定较为合适的实验结构情况为:隐藏层为三层，其中每层神经元的个数为128个，使用Relu函数对每个网络进行非线性处理，输入维度和输出维度都为一；使用Adam优化函数，MSE作为模型的损失函数，选择Dropout为0.01训练迭代100次，batch_size为18.如图6所示该模型对2014年到2019年市场莴笋价格的拟合及未来半年的预测，整体预测趋势与真实趋势基本一致，正确率达到85%.

图6 LSTM莴笋价格拟合图Fig.6 Price fitting diagram of lettuce in LSTM

2.4 X12－ARIMA－LSTM模型建立与预测

把成都市市场莴笋月平均价格的时间序列Y t看成线性结构f t和非线性结构S t组成.即:Yt＝f t＋S t.

2.4.1 具体步骤

步骤1:使用X12－ARIMA模型对原始莴笋价格序列进行预测，得到预测值.步骤2:用真实值减去得到误差序列，再用LSTM模型预测误差序列，得到预测值.步骤3:组合模型X12－ARIMA－LSTM的预测值等于步骤一和步骤二这两步预测值的和，，即:.

2.4.2 预测结果分析

为考察以上三种模型对莴笋价格数据各自预测效果，选择MAPE作为衡量的标准[17].

在处理同样的研究对象情况下，三种模型对时间序列数据预测的结果如表4所示.从预测精度维度分析，组合模型的预测精度平均误差11.3%、神经网络模型LSTM平均误差为15.7%、最差的是计量统计模型X12－ARIMA模型平均误差为21.1%；从模型稳定性的角度分析，组合模型的误差范围4.2%～15.7%、LSTM模型的误差范围5%～24.5%、X12－ARIMA模型的误差范围0.0%～50%，可以看出组合模型的稳定性最高，传统模型性能稳定性最差.综上可得结论:三种模型的预测效果按大小依次排序，分别是X12－ARIMA－LSTM组合模型、LSTM模型以及X12－ARIMA模型，在现实生活中可以选择组合模型作为对经济时间序列数据研究的可靠工具.

表4 不同模型下的莴笋价格预测Table 4 Lettuce price forecast under different models

2019.082.402.400.02.208.02.104.22019.092.543.0018.12.0021.32.1415.72019.102.853.088.13.005.33.005.32019.112.161.7618.52.515.72.4513.42019.121.721.3223.32.122.11.9513.4 MAPE 21.115.711.3

3 结论

蔬菜价格波动具有线性和非线性两种特征，使用传统模型对处理非线性问题能力较弱；智能预测方法虽在非线性、自适应学优化算法等方面的优势，但是面对小样本集容易产生过拟合，导致模型预测精度不高.组合模型结合了各自的优势，能提高预测精度、把握成都市莴笋价格变动趋势，更适合作为时间序列价格数据的研究方法.