基于季节性ARIMA模型的入境旅游市场预测模型构建*

孙 颖

(安徽工程大学)

0 引言

入境旅游能够增加外汇收入、扩大就业机会、减少贫困、促进经济增长、提升区域品牌形象，因此，在旅游业中具有重要的地位.入境旅游逐渐成为区域竞争力和旅游发展综合实力的指标之一.

国外相关研究偏重于旅游市场的影响因素(Kevin Greenidge[1]；Kwabena Aaman，Rose Ismail[2]；Christine Lim[3])、需求预测(Chao-hung Wang[4]；Vincent Cho[5]；Kima，Moosab[6]).国内已有研究偏重于旅游需求(宋章海[7]；刘富刚[8])、旅游市场需求预测(孙根年[9]；殷英等[10]；黄金华[11]；李琳[12])、旅游市场现状特征(王冬萍[13]；朱强华, 冯学钢[14]；余瑞林、张红[15]；李静[16]).

总体来说，国外对旅游市场的研究较重视旅游需求分析与预测，国内研究主要以具体城市或地区为研究对象，以中国旅游市场为研究对象的较为罕见.在经济新常态下，分析和预测中国入境旅游市场对于经济社会的发展具有重要的现实意义.因此，该文以中国旅游市场为实证研究对象，建立季节性ARIMA模型并检验，以构建中国入境旅游市场的最优预测模型.

1 数据来源及特征分析

1.1 数据来源

选取中国入境旅游市场作为实证研究对象，鉴于数据的可获得性，实证样本范围为1999～2015年12月中国入境旅游人数的月度数据(单位：万人次)，序列记为MVA，数据全部来自于《中国旅游统计年鉴》.

1.2 描述性分析

为更好地分析序列特征，绘制样本数据的趋势图，如图1所示.

观察图1可知，1999～2015年间，中国入境旅游人数在数量上呈不断上升走势，由1999年1月的545.94万人次上升到2015年12月的1171.9万人次.从走势上看，该序列呈现出明显的季节性和周期性.那么，中国入境旅游人数的走势具体特征及未来趋势如何？需进一步做实证研究.

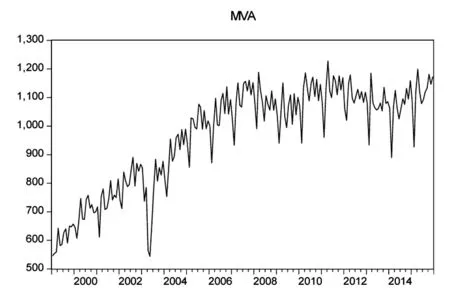
图1 入境旅游人数时间序列图

2 模型构建

2.1 模型定阶

时间序列的平稳性直接影响模型的构建和结果的可靠性.仅从趋势图无法判断序列的平稳性，因此，采用ADF检验法分析序列MVA的平稳性，结果见表1.

表1 序列MVA的ADF检验结果

由表1可知，序列MVA的ADF值远大于1%、5%、10%检验水平下的临界值，其概率P=0.8043，因此，可以判断序列MVA是非平稳的.为进一步观察其特性，绘制相关图和Q统计量，如图2所示.

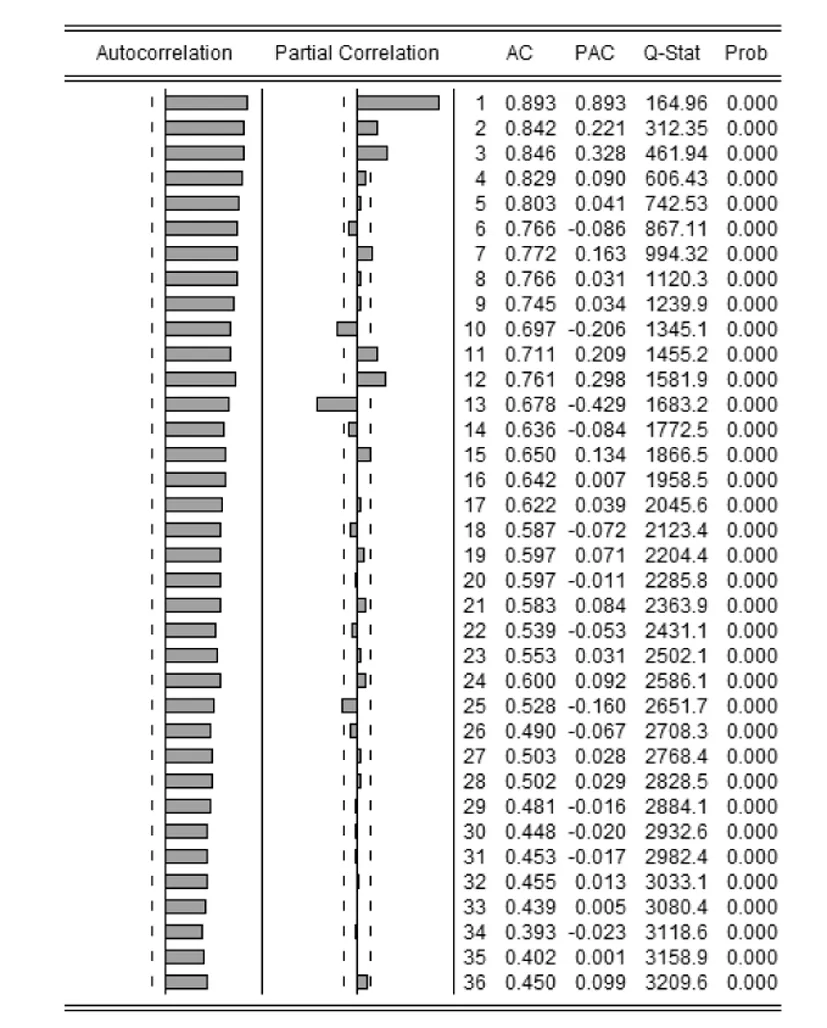
图2 序列MVA的相关图和Q统计量

观察图2可知，序列MVA的自相关函数呈指数衰减趋势，衰减速度非常慢，由此也可以确定序列为非平稳序列.另外，图2并未显示出序列MVA的季节性，这可能是由于序列长期趋势掩盖了自相关函数的季节性.因此，需对序列MVA做一阶自然对数差分以分析其季节性并减小波动性.一阶自然对数差分后的序列记为M.首先检验序列M的平稳性，结果见表2.

由表2的数据结果显示，序列M为平稳序列.进一步做序列M的相关图和Q统计量，结果如图3所示.

表2 序列M的平稳性检验结果

由图3可知，序列M的自相关函数衰减较快，且呈现出一定的季节性，在滞后1阶、6阶、12阶、18阶、24阶、30阶、36阶均超出了95%的置信区域，因此，首先对序列M进行步长为6的季节差分，生成的新序列记为SM.做序列SM的相关图，如图4所示.

图3 序列M的相关图和Q统计量

由图4可知，序列SM的自相关函数在滞后12阶处显著地不为零，其他各阶均在95%的置信区域内，说明序列的季节性已基本消除.

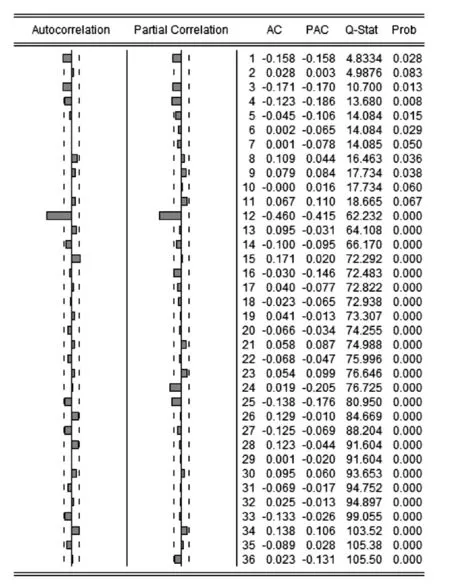
图4 序列SM的相关图和Q统计量

由以上分析可得到ARIMA(p,d,q)(P,D,Q)12模型的基本形式.在ARIMA(p,d,q)(P,D,Q)12模型中，p=12，d=1，q=1，P=1，D=1，Q=1或0，因此，建立ARIMA(12,1,1)(1,1,1)12模型或者ARIMA(12,1,1)(1,1,0)12模型.

2.2 模型估计

对所建立的模型分别进行估计，以判断模型的可靠性.首先，ARIMA(12,1,1)(1,1,1)12模型的估计结果如图5所示.

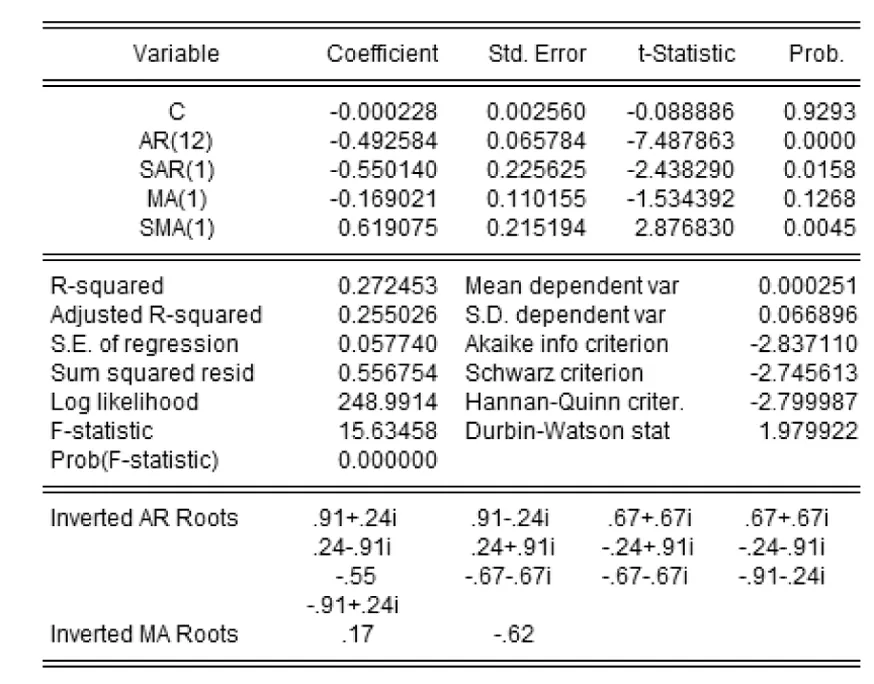
图5 ARIMA(12,1,1)(1,1,1)12模型估计结果

由图5可知，AR过程的13个复根的模均小于1，MA过程的2个实数根的模也均小于1.由此可判断ARIMA(12,1,1)(1,1,1)12模型平稳且可逆.

同理，ARIMA(12,1,1)(1,1,0)12模型的估计结果如图6所示.

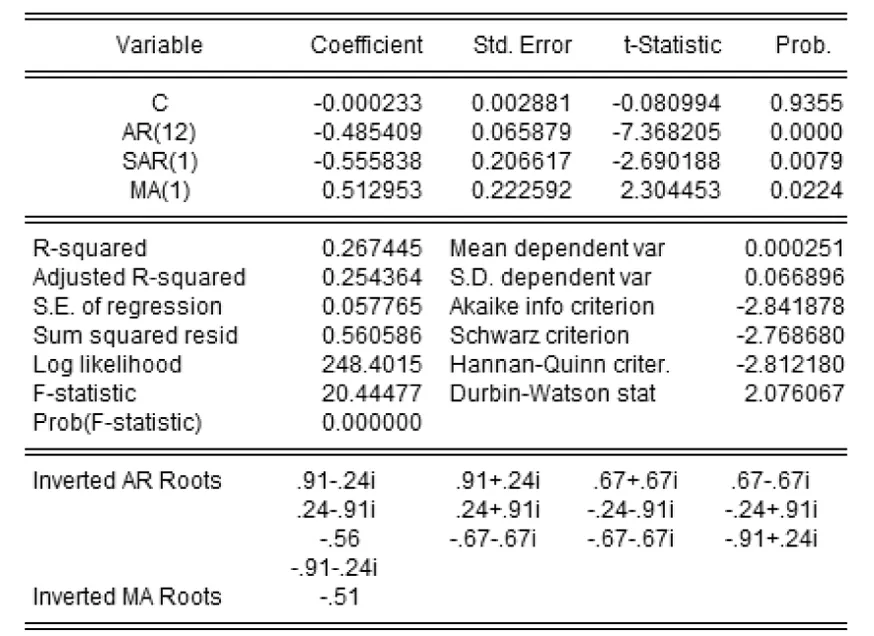
图6 ARIMA(12,1,1)(1,1,0)12模型估计结果

由AR过程和MA过程的根的模可以判断ARIMA(12,1,1)(1,1,0)12模型也是平稳且可逆的.两模型均为有效模型，对二者做进一步比较分析，以选择最优模型.主要采用R2、AIC准则和SC准则进行判断，结果见表3.

表3 两模型的比较结果

进一步比较可知，ARIMA(12,1,1)(1,1,0)12模型的AIC准则和SC准则更小，同时，该模型更简洁，因此，ARIMA(12,1,1)(1,1,0)12模型为更优模型.

2.3 残差检验

模型检验采用残差检验法.当残差为白噪声序列时，所建立的模型有效，否则，拟合模型无效.对ARIMA(12,1,1)(1,1,0)12模型估计结果的残差做白噪声检验，结果如图7所示.

图7的结果显示，残差序列的P值均大于0.05，自相关函数均在95%的置信区间内，因此，残差不存在相关关系.从而表明ARIMA(12,1,1)(1,1,0)12模型显著有效.

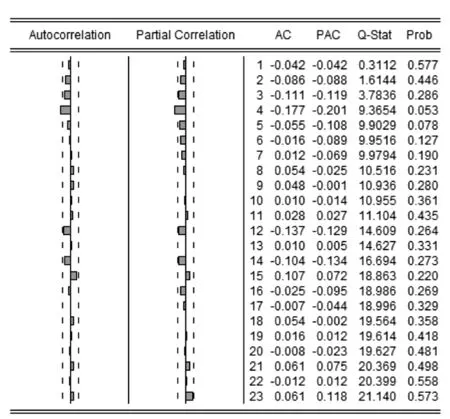
图7 最优模型估计结果的残差检验

2.4 模型拟合

采用ARIMA(12,1,1)(1,1,0)12模型对中国2015年7～12月的入境旅游人数进行拟合，结果如图8所示.

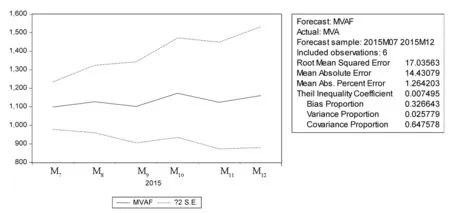
图8 2015年下半年的入境旅游人数拟合值

将模型拟合得到的数据及实际值整理并进行比较分析，见表4.

表4 模型拟合值与实际值的比较结果

由表4可知，ARIMA(12,1,1)(1,1,0)12模型的拟合结果与实际值的误差均小于5%，说明模型拟合精度较高，且误差并未随着预测期的增加而增大.综上，ARIMA(12,1,1)(1,1,0)12模型可以作为中国入境旅游人数预测的最优模型，该模型预测精度和准确性均较高.

3 结论

鉴于数据的可获得性，该文基于1999年1月～2015年12月中国入境旅游人数的月度数据，构建了中国入境旅游市场预测模型并检验.实证结果表明，ARIMA(12,1,1)(1,1,0)12模型为最优模型，可以为相关部门的政策措施制定提供新的思路和依据，并为进一步分析和更好地服务于中国入境旅游市场提供一定的理论依据.