考虑路径可靠性的垃圾回收选址路径问题研究

史志学 李锐

摘要：  在路径中断情况下，为了降低垃圾回收成本和提高收集路径的安全性，本文主要对基于路径可靠性的垃圾回收选址路径问题进行研究。建立了带有车辆路径可靠性约束的选址路径问题优化模型，在路径可靠性水平满足要求的条件下，最小化回收物流总成本。根据问题模型的特点设计粒子群优化（particle swarm optimization， PSO）算法求解，为了验证模型的合理性和算法的有效性，采用Matlab软件编程，对不同的数值算例进行仿真测试，并且分析路径可靠性水平对成本的影响。实验结果表明，该模型能够对问题进行合理描述，粒子群优化算法能够对不同规模的问题进行有效求解，并且随着可靠性水平的增大，总成本增加，开设成本无明显变化，车辆运营成本增加，运输和处理成本增加。该研究对提高垃圾回收系统的可靠性具有重要意义。

关键词：  垃圾回收; 选址路径问题; 路径可靠性; 粒子群优化算法

中图分类号： TP29  文献标识码： A

收稿日期： 20210331; 修回日期： 20210617

基金项目： 辽宁省自然科学基金指导计划项目（20180550300）; 辽宁省教育厅青年科技人才“育苗”项目（JQL202015407）

作者简介：  史志学（1996），男，江苏徐州人，硕士研究生，主要研究方向为物流网络设计和智能优化。

通信作者：  李锐（1985），男，辽宁海城人，博士，副教授，硕士生导师，主要研究方向为智能计算和物流优化。 Email： 279496574@88.com

垃圾是环境污染的重要来源之一，为有效缓解环境污染，长期以来，垃圾回收一直是各个国家亟待解决的问题。对于压缩车直运模式下的垃圾回收，垃圾综合处理中心的合理选址及车辆路径的优化有利于节约回收成本。随着安全意识的增强，人们不仅关注垃圾回收的物流成本，还需要关注垃圾回收过程中路径中断对回收系统造成的影响。因此，考虑路径可靠性的垃圾回收网络对于垃圾回收的可持续性具有重要意义。近年来，国内外学者对各种选址路径问题（locationrouting problem，LRP）进行了研究。C.Prodhon等人[1]对LRP的最新进展进行了综述，包括经典LRP的求解以及各种LRP的扩展;M.Schneider等人[2]对标准LRP的不同求解方法进行了详细的综述;胡大伟等[3]主要对LRP的扩展问题相关研究进行了介绍。目前，逆向物流LRP更加引起关注。Hong L等人[4]对多目标逆向物流LRP进行了研究;V.R.Ghezavati等[5]研究了带有时间窗的逆向物流LRP;Hong L等人[6]对带有灰色回收需求的逆向物流LRP进行了研究;Zhao J等人[7]对爆炸性废弃物回收LRP进行了研究;J.S.Kim等人[8]研究回收物流网络设计问题集成LRP模型;乔佩利等人[9]对第三方逆向物流LRP问题进行了研究;李昌兵等人[10]研究集成库存的逆向LRP;Li H等人[11]研究城市固体废弃物回收LRP;M. Rabbani等人[12]研究工业危险废弃物回收LRP。虽然当前国内外学者对LRP进行了大量的研究，但对于考虑可靠性的LRP研究较少。Zhang Y等人[13]利用基于情景的规划方法对考虑随机中断的LRP进行研究;Xie W等人[14]研究设施以概率中断的可靠性LRP;A.Ahmadijavid等人[15]研究考虑随机的生产配送中心和车辆的中断风险下的LRP;F.Rayat等人[16]研究考虑配送中心的供应中断和集成库存的可靠性LRP。以上研究均未考虑中断的逆向物流LRP。基于此，本文研究考虑路径可靠性的垃圾回收物流选址路径优化问题，建立垃圾回收选址路径优化模型，在路径可靠性水平满足要求的条件下，最小化回收物流总成本，根据问题模型特点设计粒子群优化算法求解，通过实验来验证模型的合理性及算法的有效性。本研究对垃圾回收具有一定的实际应用价值。

1 问题描述及模型建立

压缩车直运模式下的回收系统包括垃圾收集点、综合处理中心、垃圾压缩车和收集线路4部分。垃圾压缩车从综合处理中心出发依次通过不同的垃圾收集点进行垃圾收集，然后返回原综合处理中心，进行填埋、堆肥或焚烧等废弃处理。考虑路径可靠性的垃圾回收LRP，建立带有车辆路径可靠性约束的LRP优化模型，通过选择开设综合处理中心及确定不同车辆的行驶路径，在满足可靠性要求水平的条件下，最小化系统总成本。优化模型的假设条件如下：

1） 垃圾收集点的位置和数量已知。

2） 候选的综合处理中心的位置和数量已知。

3） 任意一个垃圾收集点必须有且只有一辆压缩车服务。

4） 每辆压缩车只能从一个综合处理中心出发，并返回该综合处理中心。

5） 每个综合处理中心允许多个车辆驶出和驶入。

1.1 符号及变量

为了问题模型的建立，引入以下符号。N=J∪L表示节点集合，其中L表示收集点集合，J表示综合处理中心集合;V表示收集车辆集合;Dl表示收集点l∈L的收集量;Gj表示綜合处理中心j∈J的开设成本;Uj表示综合处理中心j∈J的处理能力;Pj表示综合处理中心j∈J的单位处理成本;Rj表示综合处理中心j∈J的可靠性;Fv表示车辆v∈V的固定运营成本;Qv表示车辆v∈V的运输能力;Cab表示从点a∈N到点b∈N的固定运输成本;rab表示从点a∈N到点b∈N的可靠性。

决策变量定义如下：xabv∈0，1表示如果车辆v∈V从点a∈N到点b∈N，取值为1，如果车辆v∈V没有从点a∈N到点b∈N，取值为0;yjv∈0，1表示如果车辆v∈V服务于综合处理中心j∈J取值为1，如果车辆v∈V不服务于综合处理中心j∈J取值为0;zj∈0，1表示如果开设综合处理中心j∈J取值为1，如果没有开设综合处理中心j∈J则取值为0。决策变量xabv、yjv和zj对应的向量分别定义如下：X=xabv|a，b∈M，v∈V，Y={yjv|j∈J，v∈V}，Z={zj|j∈J}。

1.2 优化模型

基于以上符号和变量说明，考虑路径可靠性的垃圾回收选址路径优化模型为

minf（X，Y，Z）=∑j∈JGjzj+∑v∈V∑j∈JFvyjv+∑j∈JPj∑v∈V∑l∈L∑b∈NDlxlbvyjv+∑a∈N∑b∈N∑v∈VCabxabv（1）

s.t.

∏j∈JRjyjv∏a∈N∏b∈Nrabxabv≥β   v∈V（2）

∑l∈Lxjlv-yjv=0   j∈J，v∈V（3）

∑v∈V∑l∈Lxjlv-zj≥0   j∈J（4）

∑l∈Lxjlv-zj≤0   j∈J，v∈V（5）

∑b∈Nxabv-∑b∈Nxbav=0   a∈N，v∈V（6）

∑a∈W∑b∈Wxabv≤W-1   WL，W≥2，v∈V（7）

∑j∈J∑l∈Lxjlv≤1   v∈V（8）

∑v∈V∑b∈Nxlbv=1   l∈L（9）

∑v∈Vxabv=0   a，b∈J（10）

∑l∈L∑b∈NDlxlbv≤Qv   v∈V（11）

∑v∈V∑l∈L∑b∈NDlxlbvyjv≤zjUj   j∈J（12）

xabv∈0，1   a，b∈N，v∈V（13）

yjv∈0，1   j∈J，v∈V（14）

zj∈0，1   j∈J（15）

目标函数表达式（1）为最小化物流总成本，包括综合处理中心的固定开设成本、车辆的固定运营成本、处理成本和运输成本;式（2）为车辆路径的可靠性约束，β为要求的可靠性水平;约束（3）表示车辆v服务于综合处理中心j;约束（4）表示如果综合处理中心开设，那么必须有车辆驶出;约束（5）表示没有开设的综合处理中心，则没有车辆驶出;约束（6）表示车辆从某收集点或综合处理中心驶入，也要从该点驶出;约束（7）表示收集点之间不能形成子环路;约束（8）要求每辆车最多服务一个综合处理中心;约束（9）要求每个收集点必须有且只有一个车辆服务;约束（10）保证在任意两个综合处理中心之间没有车辆;式（11）为车辆的运输能力约束;式（12）为综合处理中心的能力约束;式（13）～（15）为二值变量约束。

2 算法设计

考虑路径可靠性的垃圾回收选址路径问题是经典LRP的扩展，所以也是NPhard问题。当规模较大时，问题求解困难，所以设计智能优化算法对该问题进行求解。粒子群优化算法是一种经典的群智能优化算法[17]。目前，PSO算法已经得到广泛应用，如作业车间调度问题[18]、目标特征选择[19]、云计算资源调度问题[20]等。本文根据问题特点设计粒子群优化算法进行求解，采用实数编码方式进行编码。

2.1 算法的主要步骤

PSO的主要步骤如下：

Step 1：种群初始化。随机生成初始的位置X1，X2，…，XN和速度V1，V2，…，VN。

Step 2：计算每个粒子的适应值。

Step 3：更新粒子i的历史最好位置Pti和全局最好位置Ptg。

Step 4：按照下式更新粒子的速度和位置，即

Vt+1ij=wVtij+c1·r1Ptij-Xtij+c2·r2Ptgj-Xtij（16）

Xt+1ij=Xtij+Vt+1ij（17）

其中，Vtij为粒子i第j维第t代的运动速度;Ptij为粒子i历史最好位置的第j维;Ptgj为全局最好位置的第j维;r1和r2为0，1之间的随机数;c1和c2为加速度常数;w为惯性系数。

Step 5：如果达到最大迭代次数，则终止循环，并输出最优解;否则，转到Step 2。

2.2 解的编码与解码

实数向量对应问题的解。向量包括3个部分，第1部分表示垃圾收集點的排序，每一位对应一个垃圾收集点，取值为0，1之间的实数，根据取值可以得到垃圾收集点的排序;第2部分表示各个垃圾收集点的车辆分配，每一位取值范围为1，NV，对应的整数表示选择的车辆号，NV为车辆数;第3部分表示车辆所分配的综合处理中心，每一位对应一个车辆，取值为1，NK之间实数，对应的整数表示车辆选择的处理中心，NC为垃圾收集点数量，NK为综合处理中心数量。

2.3 适应值函数

给定粒子位置Xi，通过解码得到解X，Y，Z，并计算粒子适应值为

C=f（X，Y，Z）+α1β-∏j∈JRjyjv∏a∈N∏b∈Nrabxabv++α2∑v∈V∑l∈L∑b∈NDlxlbv-Qv++α3∑j∈J∑v∈V∑l∈L∑b∈NDlxlbvyjv-zjUj+（18）

式中，f（X，Y，Z）为目标函数（1），可靠性约束（2）和能力约束（11）和（12）作为惩罚项加入评价函数中;α1，α2和α3为惩罚系数，取值为很大的正数;·+表示如果括号内值为正则取该值，否则取0。

3 实验及结果分析

为了验证模型的合理性和算法的有效性，对不同的数值算例进行测试。算法通过Matlab编程实现，并且所有测试的实验环境为Intel Core i5 CPU 2.70 GHz，内存8 GB计算机，操作系统Windows 7。

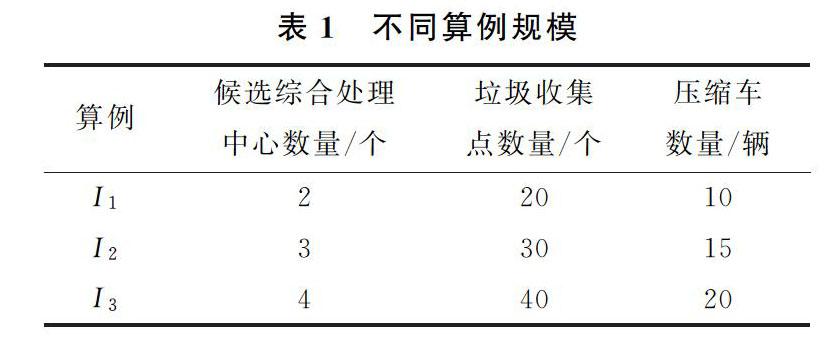
不同算例规模如表1所示。算例的参数按照均匀分布产生：收集点的收集量Dl～U[150，200];综合处理中心的开设成本Gj～U[40 000，60 000];综合处理中心的处理能力Uj～U[4 000，5 000];综合处理中心的单位处理成本Pj～U[1，10];综合处理中心的可靠性Rj～U[0.9，1];车辆的固定运营成本Fv～U[5 000，8 000];车辆的运输能力Qv～U[1 500，2 000];从点a到点b的固定运输成本Cab～U[800，1 800];从点a到点b的可靠性rab～U[0.9，1]。

首先，通过求解不同规模算例I1～I3，对PSO的性能进行测试，对于每个算例，算法分别运行10次。PSO算法的种群规模为50，最大迭代次数为100，惯性系数w取值为0.8，加速度常数c1和c2取值为1.2。不同规模算法求解结果如表2所示示，不同规模算例详细结果如表3所示，不同算例详细车辆路径如表4所示。

由表2可以看出，对于不同规模的算例，PSO算法的标准方差在1.2%～4.9%之间变化，并且随着问题规模的增加，PSO算法性能稳定，因此PSO算法能够对问题进行有效求解。表3给出了算例I1～I3各种成本。表4给出了算例I1～I3的车辆路径。

为研究路径可靠性水平对成本的影响，以算例I1为例进行实验。在不同可靠性水平下，算例I1各种成本变化情况如图1所示。由图1可以看出，随着可靠性水平增大，总成本增加，开设成本无明显变化，车辆运营成本增加，运输和处理成本增加。

4 结束语

鉴于目前对于逆向物流LRP的研究均未考虑路径可靠性，本文对压缩车直运模式下考虑路径可靠性的垃圾回收LRP进行研究。建立带有路径可靠性约束的垃圾回收LRP优化模型，设计PSO算法求解，并通过不同规模的数值算例进行仿真实验。实验结果表明，对于不同规模的问题，PSO算法能够有效求解，并保持性能稳定。根据可靠性水平的影响分析发现，随着可靠性水平的增加，总成本增加，其中车辆运营成本及运输和处理成本是导致总成本增加的重要因素。因此，要得到路径可靠性较高的回收网络需要增加成本投入。本文的研究为压缩车直运模式下考虑路径可靠性的垃圾回收系统选址路径优化提供了有效的参考模型和求解算法。对于垃圾回收系统的有效运作和安全性的提高具有重要意义。

参考文献：

[1] Prodhon C， Prins C. A survey of recent research on locationrouting problems[J]. European Journal of Operational Research， 2014， 238（1）： 117.

[2] Schneider M， Drexl M. A survey of the standard locationrouting problem[J]. Annals of Operations Research， 2017， 259（1）： 389414.

[3] 胡大伟， 陈希琼， 高扬. 定位-路径问题综述[J]. 交通运输工程学报， 2018， 18（1）： 111129.

[4] Hong L， Wang W， Zhang Q. Multiobjective locationrouting problem of reverse logistics based on GRA with entropy weight[J]. Grey Systems Theory & Application， 2012， 2（2）： 249258.

[5] Ghezavati V R， Beigi M. Solving a biobjective mathematical model for locationrouting problem with time windows in multiechelon reverse logistics using metaheuristic procedure[J]. Journal of Industrial Engineering International， 2016， 12（4）： 469483.

[6] Hong L， Zhang Q， Wang W. Research on locationrouting problem of reverse logistics with grey recycling demands based on PSO[J]. Grey Systems Theory and Application， 2011， 1（1）： 97104.

[7] Zhao J， Ke G Y. Incorporating inventory risks in locationrouting models for explosive waste management[J]. International Journal of Production Economics， 2017， 193： 123136.

[8] Kim J S， Lee D H. An integrated approach for collection network design， capacity planning and vehicle routing in reverse logistics[J]. Journal of the Operational Research Society， 2015， 66： 7685.

[9] 喬佩利， 王娜. 考虑逆向物流第三方配送的选址路径问题研究[J]. 计算机工程与应用， 2017， 53（10）： 5560.

[10] 李昌兵， 张斐敏. 集成选址—路径—库存问题的逆向物流网络优化[J]. 计算机集成制造系统， 2014， 20（7）： 17931798.

[11] Li H， Ma Z， Wang C. The stochastic locationroutinginventory problem in reverse logistics systems for municipal solid waste[C]∥Eighth International Conference of Chinese Logistics & Transportation Professionals， Chengdu， China： ASCE， 2008.

[12] Rabbani M， Heidari R， Yazdanparast R. A stochastic multiperiod industrial hazardous waste locationrouting problem： integrating nsgaii and monte carlo simulation[J]. European Journal of Operational Research， 2019， 272（3）： 945961.

[13] Zhang Y， Qi M， Lin W， et al. A metaheuristic approach to the reliable location routing problem under disruptions[J]. Transportation Research Part Elogistics and Transportation Review， 2015， 83（11）： 90110.

[14] Xie W， Ouyang Y， Wong S C， et al. Reliable locationrouting design under probabilistic facility disruptions[J]. Transportation Science， 2016， 50（3）： 11281138.

[15] Ahmadijavid A， Seddighi A H. A locationrouting problem with disruption risk[J]. Transportation Research Part Elogistics and Transportation Review， 2013， 53（1）： 6382.

[16] Rayat F， Musavi M M， Bozorgiamiri A， et al. Biobjective reliable locationinventoryrouting problem with partial backordering under disruption risks： a modified AMOSA approach[J]. Applied Soft Computing， 2017， 59（6）： 622643.

[17] Shi Y H， Eberhart R C. A modified particle swarm optimizer[C]∥Evolutionary Computation Proceedings， Piscataway， USA： IEEE， 1998.

[18] 劉洪铭， 曾鸿雁， 周伟， 等. 基于改进粒子群算法作业车间调度问题的优化[J]. 山东大学学报： 工学版， 2019， 49（1）： 5762.

[19] 王金杰， 李炜. 混合互信息和粒子群算法的多目标特征选择方法[J]. 计算机科学与探索， 2020， 14， 136（1）： 88100.

[20] 赵宏伟， 李圣普. 基于粒子群算法和RBF神经网络的云计算资源调度方法研究[J]. 计算机科学， 2016， 43（3）： 113117.

LocationRouting Problem of Waste Recycling with Routing Reliability Considered

SHI Zhixue， LI Rui

（School of Electronics and Information Engineering， Liaoning University of Technology， Jinzhou 121001， China）

Abstract：  In order to reduce the cost of waste recycling and improve the security of collection route under the condition of route disruption， this paper mainly studies the locationrouting problem of waste recycling based on route reliability. An optimization model of locationrouting problem with vehicle routing reliability constraints is established， which minimizes the total cost of recycling logistics under the condition that the routing reliability level meets the requirements. According to the characteristics of the problem model， particle swarm optimization （PSO） algorithm is designed to solve the problem. In order to verify the rationality of the model and the effectiveness of the algorithm， Matlab software is used to program and simulate different numerical examples， and the influence of routing reliability level on the cost is analyzed. The experimental results show that the model can reasonably describe the problem， and the particle swarm optimization algorithm can effectively solve the problems of different sizes. With the increase of reliability level， the total cost increases， the setup cost has no obvious change， the vehicle operation cost increases， and the transportation and processing costs increase. This research is of great significance to improve the reliability of waste recycling system.

Key words： waste recycling; locationrouting; route reliability; particle swarm optimization