影响铸坯拉速的关键因素数值模拟研究
2021-08-19任劲宇王文豪姜芳芳娄一博
李 璐,任劲宇,王文豪,姜芳芳,娄一博
(中国重型机械研究院股份公司,陕西 西安 710032)
0 前言
棒线材免加热直接轧制技术(简称DROF[1])的大力推广应用,使提高铸坯拉速以尽可能提高入口轧制温度显得尤为关键。影响连铸坯温度提高的关键因素较多,如拉速、二冷区配水量、结晶器结构设计等,其中拉速对铸坯温度的影响尤为显著。相关学者对连铸段进行了大量研究[2-5],特别是结晶器改进方面取得了较好的成果,但由于很多研究均将热物性参数处理为常数[6],或设定边界条件时并未考虑角部热流量变化[7],或并未将整个连铸段综合考虑[8-9],所以建立的数学模型与实际应用偏差较大,从而影响研究铸坯温度的因素量化。
本文针对某钢厂120 t连铸段生产线,基于有限元软件ANSYS和材料性能软件Jmatpro,综合考虑了二冷区辊热问题以及结晶器角部热流量变化并动态采集了热物性参数,建立了小方坯在连铸段的温度场模型,定量分析了连铸段影响拉速的壳厚和二冷区配水量两大关键因素。将模拟所得数据与现场实际进行了对比,两者相对误差低于3%,验证了模拟的准确性,所得数据为提高连铸拉速提供了重要参考。
1 小方坯凝固传热模型的建立
小方坯凝固过程是一个随温度的降低而液态逐渐转变为固态的过程,如图1所示。由于内部温度高,凝固过程复杂,检测仪器难以观察,因此,对方坯的温度场及内坯壳形成进行有限元仿真,可清楚地分析随温度变化坯壳的形成、增加过程,便于准确地确定小方坯连铸工艺参数以及对产品质量的控制。
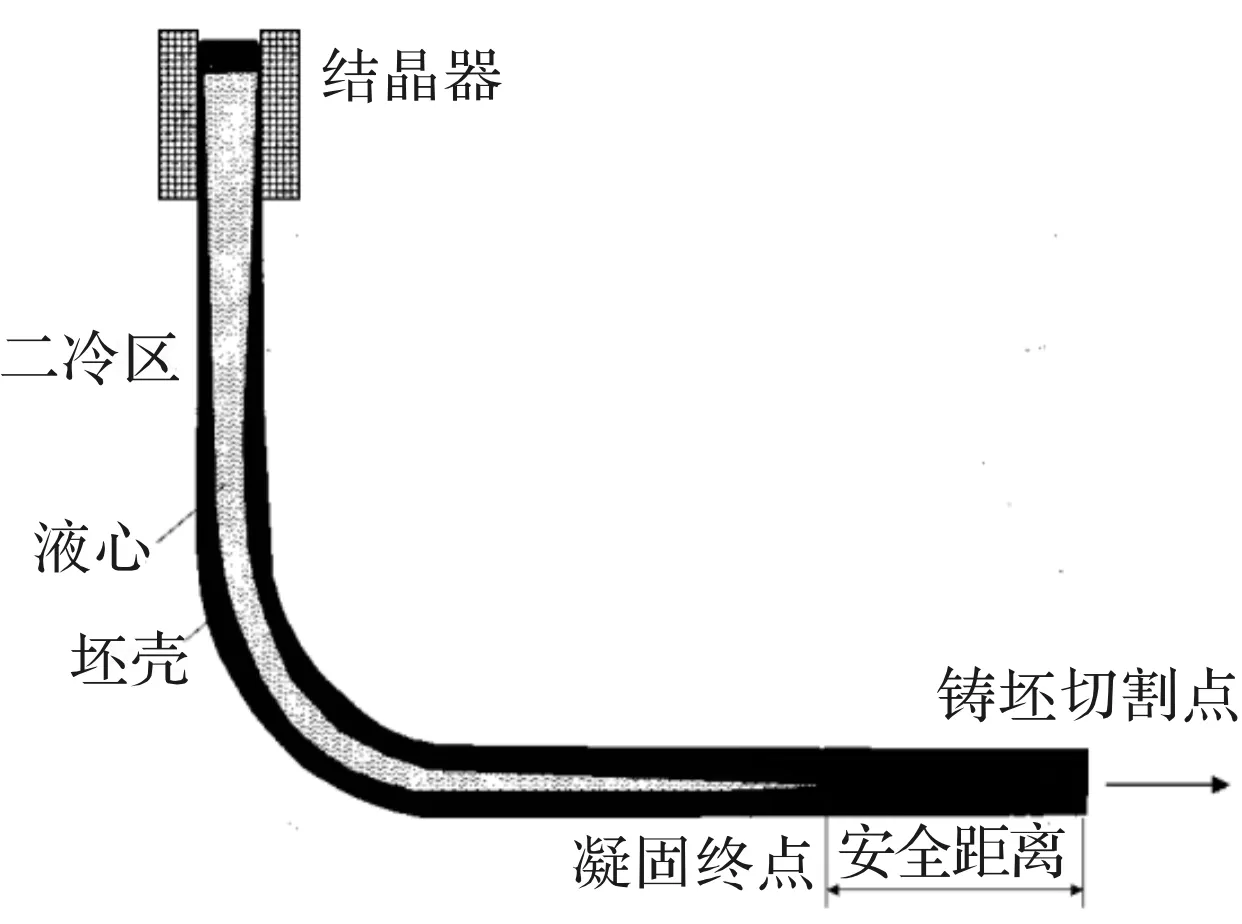
图1 凝固过程示意图
1.1 铸坯传热过程的计算假设
(1)忽略铸坯沿拉坯方向上的传热,将铸坯凝固传热过程视为二维瞬态传热问题且认为在垂直于拉坯方向的平面上,铸坯的传热是各向同性的。
(2)在整个凝固过程中钢水成分无变化,无偏析现象出现,也就是说在计算过程中,液相线温度和固相线温度始终不变,而在一个温度点上,物性参数恒定不变。
(3)不考虑凝固过程中钢坯整体收缩和内部钢水流动。
(4)忽略结晶器振动对铸坯凝固传热的影响。
1.2 传导方程及求解条件
在垂直于拉坯方向上取一铸坯薄片,如图2所示。并设定该薄片以拉坯速度向拉坯方向运动。以薄片中心为原点,分别以薄片相邻两边的方向为x轴、y轴,则铸坯薄片的傅里叶热传导微分方程为[7]
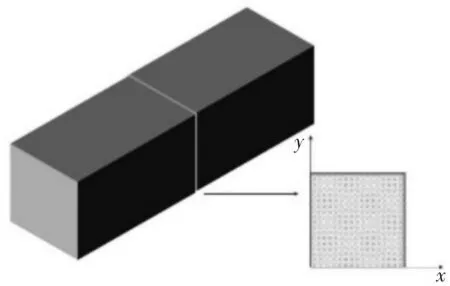
图2 薄片示意图
式中,T为温度,℃;t为时间,s;ρ为密度,kg/m3;c为比热容,J/(kg·K);λ为导热系数W/(m·K)。
(1)结晶器区边界条件[11]。
式中,q为边界上各节点沿边界法向的热流,W/m2;b为经验常数。
由于结晶器冷却不均和铸坯凝固收缩,结晶器和铸坯之间存在气隙,根据在横、纵两个方向上气隙大小的分布规律,本文对边界条件进行了修正,如图3所示。弯月面以下0~0.1 m处为紧密接触区,铸坯表面导出热流密度均为q;弯月面以下0.1~0.23 m处为气隙形成区,铸坯表面中心区域导出热流密度为q,角部导出热流密度为0.8q;弯月面以下0.23 m到结晶器底部为气隙稳定区,铸坯表面中心区域导出热流密度为q,角部导出热流密度为0.7q。
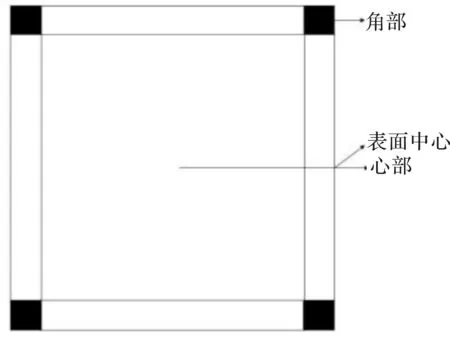
图3 边界条件修正示意图
(2)二冷区边界条件。
q=h(T-TW)
式中,T为铸坯表面温度,℃;TW为冷却水温度,℃;h为铸坯与冷却水之间的对流换热系数,W/(m2·K)。
对流换热系数h选用的对流换热公式[12]为
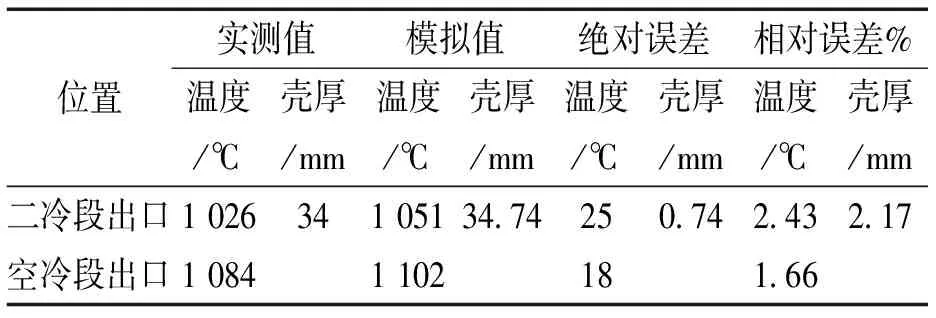
h=581ω0.451×(1-0.0075×ter)(1<ω<7,625 式中,ω为水流密度,L/(m2·s);Ter为二冷水温,℃。 (3)空冷区边界条件[13]。 式中,ε为黑度系数,本文取0.86;σ为斯特潘-玻尔兹曼常数5.67×10-8W/(m2·K4)。 使用ANSYS软件建立铸坯的二维模型,本文进行了温度场和应力场分析,且在温度场中考虑到铸坯与环境热辐射问题,故铸坯模型单元类型选择Plane55和surf151。 (1)热物性参数的处理。借鉴实验数据[14]及利用Jmatpro[15,16]来处理热物性参数。某钢厂连铸车间生产钢种为HRB400E/HRB500E。表1为其钢种成分表,图4为其热物性参数表。 表1 钢种成分表 % 图4 HRB400E各热物性参数图 (2)参数确定。弧形连铸机参数见表2。 表2 弧形连铸机参数 现场用热像仪对二冷区和空冷段出口附近铸坯的表面温度进行测量,用射枪法对二冷区出口坯壳厚度进行测定,用以验证模拟结果的可靠程度。温度及壳厚实测值与模拟计算值比较如表3所示,由表3可知铸坯表面温度与计算结果相对误差小于3%,绝对误差小于30℃;实际壳厚与计算结果相对误差小于3%,绝对误差小于2 mm,由此可知模拟结果可信度比较高。 表3 固、液相线温度 影响铸坯拉速的主要因素有坯壳厚度、二冷区各段水量及浇注温度等。一般情况下,浇注温度取决于钢的化学成分、炼钢工艺、浇注工艺等因素,可调整的范围很小。因此提高铸坯拉速要围绕坯壳厚度和二冷区各段水量来进行。 提高拉速可以减少铸坯在结晶器、二冷区及空冷区的冷却时间,必然会使铸坯温度提高。图5是拉速在2.30 m/min时各出口的温度云图,图6为在冷却条件不变的情况下,拉速对铸坯在结晶器、二冷区及空冷区出口处表面温度的影响。 图5 拉速为2.30 m/min时各出口温度云图 图6 拉速不同时各出口温度变化图 可以看出,铸坯拉速在2.3~2.6 m/min范围内时,铸坯在三个区域与拉速几乎呈线性关系。铸坯拉速在2.3 m/min时,结晶器、二冷区、空冷区等出口的铸坯温度分别为1 031.07 ℃、1 050.12 ℃、1 100.79 ℃。铸坯拉速在2.6 m/min时,结晶器、二冷区、空冷区等出口的铸坯温度分别为1 077.45 ℃、1 066.82 ℃、1 130.24 ℃。结合曲线图可知,相当于拉速每提高0.1 m/min,在各段出口温度均有所提升:结晶器出口可提升约17℃;二冷区出口可提升8.5℃左右;空冷区出口可提升约18℃。 由图7可知,随着拉速增大,结晶器和二冷区出口处的坯壳有所减薄:拉速每增加0.1 m/min,结晶器出口处坯壳厚度减少约0.26~0.56 mm二冷区出口处坯壳厚度减少约1.45 mm。同时,随着拉速的增大,铸坯在空冷区同一位置的凝固程度明显不同,拉速改变后同一位置凝固如图8所示。相当于拉速每增加0.1 m/min,而液芯长度要增加0.56 m。由此可知,主要限制拉速提高的不是结晶器出口的坯壳厚度,而是铸坯的液芯长度。如需提高拉速,必须使得凝固终点前移,保证足够的安全距离(一般需大于0.5 m),可通过增大铸机半径,优化结晶器与二冷区的冷却工艺制度等。 图7 拉速改变后各出口壳厚及凝固终点变化 图8 拉速改变后同一位置凝固图 由图9可知,每增加20 %的结晶器配水量,结晶器出口处壳厚增加2.27 mm,凝固终点(液芯长度)缩小0.77 m。所以,当适当增强结晶器冷却能力,结晶器出口坯壳厚度大幅度增加并在切割点前能保证足够的安全距离,为提高拉速创造了条件。 图9 拉速为2.3 m/min时,壳厚及凝固终点随结晶器配水量变化 从图10可知,在拉速为2.30 m/min且其余条件均不变的情况下,当提高二冷区某段冷却强度时,其余阶段均未发生显著变化(其温差小于1℃);当改变整体二冷区配水强度时,冷却强度增大,铸坯的表面温度降低,冷却强度增加20%,铸坯的表面温度在空冷区出口处降低约27.5 ℃。因此,要实现满足DROF工艺的目标表面温度就要对整个二冷区的配水进行综合考虑,只对其中某一段进行改变的方案,并不能达到理想效果。 图10 改变二冷区各段及整体配水表面中心温度变化图 由图11可知,在二冷区出口处,当增大足辊段配水量20 %时,壳厚增大约0.2 mm,液芯长度缩小0.066 m;当增大二冷一段配水量20 %时,壳厚增大约0.8 mm,液芯长度缩小0.249 m;每增大二冷二段配水量20 %时,壳厚增大约0.3 mm,液芯长度缩小0.062 m;当使整体二冷区配水量增大20 %时,壳厚增大约1.3 mm,液芯长度缩小0.320 m。 图11 改变二冷各段配水量二冷区出口壳厚及凝固终点的变化 在足辊段,连铸坯壳形成较薄,铸坯温度较高,使得芯部液相区占比大,所以应该提高该段冷却强度,促使坯壳迅速生长,以保证不发生漏钢。在二冷区一、二段,铸坯已形成较厚的凝固坯壳,凝固坯壳热阻较大,此时应适当减小冷却强度,来获得较高的铸坯温度,便于进行直接轧制。与此同时,也可避免因为冷却强度过高所造成铸坯表面热应力过大而产生裂纹,影响铸坯质量。 本文基于某钢厂DROF小方坯连铸生产现状,利用软件ANSYS和JMatpro建立了小方坯连铸过程中的温度场模型,定量分析了连铸操作工艺对提高拉速的影响。 (1)拉速每提高0.1 m/min,在空冷区出口,铸坯表面温度可提升约18 ℃。主要限制拉速提高的不是结晶器出口的坯壳厚度,而是铸坯的液芯长度。如需提高拉速来实现铸坯提温,必须使得凝固终点前移,保证足够的安全距离(一般需大于0.5 m),可通过提高铸机半径,优化结晶器与二冷区的冷却工艺制度等。 (2)二冷区整体配水量增加20%,铸坯的表面温度在空冷区出口处增加约27.5 ℃,液芯长度缩小0.32 m,使拉速提高的成为可能。通过调整二冷区的配水来控制铸坯的表面温度,要对二冷区各段的水量进行整体的调整,单纯改变某一段的水量,不能达到预期效果。同时,应在足辊段提高冷却强度,促使坯壳迅速生长,在二冷其余阶段,减小冷却强度,来获得较高的铸坯温度。1.3 有限元模型的建立



1.4 实测值与模拟值的比较分析
2 模型计算结果
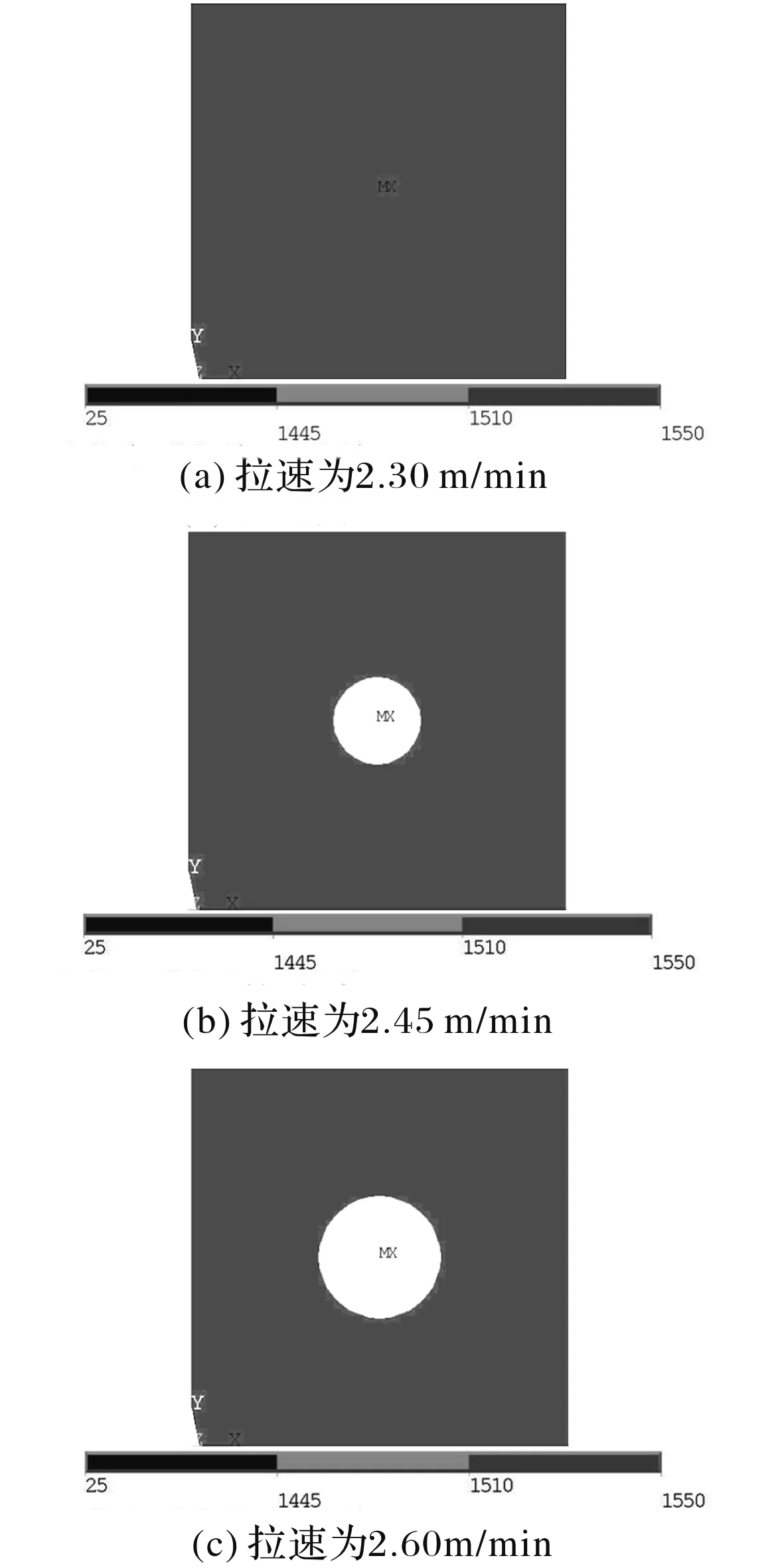
2.1 铸坯温度与铸坯拉速的关系


2.2 坯壳厚度与铸坯拉速的关系



2.3 二冷区各段冷却强度与铸坯拉速的关系


3 结论
