基于Ansys的穿孔铝板有限元分析
2021-08-19马振国曹亚军高勇勇
马振国 黄 冬 姚 琼 曹亚军 高勇勇
1. 西安丝路国际会展中心有限公司 陕西 西安 710000;
2. 中建深圳装饰有限公司 广东 深圳 518035
板壳结构广泛应用于现代工程结构中。穿孔铝板因其穿孔的特性可以在外界和建筑内部之间形成通透的界面,既可以展现建筑的整体效果,又可以维护室内空间的私密性,此外还具有采光和遮阳功能。在目前接触到的项目中,穿孔铝板的运用越来越广泛。
板壳结构在大多数应用场合中主要受弯曲作用,因此其承载能力与弯曲刚度和强度息息相关。决定板壳抗弯性能的主要因素是材料的力学性能与结构的几何形状[1],而对于相同材料和特定几何形状的均匀多孔板壳来说,穿孔率对其弯曲刚度和强度的影响很大。
大挠度穿孔板的计算是非常复杂的非线性弹性力学问题,难以用简单公式计算,而要用到专门的计算方法和软件,对具体问题进行具体计算,显然这对于幕墙设计是不适用的[2]。然而按照实际穿孔情况进行有限元建模分析,需花费较多时间,且当板块尺寸过大时,会产生过多的单元数量,易出现软件内存不足而无法计算的情况。对于多孔的板壳结构,由于存在着孔之间的相互影响,故应力分析较复杂,采用归纳的拟合计算式求解是一个较好的选择。为提高计算效率,简化穿孔铝板的计算[3],本文以均布荷载作用下的均匀穿孔铝板为对象,通过有限元分析得出穿孔形状、穿孔率、板厚、尺寸规格、风压大小与穿孔铝板最大变形及应力间的关系,并归纳出相关的拟合计算式。
1 穿孔形状对穿孔铝板最大变形和应力的影响分析
本节分别对50%穿孔率,板块尺寸1 000 mm×1 000 mm,板厚3 mm,风压1.0 kPa情况下的菱形孔、圆孔、方孔和六边形孔的穿孔铝板进行有限元计算,分析了穿孔形状对其最大变形和应力的影响(图1)。
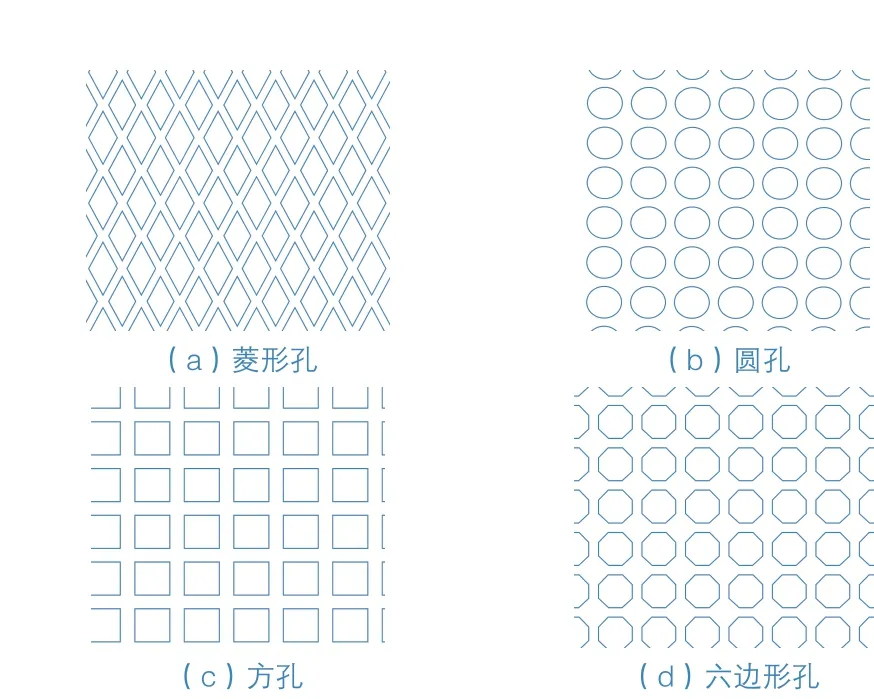
图1 各种铝板的穿孔形式
本文采用Ansys有限元分析软件建立计算模型,穿孔铝板采用三维壳单元(SHELL63),该单元为4节点,可定义厚度,约束条件为四边简支。当板的挠度大于板厚时,应按规定考虑大挠度的影响。考虑大挠度板的计算是非线性弹性力学问题,线性叠加原理不再适用,因此将Ansys的NLGEOM项设置为ON。对模型进行单元网格划分后,计算求解得到不同穿孔形状铝板的位移与应力云图,如图2~图5所示。

图2 菱形孔穿孔铝板的位移与应力云图

图3 圆孔穿孔铝板的位移与应力云图
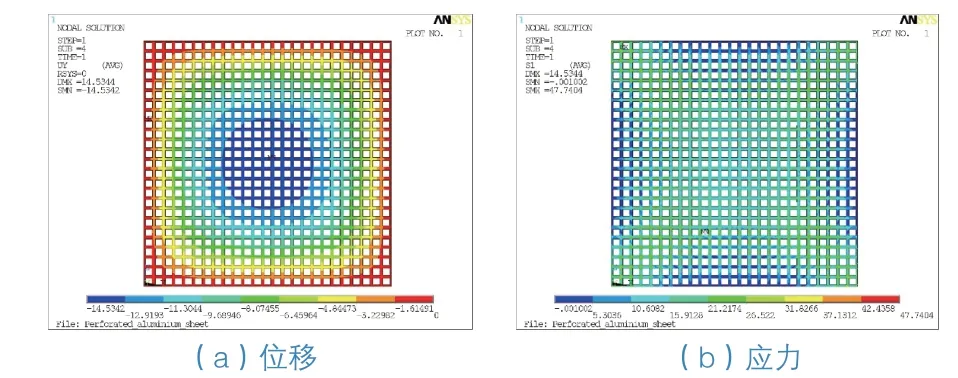
图4 方孔穿孔铝板的位移与应力云图

图5 六边形孔穿孔铝板的位移与应力云图
无论是菱形孔、圆孔、方孔还是六边形孔,在其他因素相同的情况下,最大位移和应力基本一致,穿孔形状对穿孔铝板的最大位移和应力无太大影响,如表1所示。

表1 穿孔形状的影响
2 穿孔率对穿孔铝板最大变形和应力的影响分析
为分析穿孔率对穿孔铝板最大变形和应力的影响,在建模分析过程中,每种工况除了穿孔率(从0~75%)一个变量外,其他条件保持一致。分别计算了3种工况:
1)板块尺寸1 000 mm×1 000 mm,板厚3 mm,均布风压1.0 kPa,穿孔形状为圆孔。
2)板块尺寸1 000 mm×1 000 mm,板厚6 mm,均布风压1.0 kPa,穿孔形状为圆孔。
3)板块尺寸1 000 mm×1 000 mm,板厚3 mm,均布风压1.5 kPa,穿孔形状为圆孔。
为便于分析穿孔率对穿孔铝板最大变形和应力的影响,将不同穿孔率铝板最大变形与未穿孔铝板最大变形相比,得到挠度比;将不同穿孔率铝板最大应力与未穿孔铝板最大应力相比,得到应力比。未穿孔铝板位移与应力云图如图6所示,3种工况下穿孔率对应力比、挠度比的影响曲线如图7所示。
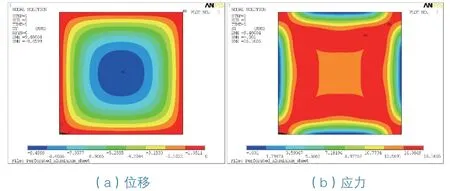
图6 未穿孔铝板的位移与应力云图

图7 3种工况下穿孔率对应力比、挠度比的影响
在图7中,红色曲线、蓝色曲线、绿色曲线分别为工况一、工况二、工况三条件下穿孔率对应力比、挠度比的影响曲线。
计算结果表明:不同板厚、板块尺寸、风压条件下,穿孔率对应力比、挠度比的影响趋势具有一致性。在10%~50%穿孔率范围内,应力比变化不大,在其他条件保持一致的情况下,穿孔铝板最大应力是未穿孔铝板最大应力的2.5倍。在穿孔率不高于50%的情况下,挠度比与穿孔率呈一次函数关系。当穿孔率达到60%后,应力比和挠度比急剧增大。考虑工程经济及安全性,穿孔铝板穿孔率宜控制在60%以下。
3 数据拟合
由图7可知,不同工况条件下的应力比、挠度比随着穿孔率增大具有相同的变化趋势。采用多项式逼近,利用Matlab曲线拟合工具箱对多组工况下穿孔率对应力比、挠度比的影响曲线进行数据拟合,得到了相关拟合计算式。
由拟合结果可知,应力比与穿孔率之间的关系采用多项式逼近的拟合计算式。误差平方和为0.272 4,确定系数为0.990 8,非常接近1,表明方程的变量对应力比的解释能力非常强,计算式对数据拟合得比较好。
由挠度比与穿孔率的关系拟合结果可知,挠度比与穿孔率之间的关系采用多项式逼近的拟合计算式,误差平方和为0.062 1,确定系数为0.966 9,非常接近1,表明方程的变量对挠度比的解释能力很强,计算式对数据拟合得比较好。
4 算例
为便于工程中实际应用,基于拟合计算式给出了不同穿孔率下穿孔铝板与未穿孔铝板之间的应力比和挠度比,如表2所示。

表2 不同穿孔率下的应力比和挠度比
以板块尺寸1 000 mm×480 mm、板厚3 mm、风压1.5 kPa为例,通过Ansys有限元分析,未穿孔铝板最大应力为21.68 MPa,最大变形为4.25 mm。由表2可知,在50%穿孔率条件下,穿孔铝板与未穿孔铝板之间的应力比为2.51,挠度比为1.39。由此知,50%穿孔率穿孔铝板最大应力为21.68×2.51=54.42 MPa,最大变形为4.25×1.39=5.91 mm。根据Ansys有限元分析,50%穿孔率的铝板最大应力为48.44 MPa,最大变形为6.21 mm。相比有限元计算结果,拟合计算式结果存在偏差,最大应力偏差比为12.3%,最大变形偏差比为4.8%。根据DG/TJ 08-56—2019《上海市建筑幕墙工程技术标准》[4]可知,若铝板材质为3003-H14,则强度限值为97 MPa,挠度限值为480/60=8 mm,强度利用率达到50%,挠度利用率达到78%。由此可知,该穿孔铝板变形起控制作用。在变形起控制作用的前提下,拟合计算式结果偏差比为4.8%,具有较高精确度,基本满足工程计算要求。
5 结语
通过不同工况下穿孔铝板的数值分析,可以得出以下结论:
1)对于相同材料和特定几何形状的均匀多孔板壳,穿孔形状对其弯曲刚度和强度影响不大。
2)不同工况条件下,应力比、挠度比随着穿孔率增大具有相似的规律,可以用拟合计算式表达。
3)在弯曲刚度起控制作用的情况下,拟合计算式具有较高精确度,可为后续工程提供借鉴。
利用所拟合的计算式,能够简化穿孔铝板计算,提高效率,具有较大的实用意义。穿孔铝板在大多数应用场合中是均匀穿孔矩形板,因此本文仅对此进行了研究。此外,板型和非均匀穿孔情况下的穿孔位置对穿孔铝板的承载能力也有影响,可作进一步研究。
