提升思维品质 促进学生数学核心素养
2021-08-19程兰花
程兰花
(江苏省泰州市姜堰区第四中学 225500)
将数学教学与素养发展融为一体,就需要教师不断地提升学生的思维能力.具体来说,需要培养学生预习的习惯,以让他们发现问题;需要培养他们合作的习惯以让思考深入;需要补给他们的短板以让思维点燃;需要着眼发展以让思维优化.
一、自主开展预习,发现问题
教与学的不相通往往体现在教师讲的学生会,学生不会的教师讲不到.要改变这种教与学不联通的现象,最好先让学生预习,让他们去发现问题,进而教师在讲解的时候就能抓住重点,各个突破.当前在数学教学上,预习是一个薄弱的环节,有些寄宿制学校甚至取消预习,将所有的时间都划分给不同的学科,以让教师有足够讲解的时间.其实教师要利用好预习这个环节,让学生学会发现问题,以引发思维.
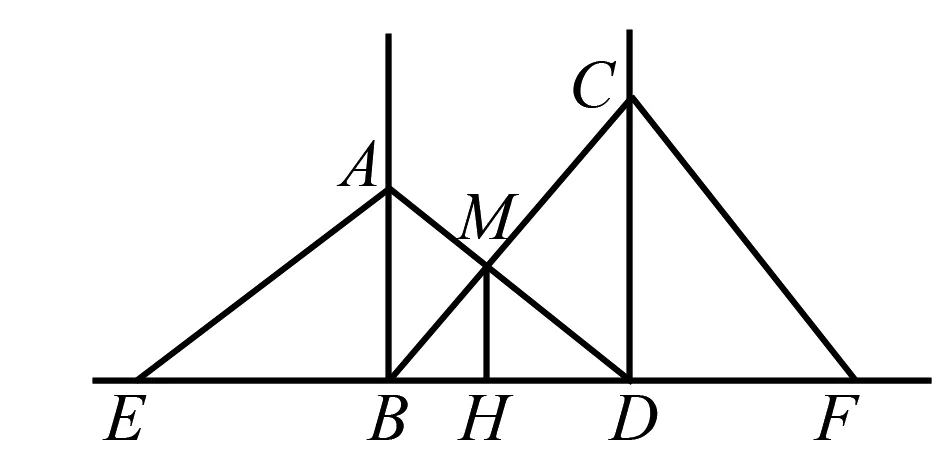
图1
以人教版新教材《相似三角形应用举例》为例,教师设置这样的预习题:工地上两根电灯杆相距L米,分别在高为4米、6米的A、C处用铁丝将两杆固定,求铁丝AD与铁丝BC的交点M处离地面的高MH.教师设置题目的目的,就是想让学生将上一节学到的有关相似三角形的性质运用起来.学生也知道教师的这一目的,因此他们在将题目画成如图一所示的图形之后,就提出这样的问题.这图中有几个相似三角形,能不能将他们找出来.在找出相似三角形之后能不能运用其性质,将实际问题解决.学生在画完图之后,根据题目的意思,发现两组相似三角形△BMH∽△BCD,△DMH∽△DAB,但是部分学生的思考几乎卡壳了,他们不能进一步拓展思维,换言之,他们不能将题目中的,“工地上两根电灯杆相距L米,分别在高为4米、6米的A、C处用铁丝将两杆固定”,这些条件运用起来.教师看重的不是预习的结果,而是他们在预习中的思考.当学生将这样的问题呈现出来,教师就知道他们进行了哪些思考,还需要在哪些方面做些努力.一次成功的预习,就是能让学生发现新的问题,进而引发思维持续参与.
二、小组交流学习,促进思维
学生先学的方式也是多种多样的,进行小组合作就是一种有效的方式,小组合作能将发现的问题不断深化下去,进而让更深入的思考成为可能.小组合作还是以学生学为主,只是他们由单一的思维,变成一起思维,他们由发现问题,到向别人学习解决问题的方式.可见小组合作学习让思考变得有效.
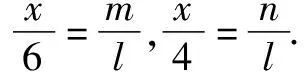
三、补给个性需要,点燃思维
在合作之后,教师要关注的就是如何调整教学目标,即通过一堂课的教学要解决学生合作中的哪些问题,个别学生在理解与运用上要达到怎样的一个程度.这个目标的制定不是凭空而来的,是依据学生的合作而来的.教师要从学生的合作中看到学生需求,进而才能调整目标,也就是说,教师的教学目标要与学生的需要对接.比如说,学生需要的是如何理解基本的概念,作为教师在教学的时候就要围绕这样的主题展开思维训练.
以下面这题为例,已知某商品的进价为每件40元,售价是每件60元,每星期可卖出300件.市场调查反映:如果调整价格,每涨价1元,每星期要少卖出10件.要想获得6000元的利润,该商品应定价为多少元.教师是这样预设的:先让学生设涨价x元,则每件的利润为(60-40)+x=20+x,每星期销售的件数为300-10x,设获得利润为y,根据题意,得y=(20+x)(300-10x),获得利润为6000,则(20+x)(300-10x)=6000,解得x1=0,x2=10.因此,当售价定位60元或70元,都能获得6000元的利润.但学生在合作的过程中出现这样的问题,一是学生能列出方程式,但是方程解不出来,换言之,他们对二次方程的解法还需要一定的训练,需要将基本的计算做进一步的强化.同时他们解出答案之后,不会将设置的未知数换成问题中的数据,即不能将方程与实际的运用对接起来.基于学生这样的现状,教师可以理解为学生需要的是解方程的能力,以及对相关的结论分类讨论的能力.因此教师在教学的时候就需要关注学生解方程的过程,不能一笔带过,要看看他们每一步的变式是不是合理的,准确的.因此在教学的过程中,教师需要研究学生,研究他们合作的过程中存在的一些具体的问题,进而打开他们认知与情感的窗口,更好地与他们对话.
四、着眼学生发展,优化思维
当学生能解答出一元二次方程之后,当他们对如何运用方程解决实际问题已经有一定经验之后,教师就要着眼于学生的发展,进一步拓展他们的能力,围绕着这样的题目,让学生朝着一定的深度去思考.换言之,教师设定的题目还要与这个有关,但是相应的难度要大些.难度大一些,无非就是题目的情境换了,相关的条件做了一些变化.教师这样地选举教学内容,主要是检测教师教的情况,以及学生对其掌握的情况.教师设置的题目为:已知某商品的进价为每件40元.现在的售价是每件60元,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.如何定价才能使利润最大.跟原来的题目相比,涉及到的条件明显多了,学生看到的数据也多了.但是在做第一道题目的时候,学生已经明白了题目中相关的数与量的关系,即,售价=进价+进价×利润率;利润率=(售价-进价)÷进价;定价=标价;进价=售价÷(1+利润率);利润=售价-进价(成本价);利润率=(利润÷成本)×100%;获利款=售价额﹣进价额.对着这样的公式,学生设涨价x元,则每件的利润为(60-40)+x=20+x,每星期销售的件数为300-10x,设获得利润为y,根据题意,他们得到这样的方程式:y=(20+x)(300-10x),y=-10(x-5)2+6250;所以当涨价时,涨价5元,也就是定价为65元时,最大利润为6250元.大多学生做到这儿就以为结束.教师的教就体现在所选择的内容能拓展学生的能力.因此教师问,涨价会获得利润,那么降价会遇到怎样的情况.教师的教就在于点拨,就在于给学生以思路.简单的提醒,学生就想到,如果降价时,就设降价x元,那么每件的利润为(60-40)-x=20-x,每星期销售的件数为300+20x,设获得利润为y,根据题意,能得到这样的方程式:y=(20-x)(300+20x),y=-20(x-2.5)2+6125.不要计算,学生也能发现不管怎样,最大利润不会超过6125元.两次分类讨论相结合,学生发现当定价为65元时,才能使利润最大,最大利润为6250元.显然教师要能让学生有新的思考的空间,要能充分展示学生的多元智能.
提升学生的思维品质改变了原先的教学模式,极大地提升了教师与学生的主动性与创造性.因此教学中教师要不断探索新的教学模式,以尽可能地激发学生的思维火花,在引发他们多维度思考的同时,提升学生的核心素养.
