非金属柔性立管在海洋潮流下的动力响应特性研究

姜 振，赵 林

（中国海洋大学 工程学院，山东 青岛 266100）

海洋立管是连接顶部浮式平台和海底设施的海洋工程装备，在海洋油气资源开采中具有重要作用。柔性立管由于其多层复合材料和金属材料螺旋缠绕构成的结构特性，在保证展向抗拉能力的同时，其弯曲性能、抗疲劳和耐腐蚀等特性远优于刚性立管[1]，能够更好地适用于恶劣海洋环境，因此近些年来得到广泛应用。其中非金属柔性立管作为一种典型的粘结性柔性管，基于热粘合缠绕工艺使得内部各层之间相互粘结固定，能够避免出现非粘结性柔性管的层间滑移现象，因此往往具有更好的耐疲劳性能。在潮流作用下，立管两侧将会形成交替脱落的漩涡，从而引起立管上产生周期性脉动拖曳力和升力，导致立管在顺流向（In-line，IL）及横流向（Cross-flow, CF）上产生周期性振动，这种现象称为涡激振动（Vortex-Induced Vibration，VIV）[2]。当漩涡脱落频率接近立管的自振频率时将会发生“锁定”现象，加剧立管的疲劳破坏。

由于自然海况的复杂性，柔性立管涡激振动的动力响应问题一直是海洋工程领域研究的热点，众多学者对其进行了大量的模型试验以及数值分析工作。数值模拟多结合计算流体力学（Computational Fluid Dynamics, CFD）[3-4]以及经验模型方法[5-8]。模型试验作为验证研究和探索立管VIV响应规律的重要手段，能够与数值模拟结果相互印证从而提高预测VIV的准确性。但受成本和环境条件的限制，目前国内外模型试验工作主要集中于室内大比尺模型试验[9-12]，通过相似模型验证原型，但比尺试验往往难以同时满足长细比L/D和雷诺数Re的相似律，因此将现场模型试验的测试数据作为输入参量进行数值分析工作，以研究柔性立管的结构响应及振动规律，不失为一种可靠的研究手段。

本文以“863海洋深水非金属复合管研制项目”的海上模型试验数据作为环境参量，根据现场布设形式及顶张力监测数据调整立管静态平衡构型，采用水动力软件OrcaFlex[13]对非金属柔性立管进行数值模拟，研究海洋潮流作用下，流速和流向的改变对非金属柔性立管的力学性能和结构响应规律的影响，旨在为海洋柔性立管设计和海洋工程提供参考。

1 理论基础

悬链线式柔性立管在海洋环境荷载作用下的时域动力响应变量较为复杂，采用集中质量法和弹簧模型可以很好地对立管进行简化[14]，将立管分为若干连续的线单元和单元节点，线单元用来模拟立管轴向、弯曲和扭转特性，其他特性如质量、重力和浮力集中在节点上，并在计算中引入阻尼系数以考虑结构的阻尼特性，见图1。

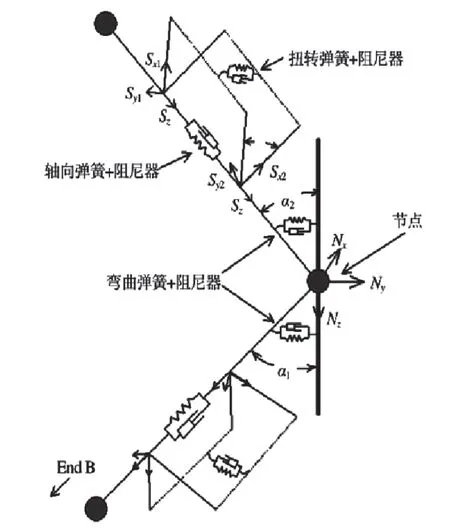
图1 OrcaFlex集中质量模型

这里仍采用经典的时域动力分析理论进行计算和模拟。该结构模型的动力控制方程如下：

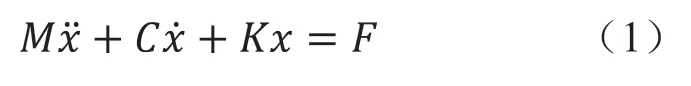
式中：M、C、K分别为结构质量矩阵、结构阻尼矩阵和结构刚度矩阵，它们由每个单位矩阵向量组成；F为管线所受外力，包括重力、浮力、拖曳力和惯性力等；x、x˙、x··分别为系统节点的位移、速度和加速度。

OrcaFlex中有效张力的表达式为：

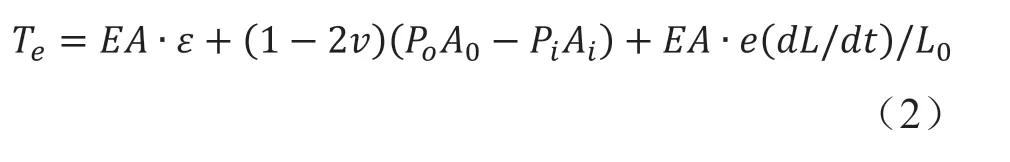
式中：Te为有效张力；EA为轴向刚度；ε为总的轴向平均应变，ε=(L-λL0)(λL0)，其中λ为分段的伸长系数；L0为分段的初始长度；v为泊松比；Pi和P0分别为内外压力；Ai和A0分别为内外截面积；e为阻尼系数；dL/dt为长度变化率。

由于柔性立管的动态特性是几何非线性的，因此常用时域分析方法。尾流振子模型是HARRTLEN[15]等根据大量实验数据建立的关于弹性支撑柱体涡激振动的横流向振动响应及流体力的经验模型。尾流振子是一个抽象概念，用来表征漩涡交替脱落形态的尾迹特征，一般用隐含流场变量表示。其中Milan和Iwan and Blevins两类尾流振子模型由于其较为明确合理的物理意义及良好的计算精度，被广泛应用于涡激振动时域分析软件中。以Van der Pol方程表达涡尾流振子的基本方程为[16]：

式中：q为流体振子无量纲变量；ε为Van der Pol参数，根据试验确定；f为无量纲振子受力；wf为来流作用下静止圆柱的漩涡脱落频率。在经验模型的选择上，本文选用了基于尾流振子模型的Milan Wake Oscillator（MWO）模型，在匀速流场中，使用Milan尾流振子模型对立管进行时域分析能够保证良好的计算精度，满足工程需要。

2 数值模型

为保证合理的数值计算结果，采用海上模型试验的立管拉力监测数据和布设方案对模型输入参量进行校准。文中海上模型试验在中国黄海海域（36°39.838´N，122°18.789´E）进行，海域水深为25.8 m，针对项目所研制的非金属柔性立管，通过拉力计、压力采集仪、信号采集仪、水下摄像机等设备对管道加压状态下的拉力、压力数据和运动信号进行了监测，对其安装操作性能、工作性能、结构安全和完整性、整体设计的可靠性等方面进行了试验检验。需要说明的是，由于海上模型试验中立管受铺管船平台运动、不规则波浪和海流联合作用，振动轨迹和VIV响应杂乱且不稳定，难以与模型计算结果进行比对，因此需要简化工况，以研究非金属柔性立管的动力响应规律。

基于上述计算理论，使用OrcaFlex软件建立非金属柔性立管的有限元模型，对该立管进行了时域动态分析，模型由非金属柔性管道、弯曲加劲肋和铺管船等组成。立管布置形式与空间位置与海上模型试验保持一致，立管上端部分通过弯曲加劲肋刚性悬挂在船体上，悬挂角为10°，目的是约束柔性立管从而避免过度弯曲以及高循环疲劳损伤的累积，立管顶端距水面4 m，横跨段为21 m，下半部分平铺于海床上，呈悬链线姿态，见图2。立管末端锚固在海床上，立管整体无扭转，船体垂直于潮流流向和柔性立管铺设方向。试验中采用的非金属柔性立管模型全长为100 m，外径为223 mm，内径为150 mm。非金属柔性立管截面见图3，模型参数见表1。本研究中忽略弯曲加劲肋与柔性管之间的径向间隙和摩擦力的影响，表2给出弯曲加劲肋的几何尺寸。柔性立管与海底的相互作用采用线性假设，其他参数均为软件默认。

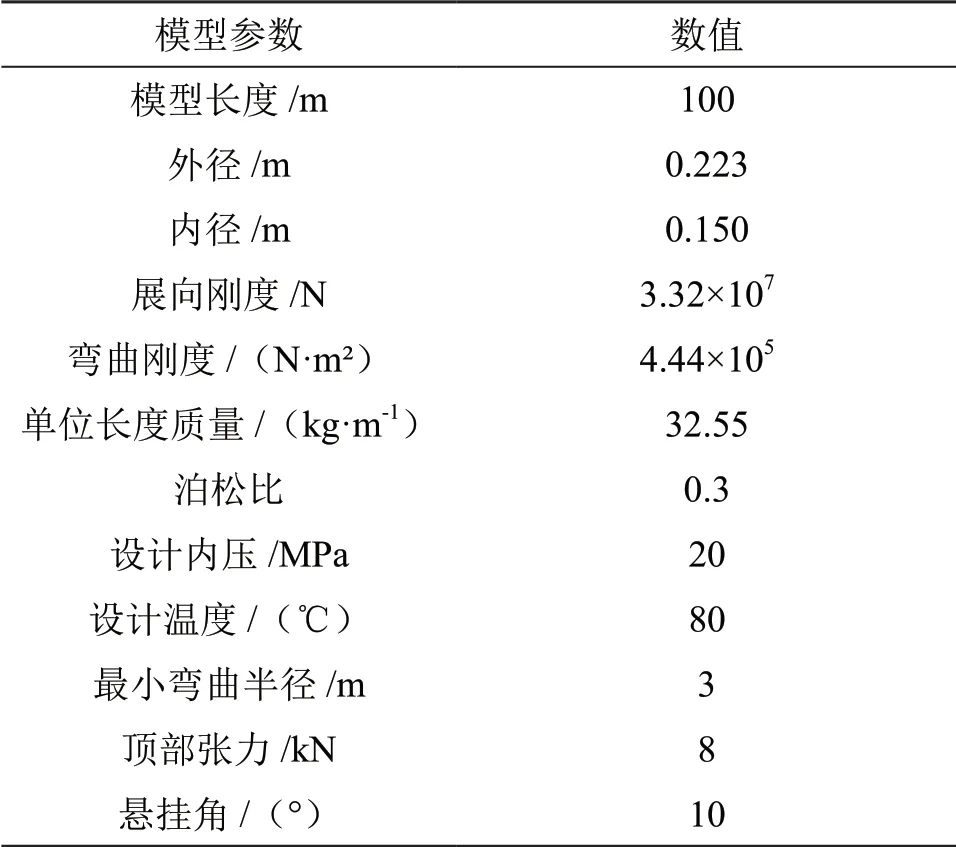
表1 柔性管模型参数

表2 弯曲加劲肋的几何参数

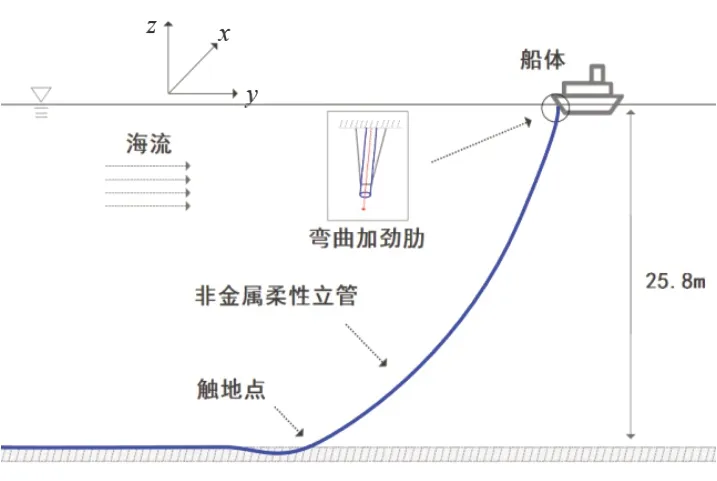
图2 悬链线柔性立管的整体分析模型

图3 软管截面

本研究不考虑上部浮体运动和波浪的影响，重点研究均匀流条件下，潮流流速和流向的改变对悬链线式非金属柔性立管动力响应特性的影响。这里假定图2模型中海流自左向右传播，称为正向流，反之称为反向流。选取的工况为正反流向时，潮流平均流速分别取0.2 m/s、0.4 m/s、0.6 m/s、0.7 m/s、0.8 m/s、1.0 m/s和1.2 m/s。

3 结果分析与讨论

3.1 立管张力及固有频率分析

立管轴向应力是评估管线结构安全的重要指标，同时能够影响管线的振动特性。图4为立管在不同潮流流向，0～1.2 m/s流速条件下的顶部有效张力平均值，从图中可以看出立管在正向流时顶张力随流速变化逐渐增大，但在反向流时随流速增大顶张力迅速减小。这是由于模型中悬链线立管模型柔性大抗弯刚度小，作用在立管迎流面的流体力除了少部分转换成立管横截面剪切力外，大部分转换成沿立管展向的应力。而反向流时由于流体与立管剪切角的变化，流体力沿立管轴向补偿了部分应力，使得立管顶部张力逐渐较小。通过时域分析得到200 s内立管轴向张力的统计分布曲线，如图5所示。由于在均匀流场中立管受海流荷载作用形成稳态振动，因此统计的最大值、最小值和平均值较为接近。可以看到立管轴向张力沿着弧长方向不断减小，由于弯曲加劲肋的约束，有效张力在立管顶部下降较快，而在触地点附近变化缓慢。

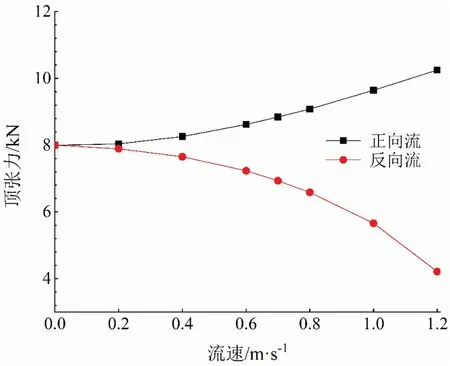
图4 立管顶张力随流速变化

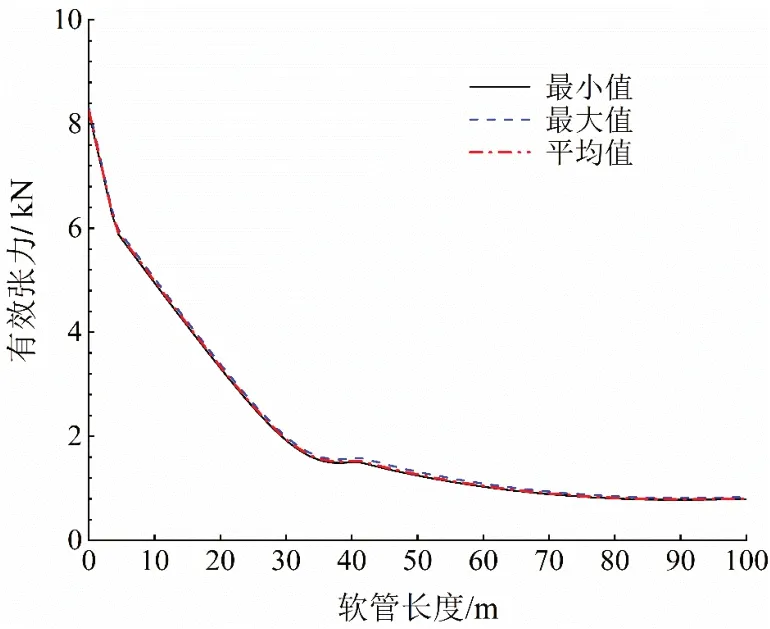
图5 立管张力沿管线分布

使用有限元对立管进行模态分析，并计算8 kN顶张力作用下立管的前10阶固有频率，结果如表3。利用OrcaFlex得到对应的前4阶水下立管模态，如图6（a）至图6（d）所示，可知在单一振型下立管悬垂段轴向上的振动幅值大致相同。

表3 立管固有频率计算结果

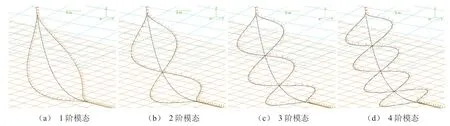
图6 水下柔性立管振动模态

3.2 立管模型VIV响应特性分析

柔性立管在来流时，当漩涡脱落频率接近立管固有频率时，可能会发生“锁定”现象。图7为正向流时，流速0.4 m/s下柔性立管在展向L=20 m处CF方向与IL方向上的VIV位移时历曲线和频谱分析结果。可以看到：均匀流条件下，柔性立管在CF和IL方向的VIV为单一频率下的稳态振动，且CF方向的振动幅值较IL方向要大一个数量级。而在频率方面，由频谱图可以看出，立管IL方向的振动频率是CF方向振动频率的2倍，表明此时存在稳定的涡激振动现象。

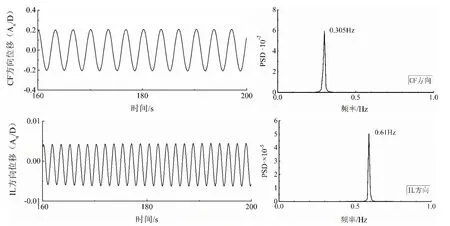
图7 0.4 m/s流速下立管在L= 20 m处位移时历和频谱图

无因次振幅比（A/D）是评价立管涡激振动响应的主要参数之一，其中A为立管振幅，D为立管模型直径。图8和图9统计了正向流和反向流条件下，柔性立管展向上CF方向的VIV最大响应位移随流速变化的关系曲线。

从图8可以看到，在正向流作用下，柔性立管展向最大响应位移随着潮流流速增加而增加，在流速U为0.7 m/s时达到最大值为0.33D，此时立管主导频率为0.475 1 Hz，接近4阶模态。随着流速继续增加，VIV最大响应位移迅速下降，在1.2 m/s时逐渐稳定，此时位移为0.02D。另一方面，由图9可以看到，不同于正向流条件下的表现，立管在反向流作用下，CF方向的最大响应位移与流速U（0.2～0.8 m/s）呈正相关，在0.8 m/s时达到峰值为0.58D，在1.0 m/s时回落到0.51D，而在1.2 m/s时达到最大值为0.64D，此时立管主导频率为0.760 2 Hz，接近5阶模态。

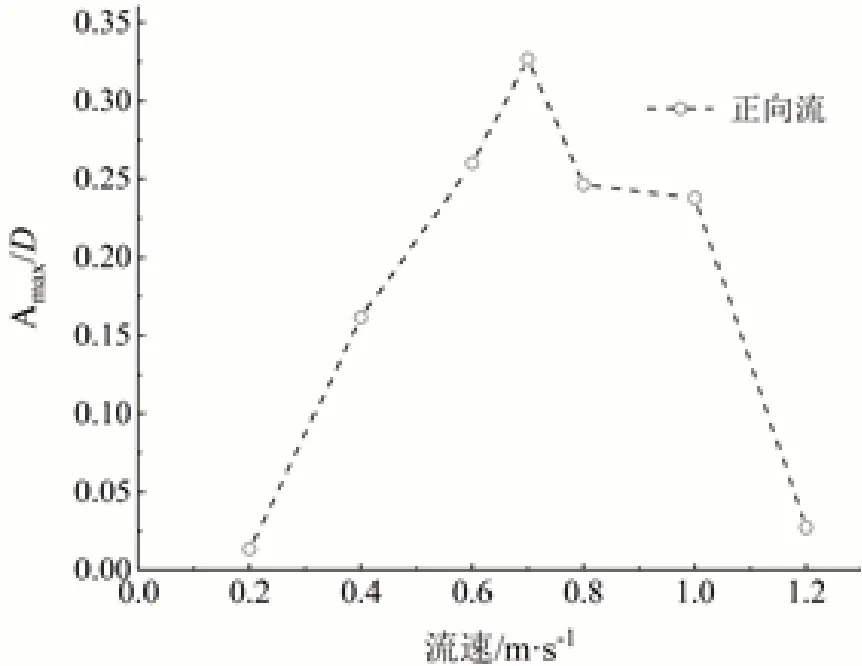
图8 正向流立管最大振幅A/D随流速变化

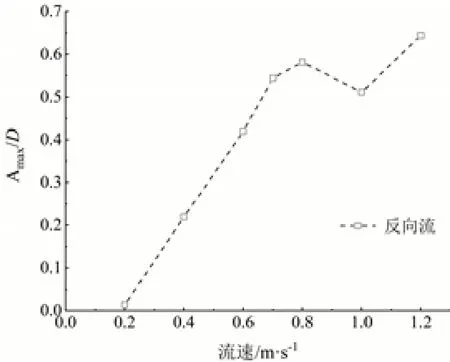
图9 反向流立管最大振幅A/D随流速变化

由此可见，潮流流速不仅会影响立管的振动模态，流向的改变还会影响立管的VIV响应幅值，这是由立管的柔性结构决定的。非金属立管结构的柔性大，自然模态的频率低且相邻模态的频率差值小，这使得柔性立管很容易被激发高阶模态并发生模态转换。而悬链线式的布置形式使得流场沿立管结构展向的分布不是均匀的。立管空间形态受反向流作用，曲率和张力沿展向的改变使得水动力分布更为复杂。可以看到反向流作用下，悬链线立管沿展向的振动幅值要大于立管在正向流作用下的表现，尤其在高速来流的情况下表现得更加明显，这一现象在工程中应引起注意。

3.3 立管控制模态与空间形态分析

由于涡激振动现象主要出现在立管的悬垂段，因此本文只研究立管悬挂点到触地点之间的振动规律。通过统计VIV无因次振幅沿立管展向的空间分布，能够反映立管在海流作用下发生VIV的振型与控制模态。图10和图11给出了正向流和反向流时，不同潮流流速下立管CF方向无因次振幅A/D平均值沿立管展向的分布。

从图10和图11可以看出，柔性立管在CF方向VIV响应控制模态与潮流流速呈正相关。在正向潮流流速为0.2 m/s和0.4 m/s时，控制模态分别为1阶和3阶，在0.6 m/s，0.7 m/s、0.8 m/s流速下控制模态为4阶，在1.0 m/s和1.2 m/s时分别为5阶和6阶。另一方面，在反向来流时，0.2～1.0 m/s的控制模态与正向流保持一致，不同的是1.2 m/s时控制模态仍然为5阶。

图10 正向流时立管CF方向的无量纲位移均值随流速变化

这表明潮流流速的变化会引起柔性立管激发不同的控制模态，流速越大时，高阶模态的出现将会加速立管的疲劳损伤。此外，还可以明显看出，悬链线式柔性立管在CF方向具有非常明显的行波特性，即除了悬挂点和触底点外，柔性立管的中间段不存在恒为0的驻点。

通过对比图10和图11中柔性立管的振动幅值沿立管轴线的变化，可以发现在低流速情况下，柔性立管在整个轴线上具有相同的VIV响应幅值，在高流速情况下，柔性立管面对正向流和反向流的VIV响应则有明显的区别。正向流时柔性立管的VIV响应幅值在立管上部较大，沿着轴线方向逐渐降低，而在触地点附近又增加。可以看出结构响应的最大幅值点随着流速的增加而向张力较大的位置移动，这与VANDIVERJK[17]的大尺度试验观察到的现象是一致的。而反向流作用时立管在悬垂段中间位置的VIV响应最为明显，靠近两端则逐渐变弱。产生这种现象的原因与立管的空间形态有关，这主要是由于柔性立管的悬链线姿态受到改变所造成的。

由于柔性立管的柔性较大，抗弯刚度小的特性，整体姿态受潮流的影响较大。图12给出了潮流流速U为0.4 m/s、0.8 m/s和1.2 m/s时立管空间形态随潮流流向的变化。可以发现，立管受正向流作用时，立管能够较好保持悬链线姿态，而在反向流作用下，立管悬垂段曲率改变更为明显，因此中间部分受VIV响应影响较大。立管轴线上曲率分布出现两个极值点，分别在悬挂点和触地点附近，随着流速的增加而不断增大，在不同的流向下曲率幅值变化较为剧烈，这表明立管这两段部分为危险区域，在涡激振动影响和往复来流作用下将会加剧管线的疲劳破坏，在工程应用中应予以关注。

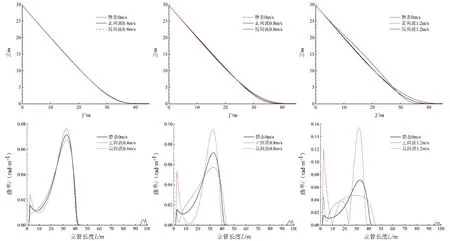
图12 立管整体姿态随流速和流向变化

4 结 论

本文研究了海洋潮流流速和流向的改变对非金属柔性立管的动力响应特性的影响。根据海上模型试验数据，采用水动力学软件OrcaFlex建立柔性立管悬链线模型，分析了立管张力、固有频率、VIV动力响应和控制模态等响应特性，研究结论如下。

（1）潮流流向对立管顶部张力和VIV响应特性影响很大。正向流时，流速越大，顶部张力越大，在0.7 m/s流速下立管动力响应最为显著，在低速和高速情况下响应振幅减小。而在反向流时，顶张力随着流速增大而减小，立管展向的VIV响应幅值与流速呈正相关，在1.2 m/s时达到最大值。

（2）潮流流速直接影响立管的运动特性。柔性立管控制模态与潮流流速的变化呈正相关，并呈明显的行波特性，其中高流速情况下，正向流比反向流更容易激发立管的高阶模态，这与立管的空间形态有较大影响。由立管VIV振幅沿展向分布可以看到，低流速时，柔性立管在悬垂段上具有相同的VIV响应幅值。高流速情况下，正向流作用时柔性立管的VIV响应幅值在立管上部较大，沿着轴线方向逐渐降低，而在触地点附近又增加。而反向流作用时在悬垂段中间部分VIV响应幅值最大。

（3）悬链线式柔性立管的空间形态受潮流流速和流向影响较为显著。悬挂点和触地点附近曲率出现极大值点，不同潮流流向下曲率幅值变化较为剧烈，可知在往复来流时两处易发生疲劳损伤，建议在布设管线时考虑当地潮流特征，以减小管线损坏风险。本文研究可为海洋柔性立管总体布置设计提供参考。