Observation and modelling of snow and sea ice mass balance and its sensitivity to atmospheric forcing during spring and summer 2007 in the Central Arctic

Bin CHENG, Timo VIHMA, Timo PALO, Marcel NICOLAUS, Sebastian GERLAND, Laura RONTU, Jari HAAPALA & Donald PEROVICH

1 Finnish Meteorological Institute, Helsinki Fi-00101, Finland;

2 University of Tartu, 50090 Tartu, Estonia;

3 Alfred Wegener Institute Helmholtz Centre for Polar and Marine Research, Bremerhaven, Germany;

4 Norwegian Polar Institute, Fram Centre, Tromsø, Norway;

5 Thayer School of Engineering Dartmouth College, Hanover, New Hampshire, USA

Abstract Snow depth and sea ice thickness were observed applying an ice mass balance buoy (IMB) in the drifting ice station Tara during the International Polar Year in 2007. Detailed in situ observations on meteorological variables and surface fluxes were taken during May to August. For this study, the operational analyses and short-term forecasts from two numerical weather prediction (NWP) models (ECMWF and HIRLAM) were extracted for the Tara drift trajectory. We compared the IMB,meteorological and surface flux observations against the NWP products, also applying a one-dimensional thermodynamic sea ice model (HIGHTSI) to calculate the snow and ice mass balance and its sensitivity to atmospheric forcing. The modelled snow depth time series, controlled by NWP-based precipitation, was in line with the observed one. HIGHTSI reproduced well the snowmelt onset, the progress of the melt, and the first date of snow-free conditions. HIGHTSI performed well also in the late August freezing season. Challenges remain to model the “false bottom” observed during the melting season. The evolution of the vertical temperature profiles in snow and ice was better simulated when the model was forced by in situ observations instead of NWP results. During the melting period, the nonlinear ice temperature profile was successfully modelled with both forcing options.During spring and the melting season, total sea ice mass balance was most sensitive to uncertainties in NWP results for the downward longwave radiation, followed by the downward shortwave radiation, air temperature, and wind speed.

Keywords Arctic, snow melt, sea ice mass balance, snow on sea ice, NWP models

1 Introduction

Arctic sea ice and its snow cover are sensitive components of the climate system. They act as strong reflectors of solar radiation and, for most of the year, as efficient insulators between the relatively warm ocean and the colder atmosphere. The marine Arctic climate system is rapidly changing (Döscher et al., 2014; Vihma et al., 2019; Meier et al., 2021) and, due to their smaller heat capacities compared to seawater, sea ice and particularly its snow pack are the most sensitive components of the system. The ice thickness,volume, and multiyear ice coverage have all reduced during the past six decades (Kwok, 2018). Melting of sea ice yields freshwater to the upper ocean during summer (Carmack et al., 2016; Perovich et al., 2021).

Snow affects the mass balance of sea ice via its insulating effect, which reduces ice growth in autumn,winter, and most of spring, and via its reflective effect,which protects sea ice from solar radiation in spring and summer. However, snow also contributes to sea ice growth via refreezing of slush generated by snowmelt (Nicolaus et al., 2003; Granskog et al., 2017; Provost et al., 2017;Webster et al., 2018) or flooding, the latter being less common in the Arctic. Spring snow cover has thinned in the Beaufort and Chukchi seas, and elsewhere in the western Arctic (Webster et al., 2014). The spring onset of snowmelt has become earlier (Markus et al., 2009), mostly controlled by downward longwave radiation (Maksimovich and Vihma,2012), and the increased snowmelt has resulted in earlier melt pond formation in summer, particularly north of 80°N(Rösel and Kaleschke, 2012).

Autonomous sea ice mass balance buoys (IMB),consisting of a thermistor string and acoustic sounders, have demonstrated a good applicability in observing long-term evolution of sea ice and snow thickness as well as the temperature profile from the ocean through the ice and snow to the atmosphere (Richter-Menge et al., 2006;Polashenski et al., 2011; Jackson et al., 2013; Lei et al.,2018). To understand the physical processes of snow and sea ice heat and mass balance, thermodynamic snow and sea ice models are often applied. Modelling of sea ice thermodynamics have been carried out for many years.Previous modelling studies have demonstrated the importance of accurate boundary conditions (Maykut and Untersteiner, 1971) and energy conservation (Bitz and Lipscomb, 1999), model vertical resolution in snow and ice(Cheng et al., 2008), the oceanic heat flux at the ice base(Polyakov et al., 2010), and snow-ice interactions (Cheng et al., 2013; Wang et al., 2015). However, for comparison between observations and model results, data on long-term evolution of snow and sea ice thickness and vertical temperature profiles are still a rarity, especially in the Central Arctic Ocean.

Thermodynamic sea ice models are commonly externally forced by

in situ

observations or numerical weather prediction (NWP) models.

In situ

forcing data have usually a small footprint and comparably high accuracy, and they are often used for model development and validation.However, for operational services, one has to rely on NWP results as forcing, although NWP models still have large uncertainties over sea ice. Due to sparsity of observations,even more uncertainty is related to the oceanic heat flux,which varies a lot in space and time (Krishfield and Perovich, 2005; Stanton et al. 2012). The difference between the oceanic heat flux and the conductive heat flux upwards through the sea ice controls the basal growth or melt rates (Makshtas, 1991). In the latter half of the melt season, when the ice layer is often close to isothermal, the ice bottom melt rate is controlled by the heat flux from ocean (Lei et al., 2014; Ackley et al., 2015; Leppäranta,2015).Information on sea ice and snow thickness in the Arctic Ocean is still sparse. To better understand the ongoing and future changes in the Arctic sea ice and snow and their interaction with the ocean and atmosphere,improvements are needed in observations, process understanding, models, and use of observations in models.In this study, we present IMB observations in undeformed sea ice at the drifting ice station Tara (Gascard et al., 2008)in the Central Arctic Ocean from May to November 2007.The temporal evolution of IMB data on snow depth, ice surface ablation, bottom freezing and melting, as well as snow and ice temperature profiles were analysed. A one-dimensional thermodynamic snow and sea ice model was applied to simulate the evolution of snow and ice temperature profiles and mass balance. The

in situ

meteorological observations and NWP model analyses and forecasts were used as external forcing. The observed and modelled snow and ice thickness and temperature profiles were compared.There have been several drifting-ice-station campaigns implemented in the Arctic in the past a few decades. Various in-situ observations have been carried out. Although Tara field observations are not new,

in situ

observations are always valuable for model validation and process studies,especially along the transpolar stream. Several previous studies have addressed the spatiotemporal variability of atmospheric and oceanic forcing on snow and sea ice mass balance through investigation of in-situ observations(Nicolaus et al., 2010; Haller et al., 2014; Haas et al., 2017).In this paper, we focus on modelling of spatiotemporal variations of snow and ice mass balance during the spring-summer season in the central Arctic, which has not received much attention so far. The period of Tara observations is particularly interesting, as it preceded the lowest September sea-ice concentration observed ever before (Zhang et al., 2008). Further, summer 2007 represented a transition from the earlier, multi-year sea-ice dominated Arctic to recent, more first-year sea-ice dominated Arctic (Tschudi et al., 2020).

In this study, we pay particular attention on IMB observations, modelling of snow and ice mass balance, as well as its sensitivity to uncertainties in the NWP-based atmospheric forcing during spring and the melting season.Through this comprehensive investigation, we expect to better understand the linkages between sea ice changes,model forcing, and model results. The objectives of the study are (1) to identify the requirements for better sea ice and snow measurements in the Arctic Ocean, (2) to find out the most critical atmospheric factors for sea ice mass balance in spring and summer, and (3) to evaluate the performance of existing modelling approaches and present perspectives for their improvement.

2 Data and method

2.1 Tara drifting ice station

The drifting ice station Tara (Figure 1) was a major component of the European Commission (EC) funded project DAMOCLES (Developing Arctic Modelling and Observing Capabilities for Long-Term Environmental Studies) (Gascard et al., 2008). The French schooner Tara was frozen into sea ice and drifted along the Transpolar Drift Stream across the Arctic Ocean. The Tara was moored in sea ice on 4 September 2006 north of Laptev Sea, and broke free on 21 January 2008 in Fram Strait. Most devices for sea ice and snow observations were deployed between 22 and 30 April 2007, and the observations continued towards the end of 2007 (Nicolaus et al., 2010).

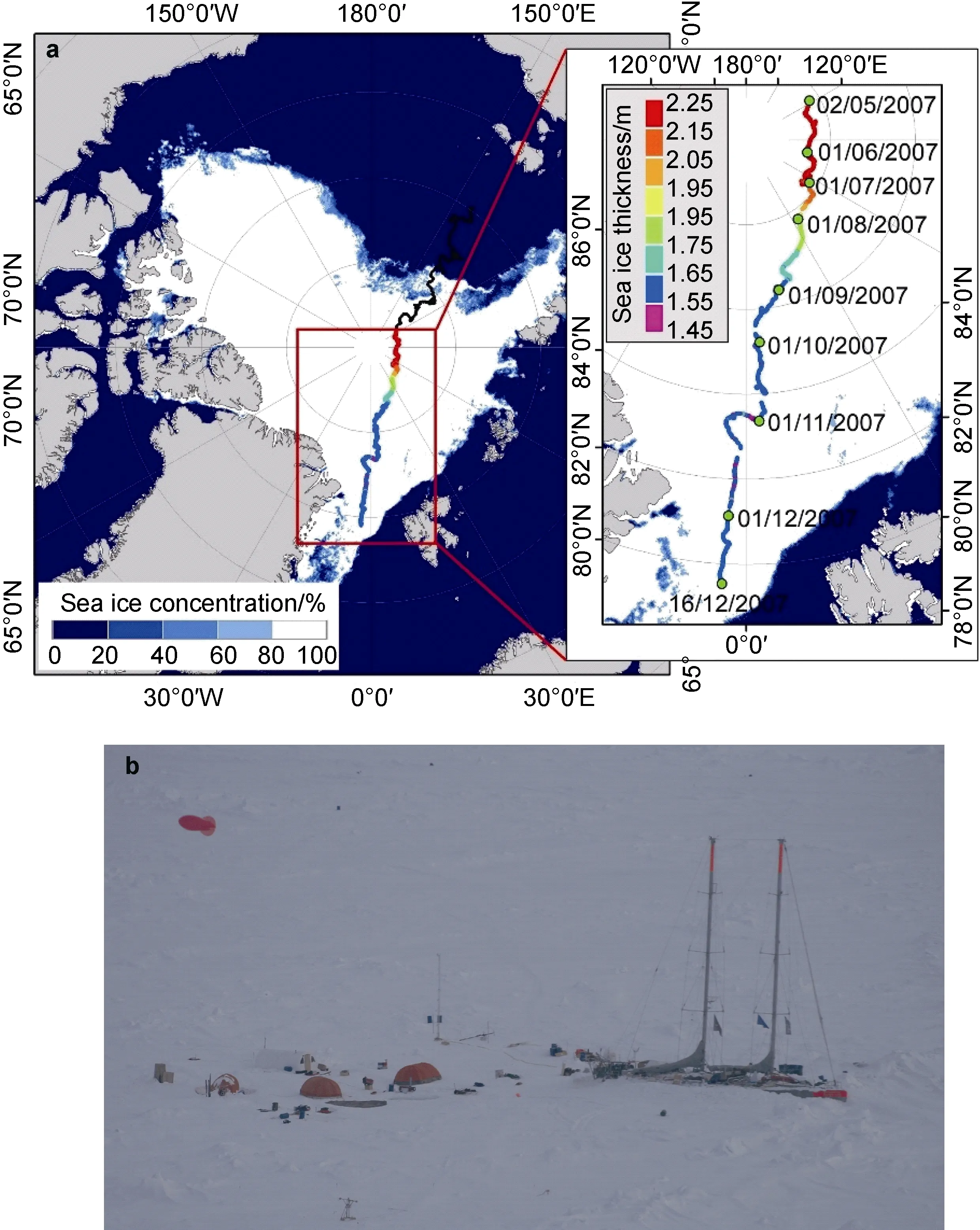
Figure 1 a, The drift trajectory of Tara between 5 September 2007 and 7 November 2007. The colored line zoomed on the right frame indicates the ice thickness measured by an ice mass balance buoy (IMB) deployed nearby Tara between 1 May and 16 December 2007. The background ice concentration represents the conditions on 16 September 2007. b, An aerial view of the Tara camp in late April 2007 (Photo by Tara field camp crew).

2.2 Weather data

Measurements of the meteorological conditions on the ice were performed between 1 May and 3 August 2007. The variables used in this study are wind speed (

V

) and air temperature (

T

) at 10 m height and air relative humidity(

Rh

) at 2 m height. These variables were recorded at 2-minute intervals and averaged to obtain hourly values.The downward (

Q

) and upward (

Q

) shortwave and the downward (

Q

) and upward (

Q

) longwave radiative fluxes were measured using a pair of Eppley PSP pyranometers and a pair of Eppley PIR pyrgeometers facing upward and downward, respectively. The radiation measurements were made at 1-minute intervals and averaged to obtain hourly values. The surface albedo (

α

) was derived from

Q

and

Q

.Hourly means of both meteorological parameters (

V

,

T

,

Rh

)and radiative fluxes (

Q

,

Q

), and

α

were applied as external forcing for the ice model.

2.3 Ice mass balance

An ice-mass-balance buoy (number 2007C) produced jointly by MetOcean (http://www.metocean.com/) and the US Army Cold Regions Research and Engineering Laboratory (CRREL) was deployed on 23 April 2007(Nicolaus et al., 2010). Acoustic sounders were mounted looking downward above the snow surface and looking upward below the ice bottom. The surface and bottom positions were measured, and the snow depth and ice thickness were derived. A 5-m-long thermistor string was applied to measure the vertical temperature profile from near-surface air through snow and ice to the ocean. The vertical sensor interval was 10 cm. Both acoustic and temperature measurements were made every 2 h. At the time of the IMB deployment, there were six thermistor- sensors located above the snow surface. Reliable measurements of snow depth, ice thickness and the temperature profile lasted from 2 May to 20 November 2007 (Figure 2).

In early May, snow pack around Tara was thin (5-10 cm) compared with a 20 cm snow depth observed during the same period at the North Pole (Gerland and Hass, 2011).At the IMB site, snow depth increased from the initial 5 cm up to 12 cm by 10 June before the snowmelt started. The snow melted completely by 22 June and started to accumulate again on 14 August. By the end of August, the snow had accumulated to 22 cm. The snow depth was also measured at a snow stake by visual readings some 250 m away from the IMB site, and the results showed very similar temporal evolution compared with the IMB measurements (Nicolaus et al., 2010). From 1 September to 20 November, the IMB sounder revealed several episodes of snow depth increase on a short time scale of 1-2 d. These events were most probably associated with snowfall. The snow depth increased from 22 cm by the end of August up to 48 cm on 19 October. Between 19 and 21 October, the sounder recorded a sudden drop of snow depth by 15 cm,followed by an immediate 10 cm increase and a further increase up to 55 cm on 27 October. The thermistor string data showed a sharp gradient at the same layers indicating that the uppermost sensors were indeed in the snowpack.The oscillation of snow depth around 20 October most probably resulted from a combination of snowfall and snowdrift.

The ice thickness was 214 cm on 1 May and increased to 225 cm due to basal growth until 22 June. From 22 June to 14 August, the ice surface melt was 53 cm but the basal growth was 6 cm. The basal melt was recorded after ice surface melt stopped and snow started to accumulate on 14 August. The basal melt was 20 cm from 14 August until 20 November. The latest recorded ice thickness was 160 cm.The evolution of snow and ice thickness revealed by temperature profile measurements (Figure 2a) was consistent with that based on the acoustic sensors(Figure 2b).

Figure 2 a, The IMB temperature profiles measured on 2 May,10 August and 20 November 2007. The circles represent the data from the locations of the temperature sensors. The upper blue dashed line marks the initial ice surface when the IMB was deployed. The lower blue line is the ice surface on 10 August deteced by sounders. The green circles indicate sensors located in the air. Negative value was defined below initial ice surface. b,The temperature and thickness of snow and ice measured by IMB during the period from 1 May to 20 November, 2007. In the vertical axis, zero refers to the initial air-snow interface. The black lines are the acoustic sounder observed surface/bottom 5-day moving average evolution.

2.4 Products of NWP models

The operational analyses and short-term forecasts of the European Centre for Medium-Range Weather Forecasts(ECMWF) and the HIgh Resolution Limited Area Model(HIRLAM, Undén et al., 2002) were available for this study.The ECMWF operational analyses were available with 6 h intervals. However, as there are no operational analyses on radiative fluxes and precipitation, the downward components of the solar shortwave and thermal longwave radiation were based on the ECMWF 12-h accumulated operational forecasts (00 and 12 UTC + 12 h), and the precipitation on 24-h accumulated forecasts (00 UTC +24 h). The lateral model spatial resolution was 0.225°. The 10-m

V

, 2-m

T

, and

Rh

, the cloudiness (

CN

), snow precipitation

(PrecS),

Q

and

Q

were the variables applied as forcing for HIGHTSI.

The HIRLAM (version 7.4) experiments were made over an Arctic domain (4E-140E, 85N-89N) (Figure 1b)with a horizontal resolution of 15 km and 60 vertical levels.As a limited area model, the lateral boundary conditions of HIRLAM were taken from ECMWF analyses and forecasts.The output variables were the same as for the ECWMF.

All NWP data were linearly interpolated to 1 h time intervals. The ECMWF results were bilinearly interpolated to a higher spatial resolution (0.1125°). Values from the nearest point of the (interpolated) grid along the Tara trajectory were used.

2.5 HIGHTSI model and configurations for this study

HIGHTSI is a one-dimensional thermodynamic snow/ice model targeted to solve temperature and mass balance(Launiainen and Cheng, 1998). HIGHTSI solves the snow/ice surface heat budget, the solar radiation penetrating the snow and ice, the heat conduction in the snow and ice,and the ice bottom heat and mass balance. The turbulent surface fluxes are parametrized considering the thermal stratification. The penetration of solar radiation into snow and ice depends on the cloud cover, surface albedo, snow structure and density, and colour of the sea ice, making the extinction coefficient a time dependent parameter with a large range of variability (Table 1). This allows quantitative calculation of sub-surface melting (Cheng et al., 2003,2006). Short- and long-wave radiative fluxes can be either parametrized or prescribed based on

in situ

observations or NWP model results. The heat flux and mass balance as well as snow/ice phase transformation are calculated at the interfaces of air/snow, air/ice, snow/ice, and ice/ocean(Cheng et al., 2008).The essential forcing parameters for HIGHTSI are

V

,

T

,

Rh

,

Q

,

Q

as well as snow precipitation (

PrecS

). The model experiment defined as the reference control run was based on forcing by

in situ

observations and covered the period from 1 May to 3 August. During the Tara expedition,unfortunately

PrecS

measurements were not made. We therefore applied ECMWF snow precipitation. A snow density of 320 kg·mwas used to convert the snow water equivalent to snow depth (Huwald et al., 2005).At the sea ice bottom, the oceanic heat flux (

F

) varies in time and space. The variations are related to the seasonal evolution of upper-ocean temperature (Lei et al., 2014) and the solar heating of the ocean due to regional appearance of open leads and changes in ice concentration in summer(Perovich, 2011). Lacking direct

F

measurements, we estimated it based on the IMB measurements of ice thickness and in-ice temperature (Lei et al., 2010). At the ice bottom, the difference between the conductive heat flux

k

/(∂

T

/∂z) and

F

determines the ice growth rate

ρ

L

(d

h

/d

t

), where ∂

T

/∂z represents the vertical gradient of in-ice temperature

T

near the ice bottom,

L

is the latent heat of fusion of sea ice,

h

is ice thickness, and

z

and

t

are the depth and time, respectively. The bottom ice growth of 10 cm from early May until onset of surface ice melting on 21 June represents an average ice growth rate of 1.9 mm·d.The conductive heat flux near the ice bottom was calculated using the thermistor string data. The heat conductivity of sea ice was calculated based on Pringle et al. (2007), using average sea ice temperature and mean sea ice salinity of 4 ppt (Nicolaus et al., 2010). As the latent heat of fusion of sea ice is 333.4 kJ·kg, to generate 10 cm ice growth over 52 d, the average oceanic heat flux should have been about 1 W·m.During the study period the ice floe of the Tara camp was relative stable, and no large areas of open water were detected near the IMB in May and June. Melt ponds were detected in the vicinity of Tara but only for a relatively short time period in the second half of July (Sankelo et al., 2010).During the melt season,

F

was likely to increase due to solar heating. We assumed

F

= 1 W·mfor the freezing period (1-22 June) and

F

= 2 W·mfor the rest of the modelling period. The initial snow and ice temperature profiles were defined according to the IMB measurements.The model parameters are summarized in Table 1. We applied the observed surface albedo in all model experiments to reduce the uncertainties of shortwave radiative flux. The model had 20 layers in sea ice and 10 layers in snow. The time step was 1 h.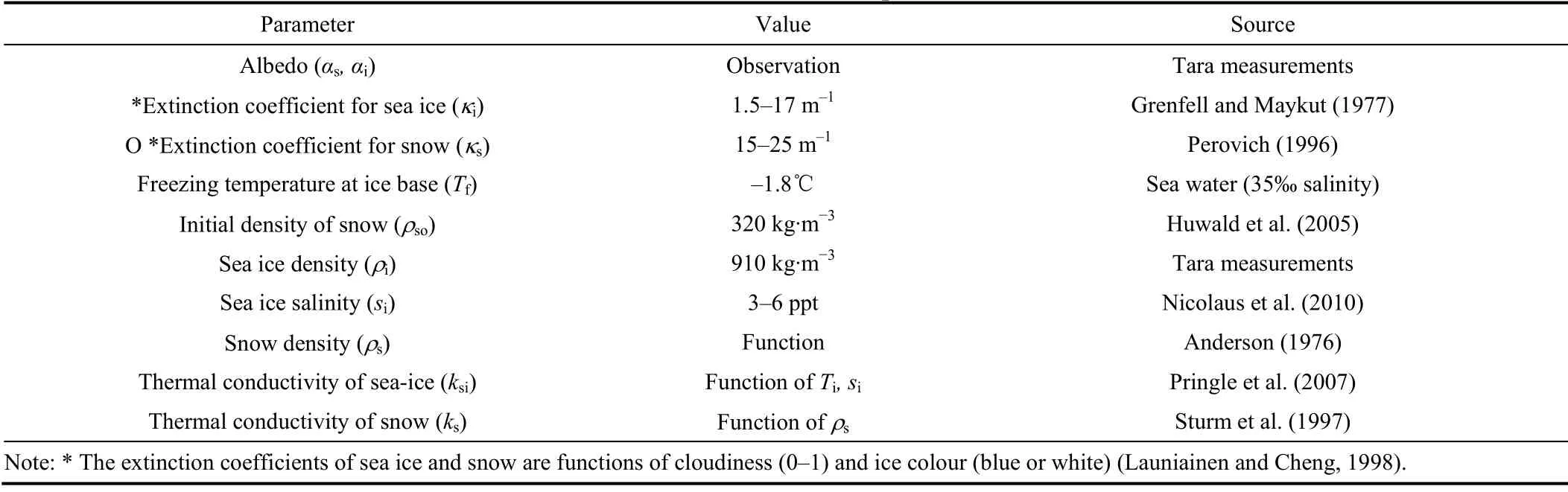

Table 1 HIGHTSI model parameters

2.6 HIGHTSI model experiments

Several model experiments were made. The reference run(REF) was used to assess the performance of the HIGHTSI model, with minimal impact from uncertainties in the atmospheric forcing. Hence, HIGHTSI was forced by the Tara

in situ

observations, except that precipitation was based on the ECMWF 24-h accumulated forecasts. The differences between the Tara observations and NWP model results originated from various factors, such as inaccuracies in the NWP model initialization, the resolved dynamics of weather systems, and the parameterization of sub grid-scale processes. To investigate the sensitivity of snow and sea ice mass balance to the inaccuracy of atmospheric forcing, we carried out HIGHTSI sensitivity experiments. Those experiments, entitled as EC and HIR, were forced by the analyses and short-term forecasts of the ECMWF and HIRLAM models, respectively.Comparing the results of REF, EC and HIR yield information on the impact of the uncertainty of the modelled atmospheric forcing on snow and ice mass balance. In addition, we carried out the following sensitivity experiments

V

-EC,

T

-EC,

Q

-EC,

Q

-EC,

V

-HIR,

T

-HIR,

Q

-HIR, and

Q

-HIR, where

V

refers to wind speed,

T

to air temperature,

Q

to downward shortwave radiation, and

Q

to downward longwave radiation. In these experiments,the selected atmospheric forcing variable was based on the ECMWF or HIRLAM model output, but the other atmospheric forcing variable were based on the Tara observations. Hence, these experiments yielded information on the impact of the uncertainty of individual atmospheric forcing variables, allowing identification of the forcing variables associated with most critical uncertainties from the point of view of snow and ice mass balance. Finally, we wanted to understand how representative the Tara observations were for snow and ice conditions along the Transpolar Drift Stream. Hence, we made a sensitivity experiment EC-100 that was otherwise identical to EC, but the ECMWF model output was taken from a trajectory parallel to that of Tara but located 100 km northwest of it.To access solely the impact of weather forcing, we assumed the same initial conditions of snow depth, ice thicknesses and temperature profile as applied in the EC experiment.

3 Results

3.1 Assessment of NWP results

The reliability of modelling results largely depends on the quality of forcing data. We applied a double linear interpolation procedure to calculate the ECMWF and HIRLAM output variables along the Tara drift trajectory using the nearest grid-point values picked from the models(best match to the Tara location from NWP model grids).Figure 3 shows the time series of Tara observed and NWP modelled weather parameters along Tara track. Figure 4 shows the probability density function (PDF) of Tara observed and NWP modelled meteorological parameters.Table 2 gives statistical analyses of the NWP results.

The modelled wind speed, in general, well reproduces the temporal variation of observations (Figure 3a). However,both NWP models tended to overestimate low wind speeds and underestimate high wind speeds. For example, in the case of observed wind speeds less than 2 m·s, the NWP modelled wind speeds were, on average, 1.7 m·s(ECMWF) and 1.8 m·s(HIRLAM) too high, whereas for observed wind speeds higher than 8 m·s, the NWP wind speeds were, on the average, 1 m·s(ECMWF) and 3 m·s(HIRLAM) too low. The ECMWF average wind speed(4.6 m·s) was slightly higher than that of HIRLAM(4.1 m·s) and had a better correlation with observations(Table 2).

The temporal variability of modelled and observed air temperature agreed to each other (Figure 3b). However, the NWP models overestimated the lowest air temperatures.The ECMWF and HIRLAM produced the same average air temperature. Both ECMWF and HIRLAM air temperature showed a positive bias (1.7℃ ) compared with the observations. During the melting season, however, the agreement was better. The ECMWF relative humidity agreed better with Tara observations than that of HIRLAM.Before the start of the melting season, the average HIRLAM relative humidity was 12% larger than the ECMWF result. During the melting season, the modelled mean values of relative humidity were 97% for ECMWF and 96% for HLRLAM that were closed to each other and to observations (94%). However, on a few occasions the measurements suggested large temporal variations of relative humidity, while the modelled values remained stable (Figure 3c). The radiative fluxes, in particular their temporal variability differed for observations and NWP products (Figures 3d, 3e).

The modal of wind speed was 4 m·samong

in situ

observation and results of NWP models (Figure 4a). The main modal of air temperature was 0℃ because half of the data period was in summer. The observed and modelled

T

distributions agreed well in the range from -5℃ to +2℃(Figure 4b). NWP models yielded moister air compared with observaitons (Figure 4c). The ECMWF relative humidity agreed better with Tara observations than that of HIRLAM (Table 2). The observed, ECMWF-based, and HIRLAM-based distributions of

Q

and

Q

differed from each other (Figures 3d, 3e; Figures 4d, 4e). This was mostly due to differences in clouds. The uncertainties in the treatment of the variable cloud properties by the NWP models are often the main source of the differences between modelled and observed radiation fluxes (Schreier et al.,2013). Unfortunately, we do not have reliable cloud observations to make a more extensive assessment. Overall,the absolute difference between ECMWF and observed

Q

(45 W·m) was larger than that between HIRLAM and observations (20 W·m). The biases were -45 W·mand-20 W·mrespectively, i.e., the modelled

Q

were underestimated. For smaller

Q

(＜ 250 W·m), the distributions of observations and NWP results agreed reasonably well. However, the HIRLAM model overestimated the large values (Figure 3e, Figure 4e). The correlation between the observed and modelled

Q

was larger than that of the

Q

(Table 2).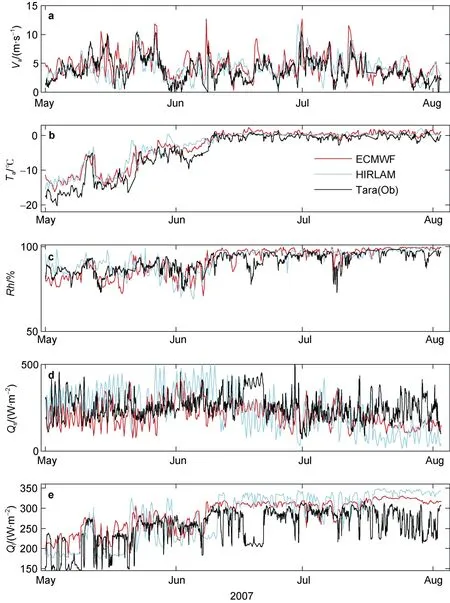

Figure 3 Time series of ECWMF (red line) and HIRLAM (cyan line) modelled and in situ observed (grey) variables of wind speed (Va, a),air temperature (Ta, b), relative humidity (Rh, c), downward shortwave radiative flux (Qs, d), and downward longwave radiative flux (Ql, e).

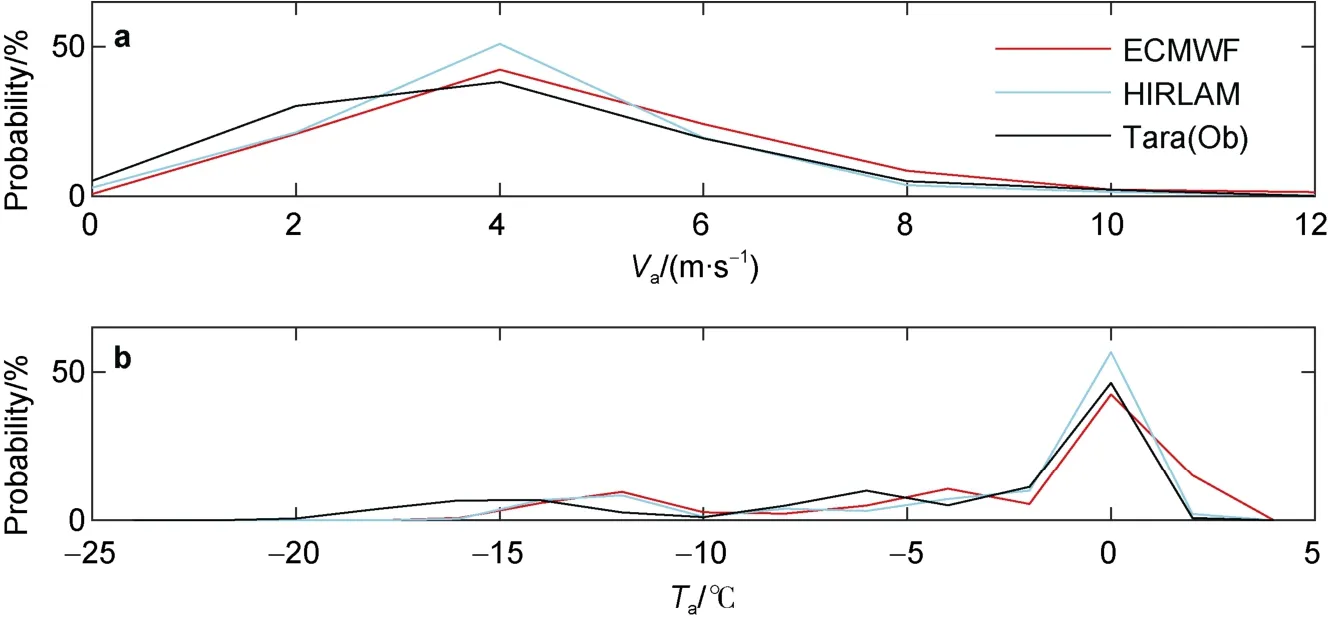
Figure 4 Probability density function (PDF) of Tara observed (red) and NWP modeled (ECWMF, green; HIRLAM, blue), Va, Ta and Rh sorted into 2 m·s-1, 2℃ and 2% bins, as well asQs and Ql sorted into 50 and 25 W·m-2 bins, respectively. The data include 2255 samples totally.

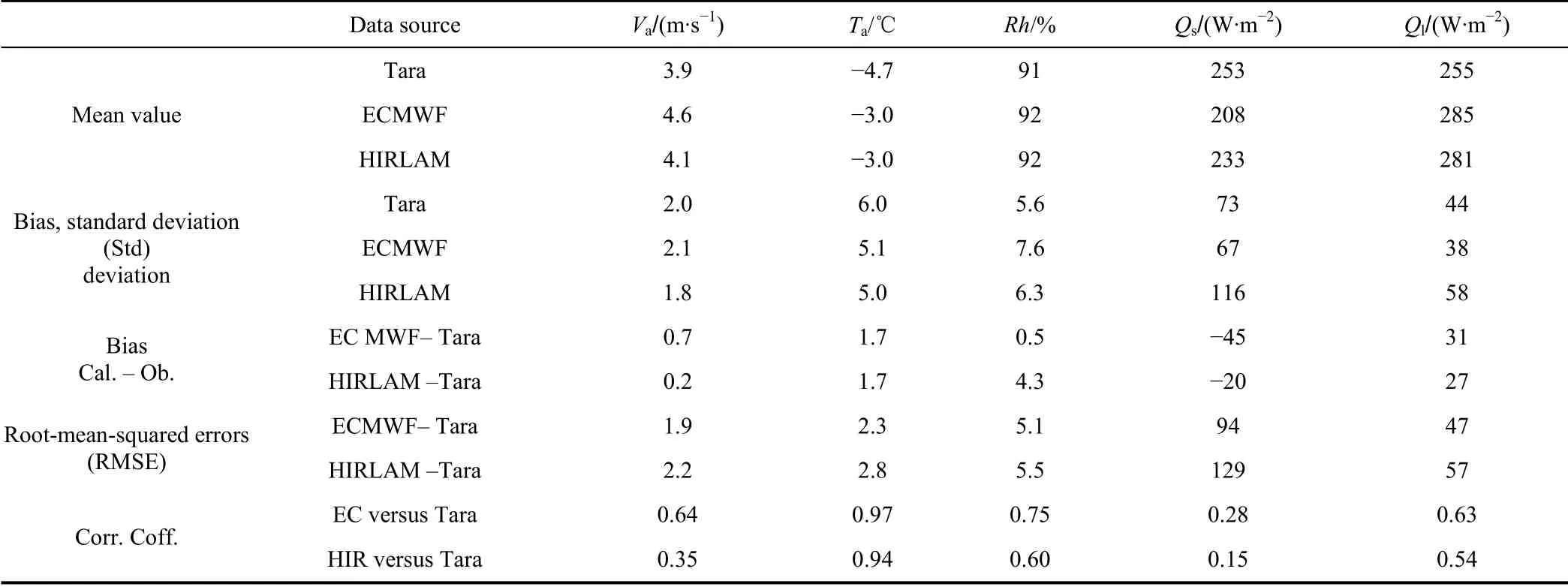
Table 3 Statistics of meteorological variables based on Tara observations as well as the operational analyses and short-term forecasts of the ECMWF (EC) and HIRLAM (HIR) from 1 May to 3 August 2007

3.2 Reference run

The modelled ice and snow evolutions were compared with the IMB measurements (Figure 5). From 1 May until 11 June, the accumulated snow precipitation in water equivalent was 16.6 mm based on the ECMWF model. This resulted in 5.2 cm snow depth increase, which was an underestimate by 1.8 cm compared with the IMB data. The timing of the modelled snowmelt onset was 10 June versus the observed onset on 7 June. The modelled and observed snowmelt rates and the snow-free dates were 10 mm·dand 9 mm·d, and 22 and 21 June, respectively. The modelled timing of ice melt onset agreed with observations partly due to the good simulation of snowmelt onset. During the simulation period, the IMB measured 0.4 m surface ice melt compared to the model result of 0.34 m. The errors of modelled surface heat fluxes contributed to the difference(Section 3.4).

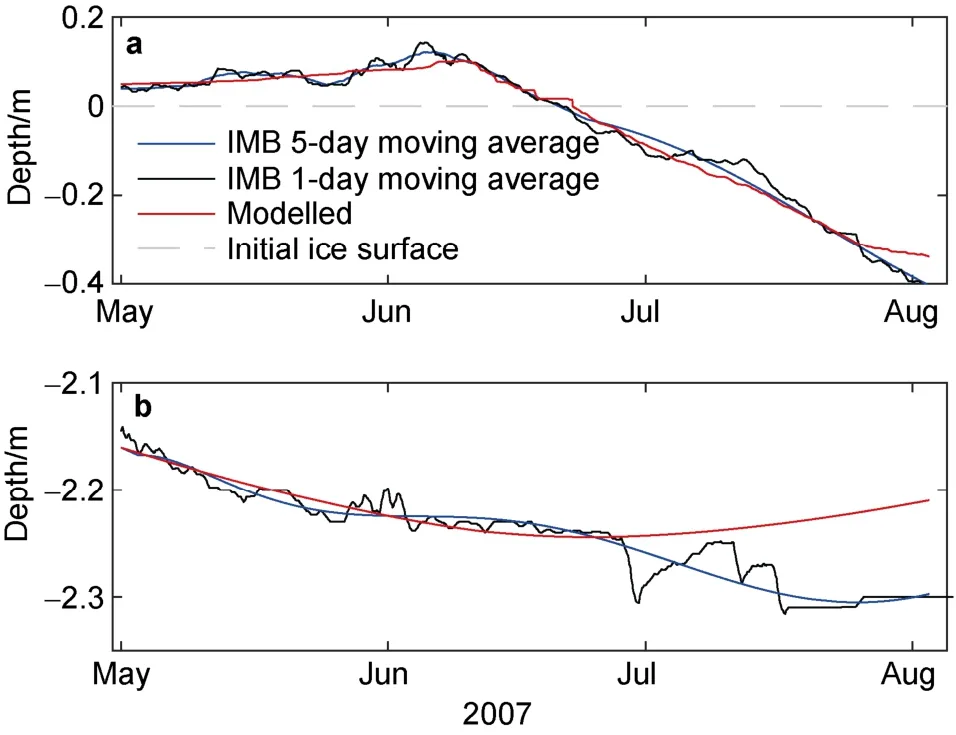
Figure 5 IMB observed and HIGHTSI modelled (reference run)time series of surface evolution (a) and bottom evolution (b). The blue and black lines are IMB 5-day and 1-day moving average results. The ice growth in late June is due to a false bottom formation.

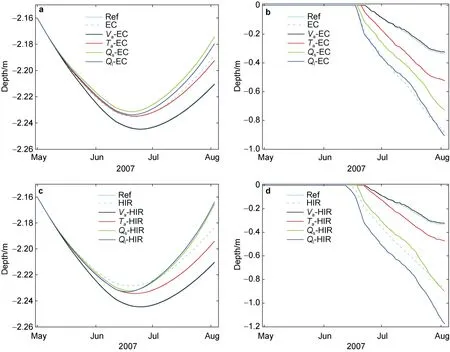
Figure 6 Results of model sensitivity experiments for mass balance at the ice bottom (a, c) and ice surface (b, d), for the experiments with forcing from the ECMWF (a, b) and HIRLAM (c, d) models. The line types represent the various sensitivity experiment. “Ref” marks the reference run. EC and HIR are model runs using entire ECMWF or HIRLAM results as forcing.

The modelled ice bottom evolution was in good agreement with IMB measurements until the end of the snow-covered period. The model run yielded 7.1 cm bottom freezing until 14 June followed by 6.5 cm melting by the end of the simulation. The modelled ice thickness agreed well with the IMB measurement until mid-June before the bottom melt was simulated. The IMB, however, revealed a further bottom freezing up to 8 cm until late July (5-day running mean). This freezing up at bottom during the melting season is likely a process called false bottom formation (Notz et al., 2003; Perovich et al., 2003). A “false bottom” is a thin layer of ice which forms in summer underneath the ice floe by meltwater that lies between the salty water and the sea ice. The source of meltwater and rate of its appearance are critical to determine the ice growth in summer. False bottoms may contribute to basal ice growth during the spring-summer period (Perovich et al., 2018).The surface ice melt onsite started on 19 June, which should have reduced ice surface albedo and increased solar radiation absorbed by sea ice and probably also the ocean below, enhancing bottom melting. The model experiment indeed suggested bottom melting after 19 June. During the melting season, the oceanic heat flux likely increases(Perovich and Elder, 2002) and would result in further melting at the ice bottom.

3.3 Sensitivity studies

The mean differences between ECMWF calculated and Tara observed

V

and

T

are 1.4 m·s, 1.8℃, and 1.7 m·s, 1.9℃ for HIRLAM. The mean values of

Q

and

Q

are 74 W·m,36 W·mfor ECMWF and 108 W·m, 47 W·mfor HIRLAM.The ice bottom mass balance and ice surface melt showed similar characteristics with respect to the sensitivities of both ECMWF and HIRLAM forcing data.The uncertainty of wind speed (

V

-EC,

V

-HIR) has no major impact on bottom ice mass balance and surface melting. Wind speed mainly affects the turbulent fluxes of sensible and latent heat but during spring and summer both fluxes were very small compared with

Q

and

Q

, resulting in a very small sensitivity to the wind speed. The uncertainty of air temperature (

T

-EC and

T

-HIR) affects ice mass balance both at the bottom and surface. The ice thickness varied by some 3 cm at the ice bottom in response to both ECMWF and HIRLAM

T

uncertainties. At surface,the uncertainty of

T

resulted in 19 cm increased melting for

T

-EC and 14 cm more melting for

T

-HIR. At the ice bottom, the sensitivities of ice mass balance to the

Q

(

Q

-EC,

Q

-HIR) and

Q

(

Q

-EC,

Q

-HIR) radiative forcing were close to each other for both ECMWF and HIRLAM.The effect was stronger than that of

T

. At the surface,however, the sensitivity of ice melting in response to the change of

Q

and

Q

differs from each other, respectively.The inaccuracy in the longwave radiative flux affects the most surface melting. The uncertainty of

Q

generated an increase in surface melting by 0.57 m for ECMWF and 0.84 m for HIRLAM, respectively. The corresponding values are 0.39 m and 0.57 m for

Q

.

3.4 Comparison of the freezing and melting periods

To better understand the model results, we divided the study period into two phases, the freezing period from 1 May to 9 June and the melting period from 10 June to 2 August. We present results that were derived from control reference run(Ref) as well as model experiments using solely EC and HIR output as external forcing. The observed and NWP-based forcing of

T

,

Q

and

Q

, as well as the modelled surface heat fluxes for both periods are presented in Table 4.During the freezing period, the net shortwave radiative flux affecting the surface heat balance (

Q

, not including the fraction penetrating below the model surface layer) did not vary much between the model experiments, whereas the net longwave radiative fluxes (

Q

) were different due to different

Q

(c.f. Table 4). The surface turbulent fluxes were small. Among the three experiments, differences mostly occurred between Ref and EC. The net radiative and turbulent heat flux acting at the surface (

Q

+Q

+Q

+Q

)was -32 W·m, -14 W·mand -23 W·mfor Ref, EC and HIR, respectively representing a heat loss. The surface conductive heat flux (

F

) was upward. The net surface heat flux

Q

: (

Q

+Q

+Q

+Q

+F

) was -0.8 W·m,12 W·mand 16 W·min Ref, EC, and HIR, respectively,i.e., the snow surface layer gained heat in EC and HIR, but not in Ref. There was no modelled surface melting in any of the experiments during the freezing period. Accordingly, the ice mass balance was dominated by the bottom heat budget,which generated freezing.

Table 4 Mean values of the forcing variables for HIGHTSI: air temperature (Ta) and downward radiative fluxes (Qsd, Qld), as well as the HIGHTSI model results for the surface fluxes, during the freezing and melting periods in Ref, EC, and HIR

During the melting period, the shortwave radiative flux dominated the surface net heat flux. The total radiative and turbulent heat flux at the surface (

Q

+Q

+Q

+Q

) was 12 W·m, 49 W·mand 50 W·mfor Ref, EC, and HIR,respectively, representing heat gain.

Q

was 22 W·m,43 W·mand 42 W·min Ref, EC, and HIR, respectively,demonstrating that in REF the conductive heat flux contributed to the heat gain at the surface, but not in EC and HIR. The larger surface heat gain in EC and HIR caused more surface melting than in Ref. The lower air temperature in Ref (-0.4℃ versus 0.6℃ for EC and 0.4℃ for HIR) and a smaller downward longwave radiative flux resulted in less surface melting.

The observed and modelled average temperature profiles for the freezing and melting periods are shown in Figure 7. During the freezing phase, the observed and modelled ice temperature profiles were quasi-linear and close to each other, indicating an upward heat conduction. During the melting season, the ice temperature profiles became nonlinear with the lowest ice temperature at a depth of about 0.6 m. This was modelled reasonably well in all experiments.The nonlinearity of the temperature profile was dominated by the variation of temperature and the salinity-dependent thermal conductivity of sea ice. Once melting occurred, the temperature profile became isothermal. The error analyses are presented in Table 5. During the freezing period, the vertical temperature distribution of Ref was more accurate than those of EC and HIR. The RMSE and biases were reduced during the melting period.

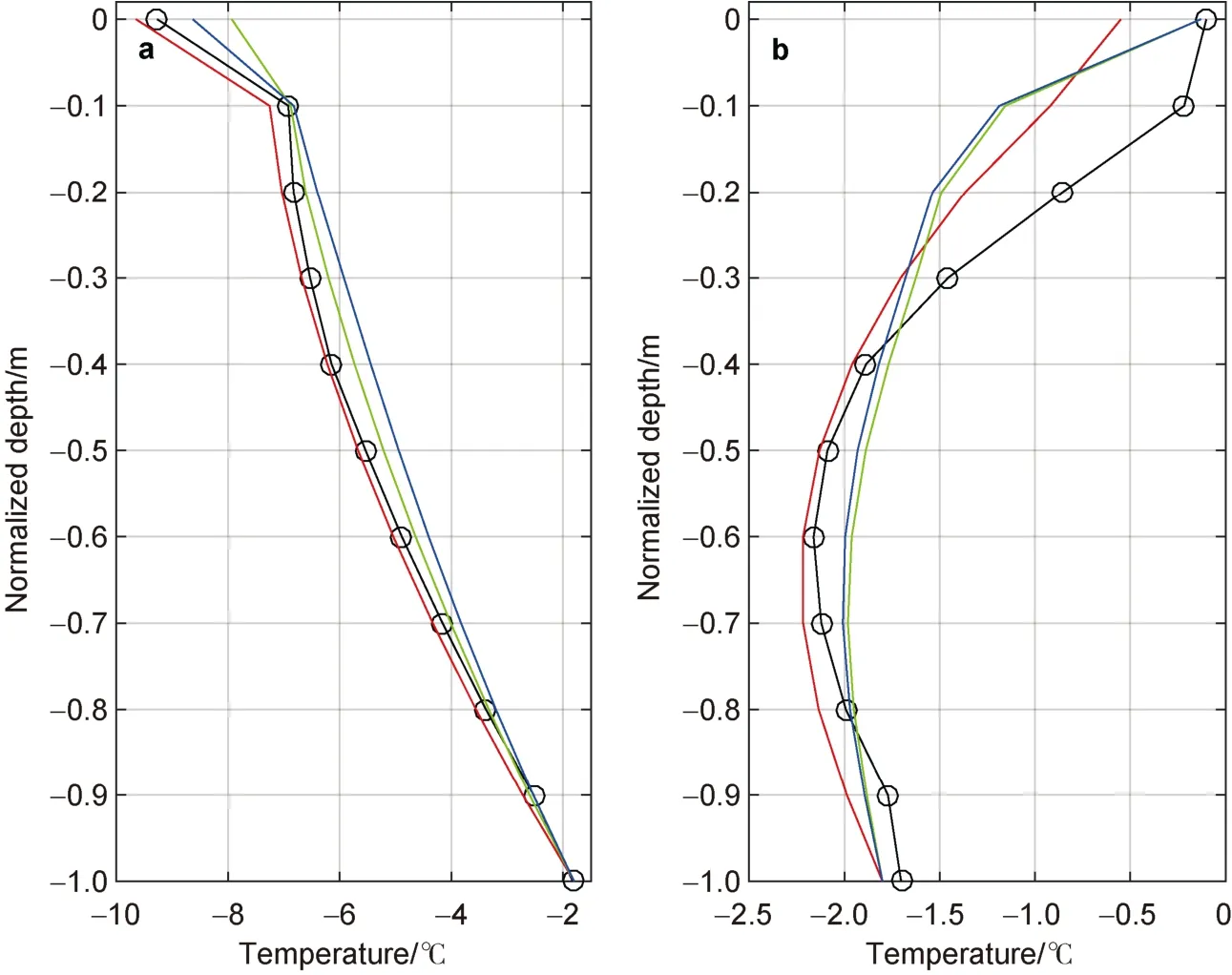
Figure 7 The modelled and observed mean vertical temperature profiles for the freezing period (a) and the melting period (b). The lines connected by black circles mark the IMB observations, and the model results are shown in red (Ref), blue (EC) and green (HIR) lines.

Table 5 The RMSE, Std, and correlation coefficient (R) between calculated and observed average vertical temperature profile of ice cover for the freezing and melting periods

3.5 Spatial variations of the ice mass balance

At a given time, the model represented conditions at a localized point, but the spatial variations of snow depth and ice thickness are complex. A full assessment of the spatial heterogeneity cannot be made without considering the dynamics and thermodynamics of the atmosphere, snow,sea ice and the ocean. However, simple model experiments can reveal the impact of weather forcing on spatial variation of snow and ice mass balance on a selected scale. Focusing on a scale of 100 km across the Transpolar Drift Stream, we compared the results of experiments EC and EC-100 (see Section 2.6). The modeled snow depth and ice thickness along the two trajectories showed highly correlated temporal evolution and, by the end of the study period, the results of these two experiments only showed a difference of 3 cm for the snow depth and 2 cm for the ice thickness.Hence, compared to spatial differences in weather forcing on a 100 km scale, the initial snow and ice conditions were more critical for spatial heterogeneity in snow and ice mass balance.

4 Discussions and conclusions

Snow and sea ice mass balance at the drifting ice station Tara in the Arctic Ocean in 2007 was investigated. We applied

in situ

meteorological and surface flux observations,IMB data, snow and ice model (HIGHTSI), as well as operational analyses and short-term forecasts from two NWP models. Along the Tara drift trajectory, the mean snow depth was 7 cm before the snow melt onset. The maximum ice thickness was 2.25 m in late June. A total of 53 cm ice surface melt was observed suggesting an average surface melting rate of about 1 cm·dduring the melting season. The latest recorded ice thickness was 1.6 m in the Greenland Sea.In early July, acoustic sounders detected a “false bottom”.The occurrence of a false bottom has been found in the Arctic Ocean prior to (e.g., Untersteiner and Badgley, 1958;Notz et al., 2003) and after (e.g., Wang et al., 2020; Lei et al.,2021) the Tara expedition. This phenomenon can occur not only in the central Arctic but also in the coastal landfast ice zone (Wang et al., 2013, 2020). The Tara

in situ

observation indicated that it was likely a short-lived process since this part of ice formation was quite fragile and potentially subject to a dynamic breakoff from the main ice column (Wang et al.,2020). The false bottom can be seen quite clearly from high resolution ice temperature regimes measured by the thermistor string-based ice mass balance buoy (Lei et al.,2021).

The HIGHTSI run, applying Tara observations as forcing, yielded onset of snow melt, onset of surface ice melt, and ice bottom growth that were in close agreement with the IMB measurements. During freezing conditions,the IMB ice thickness and ice temperature gradients suggested a small average oceanic heat flux of 1 W·mat the ice bottom. The oceanic heat flux is critical for ice bottom mass balance. During surface melt, the ice layer is close to isothermal, and the conductive heat flux close to zero. Hence, the oceanic heat flux alone controls the basal melt. After the end of the surface melt season, the basal melt results from the difference between the conductive heat flux and oceanic heat flux. Along the Tara trajectory,surface melting dominated sea ice mass balance during the melting period partly because during the Tara drift period the spring was particularly warm and the surface melting season was long (Vihma et al., 2008). The short-term impact of oceanic heat flux during the simulation period was limited. Accurate information on surface heat fluxes was critical for successful modelling of ice surface melting.Challenges remain in simulation of the “false bottom”observed during the melting season. Even if a model can simulate the ice formation, the ablation of “false bottom”might not be purely a thermodynamic process. Also, a dynamic break off may occur (Wang et al., 2020). There is need for more quantitative observational data on this process before it can be implemented in models.

The modelled evolution of snow depth, controlled by ECWMF-based snow precipitation, was in line with observations. Modelling of snow accumulation relies on the accuracy of precipitation, but

in situ

precipitation observations are seldom available from the Arctic Ocean.Because of a very limited amount of people in the Tara expedition after April, no continuous precipitation and snow drift observations were made. Although the reference run showed a good snow depth evolution, we still cannot conclude the quality of modelled snow accumulation, since it largely depends on the quality of precipitation data. Even in the case of precipitation measurements available, the locally measured snow depth may still be 2-3 times larger than the snow depth derived from precipitation measurements (as in the Surface Heat Budget of the Arctic Ocean (SHEBA) campaign; Huwald et al., 2005). In this study, HIGHTSI well reproduced the snow melt onset and the melting rate, but with errors on snow accumulation. The inaccuracy of NWP-based snowfall and the lack of snow dynamics in HIGHTSI

contributed to the differences. An advanced snow model (e.g., Liston et al., 2020; Wever et al.,2020) would be useful to better understand the role of snow dynamics on snow accumulation.The snow melt onset, the mean vertical temperature profile in snow and ice and ice bottom freezing were successfully modelled applying NWP results as forcing.Despite this, during the freezing period, the evolution of the snow and ice temperature profile was better represented in the model experiment using

in situ

forcing data than in the experiments using NWP results as forcing. During the melting period, the nonlinear profile of ice temperature was modelled well. The RMSE and STD between modelled and observed mean temperature profile were smaller using

in situ

forcing data than in the experiments using NWP results as forcing, but the differences were rather small. Hence, our results suggest that, from the point of view of the mean temperature profile, the ECMWF and HIRLAM products were reasonable to be used as forcing.

From the point of view of snow and sea ice thermodynamics, the main uncertainty of NWP model results lies in the radiative fluxes, which depend on cloud conditions, such as cloud liquid water and ice contents as well as cloud coverage and height. In particular, the NWP-based longwave radiative flux showed large differences from Tara observations. The accuracy of air temperature is also important for the ice mass at the ice surface and at the ice bottom. The surface melting was most sensitive to the longwave radiative flux followed by the shortwave radiative flux and the air temperature. During the Tara drift in spring and summer, the order of importance of NWP variables from the point of view of sensitivity of sea ice mass balance is as follows: the downward longwave radiative flux, downward shortwave radiative flux, air temperature and wind speed. The sensitivity was higher during summer than spring.

The errors in the modelled snow accumulation and the first snow-free day indicate that improvements are still needed in NWP products for precipitation and radiative fluxes. These are critical products for operational sea ice services, in particular for low solar height angles. Negative shortwave radiation bias has been found for HIRLAM in nearly clear-sky conditions with a low solar elevation(Rontu et al., 2017). Over the Baltic Sea, differences between the observed and HIRLAM-based

Q

were generally larger in conditions of a low solar height angle(Pirazzini et al., 2006).

The evolutions of snow and ice mass balance along the Tara drift trajectory and a parallel one 100 km north-west of it showed highly correlated mass balance patterns. The differences of modelled snow depth and ice thickness were much less than the differences caused by the effect of uncertainties of the meteorological forcing variables(Section 3.3) or caused by model experiments using a different initial snow depth and ice thickness or spatial variability within a very small footprint of about a few 10 m due to irregular distribution and re-distribution of snow observed at different places in the Arctic Ocean (Gerland and Haas, 2011). The reasons for the small differences probably include the following: (1) the seasonal mean weather conditions were almost the same along both trajectories, despite of instantaneous differences, and (2) the thermal inertia of snow and ice prevent large spatial changes of snow and ice thickness in response to the instantaneous differences of atmosphere variables. The spatial variations of snow and ice mass balance are,however, sensitive to differences in the initial snow and ice conditions and timing of major weather events, such as storms (Merkouriadi et al., 2017). From the perspective of seasonal sea ice forecast in the Arctic, the initial ice conditions and timing of the calculation are critical (Day et al., 2014). The often-observed large spatial variations of snow and ice thickness distribution (Haas et al., 2017) are,therefore, most likely dominated by the dynamic features of the sea ice. In the case of this thermodynamic study over the central Arctic Ocean far from the coasts, the horizontal resolution of atmospheric forcing fields would have not been of primary importance. However, horizontal gradients in atmospheric variables are usually much larger in coastal and archipelago regions, where a high model resolution is needed (Kilpeläinen et al., 2011). Also, modelling of small-scale sea ice dynamics, such as deformation and opening and closing of leads, is sensitive to horizontal resolution of atmospheric forcing (Itkin et al., 2017).

To improve our understanding of snow and ice characteristics in the Arctic Ocean, new observations from IMB are important (Gerland et al., 2019). Use of new satellite remote sensing products deliver promising results,as such from the ICESat-2 laser altimeter with valuable additional information on Arctic sea ice mass balance over larger areas (Petty et al., 2020; Koo et al., 2021). Using those in combination with

in situ

observations and modelling as presented in this study can lead to a further improved understanding of the Arctic sea ice mass balance and its changes.

A lot of new data were collected during the MOSAiC campaign in 2019-2020 (Krumpen et al., 2020; Lei et al.,2021). New findings are expected from further MOSAiC data analysis and forthcoming Chinese National Arctic Research Expedition (CHINARE) data analyses and modelling.

Acknowledgements

This study was initialized during DAMOCLES project (Grant no. 18509), which was funded by the 6th Framework Programme of the European Commission. The initial data analysis was funded by the Research Council of Norway’s AMORA project (Grant no.# 193592). The modelling work has been supported by the Academy of Finland (Contract 317999). The finalization of this work was supported by the European Union’s Horizon 2020 research and innovation programme(Grant no. 727890 - INTAROS). We appreciate two anonymous reviewers,and Guest Editor Dr. Ruibo Lei for their constructive comments that have further improved the manuscript.