长波传播时延特性及差分授时可行性分析

燕保荣 李 云 郭 伟 华 宇

(中国科学院国家授时中心，中国科学院精密导航定位与定时技术重点实验室，陕西西安 710600)

1 引 言

近年来，卫星导航系统的缺陷日益突出，给国民经济和国家安全带来极大的威胁。长波授时系统以其极强的抗干扰性能和较稳定的信号特征成为卫星导航系统补充和备份的最佳选择。利用长波信号进行定位和授时，需要确定长波发播台到用户接收机位置处的长波信号传播时延。然而，长波信号的传播时延值极易受到传播路径上温度湿度等气象条件、地面的电参数以及地形等实时因素的影响，使得长波传播时延难以精确预测，从而影响了长波系统定位和授时的精度。其中，气象因素和地面的电参数等实时因素无法用准确的模型进行预测，只能通过实际测量的长波传播时延来分析这些因素的实时影响。同时，地形起伏的影响虽然不会随时间变化，但是却包含在信号的传播时延中。考虑到这些影响因素在一定的空间范围内具有缓慢变化的特点，理论预测这些因素对邻近测试点的长波传播时延具有相似的影响。鉴于此，本文利用邻近区域内两点的实测结果分析邻近点上长波传播时延的变化特征。在此基础上利用Kalman滤波方法抑制测试数据中的随机噪声并计算两测试数据相关性，用于差分授时可行性的分析。

2 测试及分析方法

长波传播时延就是信号由发射天线发出并沿地面传播，在到达接收天线之前所经历的时间延迟量。在授时精度不高的情况下，可以利用长波信号传播时延的预测模型计算长波信号的传播时延。但是，由于预测模型采用了一定的近似处理，难以满足高精度的授时定位需求。为获得精确的传播时延值，最直接的方法就是在用户点上复现出长波发播台的标准时间，进一步测量接收的信号与标准信号的时延差。在用户点上复现标准时间可以采用搬运原子钟法，也可以采用相对测试法。原子钟搬运方法非常复杂，且容易受条件限制，在实际中多采用相对测试法。相对测试法以卫星系统的时间为中间量，实现用户点上标准时间的复现。下面介绍实际的测试过程以及对测试结果的分析方法。

2.1 测试过程

以GPS接收机为例，说明长波时延的精确测量原理以及过程，测量基本原理如图1所示。首先，在长波发播台位置处测量GPS接收机输出的1PPS秒信号与发播台标准时间UTC(NTSC)的1PPS秒信号之间的时间偏差，记为：

Δt

；其次，在用户点处以GPS接收机输出的1PPS秒信号作为参考，测量长波接收机接收的秒信号与参考时间之间的时延差，记为

N

，进一步计算转化为长波的传播时延。在统一的时间轴上满足式(1)

Δt

+

N

=

T

+

T

+

T

(1)

利用式(1)可以获得精确的传播时延值为

T

=(

Δt

+

N

)-

T

-

T

(2)

式中：

T

——长波授时台的标准脉冲1PPS与标准时间UTC(NTSC)的1PPS的时间偏差，其大小取决于长波授时系统对定时信号发射时的控制精度，可以通过电流回路进行精确测量，在理论上为已知值；

T

——长波信号从发播台发射天线到用户接收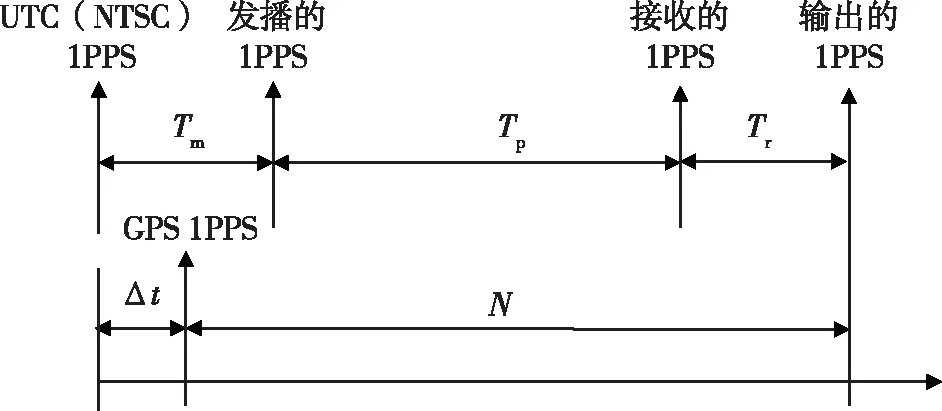

图1 相对测试法基本原理图Fig.1 The principle of relative test method

机天线的传输时间，即传播时延；

T

——长波信号在用户接收系统内的时间延迟，包括接收天线、耦合器、电缆和接收机通道对接收信号的总延迟，可以通过标校获得。

为分析差分授时方法的可行性，需要同时在两点进行传播时延的精确测试，两测试点所需的设备相同，都使用GPS接收机，长波接收机以及斯坦福的SR620计数器进行测试，测试过程的实物连接关系如图2所示。A点表示长波发播台，B点和C点表示两个测试点。

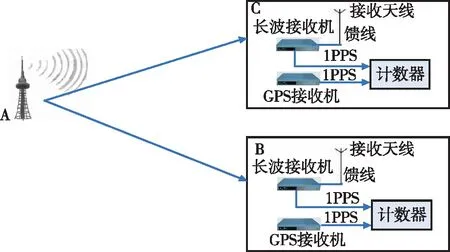
图2 测试设备连接图Fig.2 Diagram of test equipment connection

2.2 分析方法

相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。其定义公式为

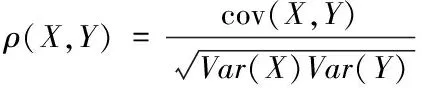
(3)

式中：

ρ

——相关系数；

X

,

Y

——两个测量序列；cov(

X

,

Y

)——序列

X

与序列

Y

的协方差；

Var

(

X

)——

X

的方差；

Var

(

Y

)——

Y

的方差。当序列的长度为

n

时，协方差的计算公式为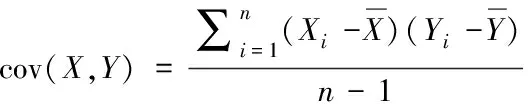

(4)

当|

ρ

(

X

,

Y

)|=0，表示两测量序列无线性相关关系，当|

ρ

(

X

,

Y

)|<0

.

4，两序列为低度线性相关，当0

.

4≤|

ρ

(

X

,

Y

)|<0

.

7，为显著性相关，当0

.

7≤|

ρ

(

X

,

Y

)|<1，为高度线性相关。利用相关关系分析两测试点上传播时延的变化情况，可以证明两条传播路径上的时延影响因素的相关性，也可以说明两条传播路径上的空间相关性。

需要说明的是：长波接收机在测量数据时，不可避免的存在随机噪声，由于测量值中的随机噪声之间无相关性，需要对采集的测量值进行滤波处理，消除随机噪声的影响，再计算相关系数。因此，首先需要考虑采集数据随机噪声的处理。本文采用Kalman滤波的方法对随机噪声进行抑制，该方法以最小均方误差作为估计的最佳准则，适合于数据的实时处理。

3 长波传播时延及相关性

我国的长波发播台位于陕西省蒲城县，为验证气象因素、地面电参数以及地形等因素对长波传播时延的影响，在一定的区域范围内选择两点同时进行静态测试。由于两测试点同时进行，需要对两测试点的GPS参考接收机以及长波接收机进行标校处理，以消除两参考接收机之间的固有误差。选择近距离和中远距离范围内的两个试验区域进行测试，测试设备连接图如图2所示。近距离区域选在西安，中远距离区域选择在榆林。选择的两试验区域与长波发播台的位置关系如图3所示。其中，临潼和西安两测试点位于蒲城发播台的西南方向，坐标分别为(109°13.33′E，34°22.11′N)和(108°59.71′E，34°8.44′N)，如图3(a)，临潼点距离发播台的大地线距离为71.163km，西安点距离发播台的大地线距离为103.227km，并且两测试点的大地线距离约为32.812km，结合地形图可知，由发播台到两测试点的地形较为平坦，并且两地相距较近，气象条件及地形条件都很相近。另外两测试点选择在榆林和红碱淖，位于发播台的东北方向，坐标分别为(109°45.02′E，38°15.02′N)和(109°56.31′E，39°2.92′N)，如图3(b)，榆林测试点距离发播台的大地线距离为366.904km，红碱淖测试点距离发播台的大地线距离为474.970km，并且两测试点的大地线距离约为108.366km，结合地形图可知，两条传播路径上的地貌环境、气象条件也非常相似，即介电常数及等效电导率、气象变化等都近似相同。

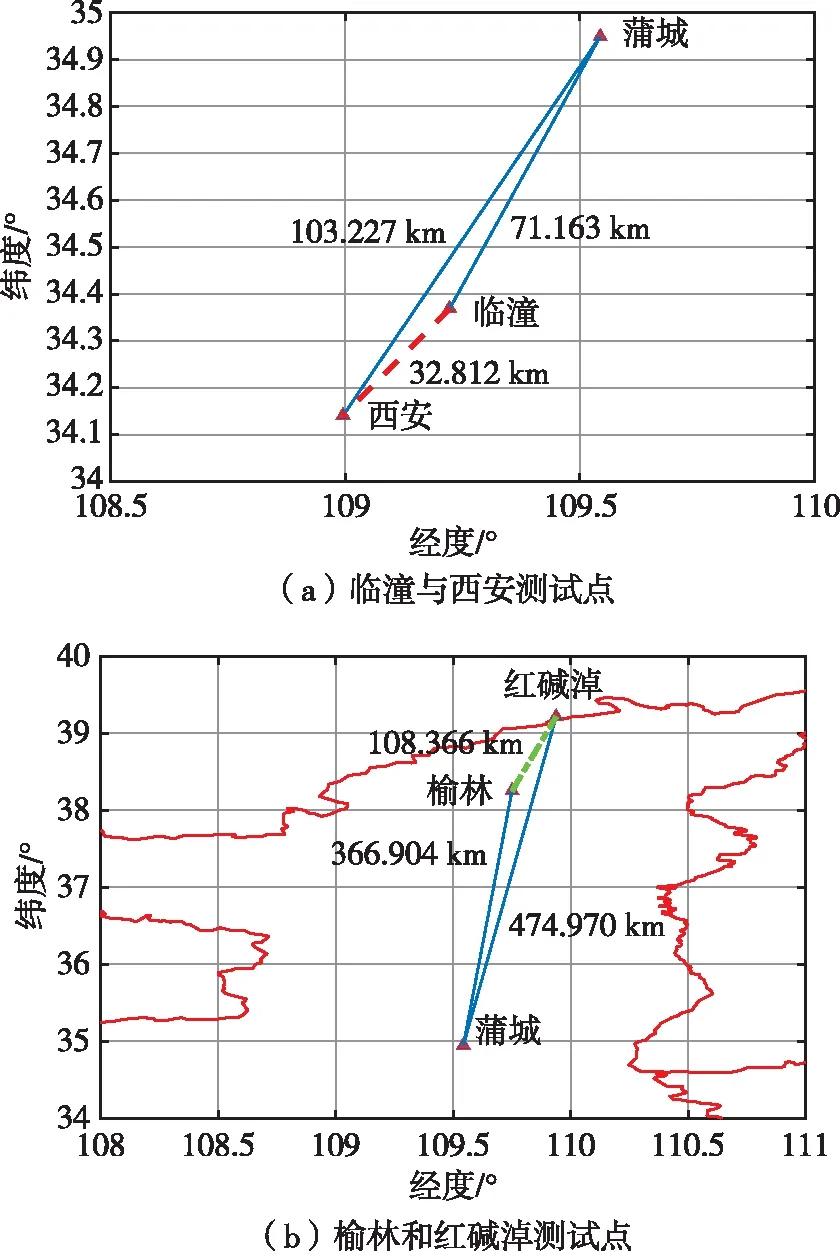
图3 试验区域与发播台的位置关系示意图Fig.3 Location relationship between test area and transmitter station at Lintong,Xi’an,Yulin and Hongjiannao

3.1 长波传播时延特性

利用测试点的测试结果分析长波传播时延的变化特性，两测试区域一天内的测试结果如图4所示，测量量表示为

N

。这里未考虑

Δt

、

T

和

T

等因素的影响，并按照3

σ

准则剔除了测试数据的粗大值。图4(a)为临潼和西安两点的测试结果，测试时间内临潼点计算的平均值为：345.170μs，标准差(Standard deviation，STD)为：18.780ns，西安测试点的均值为：453.032μs，标准差为：22.864ns。图4(b)为榆林和红碱淖两点的测试结果，两点的均值分别为，1 253.157μs和1 552.538μs，标准差分别为14.505ns和19.199ns。从上面两个测试区域的测试结果可以看出：测量数据中包含了随机噪声，在一天的时间跨度内，测量值随着时间的变化具有一定的波动性，最大值出现在12h之后。这是因为传播路径上空气折射指数受温度、湿度等因素的影响，同时，温度和湿度也会影响地面等效介电常数等因素，从而引起长波信号二次时延的变化，这些变化最终都会体现在接收机测量的传播时延中。测试结果表明，传播路径时延是随时间缓慢变化的，在传播路径相似的情况下，传播路径时延随时间的变化趋势也较相似。这种相似的变化趋势表明传播路径上的影响因素是相关的，具有一定的时间空间相关性。

图4 时延测试结果波形图Fig.4 Measured result of propagation delay at Lintong,Xi’an,Yulin and Hongjiannao

3.2 相关性分析

利用2.2节描述的相关系数的计算方法计算上面两个试验点的相关系数，用于分析传播路径上各种影响因素的相关性。由于测试数据中包含了随机噪声，并且随机噪声之间无相关性，因此，需要对采样数据进行滤波处理。Kalman滤波方法对数据的长度无要求，本文采用该方法对测试数据进行预处理。

测量噪声的协方差通常取为测量值的标准偏差，记为

R

，过程噪声的协方差表示为

R

，然后计算两测试点上滤波结果的相关性。过程噪声是控制滤波效果的一个重要量，当测量噪声的协方差恒定时，过程噪声的值越大滤波效果越明显。

R

/R

取不同数值时两测试区域两个测试点滤波后的相关系数(图中蓝色线)以及测试点滤波残差的标准差(图中虚线和橙色线)如图5所示，图5(a)表示西安地区的测试结果，图5(b)表示榆林地区的测试结果。从图中可以看出，随着

R

/R

值的增加，两测试数据的相关系数也随之增加，当

R

/R

>10时，相关系数大于0.7，表示两者具有高度相关性。当

R

/R

的值增加到一定程度，相关系数可达1，但是，测试数据中的低频量也将被滤除。同时，滤波残差的标准偏差随着

R

/R

值的增加也会出现变化，在10～10之间，残差标准偏差近似维持相同的数值，说明在该取值范围内滤波效果近似相同。

图5 相关系数及滤波残差的标准差曲线图Fig.5 Correlation coefficient and the standard deviation of filtering residual error

选择

R

/R

=10的值，对两测试地区的数据进行滤波处理，滤波后曲线如图6所示。其中，西安地区临潼点滤波后最大值与最小值的差为：43.131ns，西安点滤波后最大值与最小值的差为43.570ns，滤波后的相关系数为0.871；榆林地区两测试点滤波后，最大值与最小值的差分别为43.058ns和50.270ns，滤波后的相关系数为0.897。通过滤波后相关系数的分析，相距不远的两点具有较强的相关性，即传播时延随时间的变化趋势近似相同。在一天的时间跨度内，波动范围基本不超过60ns。为分析Kalman方法对随机噪声的滤波效果，对滤波残差进行统计分析，西安地区两测试点滤波后的残差分别为：15.058ns和18.707ns，榆林地区两测试点滤波后残差分别为：10.2ns和13.7ns。滤波残差分布符合高斯分布，如图7所示。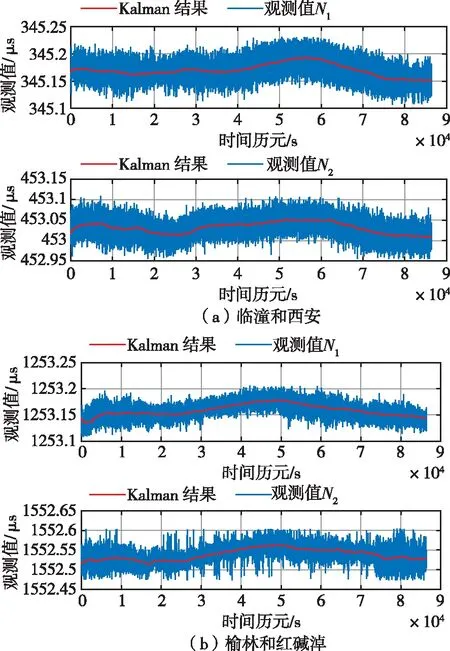

图6 测量结果和滤波结果波形图Fig.6 Measurement results and filtering results at Lintong,Xi’an,Yulin and Hongjiannao

图7 Kalman滤波后是残余误差统计图Fig.7 Residual statistics after Kalman filtering at Lintong,Xi’an,Yulin and Hongjiannao

上述分析都是基于测量的精确传播时延进行的，但是在实际应用中，用户点并不能严格复现标准信号，因此基于传播时延的变化特点，可以选择一点作为参考点，并在该点复现标准参考信号，实时测量出该点的传播时延，包含传播路径上时延的变化特性，并计算该点的时延波动值作为差分改正数，用于附近区域的时延修正，可以有效的抑制/削弱传播时延随时间变化的波动。

4 结束语

通过对长波传播时延精确测量值的分析可知，Kalman滤波后长波信号传播时延并不是恒定值，在一天的时段内会有波动，测试结果显示：一天内的波动值一般不超过60ns，这些波动并不是随机噪声的影响，而是由于传播路径上气象条件、传播介质的电参数等因素实时变化的结果；选择合适的滤波参数后，邻近测试点在相同的时间段内具有相似的变化趋势，滤波后计算的相关系数大于0.7，体现为高度的线性相关。Kalman滤波方法消除了随机噪声的影响，滤波残差符合高斯分布。综合上述分析可得：在一定的范围内，气象条件、传播介质的电参数、地形起伏等因素近似相同，实时变化对传播时延的影响也相似，使得长波传播的时延具有一定的时间空间相关性。为提高长波的授时精度，可以利用差分以及滤波方法消除传播路径上的实时波动及噪声影响。