《用列举法求概率（树状图）》教学实录与评析

张宝丹 刘小红

用列举法求概率（树状图）是人教版数学九年级上册第25章第2节第3课时内容.学生学习这一内容之前已经了解随机事件、概率等概念，知道用列表法求概率.本节课学习用树状图法求概率，教学伊始从学生熟悉的情景切入，然后引导学生自主探究、合作交流，让学生掌握用树状图求概率的方法，解决实际问题，培养学生分析问题和解决较复杂问题的能力.

一、创设情境，激发兴趣

师：请同学们观看小视频.（播放动画视频：小丁和哥哥去上学，过马路遇到红绿灯，能够做到遵守交通规则）看完视频，你发现了什么？

生1：小丁和哥哥看见红灯就停下，看见绿灯就向前走.

生2：小丁和哥哥遵守交通规则.

生3：小丁和哥哥上学要经过两个十字路口，每个路口遇到红灯和绿灯的机会相同，求小丁和哥哥上学时经过每个路口都是绿灯的概率.

师：同学们观察得真仔细！那么，概率是多少呢？

生：[1/4].

师：你是怎么知道的？

生：用列表法计算.

师：你是怎么想到用列表法计算的呢？

生：当一次试验涉及两个因素，并且可能出现的结果数目较多时，为了不重不漏地列出所有可能的结果，通常采用列表法.

师：说得好！你还想到求概率的其他方法吗？

生：用树状图法.

师：对。这节课我们学习用树状图法求概率.

【评析】教师播放动画视频，激发了学生的探究兴趣，同时引导学生回顾和梳理所学知识，为学习新知奠定基础.

二、合作探究，发现新知

师：请同学们看导学案中的“探究一”.

课件演示：小丁上学要经过三个十字路口，每个路口遇到红灯和绿灯的机会都相同，求小丁上学时经过每个十字路口都是绿灯的概率，能用列表法解决吗？如果不能，你还有什么方法？

生分小组进行交流.

生：由题目可知，小丁上学要经过三个十字路口，经过每个十字路口都会遇到红灯、绿灯这两种情况，所以，共有八种情况，而每个十字路口遇到红灯和绿灯的机会都相同，由图1可知，他经过每个路口都是绿灯的情况占八种情况当中的一种，因此，概率是[1/8].

师：其余同学有补充吗？

生：（补充）书写格式不规范，首先要写“解：依题意可知”，最后要写“共有8种可能的结果”.

师：这名同学的建议非常好！解题格式要规范.这个小组先进行分类，然后通过图形把所有可能的结果都表示出来，体现了数形结合的数学思想.仔细观察图形，你觉得它像什么？

生：像一棵倒着长的树.

师：是的.这种解题的方法我们把它叫作树状图法.那么，什么时候用树状图法计算概率呢？

生：当一次实验涉及三个或三个以上因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法.

师：想一想，我们怎样画出树状图？

生：实验中涉及三个因素，第一个因素中有两种可能的情况，第二个因素中各有两种可能的情况，第三个因素中各有两种可能的情况，这样就可以画出一棵倒着长的树.

【评析】教师通过变式，把实验中的两个因素变为三个因素，学生发现用列表法难以解决这个问题，从而引发思考，在小组合作学习中寻找新的解决方法——树状图法.

三、学以致用，深入理解

师：请同学们看导学案中的“探究二”.

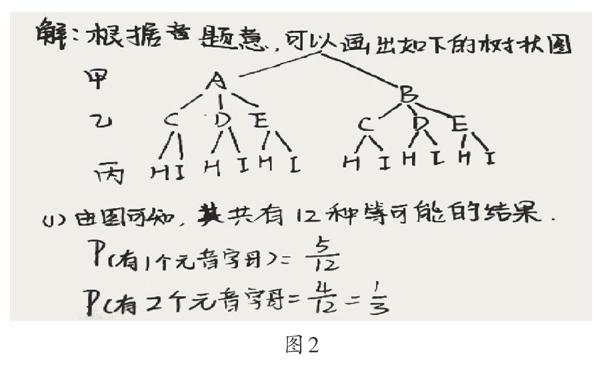
课件演示：甲、乙、丙三个盒子中分别装有大小、形状相同的卡片若干.甲盒中装有两张卡片，分别写有字母A、B;乙盒中装有三张卡片，分别写有字母C、D、E;丙盒中装有两张卡片，分别写有字母H、I.要从三个盒子中各随机取出一张卡片，求：（1）取出的三张卡片中恰好有一个，两个，三个写有元音字母的概率各是多少？（2）取出的三张卡片全是辅音字母的概率是多少？

生思考交流，师巡堂指导.

师：下面请小组来展示你们的学习成果.

生：二十六个英文字母中，元音字母有a、e、i、o、u，其余都是辅音字母.由题目可知，有甲、乙、丙三个盒子，也就是三个因素，可以用树状图解决问题.甲盒中的两张卡片分别写着字母A、B，乙盒中的三张卡片分别写着C、D、E，那么就有六种情况;丙盒中有两张卡片，有可能抽到H，也有可能抽到I，加起来共有12种可能的结果.其中带有一个元音字母的有ACH，ADH，BCI，BDI，BEH，所以，取出带有一个元音字母的概率是[5/12];依此类推，带有两个元音字母的概率是[4/12]，化简后是[1/3];取出的卡片中有三个元音字母的概率是[1/12]（如图2）.

生：（补充）三张卡片上全是辅音字母的有BCH、BDH两种，全是輔音字母的概率是[2/12]，化简后是[1/6].

师：这个小组在展示说明时思路清晰，语言流畅.同学们想一想，列表法和树状图法的优点分别是什么？

生：用树状图法或列表法计算概率，可以清晰地表示出某个事件发生的所有可能出现的结果，能够比较方便地求出事件发生的概率，这是最直观最常用的计算方法.

师：它们的区别又是什么呢？

生：当实验包含两个因素时，两种方法都可以用，当实验中涉及三个或三个以上因素时，用树状图法比较方便.

【评析】抽卡片是学生熟悉的游戏，教师引导学生用树状图法解决问题，能够帮助学生更好地理解和掌握用树状图求概率的方法.教师适时的追问，有利于学生明确这两种求概率方法的优劣，在解决实际问题时选择合适的方法.

四、巩固提升，解决问题

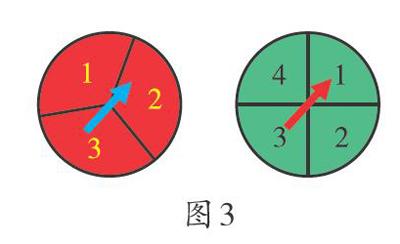
师：学校要举行元旦晚会.为了活跃气氛，组织者设计了一个转盘游戏，游戏中的两个圆盘分别被等分成三个扇形和四个扇形（如图3）.小明和小亮玩转盘游戏，他们同时转动两个圆盘，指针停止后指向区域得到两个数字.若两个数的乘积为奇数，则小明胜;若两个数的乘积为偶数，则小亮胜.你认为这个游戏公平吗？请说明理由.

生1：这个游戏不公平。第一个转盘有三个因素，第二个圆盘有四个因素，可以求出共有12种可能的结果，计算它们的乘积，两数乘积为奇数一共有1，3，3，9四种可能，概率是[4/12]，化简后是[1/3]，而两数乘积为偶数一共有八种可能，概率是[8/12]，化简后是[2/3]，所以，小亮获胜的概率大于小明（如图4）.

生2：我用列表法计算。根据题意，先把第一个转盘的三个因素写成一列1，2，3，第二个转盘的四个因素写成一行1，2，3，4，然后罗列出12种可能的结果（如图5）.后面的做法和前面的同学一样，小亮获胜的概率大于小明.

师：这个小组做到了一题多解.游戏是否公平，关键要看什么？

生：看概率是否相等，如果概率相等，游戏是公平的，反之则不公平.

【评析】通过分析转盘游戏公平与否的问题，学生想到了一题多解，无形中巩固了列表法和树状图法的知识，明确游戏是否公平与概率有关.

师：既然这个游戏不公平，你能为他们设计一款公平的游戏吗？

生独立思考后交流.

生1：若两数之和为奇数，则小明胜;若两数之和为偶数，则小亮胜.我用列表法展示给大家看.第一行分别是2，3，4，5，第二行分别是3，4，5，6，第三行分别是4，5，6，7，这些结果每一种出现的可能性都相等，所有的可能结果一共有12种，两数之和为奇数的情况共有6种，所以，两数之和为奇数的概率是[1/2].同理，两数之和为偶数的概率也是[1/2]，二者的概率相等.因此，这样设计游戏是公平的.

生2：若两数乘积大于4，则小亮胜;若两数乘积小于4，则小明胜.我用树状图法解决这个问题（如图6）.先求出每一种结果的两数乘积，可以看出乘积大于4的有5种情况，概率为[5/12]，乘积小于4的概率也是[5/12]，所以，两数乘积大于4和小于4的概率相等，因此，游戏是公平的.

生3：我还有一个方案，把第一个圆盘的数字看成十位数，把第二个圆盘上的数字看成个位数，由此组成两位数，如果是奇数，则小明胜;如果是偶数，则小亮胜.把这些所有的可能列在一个表格当中，这些数分别是11，21，31，12，22，32，13，23，33，14，24，34，共有12种可能的结果.组成的两位数为奇数的概率为[6/12]，即[1/2]，组成的两位数为偶数的概率为[6/12]，化简后是[1/2]，二者的概率相等，按照规则，游戏是公平的.

师：同学们设计了多种不同的方案，想法非常好！老师发现还有同学设计了不同的方案，因为时间有限，所以不能逐一展示，课后同学们可以相互交流你们的方案.

【评析】请学生设计游戏方案，为学生提供问题解决的平台，这是教学的亮点.教师这样做，有利于学生巩固所学知识，开阔思路，体现了课堂教学的深度与广度.

五、梳理反思，感悟收获

师：我们来小结本节课学习的内容，说一说你有什么收获？你会提出什么建议？你还有哪些困惑？

生1：列表法、树状图法都适用于涉及两个因素的试验，但是实验中涉及三个或三个以上因素时，用列表法不太方便，为了不重不漏地列出所有可能的结果，通常采用树状图法.

生2：我学会了分类和数形结合的方法.

生3：我知道如何判断游戏是否公平.

生4：如果实验中的因素再多几个，还能用树状图法计算概率吗？有没有其他方法求概率？

师：求概率的方法有很多，上了高中还要学习，同学们有兴趣的话继续探究.

【评析】教师引導学生回顾和梳理学习内容，谈收获，有利于学生巩固所学知识，掌握学习方法，将课内学习延伸至课外.

【总评】这是一节有梯度、有深度、有宽度的课，体现在三个方面：首先，教师从学生熟悉的红绿灯、摸卡片、玩转盘等情景切入教学，使学生积极投入学习活动当中，并在轻松愉悦的氛围中畅所欲言，培养了学生学习的主动性和创造性.其次，学生自主探究、合作交流，大胆展示学习成果，分享自己的想法和感悟，教师及时反馈回应，适当引导，适时鼓励，为学生顺利完成探究任务注入了“润滑剂”，课堂教学高潮迭起，精彩纷呈.最后，学生经历了探究、发现、创造的过程，体现了知识的产生、发展和应用的过程，触及数学知识的本质，体会到了数学中所蕴含的思想方法，是一节指向学科素养发展的课.

（本文所用课例获2019年贺州市“一师一优课，一课一名师”活动优课一等奖）

（责编 欧孔群）