极化码基于比特翻转改进的BP译码算法

王华华，秦 红，方泽圣，李平安，陈 博

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

由Arikan E提出的极化码是世界上第一种能够被严格证明香农门限可达的编码方案[1]。同时，Arikan E还提出了两种针对极化码的译码算法，分别是连续消除(Successive Cancellation,SC)[1]和置信传播(Belief Propagation,BP)译码算法[2]。

SC译码算法及其衍生的算法，如SC翻转(SC Flip,SCF)[3]和列表SC(SC List,SCL)译码算法[4-5]已成为大多数人的关注点。与之相反的是BP译码算法[6]，与串行SC译码算法相比，BP译码算法通过并行迭代计算，在高吞吐量的应用场景中具有更大的优势。然而，BP译码算法的性能不如SCL译码算法，因此，在文献[7]中，作者提出了一个固定的临界集作为翻转集的译码方法，即BP比特翻转(Bit-Flip,BF) (BPF)译码，通过对数似然比(Log-Likelihood-Ratios, LLR)的值来选择错误概率更大的比特进行翻转，由此来达到提升译码性能的目的，然而这种算法会因为翻转集的不准确而导致译码性能的提升有限；此外，在文献[8]中，一种增强型BPF(Enhanced BPF,EBPF)译码算法被提出，它通过减少不可靠比特的范围从而降低译码复杂度，并且具有比文献[7]更高的译码性能。

本文提出了一种构建翻转集的新方法，先用文献[9-10]中所描述的方差方法基于LLR的BPF(BPF-LLR)译码算法来构建粗翻转集FS，再使用误码率(Bit Error Rate,BER)的差值构建精翻转集FS′，从而实现了BER-BPF译码算法(BER-BPF-ω，ω为阶数，单比特时ω=1)。仿真结果表明，新算法降低了译码迭代次数，且性能较文献[8]和[10]有很大提升。

1 极化码基本原理

极化码的设计核心理念便是对信道进行极化处理，在这个过程中使得一部分信道的容量趋近于1，而另一部分信道容量趋近于0。信道极化包含两个过程：信道联合和信道分裂。

1.1 信道极化

信道联合：对已知的二进制离散无记忆信道W进行N次复制WN：XN→YN(式中：X和Y分别为输入和输出矩阵；N必须为2的整数次幂。)，并对复制所得信道进行信道组合。其中WN为信道联合前的原始信道，信道联合后的复合信道为WN，其转移概率为

1.2 极化码编码

极化码编码一般有3个过程，一是对极化信道可靠性的估计；二是进行比特混合；三是构造生成矩阵。

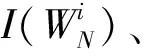
2 极化码的译码

2.1 BP译码算法

BP译码算法相比其他译码算法的一个最大特点是可以并行译码，由此可提高译码速度，其主要通过因子图的左右循环迭代来实现译码。图1所示为N=8时的BP译码因子图，其中红色部分为一个长度为2的极化码因子图的运算过程，其计算过程为

式中：L和R分别为从右到左和从左到右的LLR值。g(s,t)为

式中，s、t∈R。

BP与SC译码算法的很大区别就在于BP译码算法需要经过多次迭代最终得出LLR值。如图1所示，红色部分箭头方向向左迭代算半次迭代，向右迭代也算半次迭代，两者合二为一便为一次迭代，本文中统一将迭代次数M设置为200。当迭代完成后将左边的LLR值经式(7)得出最终译码结果：

图1 N=8时的BP译码因子图

2.2 BPF译码算法

极化码中的BF译码最早被应用于单个BF的SC译码，被称之为SCF译码。在单比特译码之后，SCF译码器将译码中出错率最高的非冻结比特收集并建立了一个大小为T的翻转集，且最多翻转次数为T。在极化码传输过程中，出现译码错误的主要原因便是差错传播，通过翻转第一个错误，能够提升译码的性能。但翻转集的最大缺陷在于，如果没有找到第一个错误的比特，那么性能几乎不会有提升，而且大多数时候，错误比特不止一个，所以单BF对译码性能提升有限。

BPF译码算法的译码流程如图2所示，其基本步骤如下：

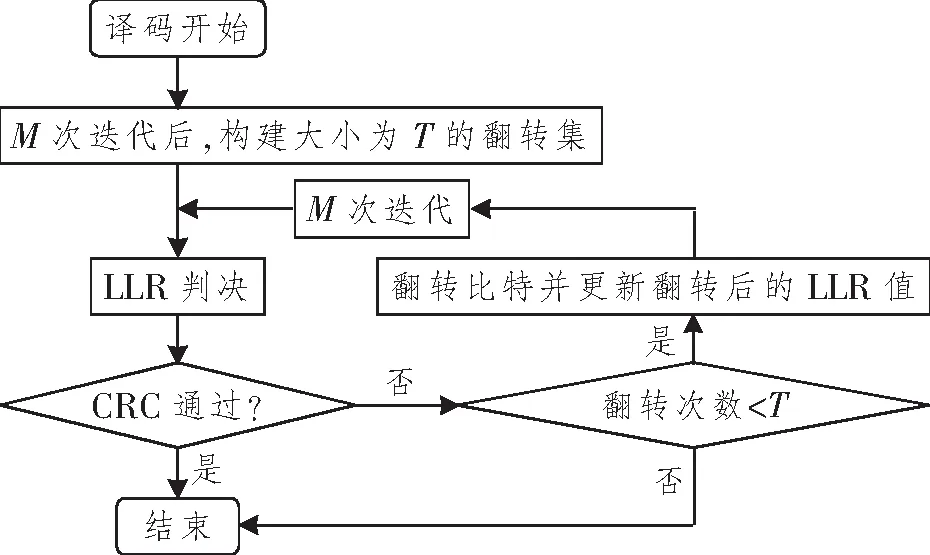
图2 单BPF译码流程图

(1) 进行普通BP译码，所有非冻结比特的先验LLR设置为0；

(2) 若达到最大迭代次数M，选出不可靠信息比特，构建一个大小为T的翻转集；

(3) 对LLR信息进行判决，然后进行循环冗余校验(Cyclic Redundancy Check， CRC)；

(4) 若CRC正确，则结束译码，否则判断翻转次数是否

(5) 将不可靠信息比特ui进行翻转，将ui<0的LLR设置为-∞，反之则为+∞，即LLRui=(1-2ui)×∞；

(6) 对更新后的LLR值进行BP译码，若达到M次迭代则进入第(3)步。

在上述步骤(2)中，如何选择出不可靠信息比特，构建出正确的翻转集是最大的难点，在文献[9]中，作者提出了利用因子图最左端连续S个LLR迭代信息的方差来选择出最不稳定的T个点。由于一个数据的方差可以显示出该数据的稳定性，所以如果某个数据的似然比信息方差越大，那么其稳定性越差，即为不可靠点。首先将每个比特的连续S个左信息求均值AVE_S，然后根据均值求出每个比特的方差VAE_S，计算公式为

3 BER-BPF-ω译码算法

文献[9]中所提算法为了降低最终迭代次数，对翻转集的大小进行了约束，使得部分错误比特并未进入到翻转集中，最终性能提升有限。所以本文提出了BER-BPF-ω译码算法，它可以更准确地找出不可靠点。相比文献[9]，本文所提算法迭代次数有所下降且性能明显提升。本文所提算法借鉴了文献[9]中的方差确定翻转集的方法，但与之不同的是扩大了翻转集的大小T，同时还使用了一种新的方法来缩小翻转集的大小再进行多比特翻转。

假设本文中所有码字经BPSK调制并在高斯信道中传输。那么码字x经过调制传输后，接收到的y所对应的LLR值为

式中，φ(x)为

因此，我们可以根据文献[11]得到码字通过高斯信道的BER为

式中：PE为经高斯信道后得到的估计值；erfc()为互补误差函数，与此同时，我们可以得出经过BP译码后信息比特的BER为

(1) 进行普通BP译码，所有非冻结比特的先验LLR设置为0；

(2) 根据式(5)从右向左依次更新每一列的左信息，直到最左边；再反方向更新至最右侧；

(3) 对步骤(2)进行M(此处M取值为50)次迭代操作，同时记录迭代结束前S(此处S取值20)次的左信息值，并计算其平均值AVE_S以及方差VAE_S；

(4) 由式(7)得出译码后的ui，并对所得结果做CRC校验，若未通过，则选取VAE_S最大的T(此处T取值为信息比特的1/2)个值构建粗翻转集FS；

(5) 将FS的T个比特进行BER计算，再比较PE与PBP的大小，构建精翻转集FS′={i∈A|PBP(i)>PE(i)}(A为信息比特索引集合)，大小为T′，并以BER差值的降序排列；

(6) 先对精翻转集FS′做单BPF译码，其基本步骤如2.2节所示，如果最终所有CRC均未通过，则进行多BPF译码，将翻转集FS′中的比特以ω个组合形成新的翻转集FS″，ω按顺序依次递增，直到CRC校验通过或者ω>T′。

4 结果与分析

本节中，在AWGN信道下，采用的调制方式为BPSK，对提出的BER-BPF-ω译码算法仿真结果进行分析。

为了验证本文所提算法的可行性，分别对256和1 024码长进行了仿真分析，同时也对BP、EBPF和BPF-LLR译码算法进行了仿真，用以对比验证本文所提算法的性能。图3(a)和3(b)所示分别为对(256,128)和(1 024,512)型极化码的BER仿真波形，由于本文的重心不在于翻转集的设定，故根据文献[9]将翻转集大小分别暂定为T=10和20，且CRC校验类型为CRC-16。

注：SNR为信噪比。 图3 两种码长时几种译码算法的BER

由图3可知，本文所提算法与BP、EBPF和BPF-LLR算法相比，其BER有明显提升，例如在BER为10-3时，图3(a)中分别约有0.495、0.175和0.280 dB的性能提升。同时，由图3 (b)可知，随着码长的增加，译码性能有更高的提升，在SNR=3 dB时，本文所提算法就可以达到完全译码。

表1所示为对上述几种算法迭代次数的统计，其中BP译码因为没有翻转过程，所以经过M次迭代后便会结束译码(M=50)。由表1可知，本文所提译码算法相比EBPF译码算法减少了约10%的迭代次数，相比BPF-LLR译码算法减少了约25%的迭代次数，由此可知，本文所提译码算法在迭代次数上有所降低。

表1 码长为256和1 024时不同SNR下的总迭代次数

通过对本文所提算法进行BER和复杂度的分析可知，本文所提算法优于现行的BPF译码算法，虽然复杂度降低不是特别明显，但其性能有很大提升。

5 结束语

本文所提BPF译码算法主要在于翻转集的构建，提出了粗翻转集和精翻转集的概念，通过数据的方差可以判断数据稳定性的特点来构建粗翻转集，再通过高斯信道后的BER与译码后的BER差值比较来构建精翻转集。在仿真分析中可以看出，本文所提译码算法在性能和复杂度上都有所提升。接下来的研究重点是将该算法通过硬件平台(如现场可编程门阵列(Field Programmable Gate Array，FPGA))实现。