Q345/SUS304异种钢焊接接头固有应变的变化规律研究

2021-08-16李元泰吴华鑫肖慎翀

中国机械工程 2021年15期

李元泰吴华鑫董斌肖慎翀

武汉第二船舶设计研究所，武汉，430064

0 引言

为满足高强度、耐腐蚀等复杂环境要求，大型异种钢焊接结构开始广泛应用[1-2]。异种钢焊接接头由于各自材料的热物理性能和力学性能之间存在显著差异，焊后变形分布相比同种材质接头更为复杂[3]。数值模拟作为焊接领域重要的研究方法，从20世纪开始一直被学者用来预测焊接结构的残余应力与变形。UEDA等[4]率先采用有限元法对焊接过程进行热弹塑性计算，分析了平板对接焊、角接焊的温度和应力分布。针对焊道长、焊缝多的大型结构，UEDA等[5]又提出了固有应变理论及计算方法来解决传统的热弹塑分析效率低下的问题。HUANG等[6]进行了SUS301不锈钢板的激光焊接试验，基于固有应变理论的弹性有限元法预测的焊接变形结果与试验结果吻合，并且非常高效。DENG等[7]运用固有应变方法计算了船舶大型加筋板结构的焊接变形。WANG等[8-9]通过数值模拟和试验的方法预测碳钢、不锈钢等结构的焊接变形，指出焊接变形的大小和分布与热输入、板材的厚度、材料、焊接接头型式密切相关。王林等[10]运用热弹塑性有限元法和固有应变法对离心叶轮风机的焊接工艺进行优化。以上大型单一金属材料构件焊接变形的快速预测比较成熟，但目前异种钢结构的焊接变形的研究主要基于试验和效率相对较低的热弹塑性分析方法[11-12]，快速预测异种钢焊接结构的变形报道较少。

本文以Q345钢和SUS304不锈钢平板对接接头和T型接头为研究对象，基于固有应变理论，利用异种钢焊接有限元模拟方法研究了固有应变的变化规律。

1 固有应变与焊接变形

1.1 弹性壳单元法

采用四节点壳单元模型有限元分析时，根据薄板大挠度弯曲理论，矩形薄板任意一点的应变-位移关系(忽略横向剪切应变的影响)可描述为

(1)

(2)

(3)

平行于oxz平面的曲率kx、平行于oyz平面的曲率ky、oxy平面的扭转曲率kxy分别为

(4)

弹性壳单元法的计算过程就是将已知的应变分量作为初始应变来计算变形的过程。

1.2 固有应变的转化

固有应变法的基本思路是：将6个固有应变值简化为横向固有应变、纵向固有应变和曲率3种固有应变；通过热弹塑性有限元法计算得到3种固有变形(横向收缩、纵向收缩和角变形)并通过转化得到3种固有应变，在壳单元模型中采用弹性壳单元法计算得到最终变形。

对于对接接头和T型接头焊接件，纵向收缩可通过收缩力FTendon[13]反映，其计算公式为

(5)

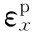
横向收缩同样也可以通过塑性应变积分计算，本文以对接接头为例，采用估算公式如下：

S=UyA-UyB

(6)

式中，S为横向收缩量；UyA、UyB分别为图1中的线A和线B各自在横向方向上的位移。

(a)平板对接焊的变形

角变形也可以通过下式反映：

(7)

式中，β为左右两侧的平均角变形；B为腹板的半宽；UZC、UZD为图1的中线C和边线D的挠度。

固有应变则可通过固有变形转化，其计算公式如下：

(8)

(9)

(10)

同理，对于T型接头，翼板和腹板的等效纵向固有应变可以根据COTTRELL[14]提出的分配比例计算得到，而横向固有应变与曲率的计算方法与对接接头的计算方法一致。

2 固有应变的变化规律分析

本文基于ABAQUS软件，提出了Q345/SUS304对接接头的热弹塑性有限元法，将数值模拟计算结果转化为固有应变数据，采用固有应变法计算最终变形结果。将热弹塑性模拟结果、固有应变法计算结果与试验结果进行对比，来验证该方法的准确性。以对接接头和T型接头为典型焊接接头模型，改变板厚、热输入条件，进行大量的数值模拟试验来研究它们与变形结果的关系，得到固有应变的变化规律。

2.1 典型接头的计算与验证

研究对象为Q345/SUS304异种钢平板对接接头，其试件尺寸为300 mm×300 mm×10 mm，采用MIG保护焊，填充材料为Y309L焊丝。焊接条件见文献[11]。数值模拟采用双椭球体积热源模型，热源有效功率系数为0.85，散热系数取10 W/(m2·s·K)。不考虑焊接填充材料与母材性能差异。热弹塑性分析过程中，两种材料随温度变化的热物理、热力学性能参数如图2所示。

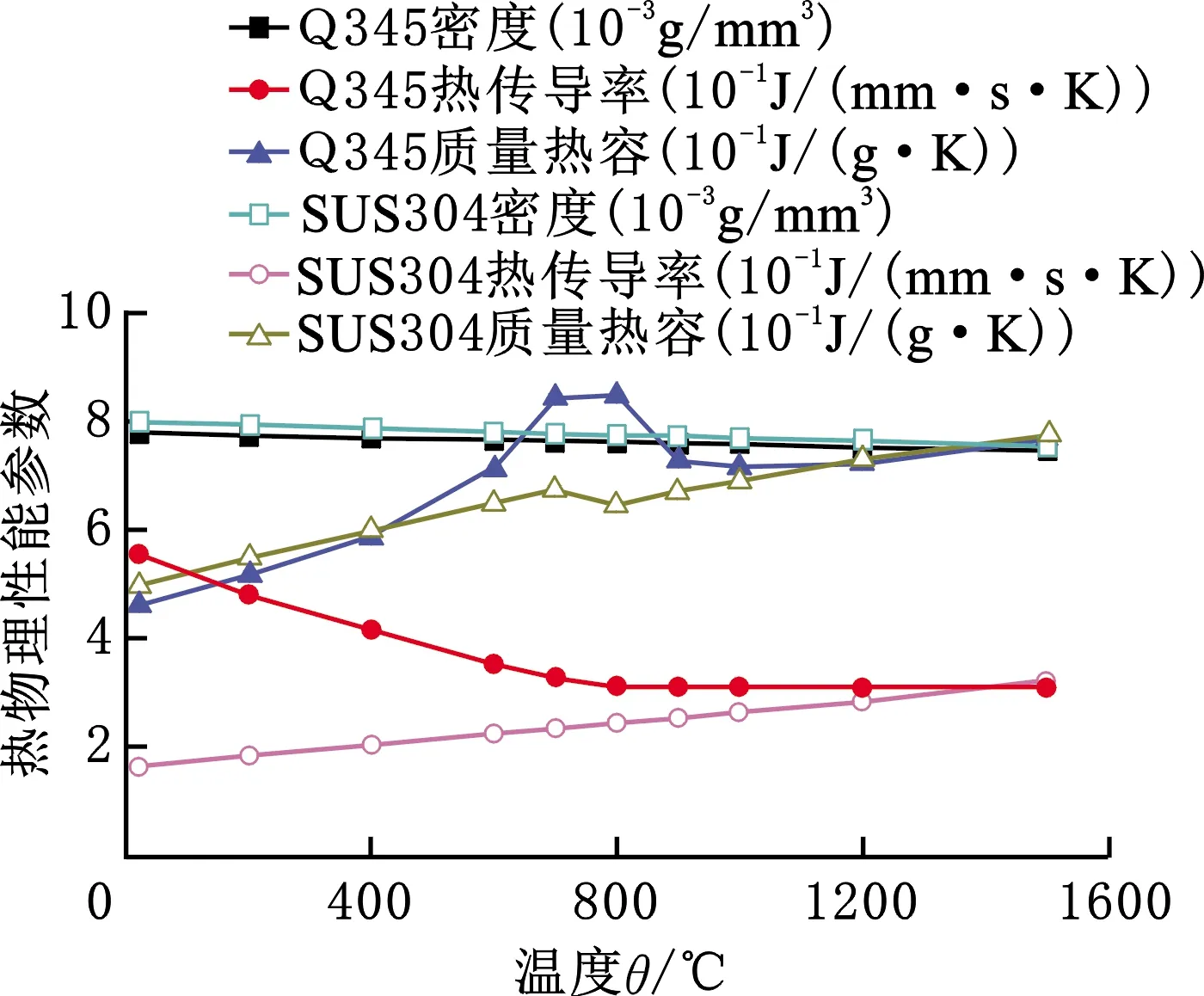
(a)热物理性能参数

Q345/SUS304对接接头进行热弹塑性计算后得到的焊接变形结果为：纵向收缩力432 kN，横向收缩量1.855 mm，角变形0.0663 rad。根据转化式(9)～式(10)求得固有应变，见表1，应用弹性壳单元法计算典型焊接接头的变形并与试验结果进行比较，其中，试验测量点位置和数值计算的测量路径示意图见图3。

表1 固有应变计算结果

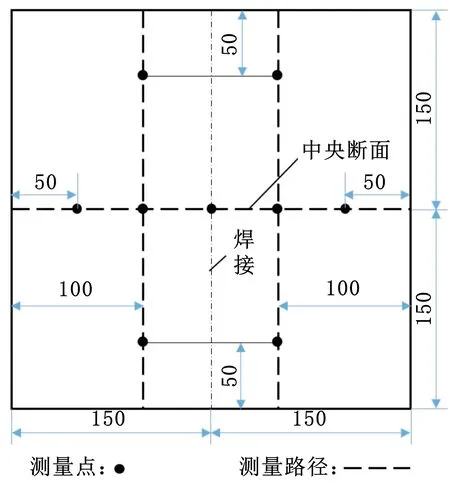
图3 测量位置的分布

热弹塑性有限元计算结果、固有应变法计算结果与沿焊接方向的板横向收缩量分布和角变形量试验值比较结果如图4所示。由图4a可知，热弹塑性计算得到的上表面横向收缩平均值约2.62 mm，试验测量值约2.50 mm；热弹塑性计算得到的下表面横向收缩平均值约1.09 mm，试验测量值约1.15 mm。整体对接接头计算平均值为1.855 mm，而上下表面试验平均值为1.825 mm，误差为2%左右，说明对接接头的横向收缩变形计算结果与试验值吻合良好。另外，固有应变法计算的横向收缩结果为1.72 mm，相比试验平均值，误差为6%左右。由图4b可以看出，热弹塑性计算结果角变形(通过挠度Uz反映)分布趋势与试验测量结果一致；对于中央断面上的最大角变形量，计算结果达到-8.1 mm左右，而试验测量值达到-9.2 mm，误差达12%。另外，固有应变计算最大值达到-8.0 mm，固有应变计算误差为13%。

(a)横向收缩分布

为了更直观地观察两种数值计算的变形结果，图5给出了厚度方向的变形云图，可看出数值结果和固有应变法计算结果吻合较好。

图5 厚度方向的变形云图

2.2 典型接头的固有应变的变化规律

本文以两种典型的异种钢焊接接头，即Q345钢与SUS304钢对接接头和SUS304翼板Q345钢腹板焊接的T型接头为例，采用Q345/SUS304热弹塑性有限元法分别在不同焊接条件(表2)下进行数值试验。计算得到与固有应变相关的参数即纵向收缩力、横向收缩及角变形。

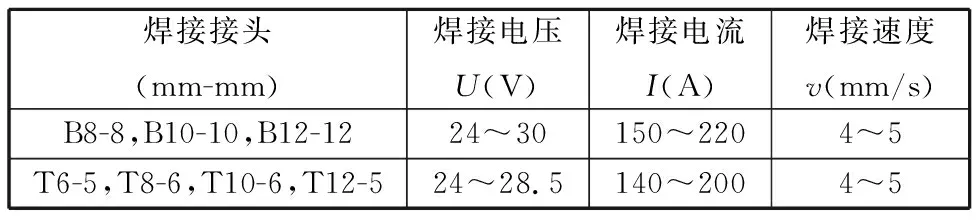
表2 焊接条件

固有变形与焊接热输入参数Q/h2之间存在一定的关系[9]。在表2不同板厚h、不同热输入条件下，计算得到了不同的热输入参数值Q/h2，并与固有应变相关参数即纵向收缩力FT、相对横向收缩S/h、角变形β的关系进行分析，结果如图6所示。

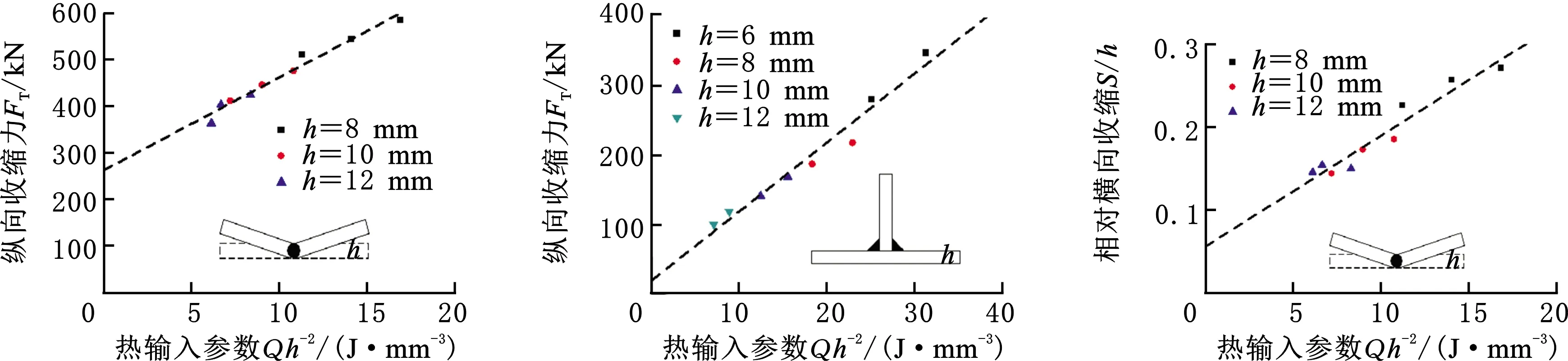
(a)纵向收缩力(对接接头) (b)纵向收缩力(T型接头) (c)相对横向收缩(对接接头)

由图6a、图6c、图6e可知，对于对接接头，在0～20 J/mm3范围内随Q/h2的增大，纵向收缩力和相对横向收缩近似线性增大；而角变形随Q/h2的增大而先增大后减小，并且分界线为Q/h2=12 J/mm3左右。由图6b、图6d、图6f可知，对于T型接头，在0～40 J/mm3范围内随Q/h2的增大，纵向收缩力和相对横向收缩近似线性增大；而角变形随Q/h2的增大而先增大后减小，并且分界线约为Q/h2=12 J/mm3。

由上述变化规律可以推导出多种板厚、热输入、焊接速度的Q345/SUS304异种钢典型焊接接头的固有变形数据，并建立异种钢典型焊接接头固有变形数据库。

3 焊接结构的变形预测

对整体加筋板结构进行完整的热弹塑性计算，得到了结构焊后的变形。与此同时，应用异种钢焊接接头的固有应变的变化规律计算得到固有应变数据，然后通过弹性壳单元法得到结构焊后的变形，将两者变形结果进行比较。

3.1 结构模型

加筋板由SUS304钢与Q345钢对接焊形成，尺寸均为1000 mm×500 mm×9 mm，加强筋材料为Q345钢，尺寸均为1000 mm×120 mm×12 mm，定位尺寸详见图7所示的有限元模型。

图7 加筋板模型及接头形式

SUS304与Q345之间采用MIG焊接，Q345之间焊接采用CO2气体保护焊。焊接顺序为板材对接焊→加强筋点焊固定位置→y方向加强筋角接焊→x方向加强筋角接焊。焊接工艺参数见表3。

表3 焊接工艺参数

3.2 变形计算与结果

根据上文得到的异种钢固有应变的变化规律，并参考单一材料T型焊接固有应变的变化规律[10]，获得加筋板焊接工艺参数下焊接接头的固有应变数据，通过弹性壳单元法按照焊接顺序逐次激活不同的焊道，加载计算得到整体异种钢加筋板结构焊接变形。该计算结果变形云图和热弹塑性法计算的变形云图见图8，可观察到异种钢板经历对接焊，角接焊后出现明显变形。

为定量比较两种计算结果，图9、图10分别给出了加筋板模型中直线1和直线2(图8)的挠度Uz变形曲线。

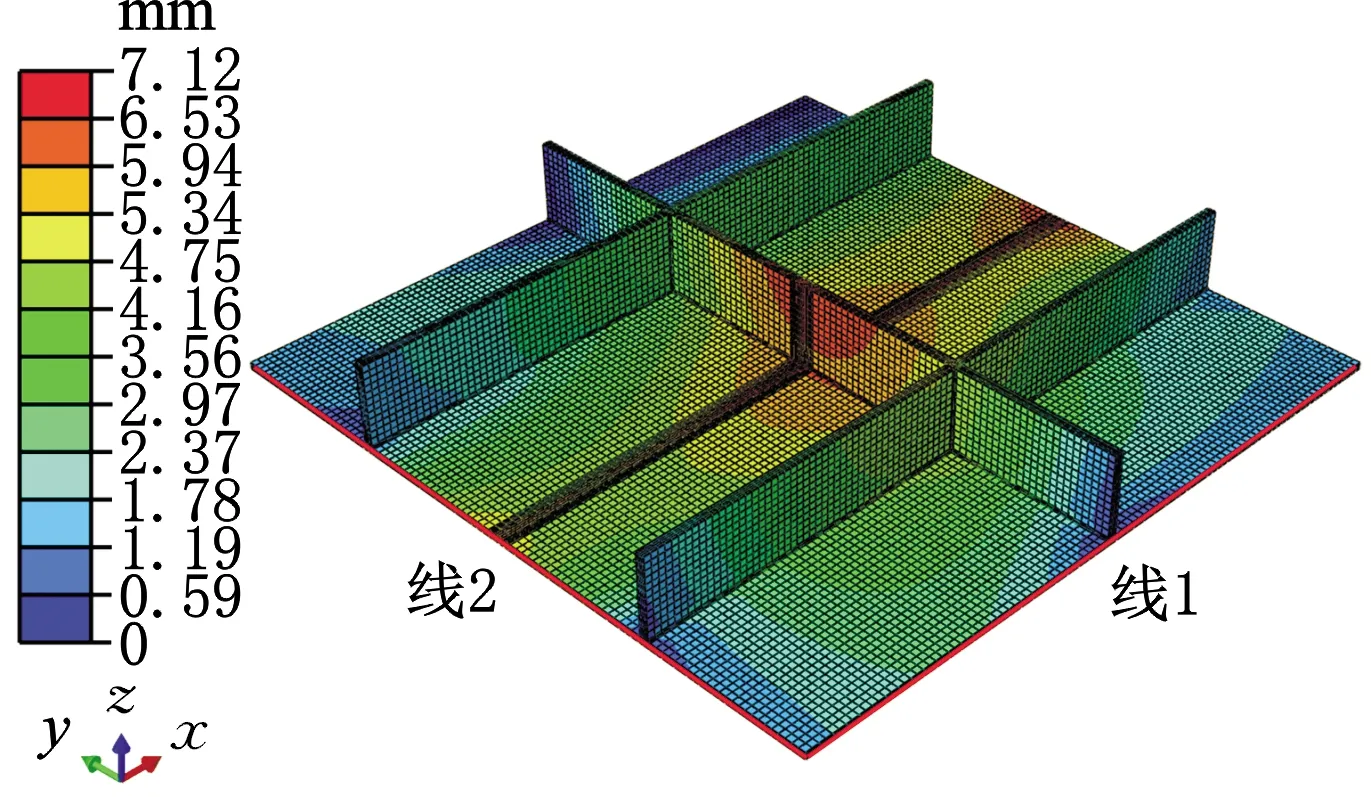
(a)热弹塑性法

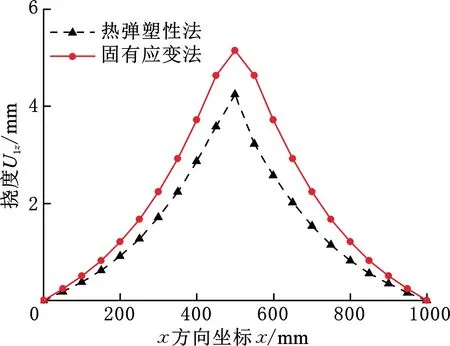
图9 沿线1方向的挠度变形

图10 沿线2方向的挠度变形

由图9可以看出，两种方法的变形结果以x=500 mm为中心基本呈对称分布并沿着两侧下降且趋势较为吻合，热弹塑性法最大挠度值结果为4.2 mm，固有应变法结果为5.0 mm，误差为16%左右。由图10可以看出，两者的变形结果以y=500 mm为中心对称分布，沿着两侧下降，在距离对称点250 mm左右突变下降且趋势一致，热弹塑性有限元法最大挠度值为6.8 mm，固有应变法结果为7.6 mm，误差为10%左右。两者变形分布差距产生的主要原因是热弹塑性法计算过程中焊接时存在板的边缘效应，焊道之间存在相互影响等，而固有应变法忽略了上述因素，仅按照焊道顺序逐次加载弹性计算。综上所述，不论是变形的趋势还是大小，加筋板焊接数值模拟固有应变法与热弹塑性有限元法的计算结果较为吻合，该方法能够准确预测大型异种钢结构焊接变形，也验证了本文固有应变变化规律的可靠性。